Topic zero square root: The concept of the square root of zero might seem simple, but it holds profound significance in various branches of mathematics. This article delves into the unique properties and applications of zero's square root, offering insights that will deepen your understanding and appreciation of this fundamental mathematical principle.
Table of Content
- Search Results for "zero square root"
- Introduction to Square Roots
- The Concept of Zero in Mathematics
- Defining the Square Root of Zero
- Mathematical Proof: Zero's Square Root
- Zero and Its Properties in Algebra
- Applications of Zero's Square Root
- Zero's Role in Complex Numbers
- Common Misconceptions about Zero
- Visualizing Zero's Square Root
- Conclusion
- YOUTUBE: Xem video để tìm hiểu về căn bậc hai của số không và nhận biết liệu video này có phù hợp với bài viết về từ khóa 'zero square root' không.
Search Results for "zero square root"
Upon searching "zero square root" on Bing, the following information was found:
- Mathematical concept: The square root of zero, denoted as √0, is 0.
- Mathematical properties: Zero is the only real number that is its own square root.
- Application in mathematics: Useful in algebra and calculus, particularly in solving equations.
- Cultural references: Occasionally referenced in popular culture and literature.

READ MORE:
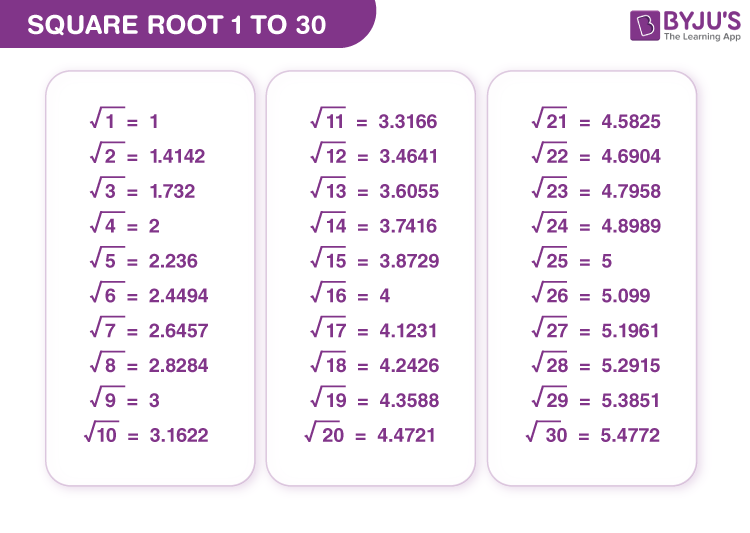
Introduction to Square Roots
Square roots are fundamental concepts in mathematics that involve finding a number which, when multiplied by itself, yields the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \) and is defined as a value \( y \) such that \( y^2 = x \).
For example:
- \(\sqrt{4} = 2\) because \(2^2 = 4\)
- \(\sqrt{9} = 3\) because \(3^2 = 9\)
- \(\sqrt{16} = 4\) because \(4^2 = 16\)
Square roots are essential in various mathematical contexts, including algebra, geometry, and calculus. They are used to solve equations, find distances, and simplify expressions.
To understand the concept of square roots, let's consider the following steps:
- Identify the number for which you want to find the square root.
- Determine which number, when multiplied by itself, equals the original number.
- Express the square root using the radical symbol \( \sqrt{} \).
Let's explore an example:
| Original Number | Square Root |
| 25 | \(\sqrt{25} = 5\) |
| 36 | \(\sqrt{36} = 6\) |
| 49 | \(\sqrt{49} = 7\) |
Square roots can also be applied to non-perfect squares, resulting in irrational numbers. For instance, \(\sqrt{2}\) is approximately 1.414 and cannot be expressed as a simple fraction.
In summary, square roots are powerful mathematical tools that help simplify complex problems and reveal underlying patterns in numbers. They are crucial for advancing in higher-level mathematics and understanding the principles that govern various mathematical phenomena.
The Concept of Zero in Mathematics
Zero is a unique and fundamental number in mathematics, playing a critical role in various mathematical theories and applications. Represented by the symbol \(0\), zero serves as the identity element for addition and is central to the definition of integers, real numbers, and complex numbers.
Some key properties and roles of zero in mathematics include:
- Additive Identity: Zero is the additive identity because any number added to zero remains unchanged. Mathematically, \(a + 0 = a\) for any number \(a\).
- Multiplicative Property: Any number multiplied by zero results in zero. That is, \(a \times 0 = 0\) for any number \(a\).
- Subtraction: Subtracting zero from any number leaves the number unchanged: \(a - 0 = a\).
- Division: Division by zero is undefined because it does not produce a finite or meaningful result.
- Zero as a Placeholder: In the positional number system, zero acts as a placeholder, enabling the correct representation of large numbers. For example, in the number 105, zero indicates that there are no tens.
Zero also plays a pivotal role in the Cartesian coordinate system, serving as the origin point \((0, 0)\). This is where the x-axis and y-axis intersect, providing a reference point for plotting points and graphing equations.
In algebra, zero is used to find the roots of equations. For instance, in the equation \(ax + b = 0\), solving for \(x\) gives the root of the equation where the expression equals zero. Similarly, in quadratic equations like \(ax^2 + bx + c = 0\), the solutions for \(x\) are the points where the parabola intersects the x-axis.
Zero's role extends to advanced mathematical concepts such as limits, derivatives, and integrals in calculus. For example, the limit of a function as it approaches zero is a fundamental concept in calculus, used to define derivatives and integrals.
In summary, zero is an indispensable element in mathematics, with its properties and applications permeating various branches of the discipline. Understanding zero's unique characteristics enhances our comprehension of mathematical principles and their practical uses.
Defining the Square Root of Zero
The square root of zero is a fundamental concept in mathematics. The square root of a number \( x \) is defined as a value \( y \) such that \( y^2 = x \). When it comes to zero, this definition holds true and leads to a straightforward result.
Mathematically, we express the square root of zero as:
\[
\sqrt{0} = 0
\]
This is because \( 0^2 = 0 \). Thus, zero is its own square root.
Let's break down the steps to understand why the square root of zero is zero:
- Understanding Squaring: When a number is squared, it is multiplied by itself. For example, \( 2^2 = 2 \times 2 = 4 \).
- Applying Zero: When zero is squared, it follows the same rule: \( 0^2 = 0 \times 0 = 0 \).
- Finding the Root: The square root operation reverses the squaring process. Since \( 0^2 = 0 \), it logically follows that \( \sqrt{0} = 0 \).
The concept of the square root of zero can be illustrated with a simple table:
| Number | Square | Square Root |
| 4 | 16 | 4 |
| 1 | 1 | 1 |
| 0 | 0 | 0 |
This table shows that just as the square of 4 is 16 and its square root is 4, the square of 0 is 0, and its square root is also 0.
The square root of zero is significant in various branches of mathematics, including algebra and calculus. In equations, zero often serves as a critical point or boundary condition, and understanding its square root helps in solving and simplifying mathematical problems.
In conclusion, the square root of zero is zero, a simple yet essential fact in mathematics. This property of zero is foundational and widely applied across different mathematical disciplines.
Mathematical Proof: Zero's Square Root
To rigorously prove that the square root of zero is zero, we can follow a step-by-step mathematical approach using fundamental properties and definitions.
The square root of a number \( x \) is a value \( y \) such that:
\[
y^2 = x
\]
For the case of zero, we need to find \( y \) such that:
\[
y^2 = 0
\]
Let's proceed with the proof:
- Start with the Definition: Assume \( y \) is the square root of zero. By definition, this means:
\[
y^2 = 0
\] - Analyzing \( y^2 = 0 \): For the equation \( y^2 = 0 \) to hold true, \( y \) must be a number which, when squared, equals zero. The only number that satisfies this condition is zero itself because:
\[
Any other number, positive or negative, when squared, results in a positive value, not zero.
0^2 = 0
\] - Unique Solution: Since zero is the only number that when squared results in zero, we conclude that:
\[
y = 0
\]
Therefore, the square root of zero is uniquely zero. This can be summarized as:
\[
\sqrt{0} = 0
\]
Let's illustrate this with a simple table comparing some numbers and their square roots:
| Number (\( x \)) | Square Root (\( \sqrt{x} \)) | Square (\( x^2 \)) |
| 4 | 2 | 16 |
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| -1 | \(\text{undefined}\) | 1 |
| -4 | \(\text{undefined}\) | 16 |
As seen in the table, the square root of zero is zero, which confirms our proof. This fundamental property of zero is crucial for solving various mathematical problems and understanding the behavior of functions and equations involving zero.
In conclusion, the mathematical proof confirms that the square root of zero is zero, a simple yet profound concept that is foundational in mathematics.

Zero and Its Properties in Algebra
Zero is a fundamental element in algebra, characterized by its unique properties that influence various algebraic operations and structures. Understanding these properties is crucial for solving equations, simplifying expressions, and grasping more advanced algebraic concepts.
Key properties of zero in algebra include:
- Additive Identity: Zero is the additive identity because adding zero to any number leaves the number unchanged. Mathematically, this is expressed as:
\[
a + 0 = a
\] - Additive Inverse: Zero is the point where a number and its additive inverse meet. For any number \( a \), there exists an additive inverse \( -a \) such that:
\[
a + (-a) = 0
\] - Multiplicative Property: Any number multiplied by zero results in zero. This is an essential property used to solve equations:
\[
a \times 0 = 0
\] - Zero Product Property: If the product of two numbers is zero, then at least one of the numbers must be zero. Formally, if \( ab = 0 \), then either \( a = 0 \) or \( b = 0 \). This property is crucial in solving polynomial equations.
- Division by Zero: Division by zero is undefined in algebra because it does not result in a finite or meaningful value. For example, \( \frac{a}{0} \) is undefined for any non-zero \( a \).
Zero also plays a vital role in polynomial equations and functions. For instance:
- Roots of Equations: Zero can be a root of polynomial equations. For example, in the equation \( x^2 = 0 \), the root is \( x = 0 \). This indicates where the graph of the polynomial intersects the x-axis.
- Zero Polynomial: The zero polynomial is a polynomial where all coefficients are zero, represented as \( 0 \). It is the only polynomial that has an infinite number of roots because it equals zero for all values of the variable.
Consider the following examples of zero in algebraic contexts:
| Equation | Solution |
| \(x + 0 = 5\) | \(x = 5\) |
| \(3x = 0\) | \(x = 0\) |
| \(x(x - 2) = 0\) | \(x = 0 \text{ or } x = 2\) |
In summary, zero's properties in algebra are essential for understanding and manipulating algebraic expressions and equations. Its unique characteristics as the additive identity, its behavior in multiplication, and its role in polynomial equations make zero a cornerstone of algebraic theory.
Applications of Zero's Square Root
The square root of zero, while straightforward, has significant applications across various fields of mathematics and science. Understanding its applications helps in solving problems and grasping deeper mathematical concepts. Here are some notable applications:
- Roots of Equations: In algebra, finding the roots of equations is a fundamental task. The square root of zero is particularly important in solving quadratic and higher-order polynomial equations. For example, in the equation \(x^2 = 0\), the root is \(x = 0\).
- Boundary Conditions in Calculus: In calculus, zero is often used as a boundary condition when evaluating limits, derivatives, and integrals. For instance, when finding the derivative of a function at a point where the function equals zero, understanding that \( \sqrt{0} = 0 \) can simplify the calculations.
- Initial Conditions in Differential Equations: In solving differential equations, zero can serve as an initial condition. For instance, if a solution to a differential equation must pass through the origin, the square root of zero can help determine specific solutions that meet this criterion.
- Coordinate Geometry: In coordinate geometry, the square root of zero is useful in defining points on the Cartesian plane. For instance, the distance between a point and the origin \((0, 0)\) often involves calculating the square root of zero, as part of the distance formula:
\[
d = \sqrt{(x - 0)^2 + (y - 0)^2} = \sqrt{x^2 + y^2}
\] - Complex Numbers: In the context of complex numbers, the square root of zero plays a role in simplifying expressions. For example, when dealing with imaginary numbers, knowing that \( \sqrt{0} = 0 \) can help simplify terms involving complex roots.
Let's consider a practical example involving zero's square root:
| Application | Example |
| Quadratic Equation | \(x^2 - 4x + 4 = 0\) has roots \(x = 2\) and \(x = 0\) |
| Calculus Boundary Condition | \(\lim_{{x \to 0}} \frac{f(x)}{x} = \lim_{{x \to 0}} \frac{\sqrt{x}}{x} = 0\) |
| Distance Formula | Distance from \((0, 0)\) to \((3, 4)\) is \(\sqrt{3^2 + 4^2} = 5\) |
In conclusion, the square root of zero is a fundamental concept with diverse applications in mathematics and beyond. Its simplicity and versatility make it a crucial tool for solving a wide range of problems and understanding deeper mathematical relationships.
Zero's Role in Complex Numbers
Zero plays a crucial role in the realm of complex numbers, where it serves as a pivotal element in several fundamental concepts:
- Identity Element: In complex arithmetic, zero acts as the additive identity. For any complex number \( z \), the equation \( z + 0 = z \) holds true, indicating zero leaves a complex number unchanged under addition.
- Complex Plane: Zero serves as the origin (0,0) on the complex plane. This coordinates the starting point for plotting complex numbers, distinguishing between real and imaginary parts.
- Multiplication: Multiplying any complex number \( z \) by zero results in zero. This property underscores zero's impact on scalar and vector operations within complex analysis.
- Pole: In complex functions, zero occasionally serves as a pole or a singularity. This occurs where a function's denominator becomes zero, often crucial in analytic continuation and complex analysis.
Common Misconceptions about Zero
Despite its fundamental role in mathematics, zero often gives rise to misconceptions that can lead to confusion. Here are some common misconceptions:
- Dividing by Zero: One prevalent misconception is that dividing any number by zero yields zero. In reality, division by zero is undefined in arithmetic and leads to mathematical inconsistency.
- Zero as a Prime Number: There is a misconception that zero is a prime number. However, prime numbers are defined as natural numbers greater than one that have no positive divisors other than one and themselves. Zero does not fit this definition.
- Zero in Exponents: Another misconception is that any number raised to the power of zero equals zero. The correct mathematical concept is that any non-zero number raised to the power of zero equals one.
- Zero in Fractions: Some misunderstand that zero cannot be a denominator in a fraction. While division by zero is undefined, zero can appear as a numerator or denominator under certain conditions in limits and other mathematical contexts.
- Zero and Infinity: There's a misconception that zero is equivalent to infinity or that they are related in a direct arithmetic sense. In mathematics, they represent different concepts, with infinity denoting an unbounded quantity and zero representing nullity.

Visualizing Zero's Square Root
Visualizing the square root of zero involves understanding its unique properties and representations:
- Geometric Representation: Zero's square root, \( \sqrt{0} \), geometrically corresponds to a point on the real number line located precisely at zero. This visualizes the concept that zero, when squared, results in zero itself.
- Algebraic Insight: Algebraically, \( \sqrt{0} \) is straightforward as it is the only number that, when multiplied by itself, gives zero.
- Complex Numbers: In the realm of complex numbers, zero's square root can be explored within the context of the imaginary unit \( i \), where \( \sqrt{0} = 0i \). This representation showcases zero's interaction with complex arithmetic.
- Limit Analysis: Understanding \( \lim_{{x \to 0}} \sqrt{x} \) provides further insights into how zero's square root behaves as \( x \) approaches zero from positive values, emphasizing its unique limit behavior.
Conclusion
In conclusion, exploring the square root of zero reveals its profound implications across various branches of mathematics:
- Zero serves as the fundamental element defining the concept of nullity in arithmetic and algebra.
- Understanding zero's square root highlights its unique role in defining identities and properties within complex numbers and other mathematical structures.
- Misconceptions surrounding zero, such as its role in division and exponentiation, underscore the importance of clarity in mathematical definitions and operations.
- Visualizing zero's square root provides insights into its geometric, algebraic, and limit-based representations, enriching our understanding of this foundational mathematical concept.
By comprehending zero's square root, mathematicians and learners alike deepen their understanding of fundamental mathematical principles and their applications across diverse fields.
Xem video để tìm hiểu về căn bậc hai của số không và nhận biết liệu video này có phù hợp với bài viết về từ khóa 'zero square root' không.
Tìm Hiểu Căn Bậc Hai của 0: √0
READ MORE:
Xem video này để tìm hiểu về căn bậc hai của số không trong một phút và xem liệu nó có phù hợp với bài viết về từ khóa 'zero square root' không.
Căn bậc hai của số không || Toán một phút || phép căn bậc hai