Topic 8 square root of 3: Welcome to our comprehensive guide on the 8 square root of 3. In this article, we will simplify and explore the mathematical concept, providing step-by-step solutions, practical applications, and advanced calculations to help you master square roots with ease.
Table of Content
- Mathematical Expression: 8√3
- Introduction to Square Roots
- Mathematical Definition of Square Roots
- How to Simplify Square Roots
- Examples of Simplifying Square Roots
- Step-by-Step Solution: Simplify 8√3
- Using Calculators for Square Root Problems
- Common Applications of Square Roots
- Advanced Square Root Calculations
- Practical Tips for Estimating Square Roots
- YOUTUBE: Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai để giúp bạn nắm vững kiến thức và làm bài tập toán dễ dàng hơn.
Mathematical Expression: 8√3
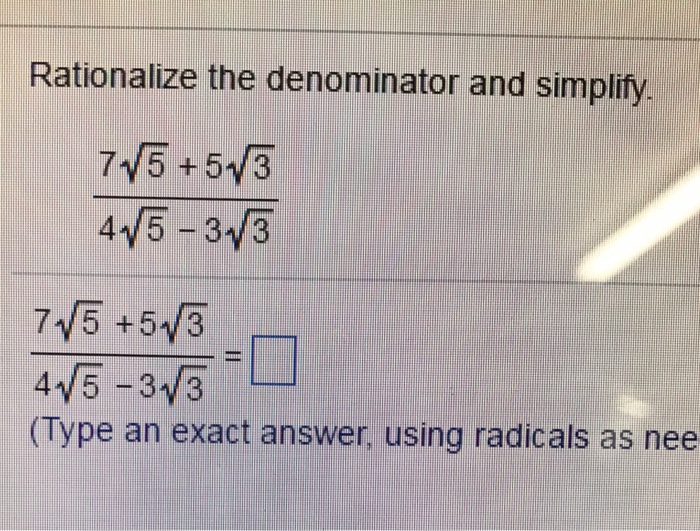
The expression \( 8\sqrt{3} \) involves the multiplication of 8 by the square root of 3. This is a common expression in algebra and can be represented in various forms, including exact and decimal forms.
Exact Form
In its exact form, the expression remains as \( 8\sqrt{3} \). This representation is often used in algebraic manipulations and theoretical work.
Decimal Form
When calculated, the decimal form of \( 8\sqrt{3} \) is approximately 13.856. This form is useful for practical calculations where an approximate numerical value is required.
Properties
- \( \sqrt{3} \) is an irrational number, meaning it cannot be expressed as a simple fraction.
- The value of \( \sqrt{3} \) is approximately 1.732.
- Multiplying 8 by 1.732 gives approximately 13.856.
Applications
The expression \( 8\sqrt{3} \) appears in various mathematical contexts, such as geometry, where it might be used to calculate lengths in triangles, or in physics, where it could represent certain quantities in equations involving square roots.
| Expression | Exact Form | Decimal Form |
|---|---|---|
| \( 8\sqrt{3} \) | 8√3 | 13.856 |
Calculation Steps
- Identify the value of the square root of 3: \( \sqrt{3} \approx 1.732 \).
- Multiply this value by 8: \( 8 \times 1.732 \approx 13.856 \).
Using various online calculators and tools, such as those provided by Mathway, Symbolab, and Calculator.net, you can easily compute and verify these values.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, yields the original number. For instance, the square root of 9 is 3, as \(3 \times 3 = 9\). Understanding square roots is crucial for solving various mathematical problems, from basic arithmetic to advanced calculus.
Key properties of square roots include:
- Non-negative results: Square roots of non-negative numbers are always non-negative. For example, the square root of 16 is 4.
- Radical notation: The square root of a number \(a\) is denoted as \(\sqrt{a}\).
- Perfect squares: Numbers like 1, 4, 9, 16, etc., whose square roots are integers.
In this article, we will explore how to simplify and calculate the square root of 3, specifically focusing on simplifying expressions like \(8\sqrt{3}\).
Mathematical Definition of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, if \( x \) is the square root of \( y \), then \( x^2 = y \). The square root symbol is denoted as \( \sqrt{} \). For example, the square root of 16 is written as \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
The concept of square roots can be understood through several key properties:
- Non-negative Principal Root: The principal square root of a non-negative number is non-negative. For example, \( \sqrt{25} = 5 \), not -5.
- Imaginary Numbers: The square root of a negative number involves imaginary numbers, denoted as \( i \). For example, \( \sqrt{-1} = i \).
- Radical Expressions: A square root can be part of a more complex expression, such as \( 8\sqrt{3} \), which simplifies calculations involving irrational numbers.
Square roots play a vital role in various branches of mathematics, including algebra, geometry, and calculus. They are used to solve equations, calculate distances, and analyze patterns.
For example, simplifying \( 8\sqrt{3} \) involves recognizing that \( 8 \) is a coefficient and \( \sqrt{3} \) is an irrational number. This expression represents a value approximately equal to \( 8 \times 1.732 \), which simplifies to roughly 13.856.
How to Simplify Square Roots
Simplifying square roots involves expressing the square root in its simplest form. Here are the steps to simplify square roots:
- Identify Perfect Squares: Find any perfect square factors of the number under the square root. Perfect squares are numbers like 1, 4, 9, 16, 25, etc.
- Factorize the Number: Break down the number under the square root into its prime factors and identify pairs of prime factors. For example, for \( \sqrt{72} \), the factorization is \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Extract the Perfect Squares: Move pairs of factors outside the square root. Each pair of identical factors becomes a single factor outside the radical. Using the previous example, \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
- Simplify the Expression: Multiply the factors outside the square root to get the final simplified form. Continuing the example, \( 6\sqrt{2} \) is the simplified form of \( \sqrt{72} \).
Let's apply these steps to simplify \( 8\sqrt{3} \):
- The number 3 is already a prime number, and 8 is a coefficient outside the square root.
- Since there are no perfect square factors in 3, the expression \( \sqrt{3} \) cannot be simplified further.
- The expression \( 8\sqrt{3} \) is already in its simplest form.
Thus, \( 8\sqrt{3} \) remains \( 8\sqrt{3} \) as there are no further simplifications possible.
Examples of Simplifying Square Roots
Here are several examples to illustrate the process of simplifying square roots:
Example 1: Simplifying \( \sqrt{50} \)
- Identify Perfect Squares: The number 50 can be factored into \( 25 \times 2 \), where 25 is a perfect square.
- Factorize the Number: \( \sqrt{50} = \sqrt{25 \times 2} \).
- Extract the Perfect Squares: Move the factor 25 outside the square root: \( \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} \).
- Simplify the Expression: Since \( \sqrt{25} = 5 \), the expression simplifies to \( 5\sqrt{2} \).
So, \( \sqrt{50} = 5\sqrt{2} \).
Example 2: Simplifying \( \sqrt{72} \)
- Identify Perfect Squares: The number 72 can be factored into \( 36 \times 2 \), where 36 is a perfect square.
- Factorize the Number: \( \sqrt{72} = \sqrt{36 \times 2} \).
- Extract the Perfect Squares: Move the factor 36 outside the square root: \( \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} \).
- Simplify the Expression: Since \( \sqrt{36} = 6 \), the expression simplifies to \( 6\sqrt{2} \).
So, \( \sqrt{72} = 6\sqrt{2} \).
Example 3: Simplifying \( 8\sqrt{3} \)
As discussed earlier, \( 8\sqrt{3} \) is already in its simplest form because 3 is a prime number and there are no perfect square factors to extract. Therefore, \( 8\sqrt{3} \) remains \( 8\sqrt{3} \).
Example 4: Simplifying \( \sqrt{200} \)
- Identify Perfect Squares: The number 200 can be factored into \( 100 \times 2 \), where 100 is a perfect square.
- Factorize the Number: \( \sqrt{200} = \sqrt{100 \times 2} \).
- Extract the Perfect Squares: Move the factor 100 outside the square root: \( \sqrt{100 \times 2} = \sqrt{100} \times \sqrt{2} \).
- Simplify the Expression: Since \( \sqrt{100} = 10 \), the expression simplifies to \( 10\sqrt{2} \).
So, \( \sqrt{200} = 10\sqrt{2} \).

Step-by-Step Solution: Simplify 8√3
Simplifying the expression \( 8\sqrt{3} \) involves understanding the components of the expression and ensuring it is in its simplest form. Here are the steps to simplify \( 8\sqrt{3} \):
- Identify the Coefficient and Radical: In \( 8\sqrt{3} \), the number 8 is the coefficient, and \( \sqrt{3} \) is the radical part.
- Check for Perfect Squares: Determine if the number under the square root (3) has any perfect square factors. Since 3 is a prime number, it does not have any perfect square factors other than 1.
- Simplify the Radical: Since \( \sqrt{3} \) cannot be simplified further, we focus on the coefficient. The expression remains \( 8\sqrt{3} \) because the radical part is already in its simplest form.
Thus, the simplified form of \( 8\sqrt{3} \) is:
\( 8\sqrt{3} \)
Here's a step-by-step breakdown in a tabular format for clarity:
| Step | Action | Result |
|---|---|---|
| 1 | Identify the coefficient and radical | \( 8 \) and \( \sqrt{3} \) |
| 2 | Check for perfect squares in the radical | No perfect squares other than 1 |
| 3 | Simplify the radical (if possible) | \( \sqrt{3} \) (already simplified) |
| 4 | Combine the simplified parts | \( 8\sqrt{3} \) |
Therefore, the expression \( 8\sqrt{3} \) is already in its simplest form.
Using Calculators for Square Root Problems
Calculators are invaluable tools for solving square root problems, especially when dealing with complex or large numbers. Here is a step-by-step guide on how to use calculators for square root problems:
- Basic Square Root Calculation:
- Turn on the calculator and locate the square root (√) button.
- Input the number for which you need the square root. For example, to find \( \sqrt{3} \), press the number 3.
- Press the square root (√) button to get the result. The display should show approximately 1.732.
- Calculating Expressions Involving Square Roots:
- For expressions like \( 8\sqrt{3} \), first find the square root of 3 as described above.
- Multiply the result by the coefficient (in this case, 8).
- Example: \( 8 \times 1.732 \approx 13.856 \).
- Enter 8, then multiply by the result of \( \sqrt{3} \) to get the final value.
- Using Scientific Calculators:
- Scientific calculators often have more functions and can handle more complex expressions directly.
- To compute \( 8\sqrt{3} \) on a scientific calculator, you can typically enter the entire expression at once.
- Example: Enter 8, then the multiplication sign (×), followed by the square root function (√), and finally the number 3.
- Press the equals (=) button to get the result, which should be approximately 13.856.
- Online Calculators:
- Online calculators and calculator apps are also useful and often user-friendly.
- Navigate to a reliable online calculator.
- Enter the expression \( 8\sqrt{3} \) directly into the input field and click the calculate button.
- The online tool will display the result, approximately 13.856.
Using calculators simplifies the process of solving square root problems, ensuring accuracy and saving time. Whether using a physical scientific calculator or an online tool, these devices can handle both basic and complex square root calculations with ease.
Common Applications of Square Roots
Square roots are fundamental in various fields and have numerous practical applications. Below are some common areas where square roots play a crucial role:
- Geometry:
In geometry, square roots are used to determine the lengths of sides in right triangles using the Pythagorean theorem. For example, if a right triangle has legs of length 3 and 4, the hypotenuse can be found using the formula:
\[
c = \sqrt{a^2 + b^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] - Physics:
Square roots are used in physics to solve problems related to motion and energy. For instance, the formula for the period of a simple pendulum is given by:
\[
T = 2\pi \sqrt{\frac{L}{g}}
\]where \( T \) is the period, \( L \) is the length of the pendulum, and \( g \) is the acceleration due to gravity.
- Engineering:
Engineers use square roots in various calculations, including determining the natural frequencies of structures and in stress analysis. For example, the natural frequency of a beam can be calculated as:
\[
f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\]where \( f \) is the frequency, \( k \) is the stiffness of the beam, and \( m \) is the mass.
- Finance:
In finance, square roots are used in the calculation of standard deviation and variance, which are measures of volatility and risk. The formula for standard deviation is:
\[
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}
\]where \( \sigma \) is the standard deviation, \( N \) is the number of data points, \( x_i \) represents each data point, and \( \mu \) is the mean of the data.
- Computer Science:
In computer graphics, square roots are often used to calculate distances between points in 2D or 3D space. For example, the Euclidean distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\] - Medicine:
Square roots are used in medical research and statistics to analyze data and calculate important metrics such as the root mean square error (RMSE), which helps in assessing the accuracy of predictive models:
\[
\text{RMSE} = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y_i})^2}
\]where \( N \) is the number of observations, \( y_i \) is the observed value, and \( \hat{y_i} \) is the predicted value.
Advanced Square Root Calculations
Advanced square root calculations often involve more complex techniques and applications. Here, we explore some sophisticated methods and concepts.
Iterative Methods for Approximating Square Roots
For non-perfect squares, advanced iterative methods can be used to find square roots to a high degree of accuracy. One common method is Newton's method (also known as the Newton-Raphson method).
- Initial Guess: Start with an initial guess \( x_0 \). A reasonable guess can be \( x_0 = \frac{a}{2} \) where \( a \) is the number whose square root we want to find.
- Iteration Formula: Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{a}{x_n} \right) \) to generate a better approximation.
- Repeat: Repeat the iteration until the difference between successive approximations is less than the desired tolerance.
Example: To find \( \sqrt{8} \) using Newton's method:
- Initial guess: \( x_0 = 4 \)
- Iteration 1: \( x_1 = \frac{1}{2} \left( 4 + \frac{8}{4} \right) = 3 \)
- Iteration 2: \( x_2 = \frac{1}{2} \left( 3 + \frac{8}{3} \right) \approx 2.833 \)
- Continue iterating until desired accuracy is achieved.
Properties and Applications
Square roots have important properties and applications in various fields:
- Multiplying and Dividing Square Roots:
- \( \sqrt{a} \times \sqrt{b} = \sqrt{a \times b} \)
- \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \)
- Adding and Subtracting Square Roots: Unlike multiplication and division, addition and subtraction of square roots do not have straightforward simplifications unless the terms are like terms:
- \( m\sqrt{a} + n\sqrt{a} = (m+n)\sqrt{a} \)
- \( m\sqrt{a} - n\sqrt{a} = (m-n)\sqrt{a} \)
Rationalizing the Denominator
When a square root appears in the denominator of a fraction, we can rationalize it by multiplying both the numerator and the denominator by the square root. For example:
\( \frac{5}{\sqrt{3}} = \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5\sqrt{3}}{3} \)
Complex Square Roots
Square roots of negative numbers involve complex numbers. The imaginary unit \( i \) is defined as \( i = \sqrt{-1} \). Thus, for any negative number \( -a \), the square root can be expressed as:
\( \sqrt{-a} = \sqrt{a} \cdot i \)
Applications in Various Fields
Square roots are used in numerous fields such as:
- Geometry: Calculating distances using the Pythagorean theorem: \( c = \sqrt{a^2 + b^2} \).
- Quadratic Equations: Solving equations of the form \( ax^2 + bx + c = 0 \) using the quadratic formula: \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
- Physics: Determining physical quantities such as root-mean-square speed in kinetic theory of gases.
- Statistics: Standard deviation and variance calculations involve square roots.
Understanding and mastering advanced square root calculations is essential for tackling a wide range of mathematical problems and applications in science and engineering.
Practical Tips for Estimating Square Roots
Estimating square roots can be a valuable skill, especially when an exact calculation is not necessary. Here are some practical tips for estimating square roots effectively:
1. Memorize Perfect Squares
Knowing the perfect squares up to at least \(12^2 = 144\) can help you quickly estimate square roots. For example:
- \(1^2 = 1\)
- \(2^2 = 4\)
- \(3^2 = 9\)
- \(4^2 = 16\)
- \(5^2 = 25\)
- \(6^2 = 36\)
- \(7^2 = 49\)
- \(8^2 = 64\)
- \(9^2 = 81\)
- \(10^2 = 100\)
- \(11^2 = 121\)
- \(12^2 = 144\)
2. Use the "Sandwich" Method
To estimate a square root, find the two perfect squares it lies between. For example, to estimate \(\sqrt{20}\):
- \(16 < 20 < 25\) (since \(4^2 = 16\) and \(5^2 = 25\))
- Therefore, \(4 < \sqrt{20} < 5\)
3. Refine Your Estimate
Once you have narrowed down the range, you can use a more precise method to refine your estimate. Here are two methods:
Guess and Check Method
- Guess a value between the two square roots. For \(\sqrt{20}\), guess 4.5:
- Calculate \(4.5^2 = 20.25\). Since 20.25 is very close to 20, \(\sqrt{20}\) is approximately 4.5.
Averaging Method
- Guess a value, say 4.5.
- Divide the original number by your guess: \(20 / 4.5 \approx 4.44\).
- Average the guess and the result: \((4.5 + 4.44) / 2 \approx 4.47\).
- Repeat the process until the result converges: \(20 / 4.47 \approx 4.48\), and average again \((4.47 + 4.48) / 2 \approx 4.475\).
4. Use Fractions for Non-Integers
When dealing with non-integer square roots, convert the number into a fraction. For example, to estimate \(\sqrt{1.5}\):
- Convert 1.5 to a fraction: \(1.5 = \frac{3}{2}\).
- Estimate \(\sqrt{\frac{3}{2}} = \frac{\sqrt{3}}{\sqrt{2}} \approx \frac{1.73}{1.41} \approx 1.22\).
5. Practice with Common Roots
Memorize common square roots for quicker estimation:
- \(\sqrt{2} \approx 1.414\)
- \(\sqrt{3} \approx 1.732\)
- \(\sqrt{5} \approx 2.236\)
6. Use a Calculator for Precision
While these methods are helpful for quick estimates, use a calculator for precise calculations when needed.
READ MORE:
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai để giúp bạn nắm vững kiến thức và làm bài tập toán dễ dàng hơn.
Cách Đơn Giản Hóa Căn Bậc Hai