Topic square root 8 simplified: The square root of 8 simplified is a common mathematical problem. The simplified form of the square root of 8 is \(2\sqrt{2}\). This simplification helps in various mathematical calculations and is a useful piece of knowledge for students and math enthusiasts. Let's explore how to simplify the square root of 8 and understand its significance in mathematics.
Table of Content
- Square Root of 8 Simplified
- Introduction
- Understanding Square Roots
- Definition and Properties
- Methods to Simplify the Square Root of 8
- Prime Factorization Method
- Long Division Method
- Examples and Applications
- Calculating the Square Root of 8
- Conclusion
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai của số 8 (sqrt(8)) một cách dễ hiểu và chi tiết. Thích hợp cho người mới học toán.
Square Root of 8 Simplified
The square root of 8 can be simplified to its simplest radical form. Below are the steps and important details:
Important Facts
- The square root of 8 is represented as √8.
- In simplest radical form, √8 is 2√2.
- The decimal value of √8 is approximately 2.828.
- Since 8 is not a perfect square, its square root is an irrational number.
Simplification Steps
- Factorize 8 into its prime factors: 8 = 2 × 4 = 2 × 2 × 2.
- Group the factors into pairs: 8 = 2² × 2.
- Take the square root of each pair: √(2² × 2) = 2√2.
Thus, the simplified form of √8 is 2√2.
Value Calculation
To find the approximate decimal value of √8:
- We know √2 is approximately 1.414.
- Therefore, 2√2 ≈ 2 × 1.414 = 2.828.
Applications and Examples
Here are some practical examples where the square root of 8 is used:
- Finding the side length of a square with an area of 8 square units. The side length is √8 = 2√2 units.
- Determining the height of a structure with an area of 8 square units in specific contexts like construction or design.
FAQs
- What is the simplest form of the square root of 8? The simplest form is 2√2.
- Is the square root of 8 rational? No, it is irrational.
- What is the approximate decimal value of the square root of 8? It is approximately 2.828.

READ MORE:
Introduction
The square root of 8 can be simplified to its simplest radical form, which is 2√2. This simplification is an essential concept in algebra, making it easier to work with the value in various mathematical contexts. In this section, we will explore the method to simplify the square root of 8 and understand its properties and applications.
To begin, we recognize that the number 8 can be expressed as a product of its prime factors: 8 = 4 × 2. Since 4 is a perfect square, we can simplify the square root as follows:
- Express 8 as a product of 4 and 2: 8 = 4 × 2.
- Take the square root of both sides: √8 = √(4 × 2).
- Separate the square root into two parts: √8 = √4 × √2.
- Simplify the square root of 4, which is 2: √8 = 2 × √2.
Thus, the simplified form of √8 is 2√2.
Understanding this simplification is crucial for solving more complex problems involving square roots. The value of √8, approximately 2.828, is an irrational number, meaning it cannot be expressed as a simple fraction. This makes 2√2 a quadratic surd, a term used to describe square roots of numbers that are not perfect squares.
In mathematical practice, simplifying square roots helps in various calculations, such as solving quadratic equations, integrating functions, and working with geometric properties. The simplified form 2√2 is not only easier to work with but also provides a clearer understanding of the value's relationship to other numbers.
Understanding Square Roots
The concept of square roots is fundamental in mathematics. The square root of a number is a value that, when multiplied by itself, gives the original number. The symbol for square root is '√', and the number under the square root symbol is called the radicand. For example, the square root of 9 is 3, because 3 multiplied by 3 equals 9.
Simplifying square roots involves expressing the radicand as a product of perfect squares. For instance, to simplify the square root of 8, we find that 8 can be factored into 4 and 2, where 4 is a perfect square. Thus, we can write:
\[
\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2}
\]
This process is useful for simplifying more complex square roots and for performing operations involving square roots. Understanding this concept can help solve various mathematical problems and enhance comprehension of algebraic principles.
- Identify the radicand.
- Factorize the radicand into its prime factors.
- Group the factors into pairs of perfect squares.
- Simplify the expression by taking the square root of the perfect squares.
For example, consider the square root of 8. By prime factorization, we get:
\[
8 = 2 \times 2 \times 2
\]
Grouping the factors, we have:
\[
8 = (2 \times 2) \times 2 = 4 \times 2
\]
Therefore, the square root of 8 is simplified as:
\[
\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2}
\]
This method of simplification is essential for solving problems in algebra, geometry, and calculus. It helps in performing arithmetic operations on roots and understanding the properties of numbers more deeply.
Definition and Properties
The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 8, its square root can be represented in both decimal and radical forms. Understanding the properties of the square root of 8 involves simplifying it, exploring its irrational nature, and understanding its representation in mathematical expressions.
- The square root of 8 is denoted as √8.
- In simplest radical form, √8 can be expressed as 2√2.
- The decimal approximation of √8 is 2.828.
- Since 8 is not a perfect square, √8 is an irrational number.
- In exponential form, the square root of 8 is written as 81/2.
To further illustrate these properties, let's consider some calculations:
| Expression | Result |
| √8 | 2√2 |
| Decimal Form | 2.828 |
| 81/2 | 2.828 |
Breaking down the calculation, we get:
- Prime factorize 8: 8 = 2 × 2 × 2.
- Express 8 as a product of squares: 8 = 4 × 2, where 4 is a perfect square.
- Apply the square root to each factor: √8 = √(4 × 2) = √4 × √2 = 2√2.
These steps show the systematic approach to simplifying the square root of 8, demonstrating its properties as both a radical and an irrational number.
Methods to Simplify the Square Root of 8
Simplifying the square root of 8 involves breaking it down into a more manageable form using different mathematical methods. Here, we will explore two main methods: Prime Factorization and Long Division.
Prime Factorization Method
Prime factorization involves expressing the number inside the square root as a product of prime numbers. Let's simplify the square root of 8 using this method:
- Identify the prime factors of 8. We know that \(8 = 2 \times 2 \times 2\).
- Rewrite the expression using these factors under the square root: \(\sqrt{8} = \sqrt{2 \times 2 \times 2}\).
- Group the factors into pairs: \(\sqrt{2^2 \times 2}\).
- Take the square root of the pair of 2s: \(2\). This gives us \(2 \times \sqrt{2}\).
- Thus, the simplified form is \(2 \sqrt{2}\).
Using prime factorization, we find that \( \sqrt{8} = 2 \sqrt{2} \).
Long Division Method
The long division method helps to find the square root by approximating the value step-by-step. Here's how to simplify the square root of 8 using this method:
- Start by setting up 8 as the number whose square root you want to find. You can group the digits in pairs from the decimal point, though here we only have a single digit.
- Find the largest integer whose square is less than or equal to 8. The largest integer is 2, because \(2^2 = 4\), which is less than 8.
- Subtract 4 from 8 to get the remainder 4. Write 2 as the first digit of the square root result.
- Bring down pairs of zeros to the remainder (400) and double the quotient obtained so far (2) to get 4.
- Determine the largest digit \(x\) such that \(4x \times x\) is less than or equal to 400. Here, \(47 \times 7 = 329\), which is less than 400.
- Subtract 329 from 400 to get 71, bring down more zeros, and continue the process to get a more precise value.
- This method can continue indefinitely, but typically we stop after a few decimal places. For practical purposes, we can approximate \( \sqrt{8} \approx 2.828 \).
The long division method gives us a more precise decimal approximation of the square root of 8.
Summary
Both methods help us understand and simplify the square root of 8 in different ways. Prime factorization gives a simplified radical form as \(2 \sqrt{2}\), while the long division method provides a precise decimal approximation as \(2.828\). Depending on the context, either method can be useful for simplifying square roots.
Prime Factorization Method
The prime factorization method is a systematic approach to simplify the square root of a number. Here, we'll apply this method to simplify the square root of 8.
Follow these steps:
-
Find the prime factors of 8:
8 can be factored into 2 × 2 × 2.
We can write this as:
\[ 8 = 2^3 \]
-
Express the square root of 8 using its prime factors:
\[ \sqrt{8} = \sqrt{2^3} \]
-
Rewrite the expression by separating the factors under the square root:
\[ \sqrt{2^3} = \sqrt{2^2 \times 2} \]
-
Use the property of square roots to separate the terms:
\[ \sqrt{2^2 \times 2} = \sqrt{2^2} \times \sqrt{2} \]
-
Simplify the square root of the perfect square:
\[ \sqrt{2^2} = 2 \]
-
Combine the simplified terms:
\[ 2 \times \sqrt{2} \]
Therefore, the simplified form of the square root of 8 is:
\[ \sqrt{8} = 2\sqrt{2} \]
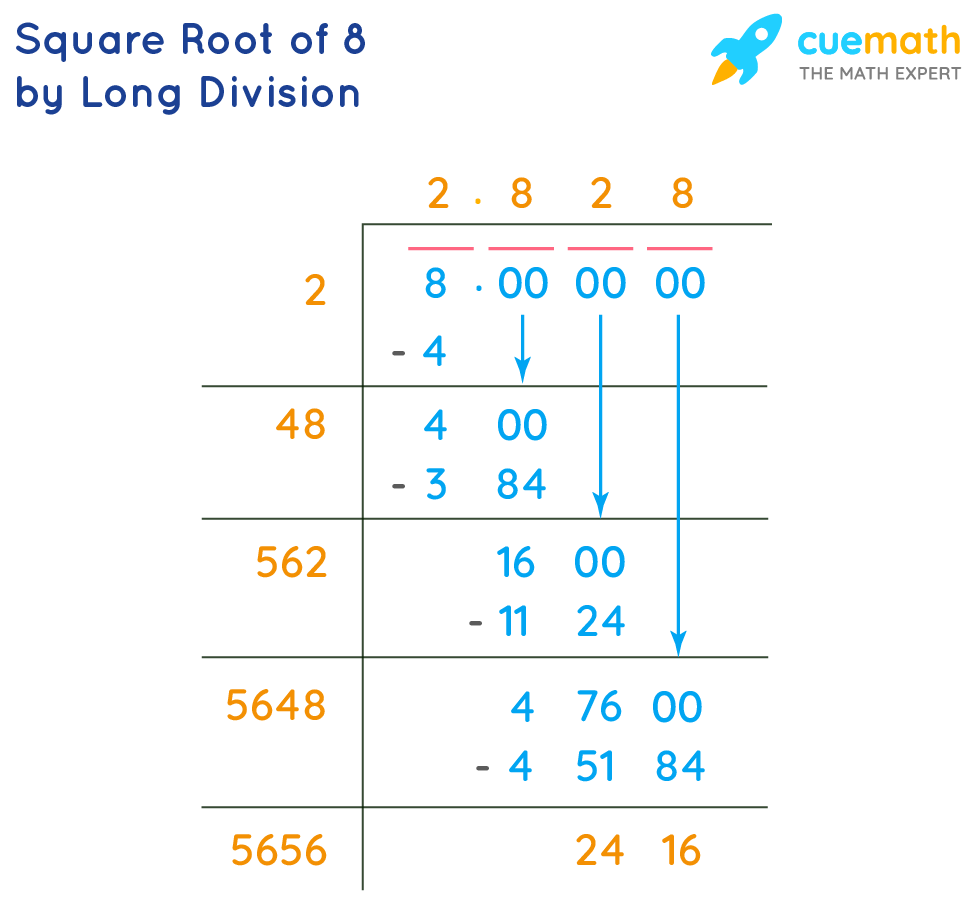
Long Division Method
The long division method is a systematic way to find the square root of a number. Here, we'll apply it to find the square root of 8. Follow these steps:
Start by writing 8 as a number under the division bar.
Pair the digits of 8 starting from the decimal point. Since 8 is a single digit, pair it with a decimal and add pairs of zeros (e.g., 8.00).
Find the largest number whose square is less than or equal to 8. This number is 2, as \(2^2 = 4\).
Write 2 as the divisor and the quotient. Subtract 4 from 8 to get the remainder 4.
Bring down the next pair of zeros to get 400. Double the quotient (2) to get 4 and place it as the new divisor's first digit (e.g., 4_).
Find a digit (x) such that \(4x \times x\) is less than or equal to 400. The correct digit is 6, as \(46 \times 6 = 276\).
Write 6 next to 2 in the quotient, making it 2.6. Subtract 276 from 400 to get the remainder 124.
Bring down another pair of zeros to get 12400. Double the current quotient (2.6 becomes 5.2) and repeat the process.
Continue this process to get more decimal places as needed. The next steps would be finding the digit that when multiplied with the new divisor formed by the doubled quotient gives the closest number less than or equal to the current remainder and brought down zeros.
By continuing the process, the value of the square root of 8 is approximately 2.82842 when rounded to five decimal places.
This method ensures accuracy and helps in understanding the concept of finding square roots manually.
Examples and Applications
The square root of 8 has various examples and applications in real-life situations. Here, we will explore a few examples to understand its practical use:
Example 1: Area of a Square Garden
Mr. Smith wants to fence his square garden, which has an area of 8 square feet. To find the length of each side of the garden, we need to find the square root of 8.
The area of the square (A) = side²
Given, A = 8 square feet
So, side = √8 = 2√2 feet
Hence, each side of the garden is 2√2 feet long.
Example 2: Diagonal of a Square
If a square has sides of length 2√2, what is the length of the diagonal?
Using the Pythagorean theorem, the diagonal (d) of a square with side length (s) is given by:
\( d = \sqrt{s^2 + s^2} = \sqrt{2s^2} = s\sqrt{2} \)
For side \( s = 2\sqrt{2} \):
\( d = 2\sqrt{2} \times \sqrt{2} = 2 \times 2 = 4 \)
Therefore, the diagonal of the square is 4 feet.
Example 3: Length of a Diagonal in a Cube
Consider a cube with each side of length 2. To find the length of the diagonal of this cube:
The diagonal (D) of the cube is given by:
\( D = \sqrt{a^2 + a^2 + a^2} = \sqrt{3a^2} = a\sqrt{3} \)
For side \( a = 2 \):
\( D = 2\sqrt{3} \approx 2 \times 1.732 = 3.464 \)
Thus, the length of the diagonal of the cube is approximately 3.464 units.
Applications in Geometry and Construction
- Geometric Design: The square root of 8 is often used in geometric designs and constructions, especially when dealing with squares and rectangles where precise measurements are crucial.
- Engineering and Architecture: Calculations involving the square root of 8 can be useful in determining dimensions and areas, which are fundamental in engineering and architectural design.
- Mathematical Problem Solving: Simplified square roots are frequently used to solve mathematical problems, making it easier to handle and simplify complex equations.
Example 4: Distance Between Points
In a coordinate plane, the distance between points (0,0) and (2,2√2) can be found using the distance formula:
\( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
For points (0,0) and (2,2√2):
\( d = \sqrt{(2 - 0)^2 + (2\sqrt{2} - 0)^2} = \sqrt{4 + 8} = \sqrt{12} = 2\sqrt{3} \)
The distance between the points is 2√3 units.
Calculating the Square Root of 8
To calculate the square root of 8, we can use several methods. Below, we'll explore the process of simplifying it to its simplest radical form and finding its decimal approximation.
Simplifying to Simplest Radical Form
- Start with the number 8.
- Perform prime factorization: \( 8 = 2 \times 2 \times 2 \).
- Express under the square root: \( \sqrt{8} = \sqrt{2 \times 2 \times 2} \).
- Group the factors in pairs and pull out the pairs from the radical: \[ \sqrt{8} = \sqrt{2^2 \times 2} = 2\sqrt{2} \]
Thus, the simplified radical form of \( \sqrt{8} \) is \( 2\sqrt{2} \).
Decimal Approximation
To find the decimal value, you can use a calculator or perform long division. The square root of 2 is approximately 1.414. Therefore:
\[
2 \times 1.414 = 2.828
\]
So, the decimal approximation of \( \sqrt{8} \) is roughly 2.828.
Applications
- Geometry: The square root of 8 can represent the length of the diagonal of a square with side length 2.
- Physics: It can be used in calculations involving areas and distances in various scientific contexts.
- Engineering: Understanding and simplifying square roots is crucial in designing and analyzing systems and structures.

Conclusion
In conclusion, the square root of 8, expressed in its simplest radical form as \( 2\sqrt{2} \), is an important concept in mathematics. This value is derived through methods like prime factorization and long division, highlighting the underlying structure of numbers. Simplifying square roots, such as that of 8, not only aids in mathematical computations but also enhances our understanding of number properties and relationships.
The approximation of the square root of 8 to three decimal places is 2.828, which is valuable in practical applications where exact precision is not necessary. Recognizing that the square root of 8 is an irrational number, with its non-repeating, non-terminating decimal expansion, enriches our comprehension of different types of numbers in mathematics.
Overall, the ability to simplify and calculate square roots is a fundamental skill that has applications in various fields, including engineering, physics, and computer science. By mastering these techniques, one can approach complex problems with greater confidence and precision.
Hướng dẫn cách đơn giản hóa căn bậc hai của số 8 (sqrt(8)) một cách dễ hiểu và chi tiết. Thích hợp cho người mới học toán.
Cách Đơn Giản Hóa Căn Bậc Hai của 8: sqrt(8)
READ MORE:
Tìm hiểu cách viết căn bậc hai của số 8 ở dạng đơn giản nhất (radical form). Hướng dẫn chi tiết và dễ hiểu.
Căn Bậc Hai của 8 ở Dạng Đơn Giản Nhất