Topic 8 square root simplified: Discover how to simplify the square root of 8 effortlessly using various methods and practical examples. Master the prime factorization and radical form techniques to simplify square roots efficiently. Learn how to convert the square root of 8 into decimal form and explore different approaches to finding square roots. Dive into example problems and FAQs to solidify your understanding.
Table of Content
- Simplifying the Square Root of 8
- Introduction to Square Roots
- Definition and Properties of Square Roots
- Simplifying the Square Root of 8
- Using the Radical Form
- Square Root of 8 in Decimal Form
- Methods to Find the Square Root
- Example Problems
- Common Questions and Answers
- Additional Practice Problems
- Related Topics
- YOUTUBE: Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 8. Video này giúp bạn hiểu rõ hơn về quá trình tính toán và ứng dụng của căn bậc hai.
Simplifying the Square Root of 8
The square root of 8 can be simplified using various methods. Below, we'll explore these methods in detail, including the exact form, decimal approximation, and prime factorization approach.
Exact Form
The exact form of the square root of 8 is:
This can be further explained as:
- Rewrite 8 as 4 × 2.
- Apply the square root to both factors: √8 = √(4 × 2).
- Simplify using the rule √(a × b) = √a × √b: √8 = √4 × √2.
- Since √4 = 2, we get √8 = 2√2.
Decimal Approximation
The square root of 8 can also be represented as a decimal:
√8 ≈ 2.828
This approximation is useful in practical scenarios where an exact form is not necessary.
Prime Factorization Method
To find the square root of 8 using prime factorization:
- Factorize 8 into its prime factors: 8 = 2 × 2 × 2.
- Apply the square root to the product of these factors: √8 = √(2 × 2 × 2).
- Group the pairs of prime factors: √(2 × 2) × √2 = 2√2.
Thus, using the prime factorization method, we again find that √8 = 2√2.
Examples
Let's consider a practical example:
| Example: | Mr. Smith wants to fence his square garden with an area of 8 square feet. The side length of the garden can be found by taking the square root of 8. |
| Solution: | The side length of the garden is √8 = 2√2 feet. |
Conclusion
In summary, the square root of 8 simplifies to 2√2 in its exact form. The decimal approximation is approximately 2.828. Using the prime factorization method also confirms that the simplest radical form is 2√2.
READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics and is widely used in various fields, including algebra, geometry, and calculus. Understanding square roots is essential for solving quadratic equations, working with exponents, and simplifying expressions.
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\). This relationship can be expressed mathematically as:
\[\sqrt{9} = 3\]
Square roots have several important properties:
- Every positive real number has two square roots: one positive and one negative. For instance, the square roots of 25 are 5 and -5, since \(5 \times 5 = 25\) and \(-5 \times -5 = 25\).
- The square root of zero is zero: \(\sqrt{0} = 0\).
- There are no real square roots for negative numbers. However, in the context of complex numbers, the square root of a negative number can be expressed using imaginary units. For example, \(\sqrt{-1} = i\), where \(i\) is the imaginary unit.
Square roots can be represented in different forms:
- Radical Form: The most common way to denote a square root is using the radical symbol \(\sqrt{}\). For example, the square root of 16 is written as \(\sqrt{16}\).
- Exponential Form: Square roots can also be expressed as an exponent of \(\frac{1}{2}\). For example, \(\sqrt{16}\) can be written as \(16^{\frac{1}{2}}\).
In the next sections, we will explore the methods to simplify square roots, starting with the square root of 8. We will use the prime factorization method and the radical form to achieve the simplest form.
Definition and Properties of Square Roots
Square roots are a crucial concept in mathematics, representing a number that, when multiplied by itself, yields the original number. The square root of a number \(x\) is denoted as \(\sqrt{x}\) or \(x^{\frac{1}{2}}\).
The principal (or positive) square root is the non-negative value of \(\sqrt{x}\). Here are some key properties and definitions:
- Existence: Every non-negative number has a non-negative square root. For example, \(\sqrt{4} = 2\) and \(\sqrt{9} = 3\).
- Uniqueness: The principal square root is unique. Although \(\sqrt{x}\) may refer to both positive and negative roots, by convention, \(\sqrt{x}\) typically denotes the positive root.
- Zero Property: The square root of zero is zero: \(\sqrt{0} = 0\).
- Product Property: The square root of a product is the product of the square roots: \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\). For example, \(\sqrt{36} = \sqrt{4 \times 9} = \sqrt{4} \cdot \sqrt{9} = 2 \cdot 3 = 6\).
- Quotient Property: The square root of a quotient is the quotient of the square roots: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\). For instance, \(\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2}\).
- Non-negativity: For any non-negative number \(x\), \(\sqrt{x} \geq 0\).
Additionally, square roots can be simplified using the following steps:
- Identify the prime factors of the number.
- Pair the prime factors.
- Move one factor from each pair outside the square root.
- Multiply the numbers outside the square root to obtain the simplified form.
For example, let's simplify \(\sqrt{8}\):
First, perform the prime factorization of 8:
- 8 = 2 × 2 × 2
Group the prime factors into pairs:
- (2 × 2) × 2 = 4 × 2
Simplify the square root:
\(\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2}\)
Hence, the simplified form of \(\sqrt{8}\) is \(2\sqrt{2}\).
Understanding these properties and methods is fundamental for simplifying square roots and solving more complex mathematical problems.
Simplifying the Square Root of 8
Simplifying the square root of 8 involves breaking down the number into its prime factors and then simplifying the expression by using the properties of square roots. Here is a step-by-step guide to simplify \(\sqrt{8}\):
- Find the Prime Factorization:
Begin by finding the prime factors of 8. The prime factorization of 8 is:
- 8 = 2 × 2 × 2
- Group the Prime Factors:
Next, group the prime factors into pairs. For the number 8, we have:
- (2 × 2) × 2 = 4 × 2
- Apply the Product Property of Square Roots:
Use the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) to split the square root of the product:
\(\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2}\)
- Simplify the Square Roots:
Now, simplify the square roots of the individual factors:
\(\sqrt{4} = 2\)
So, the expression becomes:
\(\sqrt{4} \times \sqrt{2} = 2 \times \sqrt{2}\)
- Combine the Results:
Finally, combine the results to get the simplified form:
\(\sqrt{8} = 2\sqrt{2}\)
Therefore, the simplified form of the square root of 8 is \(2\sqrt{2}\). This process of simplifying square roots by factoring and using properties of radicals can be applied to other numbers as well.
Using the Radical Form
The radical form is a way of representing square roots using the radical symbol \(\sqrt{}\). Simplifying square roots in radical form involves expressing the number under the radical in its simplest terms. Let's go through the steps to simplify the square root of 8 using the radical form.
- Express the Number Under the Radical:
Begin by writing the number under the square root sign:
\(\sqrt{8}\)
- Find the Prime Factorization:
Determine the prime factors of the number 8. The prime factorization of 8 is:
- 8 = 2 × 2 × 2
- Rewrite Using Prime Factors:
Express the square root of 8 in terms of its prime factors:
\(\sqrt{8} = \sqrt{2 \times 2 \times 2}\)
- Group the Prime Factors:
Group the prime factors in pairs, as pairs of identical factors can be taken out of the radical:
- (2 × 2) × 2 = 4 × 2
- Separate and Simplify:
Apply the property of square roots that allows us to separate the factors:
\(\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2}\)
Since \(\sqrt{4} = 2\), we can simplify further:
\(\sqrt{4} \times \sqrt{2} = 2 \sqrt{2}\)
- Write the Final Simplified Form:
The simplified form of \(\sqrt{8}\) is:
\(2\sqrt{2}\)
Using the radical form, we have simplified the square root of 8 to \(2\sqrt{2}\). This method can be used for simplifying other square roots by expressing them in terms of their prime factors and grouping appropriately.

Square Root of 8 in Decimal Form
The square root of 8 can also be represented in decimal form, which is a non-exact, approximate value. To find the decimal form, you can use a calculator or perform a numerical approximation method. Here is a step-by-step explanation of how to determine the square root of 8 in decimal form:
- Using a Calculator:
Most calculators have a square root function. Simply enter the number 8 and press the square root button (\(\sqrt{}\)). The calculator will display the approximate decimal value of the square root of 8.
- Manual Approximation Method:
To manually approximate the square root of 8, you can use the method of averaging. This involves making an initial guess and then improving the guess iteratively. Here are the steps:
- Start with an initial guess. For example, let’s use 2.8.
- Divide the number 8 by the guess. \( \frac{8}{2.8} \approx 2.857 \)
- Take the average of the guess and the result from the previous step: \( \frac{2.8 + 2.857}{2} \approx 2.8285 \)
- Repeat the process with the new guess until the desired accuracy is achieved. For practical purposes, after a few iterations, you will get a sufficiently accurate value.
- Approximate Value:
The square root of 8 in decimal form is approximately:
\(\sqrt{8} \approx 2.828\)
Thus, when expressed in decimal form, the square root of 8 is approximately 2.828. This value can be useful in various practical applications where a numerical approximation is more convenient than the exact radical form.
Methods to Find the Square Root
There are several methods to find the square root of a number, such as 8. Here, we will explore three common methods: the Prime Factorization Method, the Long Division Method, and using a Calculator. Each method provides a step-by-step approach to simplify or find the square root.
Prime Factorization Method
The prime factorization method involves breaking down the number into its prime factors. Let's find the square root of 8 using this method:
- Find the prime factors of 8:
- 8 can be factored into 2 × 4.
- 4 can be further factored into 2 × 2.
- So, the prime factorization of 8 is 2 × 2 × 2 or \(2^3\).
- Group the prime factors into pairs:
- Since we have \(2^3\), we can group it as (2 × 2) × 2.
- Take one factor from each pair outside the square root:
- \(\sqrt{8} = \sqrt{(2 \times 2) \times 2} = 2\sqrt{2}\).
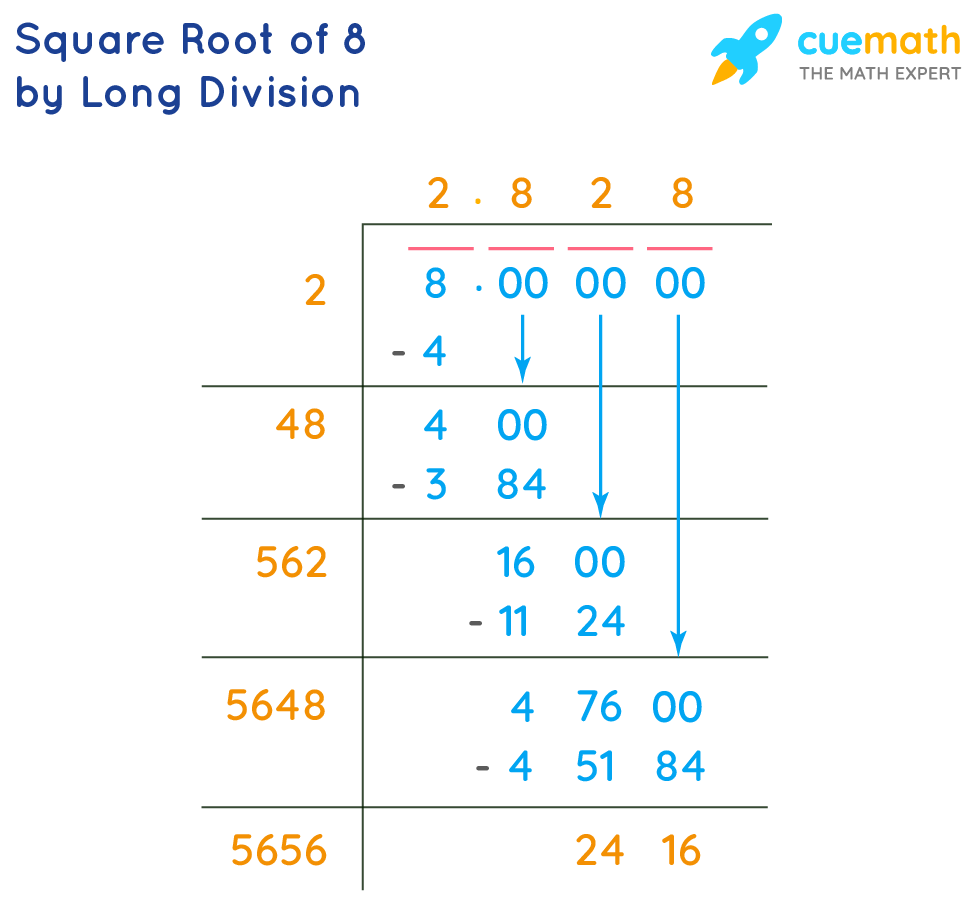
Long Division Method
The long division method is a manual technique to find the square root of a number, which is especially useful when dealing with non-perfect squares:
- Write the number (8) under the square root symbol. Pair the digits starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair (8). In this case, it is 2 (since \(2^2 = 4\)).
- Subtract the square of this number (4) from the first pair (8), and bring down the next pair of zeros (00) to get 400.
- Double the number (2) and write it as the new divisor's first digit (4_). Determine the largest digit (x) such that \(4x \times x\) is less than or equal to 400. The digit is 1 (since \(41 \times 1 = 41\)).
- Subtract and bring down the next pair of zeros. Repeat the process until the desired decimal places are achieved.
- \(\sqrt{8} \approx 2.828\) after performing the long division method up to three decimal places.
Using a Calculator
The simplest way to find the square root of 8 is by using a calculator:
- Turn on the calculator and enter the number 8.
- Press the square root (√) button.
- The calculator will display the result, which is approximately 2.828427124.
Using these methods, you can find the square root of 8 either in its simplified radical form \(2\sqrt{2}\), through long division as approximately 2.828, or directly using a calculator.
Example Problems
Below are several example problems involving the square root of 8. These problems will help you understand how to simplify and use square roots in various contexts.
Example 1: Simplifying the Square Root of 8
Problem: Simplify the square root of 8.
Solution:
- Rewrite 8 as a product of its prime factors: \(8 = 4 \times 2\).
- Take the square root of each factor: \(\sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2}\).
- Simplify: \(\sqrt{4} = 2\), so \(\sqrt{8} = 2\sqrt{2}\).
Therefore, the simplest radical form of \(\sqrt{8}\) is \(2\sqrt{2}\).
Example 2: Finding the Side Length of a Square Garden
Problem: Mr. Smith wants to fence his square garden which has an area of 8 square feet. How long is each side of the garden?
Solution:
- To find the side length of the square garden, we need to find the square root of the area.
- The square root of 8 is \(2\sqrt{2}\).
Therefore, each side of the garden is \(2\sqrt{2}\) feet long.
Example 3: Height of a Gate
Problem: Lucy's gate has an area of 12 square feet. What is the height of the gate if it is square-shaped?
Solution:
- Find the square root of the area: \(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\).
Hence, the height of the gate is \(2\sqrt{3}\) feet.
Example 4: Decimal Form of Square Root of 8
Problem: What is the square root of 8 in decimal form?
Solution:
- We know that \(\sqrt{8} = 2\sqrt{2}\).
- Given \(\sqrt{2} \approx 1.414\), calculate \(2 \times 1.414 \approx 2.828\).
Therefore, the decimal form of \(\sqrt{8}\) is approximately 2.828.
Example 5: Using the Prime Factorization Method
Problem: Simplify the square root of 8 using prime factorization.
Solution:
- Prime factorize 8: \(8 = 2 \times 2 \times 2\).
- Pair the prime factors: \(\sqrt{8} = \sqrt{2 \times 2 \times 2} = \sqrt{(2 \times 2) \times 2} = 2\sqrt{2}\).
Thus, the simplified form is \(2\sqrt{2}\).
Common Questions and Answers
Here are some common questions and answers regarding the square root of 8:
-
Is 8 a perfect square?
No, 8 is not a perfect square. A perfect square is an integer that is the square of another integer. Since there is no integer that when squared gives 8, it is not a perfect square.
-
What is the simplified form of the square root of 8?
The square root of 8 can be simplified by breaking it down into its prime factors. The prime factorization of 8 is \(2 \times 2 \times 2\). We can group the factors in pairs:
\[\sqrt{8} = \sqrt{2 \times 2 \times 2} = \sqrt{4 \times 2} = 2\sqrt{2}\]
-
Is the square root of 8 a rational or irrational number?
The square root of 8 is an irrational number. This is because it cannot be expressed as a fraction of two integers. Its decimal form is non-repeating and non-terminating.
-
What is the decimal form of the square root of 8?
The decimal form of the square root of 8 is approximately 2.82842712474619.
-
How can you calculate the square root of 8 without a calculator?
To calculate the square root of 8 manually, you can use the long division method:
- Set up 8 in pairs of two digits from right to left.
- Find the largest number whose square is less than or equal to 8, which is 2 (since \(2^2 = 4\)).
- Subtract 4 from 8, giving you 4. Bring down a pair of zeros, making it 400.
- Double the number 2 (giving you 4), and determine how many times 4 goes into 400 (ignore the decimal point for now), which is 5. So, the next digit is 5, and you get 25. The process continues.
-
Can the square root of 8 be expressed as a fraction?
No, the square root of 8 cannot be expressed exactly as a fraction since it is an irrational number. However, it can be approximated as a fraction, such as \(\frac{283}{100}\) or \(2\frac{83}{100}\).
-
What is the square root of 8 written with an exponent?
The square root of 8 can be written with an exponent as \(8^{\frac{1}{2}}\).
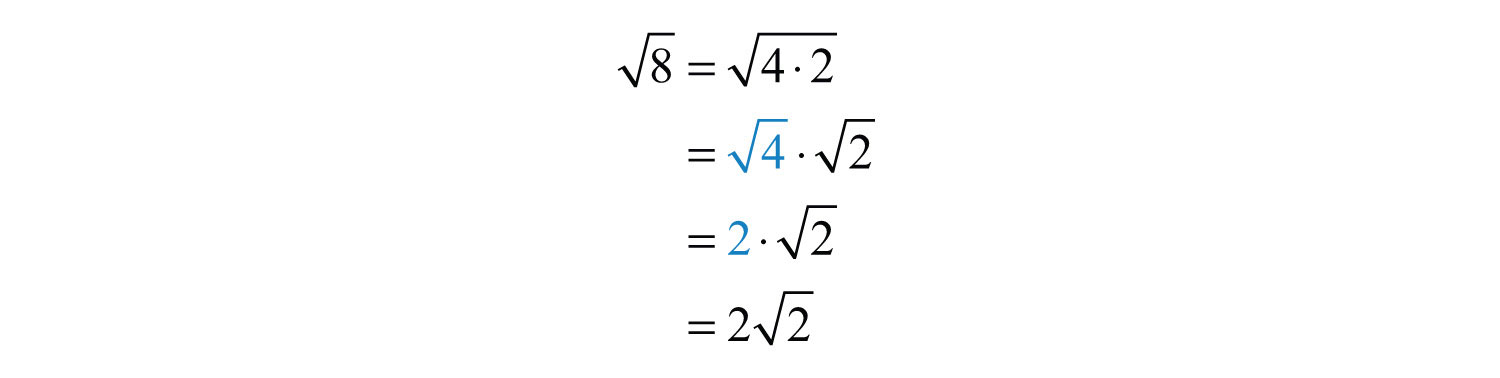
Additional Practice Problems
Below are some additional practice problems to help you master the process of simplifying square roots. Each problem involves simplifying the square root of a given number. Use the steps of prime factorization or the radical form to simplify these square roots.
- Simplify \( \sqrt{18} \)
- Find the prime factorization of 18: \( 18 = 2 \times 3^2 \)
- Group the prime factors into pairs: \( \sqrt{18} = \sqrt{2 \times 3^2} \)
- Extract the square root of the pairs: \( \sqrt{18} = 3 \sqrt{2} \)
- Simplify \( \sqrt{50} \)
- Find the prime factorization of 50: \( 50 = 2 \times 5^2 \)
- Group the prime factors into pairs: \( \sqrt{50} = \sqrt{2 \times 5^2} \)
- Extract the square root of the pairs: \( \sqrt{50} = 5 \sqrt{2} \)
- Simplify \( \sqrt{72} \)
- Find the prime factorization of 72: \( 72 = 2^3 \times 3^2 \)
- Group the prime factors into pairs: \( \sqrt{72} = \sqrt{2^2 \times 2 \times 3^2} \)
- Extract the square root of the pairs: \( \sqrt{72} = 6 \sqrt{2} \)
- Simplify \( \sqrt{98} \)
- Find the prime factorization of 98: \( 98 = 2 \times 7^2 \)
- Group the prime factors into pairs: \( \sqrt{98} = \sqrt{2 \times 7^2} \)
- Extract the square root of the pairs: \( \sqrt{98} = 7 \sqrt{2} \)
Steps:
Steps:
Steps:
Steps:
Use these problems to practice your skills and build confidence in simplifying square roots. Remember to look for pairs of prime factors that can be taken out of the radical.
Challenging Problems
- Simplify \( \sqrt{200} \)
- Find the prime factorization of 200: \( 200 = 2^3 \times 5^2 \)
- Group the prime factors into pairs: \( \sqrt{200} = \sqrt{2^2 \times 2 \times 5^2} \)
- Extract the square root of the pairs: \( \sqrt{200} = 10 \sqrt{2} \)
- Simplify \( \sqrt{288} \)
- Find the prime factorization of 288: \( 288 = 2^5 \times 3^2 \)
- Group the prime factors into pairs: \( \sqrt{288} = \sqrt{2^4 \times 2 \times 3^2} \)
- Extract the square root of the pairs: \( \sqrt{288} = 12 \sqrt{2} \)
Steps:
Steps:
These challenging problems will help you apply the concepts to larger numbers and reinforce your understanding of simplifying square roots.
Related Topics
-
Square Roots of Other Numbers:
-
Methods of Simplifying Square Roots:
-
Properties of Square Roots:
- Square roots of non-perfect squares are irrational numbers.
- Square root is the inverse operation of squaring a number.
- Methods to approximate square roots of non-perfect squares.
-
Applications of Square Roots:
- Using square roots to solve quadratic equations.
- Applying square roots in geometry, such as finding the side length of squares given the area.
- Understanding the use of square roots in physics for calculating distances and areas.
-
Historical Context and Development:
- Historical methods of finding square roots.
- Evolution of numerical methods for square roots.
- Notable mathematicians who contributed to the development of square root calculations.
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của 8. Video này giúp bạn hiểu rõ hơn về quá trình tính toán và ứng dụng của căn bậc hai.
Làm Thế Nào Để Đơn Giản Hóa Căn Bậc Hai Của 8: sqrt(8)
READ MORE:
Khám phá cách viết căn bậc hai của 8 ở dạng đơn giản nhất. Video này sẽ hướng dẫn bạn cách tính toán và hiểu rõ hơn về căn bậc hai của 8.
Căn Bậc Hai Của 8 Ở Dạng Đơn Giản Nhất