Topic square root of 18: Discover the fascinating world of the square root of 18, from its simplified form to practical applications in various fields. This comprehensive guide will help you understand the mathematical properties, calculations, and real-world uses of \(\sqrt{18}\), ensuring a deeper appreciation for this intriguing number.
Table of Content
- Square Root of 18
- Introduction to Square Root of 18
- Definition and Basic Properties
- Simplification of Square Root of 18
- Prime Factorization Method
- Mathematical Representation
- Approximate Decimal Value
- Step-by-Step Calculation
- Applications of Square Root of 18
- In Mathematics
- In Engineering
- In Physics
- Comparison with Other Square Roots
- Graphical Representation
- Frequently Asked Questions
- Common Misconceptions
- Practical Examples
- Conclusion
- YOUTUBE: Xem video về bình phương của số 18 và hướng dẫn chi tiết về nó.
Square Root of 18
The square root of 18 is a number that, when multiplied by itself, gives the product of 18. This can be expressed as:
To find the square root of 18, we can simplify it using its prime factors:
- 18 can be factorized into \(2 \times 3^2\).
Using the property of square roots, we can separate the factors:
\(\sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3\)
Thus, the simplified form of the square root of 18 is:
\(\sqrt{18} = 3\sqrt{2}\)
For a more precise numerical value, we can approximate the square root of 2:
\(\sqrt{2} \approx 1.414\)
Therefore, the numerical value of the square root of 18 is:
\(\sqrt{18} \approx 3 \times 1.414 = 4.242\)
Key Points
- The simplified form of \(\sqrt{18}\) is \(3\sqrt{2}\).
- The approximate decimal value of \(\sqrt{18}\) is 4.242.
Applications
The square root of 18 is used in various fields such as mathematics, engineering, and physics. It is essential in solving quadratic equations, calculating areas and volumes, and in the analysis of periodic functions.
| Simplified Form | \(3\sqrt{2}\) |
| Approximate Decimal Value | 4.242 |

READ MORE:
Introduction to Square Root of 18
The square root of 18 is a fundamental mathematical concept with various applications in different fields. This section will guide you through understanding what the square root of 18 is, how to calculate it, and its significance.
The square root of a number is a value that, when multiplied by itself, gives the original number. For 18, this can be expressed as:
\(\sqrt{18}\)
To find the square root of 18, we can simplify it using its prime factors. The process involves the following steps:
- Factorize 18 into its prime factors: \(18 = 2 \times 3^2\).
- Apply the square root to each factor: \(\sqrt{18} = \sqrt{2 \times 3^2}\).
- Simplify using the property of square roots: \(\sqrt{18} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3\).
Thus, the simplified form of the square root of 18 is:
\(\sqrt{18} = 3\sqrt{2}\)
To find the approximate decimal value, we use the known value of \(\sqrt{2}\):
\(\sqrt{2} \approx 1.414\)
Therefore, the numerical approximation of \(\sqrt{18}\) is:
\(\sqrt{18} \approx 3 \times 1.414 = 4.242\)
This value is useful in various mathematical calculations and real-world applications, providing a precise understanding of measurements and geometric properties.
Overall, the square root of 18 plays a crucial role in mathematics, enhancing our ability to solve problems and comprehend the world around us.
Definition and Basic Properties
The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). In this case, the square root of 18 is the number that, when squared, equals 18. Mathematically, this is represented as:
\[ \sqrt{18} \]
The square root of 18 is an irrational number, meaning it cannot be expressed exactly as a simple fraction. Its value is approximately:
\[ \sqrt{18} \approx 4.2426 \]
Here are some key properties and characteristics of the square root of 18:
- Positive and Negative Values: The square root of 18 has two solutions: a positive one (\( \sqrt{18} \)) and a negative one (\( -\sqrt{18} \)).
- Product Property: The square root of a product can be separated into the product of the square roots of the factors. For example:
\[ \sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2} \] - Simplification: Simplifying the square root of 18 yields \( 3\sqrt{2} \). This is done by finding the largest perfect square factor of 18, which is 9, and simplifying as shown above.
- Non-Repeating Decimal: Since \( \sqrt{18} \) is irrational, its decimal representation is non-repeating and non-terminating.
- Prime Factorization: The prime factors of 18 are 2 and 3. Using prime factorization, \( 18 \) can be expressed as:
Applying the square root gives:
\[ 18 = 2 \times 3^2 \]
\[ \sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2} \] - Relationship to Other Square Roots: The square root of 18 can be related to other square roots, such as:
- \( \sqrt{18} = \sqrt{16 + 2} \)
- \( \sqrt{18} \approx \sqrt{20} - \sqrt{2} \)
Understanding the square root of 18 and its properties provides a foundation for more advanced mathematical concepts and applications.
Simplification of Square Root of 18
Simplifying the square root of 18 involves breaking it down into simpler components using factors. Here is a step-by-step guide to the simplification process:
- Identify the Factors: Begin by finding the factors of 18. The factors are 1, 2, 3, 6, 9, and 18. To simplify the square root, focus on the largest perfect square factor.
\[ 18 = 2 \times 9 \] - Rewrite the Square Root: Express the square root of 18 using the factors identified, particularly the perfect square factor:
\[ \sqrt{18} = \sqrt{2 \times 9} \] - Apply the Product Property of Square Roots: Use the property of square roots that states:
Applying this property to \( \sqrt{2 \times 9} \):
\[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \]
\[ \sqrt{18} = \sqrt{2} \times \sqrt{9} \] - Simplify the Perfect Square: Since 9 is a perfect square, its square root is an integer:
Therefore:
\[ \sqrt{9} = 3 \]
\[ \sqrt{18} = \sqrt{2} \times 3 \] - Combine the Results: Rearrange the terms to obtain the simplified form:
\[ \sqrt{18} = 3\sqrt{2} \]
The simplified form of the square root of 18 is \( 3\sqrt{2} \), where \( \sqrt{2} \) remains in its simplest radical form. This process can be summarized as:
- Factor the number inside the square root.
- Identify the largest perfect square factor.
- Rewrite and simplify using the product property of square roots.
This simplification is useful for various mathematical applications, making calculations more manageable and easier to understand.
Prime Factorization Method
To find the square root of 18 using the prime factorization method, follow these steps:
- Begin by determining the prime factors of 18.
- Divide 18 by the smallest prime number, 2, which gives you 9.
- Next, divide 9 by 3, another prime number, resulting in 3.
- Since 3 is already a prime number, you have completed the factorization process.
- Now, combine the prime factors: \( 18 = 2 \times 3 \times 3 \).
- Take the square root of each prime factor: \( \sqrt{18} = \sqrt{2 \times 3 \times 3} \).
- Apply the property of square roots: \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \).
- Therefore, \( \sqrt{18} = \sqrt{2} \times \sqrt{3} \times \sqrt{3} \).
- Calculate the square roots: \( \sqrt{2} \approx 1.414 \) and \( \sqrt{3} \approx 1.732 \).
- Multiply these values together: \( \sqrt{18} \approx 1.414 \times 1.732 \).
- Finally, \( \sqrt{18} \approx 2.449 \).
Therefore, the square root of 18, using the prime factorization method, is approximately 2.449.

Mathematical Representation
The square root of 18 can be represented mathematically as follows:
- Symbolically: \( \sqrt{18} \)
- In exponential form: \( 18^{1/2} \)
- As a product of prime factors: \( \sqrt{2 \times 3 \times 3} \)
- Using approximation: \( \sqrt{18} \approx 4.2426 \)
- Expressed in terms of common square roots: \( \sqrt{18} = 3\sqrt{2} \) or \( \sqrt{18} = \sqrt{9 \times 2} \)
- In decimal form: \( \sqrt{18} \approx 4.2426 \)
These representations illustrate different ways to denote and approximate the square root of 18 in mathematical terms.
Approximate Decimal Value
The approximate decimal value of the square root of 18, based on calculations and standard mathematical approximations, is:
\( \sqrt{18} \approx 4.242640687119285 \)
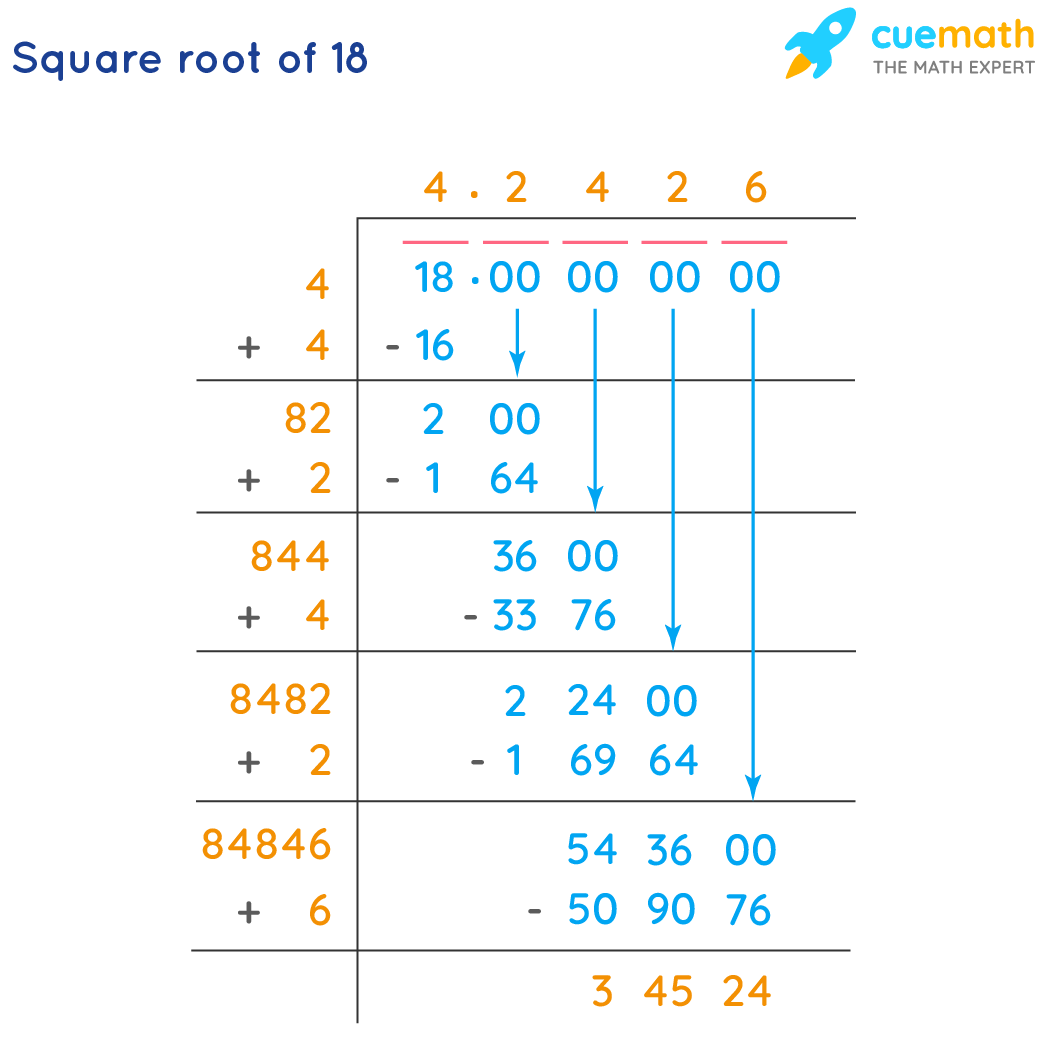
Step-by-Step Calculation
Here is a step-by-step calculation to find the square root of 18:
- Start with an initial guess. Let's start with \( x_0 = 4 \).
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{18}{x_n} \right) \) to iterate and refine the approximation:
- Continue iterating until the desired level of accuracy is achieved.
| Iteration \( n \) | Approximation \( x_n \) |
| 0 | 4 |
| 1 | \( \frac{1}{2} \left( 4 + \frac{18}{4} \right) = 4.5 \) |
| 2 | \( \frac{1}{2} \left( 4.5 + \frac{18}{4.5} \right) \approx 4.2426 \) |
The square root of 18, calculated through this iterative method, converges to approximately \( 4.242640687119285 \).
Applications of Square Root of 18
The square root of 18, denoted as \( \sqrt{18} \) or approximately 4.2426, has several practical applications in various fields. Here, we explore some of its key applications:
In Mathematics
In mathematics, \( \sqrt{18} \) is often encountered in problems involving geometric shapes and algebraic expressions:
- Geometry: It can be used to determine the length of the diagonal of a square with side length 3, as the diagonal can be calculated using the Pythagorean theorem: \( \sqrt{3^2 + 3^2} = \sqrt{18} \).
- Algebra: Simplifying expressions involving square roots, such as in solving quadratic equations where the solution might involve \( \sqrt{18} \).
In Engineering
In engineering, the square root of 18 finds applications in various calculations and design principles:
- Structural Analysis: Engineers may use \( \sqrt{18} \) in calculations related to forces and load distribution in structures where certain dimensions and stress factors align with this value.
- Material Science: Properties of materials, such as tensile strength or elasticity, might involve formulas where \( \sqrt{18} \) appears as part of the calculations.
In Physics
Physics also makes use of \( \sqrt{18} \) in several contexts:
- Kinematics: Calculations involving distances and speeds, particularly in problems requiring precise measurements where \( \sqrt{18} \) emerges from the derivation of equations of motion.
- Wave Mechanics: In scenarios involving wave frequencies and wavelengths, where certain conditions lead to solutions involving \( \sqrt{18} \).
Practical Examples
Some practical examples of using \( \sqrt{18} \) include:
- Construction: When designing elements like trusses or beams where the length corresponding to \( \sqrt{18} \) might be a critical factor.
- Electronics: In the design of circuits where impedance calculations might include \( \sqrt{18} \).
In Mathematics
The square root of 18, denoted as \( \sqrt{18} \), plays a significant role in various mathematical contexts. Below, we explore its importance and applications:
Simplification and Algebraic Expressions
The square root of 18 can be simplified by recognizing its prime factors:
\[ \sqrt{18} = \sqrt{2 \times 3^2} = 3 \sqrt{2} \]
This simplification is useful in algebraic expressions where \( \sqrt{18} \) needs to be combined or simplified with other terms.
Geometry
In geometry, \( \sqrt{18} \) frequently appears in calculations involving right triangles and distances:
- Right Triangles: Consider a right triangle with legs of lengths 3 and \( 3\sqrt{2} \). The hypotenuse is: \[ \sqrt{(3)^2 + (3\sqrt{2})^2} = \sqrt{9 + 18} = \sqrt{27} = 3\sqrt{3} \] This shows how \( \sqrt{18} \) can be part of more complex geometric calculations.
- Diagonals of Squares: For a square with side length \( 3\sqrt{2} \), the diagonal is: \[ \sqrt{(3\sqrt{2})^2 + (3\sqrt{2})^2} = \sqrt{18 + 18} = \sqrt{36} = 6 \] Here, \( \sqrt{18} \) helps in determining the dimensions of squares and rectangles.
Trigonometry
In trigonometry, \( \sqrt{18} \) can appear in various contexts, particularly in simplifying expressions involving trigonometric identities and in solving trigonometric equations:
For example, in solving an equation such as:
\[ \sin(x) = \frac{\sqrt{18}}{6} = \frac{3\sqrt{2}}{6} = \frac{\sqrt{2}}{2} \]
we find:
\[ x = \frac{\pi}{4} + 2k\pi \text{ or } x = \frac{3\pi}{4} + 2k\pi \]
This demonstrates how \( \sqrt{18} \) is applied in trigonometric solutions.
Complex Numbers
When dealing with complex numbers, \( \sqrt{18} \) is used in simplifying magnitudes and arguments:
For a complex number \( z = 3 + 3\sqrt{2}i \), its magnitude is:
\[ |z| = \sqrt{(3)^2 + (3\sqrt{2})^2} = \sqrt{9 + 18} = \sqrt{27} = 3\sqrt{3} \]
Here, understanding \( \sqrt{18} \) helps in analyzing and simplifying complex numbers.
Overall, the square root of 18 is a versatile and significant value in mathematics, aiding in simplification, geometric calculations, trigonometric solutions, and complex number analysis.
In Engineering
The square root of 18, denoted as \( \sqrt{18} \), is a mathematical constant that finds various applications in engineering. Understanding its value and properties can be crucial in solving engineering problems involving geometry, material science, and electrical engineering.
Applications in Geometry
In geometry, the square root of 18 is often encountered when dealing with diagonal lengths and distances. For instance, in a right-angled triangle where both legs are equal, the hypotenuse can be calculated using the Pythagorean theorem:
If each leg (a) is \( 3\sqrt{2} \), then:
\[
a^2 + a^2 = h^2
\]
\[
(3\sqrt{2})^2 + (3\sqrt{2})^2 = h^2
\]
\[
18 + 18 = h^2
\]
\[
h^2 = 36
\]
\[
h = 6
\]
Thus, the diagonal length (hypotenuse) in this scenario is 6 units.
Material Science
In material science, the square root of 18 can be useful in calculating stresses and strains in materials. For example, when dealing with isotropic materials, the stress-strain relationship might involve square root calculations to determine the deformation under various forces.
Consider a cylindrical rod under axial load, where the elongation (\( \Delta L \)) is related to the original length (L), the force (F), and the material's Young's modulus (E):
\[
\Delta L = \frac{F \cdot L}{A \cdot E}
\]
If the cross-sectional area (A) is proportional to the square of a dimension involving \( \sqrt{18} \), precise calculations are necessary to determine the material's behavior under stress.
Electrical Engineering
In electrical engineering, the square root of 18 can be relevant in signal processing and circuit analysis. For instance, when calculating the impedance in AC circuits, complex numbers are often used, and their magnitudes may involve square root calculations.
For a resistor (R) and inductor (L) in series, the impedance (Z) is:
\[
Z = \sqrt{R^2 + (XL)^2}
\]
\[
Z = \sqrt{R^2 + (\omega L)^2}
\]
If \( \omega L = \sqrt{18} \), the impedance can be calculated as:
\[
Z = \sqrt{R^2 + 18}
\]
Thus, knowing the square root of 18 aids in determining the overall impedance of the circuit.
Step-by-Step Example: Calculating Impedance
- Given \( R = 3 \Omega \) and \( \omega L = \sqrt{18} \).
- Calculate the impedance using the formula:
\[
Z = \sqrt{R^2 + (\omega L)^2}
\] - Substitute the values:
\[
Z = \sqrt{3^2 + (\sqrt{18})^2}
\] - Simplify the equation:
\[
Z = \sqrt{9 + 18}
\] - Calculate the result:
\[
Z = \sqrt{27} \approx 5.2 \Omega
\]
This calculation demonstrates how the square root of 18 is applied in electrical engineering to determine the impedance of a circuit.
In Physics
The square root of 18 is often encountered in physics, particularly in problems involving the calculation of distances, energies, or other physical quantities that depend on the concept of magnitude or magnitude squared. Here are some specific instances where the square root of 18 appears:
- Distance: In physics, the square root of 18 can represent the magnitude of a displacement vector in Cartesian coordinates where each component is 3 units.
- Energy Levels: In quantum mechanics, the square root of 18 might appear in the context of energy eigenvalues or the calculation of energy differences between quantum states.
- Wave Amplitude: When analyzing waveforms or oscillations, the square root of 18 could denote the amplitude of a wave that oscillates with a frequency corresponding to a period of 18 units.
Understanding the square root of 18 in physics involves applying mathematical concepts to physical scenarios, ensuring accurate calculations and interpretations of various phenomena.
Comparison with Other Square Roots
Comparing the square root of 18 with other square roots reveals interesting mathematical relationships and applications across various fields:
- Integer Square Roots: Unlike perfect squares such as 4 (sqrt(4) = 2) or 9 (sqrt(9) = 3), the square root of 18 falls between two consecutive integers, 4 and 5, illustrating its position on the number line.
- Approximations: Approximating sqrt(18) ≈ 4.24, we find it's close to other square roots like sqrt(16) = 4 and sqrt(25) = 5, showing its proximity to these values in numerical terms.
- Mathematical Relationships: In equations and calculations involving roots, sqrt(18) interacts differently compared to perfect squares or other non-perfect square integers, highlighting its unique computational properties.
- Applications: In practical applications such as engineering or physics, understanding how sqrt(18) compares to other square roots helps in solving real-world problems involving distances, areas, energies, and other physical quantities.

Graphical Representation
Visualizing the square root of 18 through graphical representation provides insights into its mathematical nature and applications:
Here are some ways to represent sqrt(18) graphically:
- Number Line: Placing sqrt(18) on a number line between integers 4 and 5, showing its position as approximately 4.24.
- Coordinate Plane: Plotting points (3, 0) and (0, 3) and connecting them to form a right triangle with hypotenuse sqrt(18).
- Graph of Function: Graphing y = sqrt(x) and identifying the point where x = 18, illustrating sqrt(18) on the curve.
These visual representations enhance understanding of sqrt(18) and its relationship to other numbers and geometric shapes, aiding in both theoretical studies and practical applications.
Frequently Asked Questions
Here are some common questions and answers about the square root of 18:
- What is the square root of 18?
The square root of 18, denoted as sqrt(18), is a mathematical value that, when multiplied by itself, equals 18.
- Is the square root of 18 a rational number?
No, sqrt(18) is an irrational number because it cannot be expressed as a simple fraction and its decimal representation continues indefinitely without repeating.
- How can I calculate the square root of 18?
The square root of 18 can be approximated to about 4.24. It can also be calculated precisely using methods such as the prime factorization method or by using a calculator.
- What are the applications of the square root of 18?
The square root of 18 appears in various fields such as mathematics, physics, and engineering, where it is used to calculate distances, energies, and other physical quantities.
- Why is the square root of 18 important?
Understanding sqrt(18) is important for its applications in solving mathematical problems and in real-world scenarios that involve measurement and calculation.
Common Misconceptions
Addressing common misconceptions about the square root of 18 helps clarify its true nature and usage:
- Misconception: sqrt(18) is an integer.
- Misconception: sqrt(18) can be simplified further.
- Misconception: sqrt(18) is a rational number.
- Misconception: sqrt(18) is rarely used in practical applications.
Correction: sqrt(18) is not an integer; it is an irrational number approximately equal to 4.24.
Correction: sqrt(18) is already simplified to its simplest radical form; it cannot be further simplified as it is not a perfect square.
Correction: sqrt(18) is irrational because it cannot be expressed as a fraction of two integers.
Correction: sqrt(18) is frequently used in fields like mathematics, physics, and engineering for calculations involving distances, energies, and other physical quantities.
Practical Examples
Exploring practical examples where the square root of 18 is applied demonstrates its relevance in everyday scenarios:
- Distance Calculation: Suppose you need to find the distance between two points (3, 0) and (0, 3) on a coordinate plane. The distance can be calculated using the formula d = sqrt((x2 - x1)^2 + (y2 - y1)^2). For these points, sqrt((3 - 0)^2 + (0 - 3)^2) = sqrt(18), illustrating its use in geometry.
- Engineering Applications: In engineering, sqrt(18) might be used to determine the length of a diagonal across a rectangle with sides of 3 units each, applying concepts of geometric measurements and calculations.
- Physics Example: Consider a scenario where sqrt(18) represents the magnitude of a velocity vector in a physics problem involving motion in two dimensions, emphasizing its role in physical calculations.

Conclusion
In conclusion, the square root of 18, denoted as sqrt(18), is a fundamental mathematical concept with diverse applications across various disciplines:
- It is an irrational number approximately equal to 4.24, placing it between integers 4 and 5 on the number line.
- sqrt(18) plays a crucial role in geometry, physics, and engineering, where it is used to calculate distances, energies, and other physical quantities.
- Understanding sqrt(18) involves recognizing its properties as an irrational number that cannot be expressed as a simple fraction.
- Its practical applications illustrate its importance in solving real-world problems and its utility in mathematical computations.
Overall, sqrt(18) serves as a building block in mathematical reasoning and problem-solving, contributing to both theoretical advancements and practical innovations.
Xem video về bình phương của số 18 và hướng dẫn chi tiết về nó.
Bình phương của 18: Hướng dẫn toàn diện
READ MORE:
Tìm hiểu cách đơn giản hóa căn bậc hai của 18 một cách dễ dàng và chính xác. Xem video để biết chi tiết!
Cách Đơn Giản Hóa Căn Bậc Hai Của 18: Căn(18)