Is the Square Root of 8 a Rational Number? Unveiling the Truth

To determine whether the square root of 8 is a rational number, we need to understand the definition of rational and irrational numbers. A rational number is a number that can be expressed as the quotient or fraction of two integers, where the numerator and denominator are both integers, and the denominator is not zero.

Understanding Rational and Irrational Numbers

• Rational numbers include integers, finite decimals, and repeating decimals.
• Irrational numbers cannot be expressed as a simple fraction. Their decimal representation is non-terminating and non-repeating.

Examples of rational numbers are:

• 5 (which can be written as 5/1)
• 0.75 (which can be written as 3/4)
• 0.333... (which is 1/3)

Examples of irrational numbers are:

• π (Pi)
• e (Euler's Number)

The Square Root of 8

The square root of 8 is expressed as √8 or approximately 2.82842712475. To determine if it is rational, consider the following:

1. The prime factorization of 8 is 2³. For the square root to be rational, all prime factors must be in pairs.
2. Since 2³ is not a perfect square (pairs of primes), √8 cannot be simplified to a fraction of two integers.

Therefore, the square root of 8 is irrational because it cannot be expressed as a fraction of two integers, and its decimal form is non-terminating and non-repeating.

Additional Information

In simplest radical form, the square root of 8 is written as 2√2. This form highlights its irrationality as it still involves an irrational component (√2).

For practical applications, you may use the approximate decimal value (2.828) but remember that this is an approximation, not an exact value.

The square root of 8 is an irrational number. It cannot be expressed as a simple fraction, and its decimal representation continues infinitely without repeating. Understanding the properties of rational and irrational numbers helps in various mathematical contexts and real-life applications.

The square root of 8 is an irrational number. It cannot be expressed as a simple fraction, and its decimal representation continues infinitely without repeating. Understanding the properties of rational and irrational numbers helps in various mathematical contexts and real-life applications.

Understanding the nature of numbers is fundamental in mathematics. Numbers can be broadly categorized into two types: rational and irrational. Let’s explore these categories step by step:

Rational Numbers

• Rational numbers are numbers that can be expressed as the quotient or fraction $\frac{a}{b}$, where a and b are integers and b is not zero.
• Examples include $\frac{1}{2}$, 3 (which can be written as $\frac{3}{1}$), and -4.5 (which can be written as $\frac{-9}{2}$).
• They have a finite or repeating decimal representation.

Irrational Numbers

• Irrational numbers cannot be expressed as a simple fraction; their decimal representation is non-repeating and infinite.
• Examples include $\sqrt{2}$ and π (pi).
• They fill the gaps between rational numbers on the number line, contributing to the continuum of real numbers.

In summary, while rational numbers are those that can be written as fractions, irrational numbers cannot be represented in such a form, offering a unique and fascinating dimension to the field of mathematics.

Rational numbers are a fundamental concept in mathematics, characterized by their ability to be expressed as fractions. Here, we break down the definition and properties of rational numbers step by step:

What is a Rational Number?

• A rational number is any number that can be written as a fraction $\frac{a}{b}$, where a and b are integers and b is not zero.
• This form is also known as a ratio, hence the term "rational" numbers.

Examples of Rational Numbers

• Simple fractions: $\frac{1}{2}$, $\frac{3}{4}$
• Integers: 5 (which can be written as $\frac{5}{1}$), -7 (which can be written as $\frac{-7}{1}$)
• Decimals that terminate or repeat: 0.75 (which can be written as $\frac{3}{4}$), 0.333... (which can be written as $\frac{1}{3}$)

Properties of Rational Numbers

• Closure: Rational numbers are closed under addition, subtraction, multiplication, and division (except by zero).
• Commutativity: The addition and multiplication of rational numbers are commutative, meaning $a+b=b+a$ and $a\times b=b\times a$.
• Associativity: Addition and multiplication are associative, meaning $(a+b)+c=a+(b+c)$ and $(a\times b)\times c=a\times (b\times c)$.

By understanding these properties and examples, we can clearly see how rational numbers form an integral part of our number system, providing a solid foundation for further mathematical concepts.

Irrational numbers are numbers that cannot be expressed as a simple fraction, meaning they cannot be written as the ratio of two integers. In mathematical terms, a number x is considered irrational if it cannot be written in the form a/b, where a and b are integers and b ≠ 0.

The decimal representation of an irrational number is non-terminating and non-repeating. This means that the digits after the decimal point continue indefinitely without forming a repeating pattern.

Some common examples of irrational numbers include:

• π (Pi), the ratio of the circumference of a circle to its diameter.
• e, the base of the natural logarithm.
• √2, the square root of 2, which cannot be simplified to a fraction.

To illustrate why a number is irrational, consider the square root of 2. Suppose √2 is rational, meaning it can be written as a/b in its simplest form where a and b are coprime integers. Then, √2 = a/b implies 2 = a²/b², and hence 2b² = a². This shows that a² is even, so a must also be even. Let a = 2k. Substituting, we get 2b² = (2k)², which simplifies to 2b² = 4k², or b² = 2k². This shows that b² is even, so b must also be even. However, this contradicts our assumption that a and b are coprime. Therefore, √2 must be irrational.

This same type of proof can be used to show that the square root of any non-perfect square is irrational. Therefore, the square root of 8, like the square root of 2, is also irrational because 8 is not a perfect square.

Understanding irrational numbers is crucial in various fields of mathematics and science, as they often appear in natural phenomena and complex calculations. Recognizing their properties helps in developing a deeper comprehension of the mathematical universe.

The square root of 8, denoted as √8, is a number that, when multiplied by itself, gives the product 8. Mathematically, this can be expressed as:

\[ \sqrt{8} = x \quad \text{such that} \quad x^2 = 8 \]

To understand whether √8 is a rational number, we first need to determine if it can be expressed as the ratio of two integers. Let's explore this step by step:

1. Simplifying √8: The number 8 can be factored into its prime components:

   \[ 8 = 2 \times 2 \times 2 = 2^3 \]

   Therefore, √8 can be simplified using the properties of square roots:

   \[ \sqrt{8} = \sqrt{2^3} = \sqrt{2^2 \times 2} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} \]

2. Analyzing 2√2: Now, we need to determine if √2 is a rational number. It is well-known that √2 is an irrational number. Since multiplying a rational number (2) by an irrational number (√2) results in an irrational number, 2√2 is also irrational.

From the above steps, we can conclude that:

\[ \sqrt{8} = 2\sqrt{2} \]

Since √2 is irrational, 2√2 (and hence √8) is also irrational. Therefore, √8 cannot be expressed as a ratio of two integers, confirming that it is indeed an irrational number.

Understanding the properties of the square root of 8 helps us appreciate the broader category of irrational numbers and their significance in mathematical theory and applications.

In mathematics, proving whether a number is rational or irrational is a fundamental exercise. Rational numbers can be expressed as the ratio of two integers, while irrational numbers cannot. Let's explore the mathematical proofs for determining the nature of a number.

Proof that the Square Root of 2 is Irrational

Consider the square root of 2 (√2). We will use a proof by contradiction to show that it is irrational:

1. Assume that √2 is rational. This means it can be written as a fraction a/b, where a and b are coprime integers (having no common factors other than 1).
2. Therefore, √2 = a/b implies that \(2 = a^2 / b^2\).
3. Rewriting gives \(2b^2 = a^2\). This means that a^2 is even (since it is two times some integer), so a must also be even.
4. If a is even, we can write a = 2k for some integer k.
5. Substituting a = 2k into \(2b^2 = a^2\) gives \(2b^2 = (2k)^2\), which simplifies to \(2b^2 = 4k^2\), or \(b^2 = 2k^2\).
6. This shows that b^2 is even, so b must also be even.
7. However, if both a and b are even, they share a common factor of 2, which contradicts the initial assumption that a and b are coprime.
8. Therefore, the assumption that √2 is rational must be false, so √2 is irrational.

Proof that the Square Root of 8 is Irrational

To determine the nature of √8, we first simplify it:

\[ \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} \]

Since we have already established that √2 is irrational, multiplying it by 2 (a rational number) still results in an irrational number. Hence, √8 is also irrational.

General Method to Determine the Rationality of Square Roots

To determine if the square root of a number is rational or irrational, follow these steps:

1. Check if the number is a perfect square. The square root of a perfect square is rational (e.g., √9 = 3).
2. If the number is not a perfect square, its square root is irrational. This can often be shown using a proof by contradiction similar to the one used for √2.

Understanding these proofs helps in distinguishing between rational and irrational numbers and in recognizing the properties that define them.

Determining whether the square root of a number is rational or irrational involves a few key methods and principles. Here, we will explore these methods step by step.

1. Checking for Perfect Squares

A simple method to determine if the square root of a number is rational is to check if the number is a perfect square.

• If a number n can be expressed as k², where k is an integer, then √n is rational.
• Examples include \( \sqrt{4} = 2 \) and \( \sqrt{9} = 3 \), where 4 and 9 are perfect squares.

If the number is not a perfect square, its square root is irrational. For instance, 8 is not a perfect square because there is no integer k such that \( k^2 = 8 \).

2. Prime Factorization Method

Another method involves the prime factorization of the number:

1. Perform prime factorization of the number.
2. Check the exponents of the prime factors in the factorization.
3. If all the prime factors have even exponents, the square root is rational; otherwise, it is irrational.

For example, consider the number 8:

• Prime factorization of 8: \( 8 = 2^3 \).
• Since the exponent of 2 is 3 (an odd number), √8 is irrational.

3. Proof by Contradiction

A rigorous mathematical approach to prove irrationality is proof by contradiction:

1. Assume that √n is rational, meaning it can be expressed as a/b, where a and b are coprime integers.
2. Then \( n = (a/b)^2 \), implying \( n \cdot b^2 = a^2 \).
3. Analyze the resulting equation for contradictions based on the properties of integers.

For example, to prove √8 is irrational:

• Assume √8 is rational: \( \sqrt{8} = a/b \).
• This implies \( 8 = a^2 / b^2 \), or \( 8b^2 = a^2 \).
• Since 8 is \( 2^3 \), substitute and simplify to find that both a and b must be even, which contradicts the assumption that a and b are coprime.

4. Decimal Representation Method

Examining the decimal representation of a square root can also help:

• If the decimal expansion is non-terminating and non-repeating, the number is irrational.

For example, the decimal representation of \( \sqrt{8} \approx 2.82842712474619...\) is non-terminating and non-repeating, confirming its irrationality.

By applying these methods, one can determine the rationality of square roots with confidence and clarity.

The square root of 8 is denoted as \( \sqrt{8} \). Let's explore its calculation and analyze its properties step by step.

Calculation

We can simplify \( \sqrt{8} \) as follows:

1. Prime factorize 8: \( 8 = 2 \times 2 \times 2 \).
2. Express \( \sqrt{8} \) in terms of prime factors: \( \sqrt{8} = \sqrt{2 \times 2 \times 2} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} \).

Therefore, \( \sqrt{8} = 2\sqrt{2} \).

Decimal Representation

The approximate decimal value of \( \sqrt{8} \) is 2.828427125. This value is non-terminating and non-repeating, indicating that \( \sqrt{8} \) is an irrational number.

Analysis

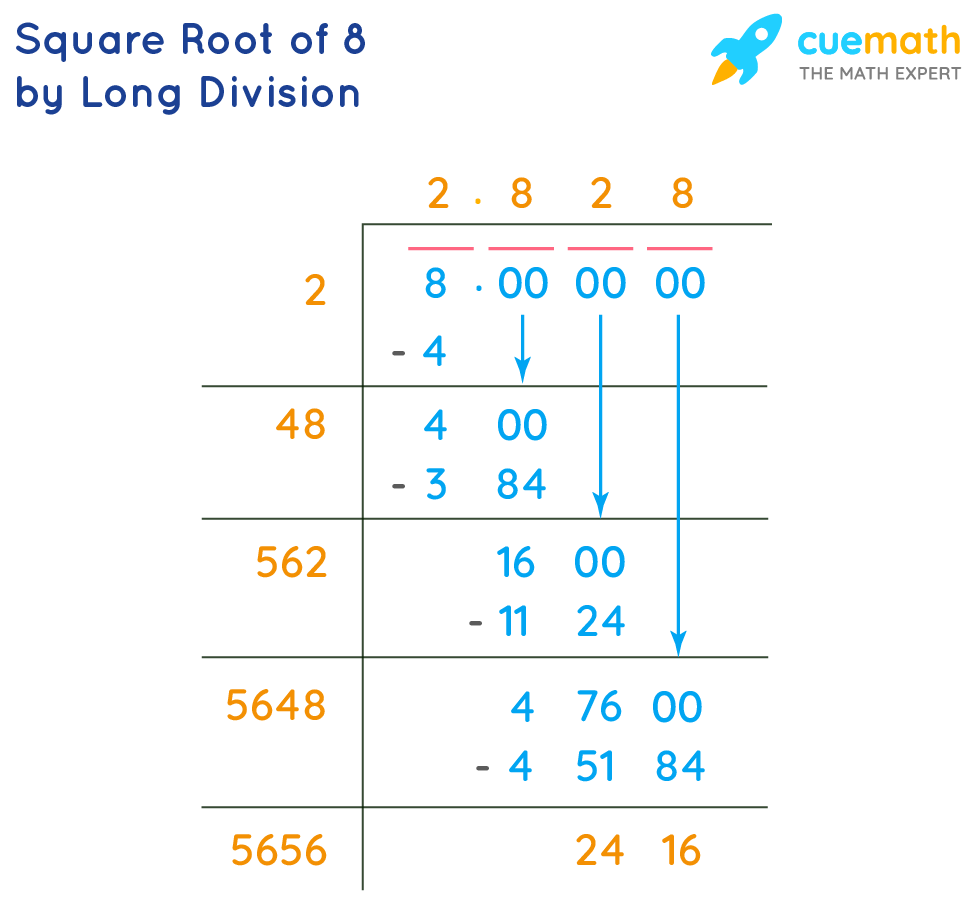
We use the long division method to find the square root of non-perfect squares:

1. Pair the digits starting from the right. For 8, we have one pair.
2. Find a number whose square is less than or equal to 8. This number is 2.
3. Double the divisor (2) and find the next digit to form the new quotient and divisor, repeating the process to achieve the desired precision.

Conclusion

The simplified radical form of \( \sqrt{8} \) is \( 2\sqrt{2} \), and its approximate decimal form is 2.828427125. As it is a non-terminating, non-repeating decimal, \( \sqrt{8} \) is an irrational number.

To understand why the square root of 8 is an irrational number, we must first explore what it means for a number to be rational or irrational.

A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, where p and q are integers and q is not zero. An irrational number, on the other hand, cannot be expressed as a simple fraction; it has a non-repeating, non-terminating decimal expansion.

Now, let's analyze the square root of 8:

• We can simplify the square root of 8 using prime factorization:
  • The prime factorization of 8 is \(8 = 2 \times 2 \times 2\).
  • Therefore, \(\sqrt{8} = \sqrt{2 \times 2 \times 2} = 2\sqrt{2}\).
• Here, \(2\sqrt{2}\) indicates that the square root of 8 is dependent on the square root of 2.
• It is well-known that \(\sqrt{2}\) is an irrational number because it cannot be expressed as a fraction of two integers.
• Since \(\sqrt{2}\) is irrational, \(2\sqrt{2}\) is also irrational, as the product of a rational number (2) and an irrational number (\(\sqrt{2}\)) remains irrational.

Thus, we conclude that the square root of 8 is an irrational number. This is due to the fact that it involves the multiplication of the irrational number \(\sqrt{2}\), which inherently cannot be expressed as a fraction of two integers.

Visualizing the square root of 8 on a number line helps in understanding its position relative to other numbers, especially other irrational numbers. The square root of 8, denoted as \( \sqrt{8} \), is approximately 2.828. This value places it between the integers 2 and 3 on the number line.

To illustrate this, we can follow these steps:

1. Identify Perfect Squares: Note that the perfect square less than 8 is 4 (since \(2^2 = 4\)) and the perfect square greater than 8 is 9 (since \(3^2 = 9\)). This tells us that \( \sqrt{8} \) is between 2 and 3.
2. Approximate Value: The decimal approximation of \( \sqrt{8} \) is 2.828. This means \( \sqrt{8} \) is slightly less than 3 but more than 2.8.
3. Plotting on Number Line: To mark \( \sqrt{8} \) on a number line, locate the points 2 and 3 first. Then, place a mark slightly before 2.83.

We can also use a geometric method to visualize \( \sqrt{8} \). Consider the following steps:

• Construct a Square: Draw a square with an area of 8 square units. Since \( \sqrt{8} \) is the side length of this square, you can visualize this length as the distance on the number line.
• Use a Compass and Ruler: Draw a number line and use a compass set to the length representing \( \sqrt{8} \) to mark its exact position.

By understanding these methods, you can better grasp where \( \sqrt{8} \) fits among other numbers and appreciate its irrational nature. It is not a whole number and cannot be exactly expressed as a simple fraction, making it a fascinating example of an irrational number on the number line.

Irrational numbers, which cannot be expressed as a ratio of two integers, have numerous practical applications in various fields. Here are some examples of how these numbers are used in real life:

• Engineering and Design:

  The number e, also known as Euler's number, is widely used in engineering and design for calculations involving exponential growth and decay, such as in signal processing and designing speedometers.

• Construction:

  The irrational number π (pi) is essential in construction and architecture, especially when dealing with circular structures. It is used to calculate the circumference and area of circles, which is critical for designing anything with circular components.

• Finance:

  In finance, irrational numbers can be used to calculate compound interest. For example, the sum of an infinite geometric series involving an irrational number can be used to determine compound interest rates.

• Nature and Biology:

  Many natural patterns and phenomena can be described using irrational numbers. The golden ratio (φ) appears in various biological structures, such as the spirals of shells and the branching of trees.

• Art and Music:

  The golden ratio is also prevalent in art and music. It is used to achieve aesthetically pleasing proportions in visual art and architecture. In music, irrational numbers can help in tuning systems and the analysis of sound waves.

These examples illustrate that while irrational numbers may seem abstract, they play a crucial role in our everyday lives and the functioning of various complex systems.

Irrational numbers, such as the square root of 8, hold a unique place in mathematics and the real world. These numbers cannot be expressed as a simple fraction of two integers, making them fascinating and complex.

The square root of 8, denoted as \( \sqrt{8} \), is approximately equal to 2.82842712475 and does not terminate or repeat, confirming its irrationality. This characteristic makes irrational numbers an essential part of mathematical concepts and applications.

To fully appreciate the beauty of irrational numbers, consider the following points:

• Uniqueness: Irrational numbers like \( \sqrt{8} \) are unique because their decimal expansion is infinite and non-repeating.
• Mathematical Proof: The irrationality of \( \sqrt{8} \) can be demonstrated through mathematical proofs, emphasizing the logical foundation of mathematics.
• Geometry: Irrational numbers are crucial in geometry, particularly in calculations involving circles, triangles, and other shapes where precise measurements are needed.
• Real-Life Applications: These numbers appear in various real-life contexts, such as engineering, physics, and computer science, where precise calculations are paramount.
• Infinite Possibilities: The non-repeating nature of irrational numbers suggests the idea of infinity, offering a glimpse into the boundless nature of mathematics.

Embracing irrational numbers like \( \sqrt{8} \) allows us to deepen our understanding of mathematics and its applications. These numbers remind us that while some aspects of the world can be measured and predicted, others remain beautifully complex and infinite.

In conclusion, the irrationality of the square root of 8 and other similar numbers enriches our mathematical knowledge and enhances our appreciation for the intricacies of the universe. By studying and understanding these numbers, we embrace the beauty and wonder of mathematics in its purest form.