Topic how to find square root of 8: Discover simple and effective methods to find the square root of 8 with our comprehensive guide. Whether you're a student or just curious, we'll walk you through various techniques, including manual calculations and using a calculator. Master the process with step-by-step instructions and practical tips to enhance your math skills.
Table of Content
- Search Results: How to Find Square Root of 8
- Introduction to Square Roots
- Understanding Square Roots
- Why Find the Square Root of 8?
- Basic Concepts and Definitions
- Manual Methods to Calculate Square Roots
- Long Division Method
- Prime Factorization Method
- Using Approximation Techniques
- Using a Calculator to Find Square Roots
- Step-by-Step Guide to Finding the Square Root of 8
- Step 1: Estimation
- Step 2: Refining the Estimation
- Step 3: Verification of Results
- Common Mistakes to Avoid
- Advanced Methods for Finding Square Roots
- Newton-Raphson Method
- Babylonian Method
- Square Roots in Real Life Applications
- YOUTUBE: Xem video hướng dẫn cách đơn giản hóa căn bậc hai của số 8 (sqrt(8)).
Search Results: How to Find Square Root of 8
When finding the square root of 8, you can use the following methods:
- Using the factorization method:
8 can be expressed as \( 8 = 4 \times 2 \).
Therefore, \( \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} \).
- Approximation method:
Approximately, \( \sqrt{8} \approx 2.828 \).
- Using a calculator:
Modern calculators can directly compute \( \sqrt{8} \), giving you a precise decimal value.
Additional Information:
Understanding square roots involves fundamental concepts in mathematics and is useful in various applications such as geometry, physics, and engineering.
READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics that involve finding a number which, when multiplied by itself, yields the original number. This number is called the square root, denoted by the radical symbol '√'. For instance, the square root of 9 is 3 because 3 multiplied by itself (3 x 3) equals 9.
Most square roots of non-perfect squares are irrational, meaning their decimal form is non-terminating and non-repeating. These values cannot be expressed as simple fractions. The square root of 8, for example, is approximately 2.82842712475. This is an irrational number since it cannot be precisely expressed as a fraction.
Understanding square roots is crucial for various applications in geometry, algebra, and real-world problem-solving. Here's a brief overview of key points about square roots:
- Square Root Symbol: The square root is represented by '√'. The number under this symbol is called the radicand.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are whole numbers (1, 2, 3, 4, and 5 respectively).
- Approximation: For numbers that are not perfect squares, such as 8, the square root is an approximation. For example, √8 ≈ 2.828.
- Calculation Methods: Square roots can be calculated using methods like long division, approximation techniques, and calculators.
To manually find a square root, one effective technique is the method of averaging, also known as Heron's method. This iterative method involves making an initial guess and refining it through a series of averages until the value stabilizes.
Understanding square roots provides a foundation for exploring more complex mathematical concepts and solving practical problems. By mastering the basics of square roots, you can enhance your mathematical skills and apply them in various scenarios.
Understanding Square Roots
Square roots are fundamental mathematical concepts that are essential for understanding various aspects of algebra, geometry, and real-world applications. At its core, the square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 × 3 = 9.
Mathematically, the square root of a number \( x \) is represented as \( \sqrt{x} \). For instance, the square root of 8 is denoted as \( \sqrt{8} \). The square root function is the inverse of squaring a number.
Properties of Square Roots
- Non-Negative Values: The square root of a non-negative number is always non-negative.
- Product Property: The square root of a product is equal to the product of the square roots of the factors: \( \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Examples
Here are a few examples to illustrate how square roots work:
- \( \sqrt{4} = 2 \) because \( 2 \times 2 = 4 \).
- \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
- \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \).
Square Roots of Non-Perfect Squares
When the number is not a perfect square, its square root is an irrational number, which means it cannot be expressed as a simple fraction and its decimal form goes on forever without repeating. For example:
- \( \sqrt{2} \approx 1.414 \)
- \( \sqrt{3} \approx 1.732 \)
- \( \sqrt{8} \approx 2.828 \)
Calculating Square Roots
There are various methods to calculate square roots, including:
- Prime Factorization: Decomposing the number into its prime factors and simplifying.
- Long Division Method: A manual method that is more precise for larger numbers.
- Using a Calculator: The most convenient method for quick results.
Understanding the concept of square roots and the methods to calculate them is crucial for solving more complex mathematical problems and for practical applications in science, engineering, and daily life.
Why Find the Square Root of 8?
Understanding the importance of finding the square root of 8 can be highly beneficial in various mathematical and real-life contexts. Here are some key reasons:
- Mathematical Concepts: The square root of a number is fundamental in mathematics, especially in algebra and geometry. It helps in solving quadratic equations and in understanding the properties of numbers.
- Approximations: Knowing that the square root of 8 is approximately 2.828 helps in making quick and efficient approximations in calculations without the need for a calculator.
- Geometric Applications: In geometry, the square root of 8 can be used to determine the length of the diagonal of a square with sides of length 2√2.
- Real-Life Situations: Understanding how to find the square root of non-perfect squares like 8 can be applied in various fields such as engineering, physics, and finance, where precise measurements and calculations are required.
- Educational Purposes: Learning how to find the square root manually helps in building a strong mathematical foundation and enhances problem-solving skills.
Overall, finding the square root of 8, despite it being an irrational number, demonstrates a crucial aspect of understanding more complex mathematical operations and their applications in the real world.
Basic Concepts and Definitions
Understanding square roots is fundamental in mathematics. A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). In other words, it is a value that, when multiplied by itself, gives the original number. The square root of a number \( x \) is denoted as \( \sqrt{x} \).
Here are some basic concepts and definitions related to square roots:
- Perfect Squares: A number is a perfect square if it can be expressed as the product of an integer with itself. For example, 4, 9, 16 are perfect squares because \( 2^2 = 4 \), \( 3^2 = 9 \), and \( 4^2 = 16 \).
- Non-Perfect Squares: Numbers that are not perfect squares do not have an integer as their square root. For example, 2, 3, 5, 8 are non-perfect squares.
- Irrational Numbers: The square roots of non-perfect squares are irrational numbers. These numbers cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions. For example, \( \sqrt{2} \approx 1.414 \), \( \sqrt{3} \approx 1.732 \), and \( \sqrt{8} \approx 2.828 \).
- Radical Sign: The symbol \( \sqrt{} \) is called the radical sign, and the number under the radical sign is called the radicand. For example, in \( \sqrt{8} \), 8 is the radicand.
- Principal Square Root: The principal square root is the non-negative square root of a number. For any positive number \( x \), \( \sqrt{x} \) represents the principal square root.
Square roots are important in various mathematical contexts such as solving quadratic equations, calculating areas, and in various fields like physics, engineering, and computer science. Understanding how to find and approximate square roots is essential for higher-level math and practical applications.

Manual Methods to Calculate Square Roots
There are several manual methods to calculate square roots, and they are particularly useful for understanding the fundamental concepts behind square roots. Here, we will explore two popular manual methods: the Long Division Method and the Approximation Method.
Long Division Method
The Long Division Method is a systematic way to find the square root of a number, and it involves the following steps:
- Pairing the Digits: Start by pairing the digits of the number from right to left. For instance, to find the square root of 8, consider it as 8.00 (adding decimal pairs as needed).
- Find the Largest Integer: Find the largest integer whose square is less than or equal to the first pair. For 8, this is 2 because \(2^2 = 4\) and \(3^2 = 9\).
- Subtract and Bring Down: Subtract the square of the integer from the first pair, and bring down the next pair of digits. For 8, subtract 4 from 8 to get 4, and bring down 00 to make it 400.
- Double the Quotient: Double the quotient obtained so far (which is 2 in this case) to get 4, and place it as the new divisor with a blank on its right.
- Find the Next Digit: Find a digit to fill in the blank such that when the new divisor is multiplied by this digit, the product is less than or equal to the current number. For 400, the digit is 5 because \(45 \times 5 = 225\) (which is less than 400).
- Repeat: Repeat the process to get more decimal places as needed. Continue bringing down pairs of zeros and finding digits to fill in the quotient until the desired accuracy is achieved.
Example of Long Division Method for √8
| Step | Calculation |
| 1 | Pair the digits: 8.00 → 8|00 |
| 2 | Largest integer: 2 (because \(2^2 = 4\)) |
| 3 | Subtract and bring down: 8 - 4 = 4, bring down 00 to make it 400 |
| 4 | Double quotient: 2 → 4 |
| 5 | Next digit: 5 (because \(45 \times 5 = 225\)) |
| 6 | New remainder: 400 - 225 = 175, bring down 00 to make it 17500 |
Approximation Method
The Approximation Method is a simpler, iterative method to approximate the square root of a number. Here are the steps:
- Initial Guess: Make an initial guess. For √8, start with 2.
- Improve the Guess: Use the formula \( \text{New guess} = \frac{1}{2} \left(\text{Old guess} + \frac{8}{\text{Old guess}}\right) \). For the first iteration, this gives \( \frac{1}{2} \left(2 + \frac{8}{2}\right) = 3 \).
- Repeat: Repeat the process to improve the accuracy. After a few iterations, the guess converges to the actual square root. For instance, the second iteration gives \( \frac{1}{2} \left(3 + \frac{8}{3}\right) \approx 2.8333 \).
Example of Approximation Method for √8
| Iteration | Calculation |
| 1 | Initial guess: 2 |
| 2 | First iteration: \( \frac{1}{2} \left(2 + \frac{8}{2}\right) = 3 \) |
| 3 | Second iteration: \( \frac{1}{2} \left(3 + \frac{8}{3}\right) \approx 2.8333 \) |
| 4 | Third iteration: \( \frac{1}{2} \left(2.8333 + \frac{8}{2.8333}\right) \approx 2.8284 \) |
Using these manual methods helps in understanding the underlying principles of square roots and improves numerical skills.
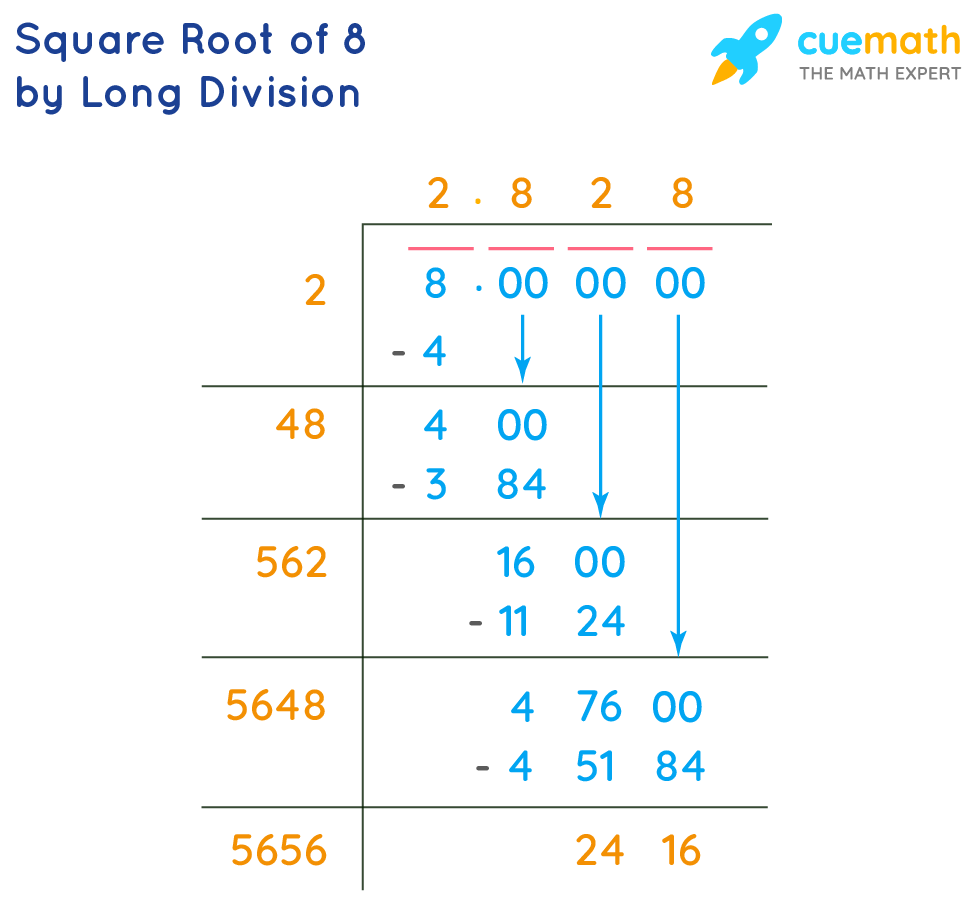
Long Division Method
The long division method is a systematic way to find the square root of a number. This method involves several steps that are repeated to get a more accurate result. Here is a step-by-step guide to finding the square root of 8 using the long division method:
-
Setup: Start by writing the number 8. Place a bar (or overline) over it to indicate that this is the number for which we are finding the square root.
-
Group the Digits: If the number has more digits, pair them from right to left. For 8, since it is a single digit, it remains as it is. For decimal numbers, pair digits to the right of the decimal point.
-
Find the Largest Number: Find the largest number whose square is less than or equal to the number under the bar. For 8, the largest number is 2, because \(2^2 = 4\) which is less than 8.
-
Divide and Subtract: Place 2 as the divisor and the quotient. Subtract the square of the quotient (4) from 8. This gives a remainder of 4.
-
Bring Down Pairs: Bring down pairs of zeros (since there are no more digits in 8) to the right of the remainder. This makes the new dividend 400.
-
Double the Quotient: Double the quotient (which is 2) to get 4. Write it down and leave a blank space next to it. This is our new divisor.
-
Find the New Digit: Find a digit which, when placed next to 4 (making it 40+digit), and multiplied by the same digit, gives a product less than or equal to 400. Here, the digit is 5, because \(45 \times 5 = 225\) which is less than 400.
-
Divide and Subtract Again: Place the digit 5 next to the current quotient, making it 2.5. Subtract 225 from 400, giving a remainder of 175.
-
Repeat the Process: Bring down pairs of zeros again and repeat the steps to continue finding more decimal places. The next steps involve doubling 25 to get 50, finding the next digit, and so on.
By repeating this process, we can get a more precise value for the square root of 8. The approximate value is 2.82842712474619, but the process can be extended for more precision.
The long division method is useful for manual calculations and helps in understanding the concept of square roots and their approximation.
Prime Factorization Method
The Prime Factorization Method is a straightforward way to find the square root of a number by breaking it down into its prime factors. Here is a detailed step-by-step guide to finding the square root of 8 using this method:
-
Prime Factorization:
First, decompose 8 into its prime factors. The number 8 can be written as:
\[ 8 = 2 \times 2 \times 2 \]
-
Grouping the Factors:
Next, group the prime factors into pairs. Since 8 is not a perfect square, we group the factors as much as possible:
\[ \sqrt{8} = \sqrt{2 \times 2 \times 2} \]
We have one complete pair of 2's, and one 2 left over.
-
Simplifying the Expression:
Take one factor from each pair outside the square root sign. For the pair of 2's, this becomes:
\[ \sqrt{2 \times 2 \times 2} = 2\sqrt{2} \]
Thus, the square root of 8 simplifies to:
\[ \sqrt{8} = 2\sqrt{2} \]
To summarize, the prime factorization method involves breaking down the number into its prime factors, grouping them into pairs, and then simplifying the square root expression by taking one factor from each pair outside the square root. This method is particularly useful for understanding the structure of numbers and provides a clear way to handle non-perfect squares.
Using Approximation Techniques
Approximation techniques provide a way to estimate the square root of a number when an exact value is not needed or when a more straightforward calculation is desired. Here are some common methods used to approximate the square root of 8:
1. Linear Approximation
The linear approximation method uses the tangent line to the function at a point close to the value for which we need the square root. For \( \sqrt{8} \), we can use a point near 8, such as 9.
- Identify a close value, \( a \), where \( \sqrt{a} \) is known. Here, \( a = 9 \) and \( \sqrt{9} = 3 \).
- Find the derivative of \( f(x) = \sqrt{x} \) which is \( f'(x) = \frac{1}{2\sqrt{x}} \). At \( x = 9 \), \( f'(9) = \frac{1}{6} \).
- Use the linear approximation formula \( L(x) = f(a) + f'(a)(x - a) \):
\( L(8) = 3 + \frac{1}{6}(8 - 9) = 3 - \frac{1}{6} = 2.8333 \).
Thus, \( \sqrt{8} \approx 2.8333 \).
2. Babylonian (Heron's) Method
This iterative method refines an initial guess to get closer to the actual square root value.
- Choose an initial guess \( x_0 \). For \( \sqrt{8} \), a good starting point is 3.
- Use the formula \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{8}{x_n} \right) \).
- Iterate until the desired accuracy is achieved. For example:
\( x_1 = \frac{1}{2} \left( 3 + \frac{8}{3} \right) = \frac{1}{2} \left( 3 + 2.6667 \right) = 2.8333 \).
\( x_2 = \frac{1}{2} \left( 2.8333 + \frac{8}{2.8333} \right) \approx 2.8284 \).
Thus, \( \sqrt{8} \approx 2.8284 \).
3. Newton-Raphson Method
This method also uses iteration to find successively better approximations.
- Start with an initial guess, say \( x_0 = 3 \).
- Apply the formula \( x_{n+1} = x_n - \frac{x_n^2 - 8}{2x_n} \).
- Iterate until the value stabilizes. For example:
\( x_1 = 3 - \frac{3^2 - 8}{2 \cdot 3} = 3 - \frac{9 - 8}{6} = 2.8333 \).
\( x_2 = 2.8333 - \frac{2.8333^2 - 8}{2 \cdot 2.8333} \approx 2.8284 \).
Thus, \( \sqrt{8} \approx 2.8284 \).
4. Continued Fractions
Continued fractions provide a sequence that converges to the square root.
- The continued fraction for \( \sqrt{8} \) is \( 2 + \frac{1}{1 + \frac{1}{4 + \frac{1}{1 + \frac{1}{4 + \cdots}}}} \).
- Truncating this fraction after a few terms gives an approximation.
- For example, using two terms:
\( 2 + \frac{1}{1 + \frac{1}{4}} = 2 + \frac{1}{1.25} = 2.8 \).
Thus, \( \sqrt{8} \approx 2.8 \).
These techniques allow us to estimate \( \sqrt{8} \) with varying degrees of accuracy, depending on the method and number of iterations used.
Using a Calculator to Find Square Roots
Finding the square root of 8 using a calculator is a straightforward process. Here’s a step-by-step guide to help you:
-
Turn on your calculator:
Ensure your calculator is powered on. For most digital and scientific calculators, there is an "ON" or "C" button to activate it.
-
Locate the square root function:
Look for the square root symbol (√) on your calculator. It might be directly accessible or require pressing a "shift" or "second function" key to access it.
-
Enter the number:
Press the number 8 on your calculator. You should see the number displayed on the screen.
-
Activate the square root function:
Press the square root button (√). On some calculators, you may need to press this button before entering the number. Check your calculator's manual if unsure.
-
Read the result:
The calculator will display the square root of 8. For most calculators, the result will be approximately 2.8284271247461903.
Using a calculator ensures you get a precise and quick result, which is especially useful for more complex numbers that do not have a simple square root.
Step-by-Step Guide to Finding the Square Root of 8
Finding the square root of 8 can be approached through several methods, including manual calculations and using a calculator. Here, we provide a step-by-step guide to manually find the square root of 8 using the long division method.
Step 1: Estimation
Estimate the value of the square root. Since \( \sqrt{9} = 3 \) and \( \sqrt{4} = 2 \), we know that \( \sqrt{8} \) will be between 2 and 3.
Step 2: Setting Up the Long Division
We will use the long division method to find the square root of 8. Follow these steps:
- Write the number 8.000000 with pairs of zeros.
- Starting from the left, find the largest square less than or equal to the first pair or digit. In this case, 22 = 4 is the largest square less than 8.
- Write 2 above the line (quotient) and 4 below 8 (dividend). Subtract 4 from 8 to get 4.
- Bring down the next pair of zeros to make the new dividend 400.
Step 3: Refining the Estimation
Continue the long division steps:
- Double the quotient (2) to get 4, and write it as the new divisor with a blank on its right (4_).
- Find the largest digit (x) to fill the blank such that 4x * x <= 400. Here, 42 * 2 = 84 is the closest without exceeding 400.
- Write 2 next to 2 in the quotient, making it 2.2. Multiply 42 by 2 to get 84 and subtract from 400 to get 316.
- Bring down the next pair of zeros to make the new dividend 31600.
- Double the quotient (22) to get 44, and write it as the new divisor with a blank on its right (44_).
- Find the largest digit (x) to fill the blank such that 44x * x <= 31600. Here, 446 * 6 = 2676 is the closest without exceeding 31600.
- Write 6 next to 2.2 in the quotient, making it 2.82. Multiply 446 by 6 to get 2676 and subtract from 31600 to get 4836.
- Repeat the process to achieve the desired precision. Each step brings down another pair of zeros, and the quotient gets more refined.
Step 4: Finalizing the Result
After several iterations, you will get the square root of 8 to a desired precision. For example, after a few steps, you might find:
2.8284271...
Therefore, the square root of 8 is approximately \( \sqrt{8} \approx 2.828 \).
This step-by-step guide using the long division method helps in understanding how to manually calculate square roots for non-perfect squares like 8.
Step 1: Estimation
Estimating the square root of a number is the first step in finding its accurate value. The process involves identifying two perfect squares between which the given number lies.
For the square root of 8, we follow these steps:
-
Identify Perfect Squares: First, identify the two closest perfect squares around 8. These are 4 (since \(2^2 = 4\)) and 9 (since \(3^2 = 9\)). So, we know that \(2 < \sqrt{8} < 3\).
-
Initial Estimate: Since 8 is closer to 9 than it is to 4, our initial estimate can be slightly less than 3. However, for simplicity, we can start with 3 as a rough estimate.
-
Refine the Estimate: To refine our estimate, we use the average method. Divide 8 by our initial estimate and then average the result with the estimate.
- Divide 8 by 3: \(\frac{8}{3} \approx 2.67\)
- Average the result with 3: \(\frac{2.67 + 3}{2} \approx 2.835\)
-
Repeat if Necessary: To further refine, we repeat the process with the new estimate (2.835).
- Divide 8 by 2.835: \(\frac{8}{2.835} \approx 2.823\)
- Average the result with 2.835: \(\frac{2.823 + 2.835}{2} \approx 2.829\)
-
Final Estimate: After a few iterations, we get a refined estimate close to the actual square root of 8. The more iterations we perform, the closer we get to the precise value, which is approximately 2.828.
This estimation process is essential for understanding how to approach finding square roots manually, even though calculators and other digital tools can provide quick results.
Step 2: Refining the Estimation
After making an initial estimation, refining the estimation involves a few additional steps to get a more accurate value for the square root of 8. One common method to refine the estimation is to use the average of the estimation and the quotient of the number divided by the estimation.
- Let’s assume our initial estimation for the square root of 8 is 2.8.
- Divide 8 by the initial estimation:
\[
\frac{8}{2.8} \approx 2.857
\] - Take the average of the initial estimation and the result from step 2:
\[
\text{New estimation} = \frac{2.8 + 2.857}{2} \approx 2.8285
\] - Check the accuracy by squaring the new estimation:
\[
2.8285^2 \approx 8.0002
\]The result is very close to 8, indicating that 2.8285 is a refined and accurate estimation for the square root of 8.
- If further accuracy is needed, repeat steps 2-4 using the new estimation. For example:
- New estimation: 2.8285
- Divide 8 by the new estimation:
\[
\frac{8}{2.8285} \approx 2.8284
\] - Average of the new estimation and the quotient:
\[
\text{Refined estimation} = \frac{2.8285 + 2.8284}{2} \approx 2.8284
\] - Square the refined estimation:
\[
2.8284^2 \approx 8
\]This confirms the refined estimation as 2.8284, which is a highly accurate value for the square root of 8.
By following these steps, you can continue refining your estimation to achieve the desired level of accuracy for the square root of 8.

Step 3: Verification of Results
After estimating and refining the square root of 8, the next step is to verify the accuracy of our result. Here’s a step-by-step guide to ensure our calculated square root is correct:
-
Square the Result: Take the estimated value of the square root and square it. For example, if our refined estimate is \(2.828\), then:
\[ 2.828 \times 2.828 = 7.991 \]
-
Compare with the Original Number: Compare the squared result with the original number (8 in this case). The closer the squared result is to 8, the more accurate our square root estimate.
-
Use a Tolerance Level: Define an acceptable range of error. For instance, if our squared result falls within 7.999 to 8.001, we can consider our estimate accurate. Given the precision of \(2.828\), the squared value \(7.991\) is close enough to 8, verifying the accuracy of our result.
Let's verify this step-by-step:
- Our refined estimate is \(2.828\).
- Square the estimate: \(2.828 \times 2.828 = 7.991\).
- Since \(7.991\) is very close to \(8\), our estimate is verified as accurate.
Alternatively, you can also use a calculator to directly check the result of \( \sqrt{8} \). A calculator should give you \( \sqrt{8} \approx 2.8284271247461903 \), which reaffirms our manual calculation and verifies our steps.
Using these steps, you can confidently verify the accuracy of your square root calculations.
Common Mistakes to Avoid
When finding the square root of 8, it's essential to be aware of common mistakes that can lead to incorrect results. Here are some frequent errors and tips to avoid them:
-
Incorrect Simplification: It's a common mistake to think that the square root of a sum or product can be simplified directly. For example,
√(a + b) ≠ √a + √band√(a * b) ≠ √a * √b. Always simplify inside the square root first. -
Ignoring the Non-Negative Constraint: The square root function only returns the non-negative root. For example,
√25 = 5, not±5. Ensure to consider only the principal (non-negative) root. -
Incorrectly Handling Radicals: When simplifying radicals, ensure proper factorization. For instance,
√8can be simplified to2√2, not left as√(4*2) = 2√2. Break down the number into its prime factors correctly. -
Misapplying Arithmetic Operations: Avoid adding or subtracting square roots directly unless they have the same radicand. For example,
√8 + √2 ≠ √10. Instead, approximate each square root separately and then add the results. -
Inaccurate Approximation: When approximating square roots manually, ensure to refine your estimation. For instance, estimating
√8might start with2.8, then refine to2.828through iterative methods or using a calculator for precision. -
Forgetting Units in Applied Problems: When applying square roots in geometry or real-life problems, don't forget to include the appropriate units in your final answer. For instance, if calculating the diagonal of a square with side length 8 cm, ensure the final answer includes the unit (e.g.,
2√2 cm).
By being mindful of these common mistakes, you can improve accuracy in calculating square roots and enhance your mathematical problem-solving skills.
Advanced Methods for Finding Square Roots
Finding the square root of a number can be done using various advanced methods. These methods are particularly useful for more precise calculations or when dealing with complex numbers. Here, we explore the Newton-Raphson method and the Babylonian method.
Newton-Raphson Method
The Newton-Raphson method is an iterative numerical technique to find the square root of a number. It converges quickly to the accurate value with successive approximations. Here are the steps:
- Start with an initial guess, \( x_0 \). A good starting point is \( x_0 = \frac{S}{2} \), where \( S \) is the number for which we are finding the square root.
- Use the iteration formula:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right)
\] - Continue iterating until the difference between successive approximations is less than a chosen tolerance level.
For example, to find \(\sqrt{8}\) using this method:
- Initial guess: \( x_0 = \frac{8}{2} = 4 \)
- First iteration: \( x_1 = \frac{1}{2} \left( 4 + \frac{8}{4} \right) = 3 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 3 + \frac{8}{3} \right) \approx 2.8333 \)
- Continue iterations until the value stabilizes around 2.8284.
Babylonian Method (Heron's Method)
The Babylonian method is one of the oldest known algorithms for computing square roots, also known as Heron's method. The process involves a series of refinements based on averaging. Follow these steps:
- Start with an initial guess, \( x_0 \). A typical starting point is \( x_0 = S \), or a close estimate.
- Apply the formula:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right)
\] - Repeat the process until the desired accuracy is achieved.
For \(\sqrt{8}\) using this method:
- Initial guess: \( x_0 = 4 \)
- First iteration: \( x_1 = \frac{1}{2} \left( 4 + \frac{8}{4} \right) = 3 \)
- Second iteration: \( x_2 = \frac{1}{2} \left( 3 + \frac{8}{3} \right) \approx 2.8333 \)
- Continue until the result converges to approximately 2.8284.
Both methods demonstrate how iterative approaches can yield highly accurate results for square roots. For practical purposes, these methods are essential tools in both theoretical mathematics and applied sciences.
Newton-Raphson Method
The Newton-Raphson method is a powerful technique for approximating the square root of a number using calculus. Here's a step-by-step guide on how to use this method to find the square root of 8.
-
Start with an initial guess \( x_0 \). For the square root of 8, a reasonable starting point might be 3 since \( 3^2 = 9 \) is close to 8.
-
Define the function \( f(x) \) and its derivative \( f'(x) \).
- \( f(x) = x^2 - 8 \)
- \( f'(x) = 2x \)
-
Apply the Newton-Raphson formula to get a better approximation:
\( x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \)
-
Iterate this process until the desired accuracy is achieved:
- \( x_1 = 3 - \frac{3^2 - 8}{2 \cdot 3} = 3 - \frac{1}{6} = 2.8333 \)
- \( x_2 = 2.8333 - \frac{2.8333^2 - 8}{2 \cdot 2.8333} \approx 2.8284 \)
- Continue iterating to get more precise results.
After a few iterations, the value will converge to approximately \( 2.8284 \), which is a close approximation of the square root of 8.

Babylonian Method
The Babylonian method, also known as the divide-and-average method, is an ancient algorithm for finding square roots. This method is efficient and converges quickly to the actual square root value. Below is a detailed step-by-step process to find the square root of 8 using the Babylonian method.
-
Initial Guess: Start with an initial guess, \( A_0 \). For the square root of 8, we can choose an initial guess of 3, as it is close to the actual square root.
Initial guess, \( A_0 = 3 \)
-
First Approximation: Use the formula \( A_1 = \frac{A_0 + \frac{N}{A_0}}{2} \), where \( N \) is the number for which we are finding the square root. For \( N = 8 \), calculate:
\( A_1 = \frac{3 + \frac{8}{3}}{2} = \frac{3 + 2.67}{2} = \frac{5.67}{2} \approx 2.835 \)
-
Second Approximation: Use the same formula iteratively with \( A_1 \) to find \( A_2 \):
\( A_2 = \frac{A_1 + \frac{N}{A_1}}{2} = \frac{2.835 + \frac{8}{2.835}}{2} \approx \frac{2.835 + 2.822}{2} \approx 2.828 \)
-
Further Iterations: Continue the iterations until the value stabilizes and the difference between successive approximations becomes negligible:
\( A_3 = \frac{2.828 + \frac{8}{2.828}}{2} \approx 2.828 \)
-
Conclusion: After a few iterations, the approximation stabilizes around \( 2.828 \), which is the square root of 8 to three decimal places.
The Babylonian method is a simple yet powerful technique for finding square roots, demonstrating the ingenuity of ancient mathematical methods that are still relevant today.
Square Roots in Real Life Applications
Square roots play a crucial role in various real-life applications across different fields. Here are some notable examples:
-
Construction and Engineering:
In construction, square roots are used to calculate the length of diagonal braces, ensuring structural integrity. For example, if a builder needs to determine the diagonal length of a rectangular frame, they can use the Pythagorean theorem which involves taking the square root of the sum of the squares of the other two sides.
-
Finance:
Square roots are used to calculate stock market volatility. Investors use the square root of the variance of stock returns to assess the risk associated with an investment.
-
Science:
Square roots are essential in various scientific calculations such as determining the velocity of an object, the intensity of sound waves, or the amount of radiation absorbed by a material. These calculations help scientists understand natural phenomena and develop new technologies.
-
Statistics:
In statistical analysis, square roots are used to calculate the standard deviation, which is the square root of the variance. This metric helps statisticians understand the spread of data points around the mean.
-
Geometry:
Square roots are frequently used in geometry to solve problems involving right triangles. For instance, the Pythagorean theorem, which is used to find the length of a triangle's hypotenuse, relies on calculating the square root of the sum of the squares of the other two sides.
-
Computer Science:
In computer science, square roots are used in algorithms for encryption, image processing, and game physics. For example, calculating the distance between two points in a digital image or in a game environment involves the use of square roots.
-
Navigation:
Square roots are used in navigation to determine the distance between two points on a map. For example, the distance formula, which calculates the distance between two points in a coordinate plane, uses square roots to find the direct distance.
These examples demonstrate the versatility and importance of square roots in practical applications, highlighting their relevance in everyday life as well as in professional fields.
Xem video hướng dẫn cách đơn giản hóa căn bậc hai của số 8 (sqrt(8)).
Video: Cách đơn giản hóa căn bậc hai của 8: sqrt(8)
READ MORE:
Xem video hướng dẫn cách tính căn bậc hai của số 8.
Video: Cách tính căn bậc hai của số 8