Topic square root of negative 1 divided by 8: Understanding the square root of negative 1 divided by 8 involves delving into complex numbers and their applications. This concept, often represented as a fraction with an imaginary unit, plays a crucial role in advanced mathematics and engineering. In this article, we explore the fundamentals, calculations, and implications of this mathematical expression.
Table of Content
- Understanding the Square Root of a Negative Number Divided by 8
- Introduction to Square Roots
- Mathematical Background
- Square Roots of Positive Numbers
- Square Roots of Negative Numbers
- Complex Numbers and Imaginary Units
- Calculating Square Roots Manually
- Using Square Root Calculators
- Examples and Practice Problems
- Simplifying Radical Expressions
- Applications of Square Roots
- Advanced Topics
- Online Tools and Resources
- YOUTUBE: Xem video giải thích vì sao căn bậc hai của số âm một bằng số phức i trong toán học, bao gồm lý do và các ứng dụng của nó.
Understanding the Square Root of a Negative Number Divided by 8
The mathematical expression for the square root of a negative number divided by 8 can be analyzed using complex numbers. The square root of -1 is represented by the imaginary unit \( i \). Therefore, the expression can be written as:
\[
\frac{\sqrt{-1}}{8} = \frac{i}{8}
\]
This simplifies to:
\[
\frac{i}{8} = 0.125i
\]
Steps to Calculate
- Identify the square root of -1 as \( i \).
- Divide \( i \) by 8 to get the final result.
Applications in Mathematics
Complex numbers are used in various fields such as engineering, physics, and applied mathematics. Understanding how to manipulate and use imaginary numbers is crucial for solving advanced problems in these areas.
Tools for Calculation
Several online calculators can help you perform such calculations:

READ MORE:
Introduction to Square Roots
The concept of a square root involves finding a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because \(3 \times 3 = 9\). The square root function is denoted using the radical symbol (√), such as \(\sqrt{9} = 3\).
Square roots apply to both positive and negative numbers, although the square roots of negative numbers introduce the concept of complex numbers. For example, the square root of -1 is represented by the imaginary unit \(i\), where \(i^2 = -1\). Thus, the square root of -8 can be expressed as \(\sqrt{-8} = \sqrt{8} \cdot \sqrt{-1} = 2\sqrt{2}i\).
Here is a step-by-step guide to understanding square roots:
- Positive Numbers: The square root of a positive number \(a\) is a number \(b\) such that \(b^2 = a\). For instance, \(\sqrt{25} = 5\) because \(5 \times 5 = 25\).
- Zero: The square root of zero is zero, \(\sqrt{0} = 0\), because \(0 \times 0 = 0\).
- Negative Numbers: The square root of a negative number involves the imaginary unit \(i\). For example, \(\sqrt{-9} = 3i\), since \((3i) \times (3i) = 9i^2 = -9\).
Let's explore a more complex example:
-
Example: Simplifying \(\sqrt{-1/8}\):
- First, express \(\sqrt{-1/8}\) as \(\sqrt{\frac{-1}{8}}\).
- Next, separate the square root of the fraction: \(\sqrt{\frac{-1}{8}} = \frac{\sqrt{-1}}{\sqrt{8}}\).
- Recognize that \(\sqrt{-1} = i\), thus \(\frac{i}{\sqrt{8}}\).
- Finally, simplify the expression to \(\frac{i}{2\sqrt{2}}\). Rationalize the denominator by multiplying by \(\sqrt{2}/\sqrt{2}\), resulting in \(\frac{i \sqrt{2}}{4}\).
In summary, understanding square roots, especially those involving negative numbers, requires a grasp of both real and complex numbers. Calculators and tools can assist in finding square roots, but the foundational knowledge of the principles behind these operations is crucial for a comprehensive understanding.
Mathematical Background
The mathematical concept of square roots is fundamental in understanding various aspects of algebra and complex numbers. The square root of a number \( x \) is a value \( y \) such that \( y^2 = x \). This is typically denoted as \( \sqrt{x} \).
Square Roots of Positive Numbers
For any positive number, there are two square roots: one positive and one negative. For example:
- \(\sqrt{9} = 3\) and \(\sqrt{9} = -3\)
However, the principal square root is the positive one, usually denoted simply as \( \sqrt{9} = 3 \).
Square Roots of Negative Numbers
The square roots of negative numbers involve imaginary numbers, denoted by \( i \), where \( i = \sqrt{-1} \). For example:
- \(\sqrt{-9} = \sqrt{9 \cdot (-1)} = \sqrt{9} \cdot \sqrt{-1} = 3i\)
Example: Square Root of -1/8
Let's consider the square root of \(\frac{-1}{8}\). This can be calculated as follows:
- \(\sqrt{\frac{-1}{8}} = \sqrt{\frac{1}{8} \cdot -1} = \sqrt{\frac{1}{8}} \cdot \sqrt{-1}\)
- \(\sqrt{\frac{1}{8}} = \frac{1}{\sqrt{8}} = \frac{\sqrt{8}}{8} = \frac{\sqrt{4 \cdot 2}}{8} = \frac{2\sqrt{2}}{8} = \frac{\sqrt{2}}{4}\)
- Thus, \(\sqrt{\frac{-1}{8}} = \frac{\sqrt{2}}{4} \cdot i = \frac{\sqrt{2}i}{4}\)
Simplifying Radical Expressions
Simplifying square roots involves expressing the number inside the square root in its simplest form. For example:
- \(\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}\)
Properties and Rules
- For any non-negative numbers \(a\) and \(b\): \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)
- For any non-negative numbers \(a\) and \(b\): \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
Understanding these fundamental properties of square roots is crucial in higher mathematics, particularly in solving quadratic equations and working with complex numbers. Imaginary numbers, represented as multiples of \(i\), play a significant role in extending the concept of square roots to negative numbers, providing solutions that were previously considered impossible.
Square Roots of Positive Numbers
The square root of a positive number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\). Similarly, the square root of 16 is 4 because \(4 \times 4 = 16\).
Square roots are denoted by the radical symbol \( \sqrt{} \). The principal (positive) square root of a number \(a\) is written as \( \sqrt{a} \). Here are some properties and examples to help understand square roots of positive numbers:
- The square root of 0 is 0: \( \sqrt{0} = 0 \).
- The square root of 1 is 1: \( \sqrt{1} = 1 \).
- The square root of a positive number greater than 1 is also a positive number less than the original number (except for perfect squares):
For instance:
| \( \sqrt{4} \) | = 2 |
| \( \sqrt{9} \) | = 3 |
| \( \sqrt{25} \) | = 5 |
| \( \sqrt{2} \) | \(\approx 1.414\) |
| \( \sqrt{10} \) | \(\approx 3.162\) |
Using a calculator, you can find the square root of any positive number easily. For example, to find the square root of 2, enter 2 and then press the square root function key (√), and you should get approximately 1.414213562.
There are some rules and properties associated with square roots:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
In addition, the principal square root is always non-negative, even though there are technically two square roots for any positive number, one positive and one negative. For example, \( \sqrt{16} = 4 \) and \( -\sqrt{16} = -4 \).
Understanding square roots is fundamental in various fields of mathematics, including algebra, geometry, and calculus, as well as in practical applications such as physics and engineering.
Square Roots of Negative Numbers
Square roots of negative numbers introduce the concept of imaginary numbers. While the square root of a positive number is always a real number, the square root of a negative number is imaginary. The imaginary unit is denoted as \( i \), where \( i \) is defined as the square root of -1:
\[ i = \sqrt{-1} \]
Using this definition, we can express the square root of any negative number. For a negative number \(-x\), where \( x \) is positive, the square root can be written as:
\[ \sqrt{-x} = \sqrt{(-1) \cdot x} = \sqrt{-1} \cdot \sqrt{x} = i \sqrt{x} \]
Let's go through a few examples to illustrate this:
- Example 1: Find the square root of -25.
\[ \sqrt{-25} = \sqrt{(-1) \cdot 25} = \sqrt{-1} \cdot \sqrt{25} = i \cdot 5 = 5i \]
- Example 2: Find the square root of -81.
\[ \sqrt{-81} = \sqrt{(-1) \cdot 81} = \sqrt{-1} \cdot \sqrt{81} = i \cdot 9 = 9i \]
- Example 3: Find the square root of -3.
\[ \sqrt{-3} = \sqrt{(-1) \cdot 3} = \sqrt{-1} \cdot \sqrt{3} = i \cdot \sqrt{3} \approx 1.732i \]
These examples show that the square root of a negative number always involves the imaginary unit \( i \). Understanding this concept is crucial for working with complex numbers, which are used extensively in advanced mathematics and engineering.

Complex Numbers and Imaginary Units
Complex numbers extend the idea of one-dimensional number lines to two dimensions by incorporating an imaginary unit, \( i \), defined by the property \( i^2 = -1 \). This allows for the expression of numbers that are not real.
A complex number is generally written in the form \( a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit. Here, \( a \) is known as the real part, and \( b \) is the imaginary part of the complex number.
Properties of the Imaginary Unit
- \( i = \sqrt{-1} \)
- \( i^2 = -1 \)
- \( i^3 = -i \)
- \( i^4 = 1 \)
Calculating the Square Root of a Negative Number
To find the square root of a negative number, we utilize the imaginary unit \( i \). For instance, the square root of \(-1\) is \( i \). Similarly, the square root of \(-8\) can be determined as follows:
Given the expression \(\sqrt{-8}\), we can rewrite it using the properties of \( i \):
\[
\sqrt{-8} = \sqrt{8 \cdot -1} = \sqrt{8} \cdot \sqrt{-1} = \sqrt{8} \cdot i = 2\sqrt{2} \cdot i = 2i\sqrt{2}
\]
Square Roots of Complex Numbers
To find the square root of a complex number, we use the formula:
\[
\sqrt{a + bi} = c + di
\]
Where:
- \( c = \frac{1}{\sqrt{2}} \sqrt{ \sqrt{a^2 + b^2} + a } \)
- \( d = \frac{\text{sign}(b)}{\sqrt{2}} \sqrt{ \sqrt{a^2 + b^2} - a } \)
For example, the square root of \( 3 - 5i \) is calculated as:
\[
c = \frac{1}{\sqrt{2}} \sqrt{ \sqrt{3^2 + (-5)^2} + 3 } = 2.1013034
\]
\[
d = \frac{-1}{\sqrt{2}} \sqrt{ \sqrt{3^2 + (-5)^2} - 3 } = -1.1897378
\]
\]
Thus, the square root of \( 3 - 5i \) is approximately \( 2.1013034 - 1.1897378i \).
Calculating Square Roots Manually
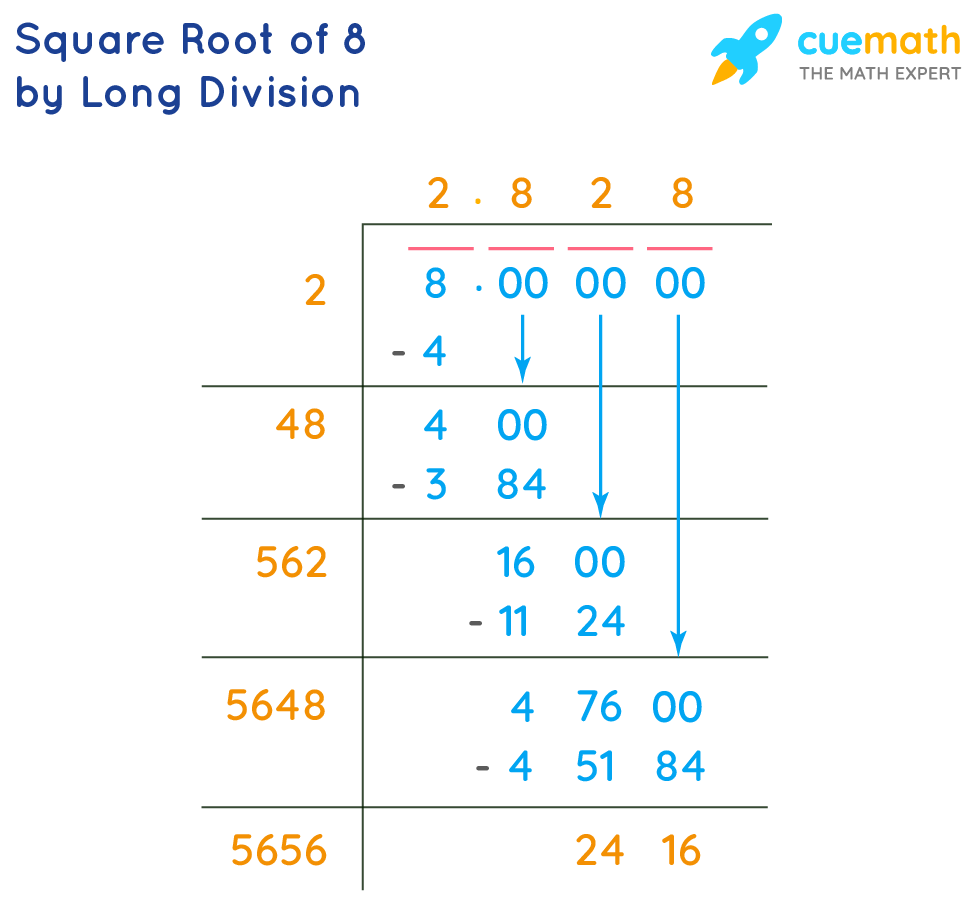
Calculating square roots manually involves several steps. Here's a detailed, step-by-step guide:
-
Estimate the Square Root:
Begin by finding two perfect squares between which your number lies. For example, if you want to find the square root of 50, you know that \(7^2 = 49\) and \(8^2 = 64\). Therefore, the square root of 50 is between 7 and 8.
-
Divide and Average Method:
-
Choose a number as your initial guess. Let's start with 7.5 for \(\sqrt{50}\).
-
Divide the number you want the square root of by your guess: \(\frac{50}{7.5} = 6.67\).
-
Average the result with your guess: \(\frac{7.5 + 6.67}{2} = 7.085\).
-
Repeat the process with the new guess: \(\frac{50}{7.085} \approx 7.06\).
-
Continue this process until the results converge to a stable value. This will be your estimated square root.
-
-
Using the Long Division Method:
-
Write the number in pairs of digits from the decimal point. For 50, it’s written as 50.00.
-
Find the largest number whose square is less than or equal to the first pair. For 50, this number is 7 because \(7^2 = 49\).
-
Subtract the square from the first pair and bring down the next pair: \(50 - 49 = 1\). Bring down 00 to get 100.
-
Double the divisor (which is 7), giving 14. Determine the next digit by finding the largest digit x such that \(14x \times x \leq 100\). Here, x is 7 because \(147 \times 7 = 1029\), which is close but over, so x is 6.
-
Continue this process to find more decimal places as needed.
-
-
Using Prime Factorization:
-
Find the prime factors of the number. For example, the prime factors of 50 are \(2 \times 5^2\).
-
Pair the prime factors and simplify: \( \sqrt{50} = \sqrt{2 \times 5^2} = 5 \sqrt{2}\).
-
These methods provide different approaches to manually calculating square roots, each useful in different contexts. Understanding these can deepen your mathematical knowledge and enhance your problem-solving skills.
Using Square Root Calculators
Square root calculators are useful tools for quickly determining the square root of a given number, including complex and imaginary numbers. They are especially handy for solving problems that involve roots of negative numbers or fractions. Here’s a step-by-step guide on how to use them effectively:
-
Access a Square Root Calculator: There are many online square root calculators available, such as those on , , and .
-
Input the Number: Enter the number you want to find the square root of. For example, to find the square root of -1/8, input -1/8 into the calculator.
-
Calculate: Press the calculate button. The calculator will process the input and display the result. For the square root of -1/8, the result will include the imaginary unit i since the square root of a negative number is not a real number.
\[\sqrt{\frac{-1}{8}} = \frac{\sqrt{-1}}{\sqrt{8}} = \frac{i}{2\sqrt{2}} = \frac{i\sqrt{2}}{4}\]
-
Interpret the Result: The calculator will provide the result in both exact and decimal forms. For the example above, it will show \(\frac{i\sqrt{2}}{4}\) and its decimal approximation.
Using these calculators can save time and reduce errors when performing complex calculations manually. They are also helpful for learning and verifying the steps involved in solving square roots of various numbers.
Examples and Practice Problems
Understanding the square root of negative numbers and their applications in complex numbers is crucial. Below are some examples and practice problems to help solidify these concepts.
Example 1: Basic Square Root Calculation
Calculate the square root of -1 divided by 8.
- Step 1: Understand that the square root of -1 is represented by the imaginary unit \( i \).
- Step 2: Express the problem as \( \sqrt{\frac{-1}{8}} \).
- Step 3: Rewrite it using the property of square roots: \( \sqrt{\frac{-1}{8}} = \frac{\sqrt{-1}}{\sqrt{8}} \).
- Step 4: Substitute \( i \) for \( \sqrt{-1} \): \( \frac{i}{\sqrt{8}} \).
- Step 5: Simplify \( \sqrt{8} \) to \( 2\sqrt{2} \): \( \frac{i}{2\sqrt{2}} \).
- Step 6: Rationalize the denominator: \( \frac{i \sqrt{2}}{4} \).
Thus, \( \sqrt{\frac{-1}{8}} = \frac{i \sqrt{2}}{4} \).
Practice Problems
- Calculate \( \sqrt{-16} \).
- Solution: Recognize that \( \sqrt{-16} = \sqrt{16 \cdot -1} = \sqrt{16} \cdot \sqrt{-1} = 4i \).
- Find the square root of -25 divided by 9.
- Solution: \( \sqrt{\frac{-25}{9}} = \frac{\sqrt{-25}}{\sqrt{9}} = \frac{5i}{3} \).
- Simplify \( \sqrt{-9 \cdot -4} \).
- Solution: \( \sqrt{(-9) \cdot (-4)} = \sqrt{36} = 6 \).
Additional Exercises
To further practice, try these problems:
- Simplify \( \sqrt{\frac{-36}{49}} \).
- Calculate \( \sqrt{-81} \) and express the answer in terms of \( i \).
- Solve \( \sqrt{\frac{-4}{25}} \).
Working through these examples and practice problems will help you become more comfortable with square roots of negative numbers and their representations using imaginary units.

Simplifying Radical Expressions
Radical expressions often need to be simplified to their simplest form for ease of calculation and understanding. Simplifying radicals involves several steps, which include factoring, reducing, and rationalizing the denominator if necessary.
Steps to Simplify Radical Expressions
-
Factor the Radicand: Break down the number inside the radical into its prime factors.
Example: Simplify \(\sqrt{50}\)
- Factor 50 into prime factors: \(50 = 2 \times 5^2\)
- Rewrite the radical expression: \(\sqrt{50} = \sqrt{2 \times 5^2}\)
-
Separate the Radical: Use the property of square roots to separate the factors.
Example: \(\sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2}\)
-
Simplify Each Radical: Simplify the radicals where possible.
Example: \(\sqrt{5^2} = 5\), so \(\sqrt{2} \times \sqrt{5^2} = \sqrt{2} \times 5 = 5\sqrt{2}\)
-
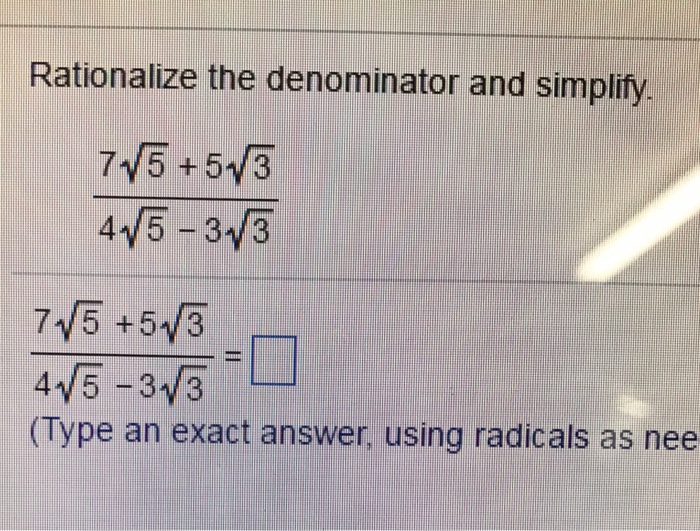
Rationalize the Denominator (if necessary): If the radical expression is a fraction with a radical in the denominator, multiply the numerator and denominator by a radical that will make the denominator a whole number.
Example: Simplify \(\frac{1}{\sqrt{2}}\)
- Multiply the numerator and denominator by \(\sqrt{2}\): \(\frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} = \frac{\sqrt{2}}{2}\)
Examples of Simplified Radical Expressions
- \(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\)
- \(\sqrt{72} = \sqrt{2^3 \times 3^2} = 6\sqrt{2}\)
- \(\frac{\sqrt{50}}{\sqrt{2}} = \frac{5\sqrt{2}}{\sqrt{2}} = 5\)
Practice Problems
- Simplify \(\sqrt{75}\)
- Simplify \(\frac{1}{\sqrt{5}}\)
- Simplify \(\sqrt{32}\)
- Simplify \(\frac{\sqrt{18}}{\sqrt{3}}\)
These steps and examples should help in understanding how to simplify radical expressions effectively. Regular practice with different problems will enhance your skills in this area.
Applications of Square Roots
Square roots have numerous applications across various fields, including mathematics, science, engineering, and everyday life. Here, we will explore some key applications:
- Geometry: Square roots are used to calculate the lengths of sides in right triangles through the Pythagorean theorem. For a right triangle with sides \(a\) and \(b\), and hypotenuse \(c\), the relationship is \(c = \sqrt{a^2 + b^2}\).
- Physics: In physics, square roots are often found in formulas related to wave functions, energy, and kinematics. For example, the formula for the period of a pendulum \(T\) is \(T = 2\pi \sqrt{\frac{L}{g}}\), where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity.
- Engineering: Engineers use square roots in various calculations, such as determining the RMS (root mean square) value of electrical currents and voltages, which is crucial in AC circuit analysis.
- Statistics: In statistics, the standard deviation, a measure of the amount of variation or dispersion in a set of values, is calculated using the square root of the variance.
- Finance: Square roots are used in finance to calculate the volatility of stock prices. The standard deviation of returns is derived using the square root of the variance of returns.
- Everyday Life: Square roots are used in everyday scenarios such as calculating areas and diagonals of squares and rectangles, converting units of measurement, and solving practical problems involving quadratic equations.
Let's look at a few practical examples:
- Example 1:
Find the diagonal of a square with side length 5 units.
The diagonal \(d\) can be found using the formula \(d = \sqrt{a^2 + a^2} = a\sqrt{2}\).
Substituting \(a = 5\), we get \(d = 5\sqrt{2} \approx 7.07\) units. - Example 2:
Calculate the standard deviation of the set {2, 4, 4, 4, 5, 5, 7, 9}.
First, find the mean: \(\bar{x} = \frac{2 + 4 + 4 + 4 + 5 + 5 + 7 + 9}{8} = 5\).
Then, find the variance: \(\sigma^2 = \frac{\sum (x_i - \bar{x})^2}{N} = \frac{(2-5)^2 + (4-5)^2 + (4-5)^2 + (4-5)^2 + (5-5)^2 + (5-5)^2 + (7-5)^2 + (9-5)^2}{8} = 4\).
Finally, take the square root of the variance: \(\sigma = \sqrt{4} = 2\).
These examples illustrate how square roots are an integral part of various calculations and problem-solving techniques.
Advanced Topics
One of the intriguing topics in mathematics involves understanding complex numbers and imaginary units. Let's delve into a specific example related to the complex number \( i \), where \( i \) represents the square root of negative 1.
To explore further, consider the expression \( \frac{i}{8} \). To simplify this, we proceed as follows:
- Recognize that \( i \) is defined as \( \sqrt{-1} \).
- Multiply both numerator and denominator by \( i \) to eliminate the denominator: \[ \frac{i}{8} = \frac{i \cdot i}{8 \cdot i} = \frac{i^2}{8i}. \]
- Since \( i^2 = -1 \), substitute this value: \[ \frac{i^2}{8i} = \frac{-1}{8i}. \]
- To express \( \frac{-1}{8i} \) in a more standard form, multiply numerator and denominator by \( i \): \[ \frac{-1}{8i} = \frac{-1 \cdot i}{8i \cdot i} = \frac{-i}{8i^2}. \]
- Given \( i^2 = -1 \), substitute: \[ \frac{-i}{8i^2} = \frac{-i}{8(-1)} = \frac{-i}{-8} = \frac{i}{8}. \]
Therefore, \( \frac{i}{8} \) simplifies to \( \frac{i}{8} \).
Online Tools and Resources
When exploring mathematical concepts like the square root of negative 1 divided by 8, it's beneficial to utilize online tools and resources that can provide clarity and computational assistance. Below are some recommended tools:
- : A computational knowledge engine that can compute complex mathematical expressions and provide step-by-step solutions.
- : An advanced math solver that can handle various mathematical problems, including complex numbers and fractions.
- : A problem-solving tool that covers a wide range of mathematical topics, offering detailed solutions and explanations.
These tools can enhance understanding and facilitate learning by providing instant solutions and detailed explanations for complex mathematical expressions and operations.

Xem video giải thích vì sao căn bậc hai của số âm một bằng số phức i trong toán học, bao gồm lý do và các ứng dụng của nó.
Tại sao căn bậc hai của số âm một bằng i?
READ MORE:
Xem video giải thích về lý do tại sao
Tại sao "x mũ một nửa" có nghĩa là căn bậc hai?