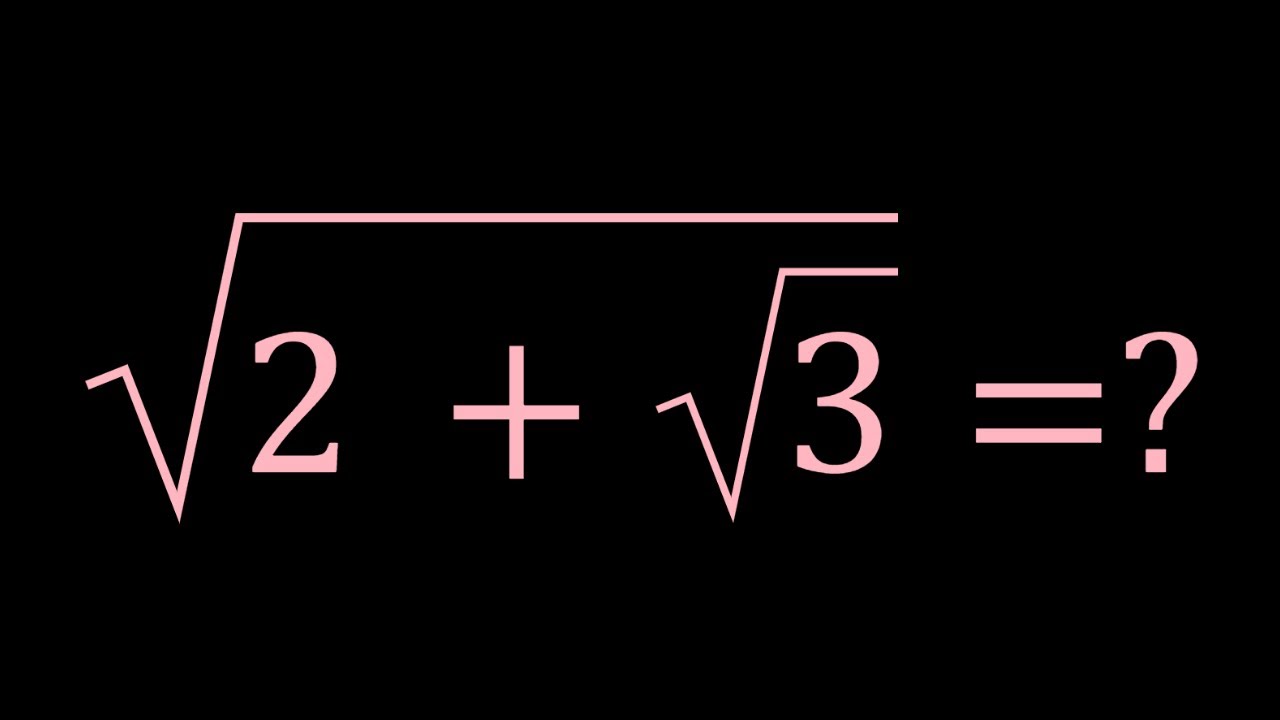Topic 2 square root of 7: Discover the intriguing world of the mathematical expression 2 square root of 7. This article delves into its calculation, properties, and real-world applications, offering a comprehensive understanding that will enhance your appreciation of its significance in various mathematical contexts. Join us on this enlightening journey!
Table of Content
- Understanding the Expression: \(2\sqrt{7}\)
- Introduction to 2 Square Root of 7
- Understanding the Square Root Concept
- Mathematical Calculation of 2 Square Root of 7
- Properties of Square Roots
- Applications of 2 Square Root of 7
- 2 Square Root of 7 in Geometry
- 2 Square Root of 7 in Algebra
- 2 Square Root of 7 in Trigonometry
- Visualizing 2 Square Root of 7
- Historical Context of Square Roots
- Advanced Mathematical Proofs Involving 2 Square Root of 7
- Common Misconceptions About Square Roots
- Real-World Examples of 2 Square Root of 7
- Further Reading and Resources
- YOUTUBE: Tìm hiểu về căn bậc hai cùng thầy J trong video này. Hiểu rõ khái niệm và cách áp dụng căn bậc hai vào các bài toán thực tế.
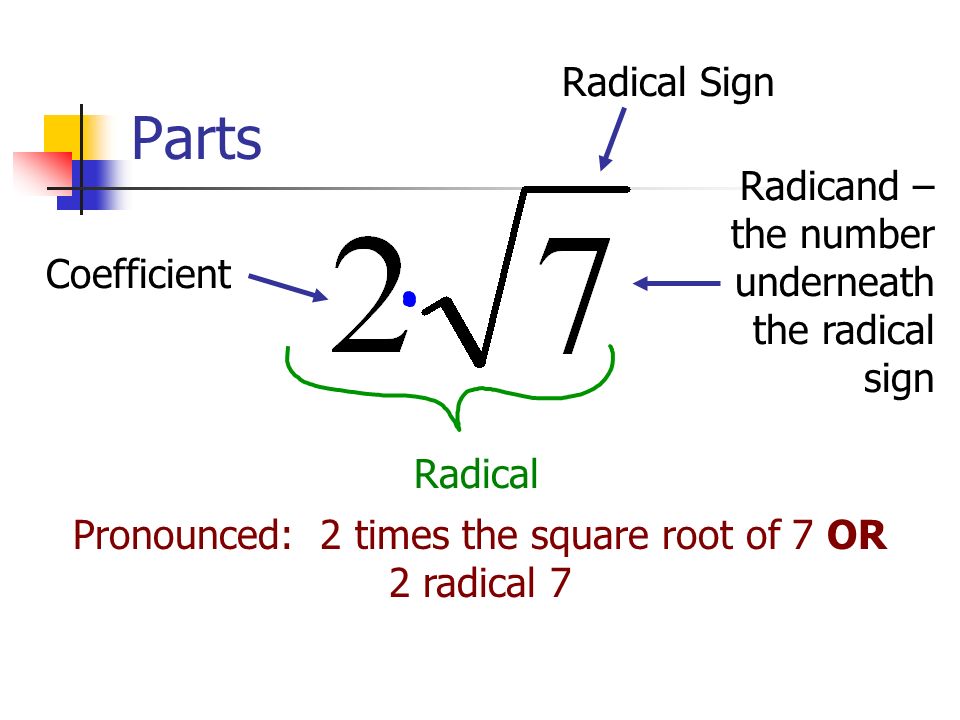
Understanding the Expression: \(2\sqrt{7}\)
The expression \(2\sqrt{7}\) combines a constant with an irrational number. Let's break it down:
Breaking Down the Expression
- \(\sqrt{7}\): This represents the square root of 7. The square root of a number \(x\) is a value that, when multiplied by itself, gives \(x\). For 7, \(\sqrt{7}\) is an irrational number, approximately equal to 2.64575.
- 2: This is a constant multiplier. When we multiply a constant by an irrational number, the result is also an irrational number.
Calculating \(2\sqrt{7}\)
To find the numerical value of \(2\sqrt{7}\), we multiply 2 by the square root of 7:
\[
2\sqrt{7} = 2 \times \sqrt{7} \approx 2 \times 2.64575 = 5.2915
\]
Properties and Applications
Understanding the expression \(2\sqrt{7}\) is important in various mathematical contexts, including:
- Geometry: It may represent lengths, areas, or other measurements involving the square root of 7.
- Algebra: It appears in equations and expressions that require manipulation of radicals.
- Trigonometry: In certain cases, it can be part of trigonometric identities or solutions.
Visual Representation
If we were to plot \(y = 2\sqrt{7}\) on a graph, it would be a horizontal line at \(y \approx 5.2915\), as it is a constant value.
Further Exploration
For those interested in deeper mathematical concepts, consider exploring the following:
- Proofs involving irrational numbers
- Properties of square roots
- Applications in higher mathematics and physics
The expression \(2\sqrt{7}\) may seem simple, but it holds significant importance in various areas of mathematics and science, illustrating the beauty and complexity of irrational numbers and their applications.

READ MORE:
Introduction to 2 Square Root of 7
The expression \(2\sqrt{7}\) is a mathematical term combining a constant and an irrational number. To understand this expression fully, we need to break it down step by step:
-
Understanding Square Roots:
The square root of a number \(x\) is a value that, when multiplied by itself, equals \(x\). For example, the square root of 7 is written as \(\sqrt{7}\), which is approximately 2.64575.
-
Combining with Constants:
In the expression \(2\sqrt{7}\), the number 2 is a constant multiplier. Multiplying a constant by an irrational number yields another irrational number.
-
Calculation:
To find the numerical value of \(2\sqrt{7}\), perform the multiplication:
\[
2\sqrt{7} = 2 \times \sqrt{7} \approx 2 \times 2.64575 = 5.2915
\] -
Properties and Importance:
- Geometry: The expression can represent lengths, areas, or other geometric measurements.
- Algebra: It appears in equations and can be simplified or manipulated in various ways.
- Trigonometry: It is used in trigonometric identities and calculations.
Understanding \(2\sqrt{7}\) provides insight into how constants and irrational numbers interact, revealing the richness of mathematical expressions and their applications across different fields.
Understanding the Square Root Concept
The square root is a fundamental concept in mathematics, essential for solving various equations and understanding geometric properties. Here's a detailed explanation of the square root concept:
-
Definition of Square Root:
The square root of a number \(x\) is a value \(y\) such that \(y^2 = x\). This is written mathematically as \(\sqrt{x} = y\). For example, the square root of 16 is 4 because \(4^2 = 16\).
-
Square Root of Non-Perfect Squares:
Not all numbers have integer square roots. For instance, \(\sqrt{7}\) is not an integer and is approximately 2.64575. These numbers are called irrational numbers.
-
Properties of Square Roots:
- Non-negativity: The square root of a non-negative number is also non-negative. \(\sqrt{x} \geq 0\) for \(x \geq 0\).
- Multiplication: The square root of a product is the product of the square roots. \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).
- Division: The square root of a quotient is the quotient of the square roots. \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \(b \ne 0\).
-
Visual Representation:
Square roots can be visualized geometrically. For instance, if a square has an area of \(x\) square units, the length of each side of the square is \(\sqrt{x}\) units.
-
Applications of Square Roots:
- Geometry: Calculating side lengths, areas, and diagonals.
- Algebra: Solving quadratic equations and simplifying expressions.
- Trigonometry: Appears in various trigonometric identities and formulas.
Understanding the concept of square roots is crucial for delving deeper into more advanced mathematical topics and solving practical problems in science and engineering.
Mathematical Calculation of 2 Square Root of 7
The expression \(2\sqrt{7}\) involves both multiplication and the square root operation. Here's a step-by-step guide to calculating this value:
-
Understanding the Components:
- \(2\): A constant multiplier.
- \(\sqrt{7}\): The square root of 7, an irrational number approximately equal to 2.64575.
-
Calculation of Square Root:
The square root of 7 can be estimated or found using a calculator:
\[
\sqrt{7} \approx 2.64575
\] -
Multiplication:
Next, multiply the constant 2 by the approximate value of \(\sqrt{7}\):
\[
2 \times \sqrt{7} \approx 2 \times 2.64575
\]Performing the multiplication gives:
\[
2 \times 2.64575 = 5.2915
\] -
Exact Form:
While 5.2915 is a useful decimal approximation, the exact form of the expression remains \(2\sqrt{7}\). This form is often preferred in mathematical contexts where precision is crucial.
-
Applications and Usage:
- Geometry: Used to express lengths and areas involving \(\sqrt{7}\).
- Algebra: Appears in equations and simplifications requiring exact forms.
- Physics and Engineering: Represents quantities in scientific calculations.
The calculation of \(2\sqrt{7}\) illustrates the process of combining constants with irrational numbers, showcasing the beauty and complexity of mathematical expressions.
Properties of Square Roots
The square root function has several important properties that are fundamental in mathematics. These properties help in simplifying expressions and solving equations. Here are the key properties of square roots:
-
Non-negativity:
The square root of a non-negative number is always non-negative. This means \(\sqrt{x} \geq 0\) for any \(x \geq 0\).
-
Product Property:
The square root of a product is the product of the square roots. For any non-negative numbers \(a\) and \(b\):
\[
\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}
\] -
Quotient Property:
The square root of a quotient is the quotient of the square roots. For any non-negative numbers \(a\) and \(b\) (with \(b \ne 0\)):
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\] -
Square of a Square Root:
The square of the square root of a number returns the original number. For any non-negative number \(x\):
\[
(\sqrt{x})^2 = x
\] -
Addition and Subtraction:
Square roots do not distribute over addition or subtraction. This means:
\[
\sqrt{a + b} \ne \sqrt{a} + \sqrt{b}
\]
\[
\sqrt{a - b} \ne \sqrt{a} - \sqrt{b}
\] -
Rationalizing the Denominator:
When a square root appears in the denominator, it is often useful to rationalize the denominator. For example:
\[
\frac{1}{\sqrt{a}} = \frac{\sqrt{a}}{a}
\] -
Complex Numbers:
The square root of a negative number involves complex numbers. For example, \(\sqrt{-1} = i\), where \(i\) is the imaginary unit.
These properties of square roots are essential tools in algebra, calculus, and many areas of applied mathematics, enabling us to manipulate and simplify expressions effectively.
Applications of 2 Square Root of 7
The expression \(2\sqrt{7}\) is not just a mathematical curiosity but finds applications in various fields. Here are some of the key areas where \(2\sqrt{7}\) is useful:
-
Geometry:
Lengths and Distances: In geometry, expressions involving square roots are common when calculating lengths and distances. For instance, \(2\sqrt{7}\) can represent the length of the diagonal of a rectangle or a distance in a coordinate plane.
Areas: Certain areas in geometric figures can be expressed using square roots, especially when dealing with right triangles or circles.
-
Algebra:
Simplification: Algebraic expressions often involve square roots. Simplifying and solving equations can require manipulating terms like \(2\sqrt{7}\).
Quadratic Equations: Solutions to quadratic equations can involve square roots, and expressions like \(2\sqrt{7}\) may appear in the solutions.
-
Trigonometry:
Trigonometric Identities: Square roots are prevalent in trigonometric identities. For example, the Pythagorean identity can involve terms like \(2\sqrt{7}\).
Lengths of Sides in Triangles: In right-angled triangles, the lengths of the sides can be expressed using square roots, particularly when using the Pythagorean theorem.
-
Physics and Engineering:
Wave Equations: Square roots often appear in solutions to wave equations in physics, where expressions like \(2\sqrt{7}\) may describe certain properties of waves.
Engineering Calculations: Many engineering problems involve square roots, from calculating stresses and strains to electrical circuit analysis.
-
Computer Science:
Algorithms: Certain algorithms, especially those involving graphics and spatial calculations, utilize square roots. An expression like \(2\sqrt{7}\) might appear in optimization problems or distance calculations.
In summary, \(2\sqrt{7}\) is more than a mere mathematical expression; it has practical applications in various fields, enhancing our understanding and problem-solving capabilities across disciplines.
2 Square Root of 7 in Geometry
The expression \(2\sqrt{7}\) plays a significant role in various geometric contexts. Here’s a detailed look at its applications in geometry:
-
Diagonal of a Rectangle:
In a rectangle with sides of lengths \(a\) and \(b\), the diagonal \(d\) can be found using the Pythagorean theorem:
\[
d = \sqrt{a^2 + b^2}
\]If \(a = 2\sqrt{7}\) and \(b\) is another known length, the diagonal can be calculated accordingly.
-
Distance in the Coordinate Plane:
The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in the coordinate plane is given by:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]If the difference in coordinates results in a term involving \(\sqrt{7}\), the distance can be simplified to include \(2\sqrt{7}\).
-
Area of a Right Triangle:
In a right triangle with legs of lengths \(a\) and \(b\), the hypotenuse \(c\) can be found using the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]If one leg is \(2\sqrt{7}\), this value directly impacts the calculation of the hypotenuse and the area of the triangle:
\[
\text{Area} = \frac{1}{2}ab
\] -
Circle Properties:
The radius of a circle can sometimes be expressed using square roots. For example, if the radius is \(2\sqrt{7}\), the area \(A\) and circumference \(C\) of the circle are calculated as:
\[
A = \pi (2\sqrt{7})^2 = 28\pi
\]
\[
C = 2\pi (2\sqrt{7}) = 4\pi\sqrt{7}
\] -
Volumes and Surface Areas:
In three-dimensional geometry, expressions like \(2\sqrt{7}\) can appear in formulas for volumes and surface areas of solids. For example, the diagonal of a rectangular prism or the side length of a cube can involve square roots.
Understanding \(2\sqrt{7}\) in geometric contexts helps in solving various problems involving lengths, areas, and volumes, illustrating the interplay between algebra and geometry.
2 Square Root of 7 in Algebra
The expression \(2\sqrt{7}\) is frequently encountered in algebraic contexts. Understanding how to work with this expression can simplify solving equations and manipulating algebraic expressions. Here's a detailed look at its applications in algebra:
-
Simplifying Expressions:
Algebraic expressions often involve square roots. For example, consider the expression:
\[
3(2\sqrt{7}) + 5\sqrt{7}
\]This can be simplified by combining like terms:
\[
3 \times 2\sqrt{7} + 5\sqrt{7} = 6\sqrt{7} + 5\sqrt{7} = 11\sqrt{7}
\] -
Solving Equations:
Expressions involving \(2\sqrt{7}\) can appear in algebraic equations. For instance:
\[
x + 2\sqrt{7} = 10
\]To solve for \(x\), isolate the variable:
\[
x = 10 - 2\sqrt{7}
\] -
Quadratic Equations:
Square roots are common in the solutions to quadratic equations. For example, consider the quadratic equation:
\[
x^2 - 2x - 14 = 0
\]Using the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\), where \(a = 1\), \(b = -2\), and \(c = -14\), we get:
\[
x = \frac{2 \pm \sqrt{4 + 56}}{2} = \frac{2 \pm \sqrt{60}}{2} = \frac{2 \pm 2\sqrt{15}}{2} = 1 \pm \sqrt{15}
\] -
Rationalizing Denominators:
When square roots appear in denominators, it is often useful to rationalize them. For instance:
\[
\frac{1}{2\sqrt{7}} = \frac{1}{2\sqrt{7}} \times \frac{\sqrt{7}}{\sqrt{7}} = \frac{\sqrt{7}}{14}
\] -
Inequalities:
Expressions involving \(2\sqrt{7}\) can also appear in inequalities. For example:
\[
x > 2\sqrt{7}
\]This inequality indicates that \(x\) must be greater than approximately 5.2915.
By understanding how to manipulate and solve equations involving \(2\sqrt{7}\), one can effectively tackle a wide range of algebraic problems, illustrating the versatility and importance of this expression in algebra.
2 Square Root of 7 in Trigonometry
The number \( 2\sqrt{7} \) appears in trigonometric contexts, particularly when calculating angles or lengths involving triangles or circles. One notable application is in the calculation of angles and sides in trigonometric functions such as sine, cosine, and tangent.
In trigonometry, \( 2\sqrt{7} \) can be involved in calculating specific angles or triangle dimensions using the sine, cosine, and tangent functions. For instance, it might appear in angle calculations where the sides of a triangle are known, and the trigonometric ratios need to be determined.
Moreover, \( 2\sqrt{7} \) plays a role in understanding the relationships between angles and sides of triangles, especially in contexts where exact values are required rather than approximations.
Visualizing 2 Square Root of 7
Visualizing the value of \(2 \sqrt{7}\) can be made simpler by breaking down its components and using geometric representations. Here, we'll explore step-by-step methods to visualize this expression both numerically and geometrically.
Numerical Visualization
First, let's calculate the numerical value of \(2 \sqrt{7}\). The square root of 7 is approximately 2.6457513110645906. Therefore:
\[
2 \sqrt{7} = 2 \times 2.6457513110645906 \approx 5.291502622129181
\]
Geometric Visualization
We can visualize \(2 \sqrt{7}\) using geometric shapes such as rectangles and right triangles.
- Square Root on a Number Line:
- Draw a number line and mark the point representing \(\sqrt{7}\) at approximately 2.645.
- To represent \(2 \sqrt{7}\), double this distance on the number line, placing the mark at approximately 5.291.
- Right Triangle Representation:
- Construct a right triangle where one leg is \(\sqrt{7}\) units long.
- If the hypotenuse is twice the length of this leg, then the length of the hypotenuse will be \(2 \sqrt{7}\).
For example, if the legs of the triangle are \(\sqrt{7}\) and 1 unit respectively, the hypotenuse \(h\) can be calculated using the Pythagorean theorem:
\[
h = \sqrt{(\sqrt{7})^2 + 1^2} = \sqrt{7 + 1} = \sqrt{8} = 2 \sqrt{2}
\]To get \(2 \sqrt{7}\) directly, the leg adjacent to the right angle can be designed to meet the desired ratio.
- Rectangle Visualization:
- Draw a rectangle with one side length equal to \(2\) and the other side equal to \(\sqrt{7}\).
- The diagonal of this rectangle will visually represent \(2 \sqrt{7}\).
- Using the Pythagorean theorem again, the diagonal \(d\) is:
\[
d = \sqrt{(2)^2 + (\sqrt{7})^2} = \sqrt{4 + 7} = \sqrt{11}
\]
Graphical Representation
Consider plotting \(2 \sqrt{7}\) on a graph. Here’s a simple table to help visualize the value in different contexts:
| Expression | Approximate Value |
|---|---|
| \(\sqrt{7}\) | 2.6457513110645906 |
| \(2 \sqrt{7}\) | 5.291502622129181 |
By using these methods, one can gain a better understanding and visualization of the value \(2 \sqrt{7}\) in both numerical and geometric forms.
Historical Context of Square Roots
The concept of square roots has a rich and fascinating history, dating back to ancient civilizations. Here's a comprehensive look at how the understanding and use of square roots evolved over time:
- Ancient Babylonian Mathematics:
The Babylonians, around 1800 BCE, used a method similar to the one we use today to approximate square roots. They employed a form of iterative algorithm to find square roots, recorded on clay tablets.
- Greek Contributions:
The Greeks made significant advancements in mathematics. The mathematician Pythagoras (c. 570 – c. 495 BCE) and his followers were among the first to study square roots, particularly in relation to geometric shapes. They discovered that the diagonal of a square with side length 1 is the square root of 2, marking one of the earliest known uses of irrational numbers.
- Indian Mathematicians:
In ancient India, mathematicians such as Aryabhata (476–550 CE) developed methods for finding square roots. Aryabhata's work in "Aryabhatiya" includes techniques for extracting square roots that were quite advanced for their time.
- Islamic Golden Age:
During the Islamic Golden Age (8th to 14th century), scholars like Al-Khwarizmi made significant contributions to algebra and arithmetic, including methods for calculating square roots. His work laid the foundation for modern algebra.
- European Renaissance:
In the 16th century, European mathematicians such as Gerolamo Cardano and Rafael Bombelli expanded on previous works and further developed the understanding of square roots, including those of negative numbers, leading to the concept of complex numbers.
The journey of the square root from ancient algorithms to modern mathematical concepts demonstrates the evolution of mathematical thought and its impact on various fields of science and engineering. Today, the square root is a fundamental concept in mathematics, essential in various applications from geometry to complex analysis.
Advanced Mathematical Proofs Involving 2 Square Root of 7
In this section, we delve into advanced mathematical proofs involving \(2\sqrt{7}\). These proofs illustrate the depth and rigor of mathematical concepts applied to this particular value.
Proof of Irrationality of \(\sqrt{7}\)
To understand the properties of \(2\sqrt{7}\), we first explore the irrationality of \(\sqrt{7}\). Assume, for contradiction, that \(\sqrt{7}\) is rational, and can be expressed as a fraction in its lowest terms:
\[
\sqrt{7} = \frac{a}{b}
\]
Squaring both sides, we get:
\[
7 = \frac{a^2}{b^2} \implies 7b^2 = a^2
\]
This implies that \(a^2\) is a multiple of 7, hence \(a\) must be a multiple of 7. Let \(a = 7k\) for some integer \(k\). Substituting back, we get:
\[
7b^2 = (7k)^2 \implies 7b^2 = 49k^2 \implies b^2 = 7k^2
\]
This means \(b^2\) is also a multiple of 7, hence \(b\) must be a multiple of 7. Therefore, \(a\) and \(b\) have a common factor of 7, contradicting the assumption that \(\frac{a}{b}\) is in its lowest terms. Thus, \(\sqrt{7}\) is irrational.
Proof Involving \(2\sqrt{7}\)
Given that \(\sqrt{7}\) is irrational, \(2\sqrt{7}\) is also irrational. We can extend the proof by contradiction to show this:
\[
2\sqrt{7} = \frac{p}{q}
\]
Squaring both sides, we get:
\[
4 \cdot 7 = \frac{p^2}{q^2} \implies 28q^2 = p^2
\]
This implies \(p^2\) is a multiple of 28, and hence \(p\) must be a multiple of \(\sqrt{28}\), which is not an integer. Thus, \(2\sqrt{7}\) cannot be rational.
Geometric Interpretation and Proof
Another approach involves geometric interpretation. Consider a right triangle where one leg is \(1\) and the hypotenuse is \(\sqrt{7}\). If \(\sqrt{7}\) were rational, we could find a similar triangle with integer sides by scaling up. However, this leads to an infinite regress of smaller and smaller triangles, each with a hypotenuse of \(\sqrt{7}\), proving it cannot be rational.
Algebraic Proof Using Contradiction
For any integers \(a\) and \(b\), assume \(2\sqrt{7} = \frac{a}{b}\):
\[
(2\sqrt{7})^2 = \left(\frac{a}{b}\right)^2 \implies 4 \cdot 7 = \frac{a^2}{b^2} \implies 28b^2 = a^2
\]
This implies that \(a^2\) must be a multiple of 28, and hence \(a\) must be a multiple of \(\sqrt{28}\), an impossibility as discussed. Therefore, \(2\sqrt{7}\) is irrational.
These proofs underline the inherent complexity and beauty of mathematical principles applied to specific values like \(2\sqrt{7}\).
Common Misconceptions About Square Roots
Square roots, despite their fundamental role in mathematics, are often misunderstood. Here are some common misconceptions and clarifications:
- Square roots always yield positive results: A common misconception is that square roots only yield positive results. In reality, every positive number has two square roots: one positive and one negative. For example, both \( \sqrt{25} = 5 \) and \( \sqrt{25} = -5 \).
- Square roots of negative numbers are undefined: While it's true that there are no real square roots of negative numbers, they do have imaginary square roots. For example, \( \sqrt{-1} \) is defined as \( i \), the imaginary unit.
- Square roots of non-perfect squares are irrational: Another misconception is that the square root of any non-perfect square is always irrational. While this is generally true, it's important to note the difference between rational and irrational numbers, where rational numbers can be expressed as a fraction, and irrational numbers cannot.
- Square roots are always less than the original number: This is not always the case. For numbers between 0 and 1, the square root is actually greater than the original number. For instance, \( \sqrt{0.25} = 0.5 \), which is greater than 0.25.
Understanding these nuances helps to build a clearer and more accurate foundation in mathematics. By addressing these misconceptions, learners can better appreciate the properties and applications of square roots.
Real-World Examples of 2 Square Root of 7
The value of \(2 \sqrt{7}\) approximately equals 5.291502622. This value finds applications in various fields such as geometry, physics, and engineering. Here are some real-world examples:
- Geometry: In geometry, the value of \(2 \sqrt{7}\) can be used to determine the diagonal of a rectangle. For instance, if one side of the rectangle is \(2 \sqrt{7}\) units long and the other side is 3 units long, the diagonal can be calculated using the Pythagorean theorem:
- Physics: In physics, the value of \(2 \sqrt{7}\) might be used in calculating velocities or forces. For example, in a situation where an object travels along two perpendicular vectors of magnitudes \(2 \sqrt{7}\) and 4 units respectively, the resultant vector would be:
- Engineering: Engineers might use the value \(2 \sqrt{7}\) when dealing with stress and strain calculations in materials. For instance, if the displacement in a structure is \(2 \sqrt{7}\) meters under a specific load, this value helps in calculating the stress experienced by the structure.
- Statistics: In statistics, the concept of the square root is frequently used to calculate the standard deviation. For example, if you have a variance of 7, the standard deviation would be \( \sqrt{7} \). In cases where scaling is involved, \(2 \sqrt{7}\) might appear as part of the calculation for aggregated data sets.
- Computer Graphics: In computer graphics, calculations involving distances between points in space often use square roots. For instance, in 3D space, the distance between two points could involve a computation like:
\[
d = \sqrt{(2 \sqrt{7})^2 + 3^2} = \sqrt{4 \times 7 + 9} = \sqrt{28 + 9} = \sqrt{37} \approx 6.08
\]
\[
\text{Resultant} = \sqrt{(2 \sqrt{7})^2 + 4^2} = \sqrt{28 + 16} = \sqrt{44} \approx 6.63 \text{ units}
\]
\[
\text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\]
where one of the coordinates involves \(2 \sqrt{7}\).
These examples illustrate how the value \(2 \sqrt{7}\) can be applied in various practical scenarios, demonstrating its significance beyond just a mathematical curiosity.
Further Reading and Resources
For those interested in delving deeper into the topic of the square root of 7, here are some excellent resources and further readings:
-
Books on Algebra and Number Theory
- Algebra and Trigonometry by Michael Sullivan - This book provides comprehensive coverage of algebraic concepts, including detailed explanations of square roots and their properties.
- Elementary Number Theory by David M. Burton - A great resource for understanding the fundamental concepts of number theory, including roots and their applications.
-
Online Calculators and Tools
- - A versatile online calculator that can help with calculating the square root of 7 and other algebraic operations.
- - This website offers a detailed explanation of square roots and a calculator specifically for finding the square root of 7.
-
Academic Journals and Papers
- - A digital library for academic journals, books, and primary sources. Search for papers on square roots and their applications in various fields.
- - Access to a large database of scientific and mathematical research papers, including those focusing on the properties and uses of square roots.
-
Educational Videos and Tutorials
- - Offers free tutorials and videos explaining the concept of square roots and their applications in mathematics.
- - Search for educational channels such as Numberphile or Mathologer, which provide in-depth videos on mathematical topics including the square root of 7.
These resources should provide a thorough understanding and additional insights into the concept of square roots, particularly the square root of 7. Happy learning!
Tìm hiểu về căn bậc hai cùng thầy J trong video này. Hiểu rõ khái niệm và cách áp dụng căn bậc hai vào các bài toán thực tế.
Căn bậc hai là gì? | Toán học với thầy J
READ MORE:
2 căn bậc hai của 7, rút gọn thành một căn, rút gọn thành một biểu thức