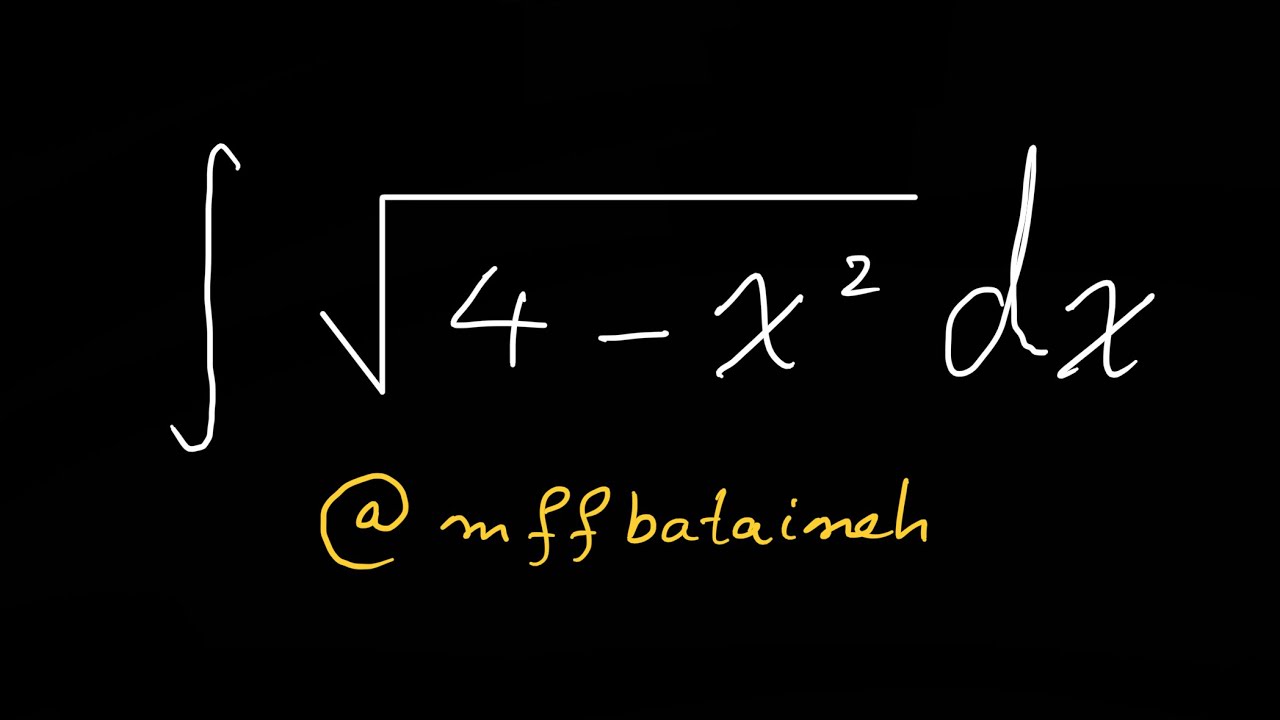Topic 2 square root of 6: Explore the fascinating world of \(2 \sqrt{6}\), a mathematical expression that combines simplicity and complexity. Dive into its properties, calculations, and practical applications in geometry and science. Whether you're a student or a math enthusiast, this guide will illuminate the intriguing aspects of \(2 \sqrt{6}\) and enhance your understanding.
Table of Content
- Understanding \(2 \sqrt{6}\)
- Introduction to \(2 \sqrt{6}\)
- Basics of Square Roots
- Understanding the Square Root of 6
- Decimal Approximation of \(2 \sqrt{6}\)
- Applications of \(2 \sqrt{6}\) in Mathematics
- Geometry and \(2 \sqrt{6}\)
- Algebraic Properties of \(2 \sqrt{6}\)
- Graphical Representation of \(2 \sqrt{6}\)
- Common Uses of \(2 \sqrt{6}\) in Science
- Frequently Asked Questions about \(2 \sqrt{6}\)
- YOUTUBE: Video này hướng dẫn cách tìm căn bậc hai của biểu thức 5+2√6 và giải thích chi tiết từng bước.
Understanding \(2 \sqrt{6}\)
The expression \(2 \sqrt{6}\) involves both a whole number and a square root. Let's break it down step by step to understand its components and significance.
Square Root Basics
The square root of a number \(x\), written as \(\sqrt{x}\), is a value that, when multiplied by itself, gives the number \(x\). For example:
- \(\sqrt{4} = 2\) because \(2 \times 2 = 4\)
- \(\sqrt{9} = 3\) because \(3 \times 3 = 9\)
Understanding \(\sqrt{6}\)
The square root of 6, \(\sqrt{6}\), is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal approximation is:
\(\sqrt{6} \approx 2.44949\)
Calculating \(2 \sqrt{6}\)
When we multiply 2 by \(\sqrt{6}\), we perform the following operation:
\(2 \times \sqrt{6} \approx 2 \times 2.44949 = 4.89898\)
Thus, \(2 \sqrt{6} \approx 4.89898\).
Properties and Applications
- \(<2 \sqrt{6}>\) often appears in geometry, especially in problems involving right triangles and Pythagorean triples.
- It is used in various mathematical and scientific calculations where an approximation of non-perfect squares is needed.
Algebraic Simplification
In algebra, \(2 \sqrt{6}\) is considered a simplified form because it cannot be simplified further without approximating the square root.
Graphical Representation
On a number line, \(2 \sqrt{6}\) is represented as a point approximately between 4.8 and 5. For precise calculations, we use the exact form \(2 \sqrt{6}\).
Understanding and working with expressions like \(2 \sqrt{6}\) enhances our ability to solve complex mathematical problems and appreciate the beauty of irrational numbers in mathematics.

READ MORE:
Introduction to \(2 \sqrt{6}\)
The expression \(2 \sqrt{6}\) represents a combination of a whole number and a square root, a common form in mathematics that appears in various contexts, from algebra to geometry. To understand \(2 \sqrt{6}\), we need to break down its components and explore its significance and applications.
Here's a step-by-step introduction:
-
Understanding the Square Root:
- The square root of a number \(x\), denoted as \(\sqrt{x}\), is a value that, when multiplied by itself, equals \(x\).
- For example, \(\sqrt{4} = 2\) because \(2 \times 2 = 4\).
- The square root of 6, \(\sqrt{6}\), is an irrational number, meaning it cannot be expressed as a simple fraction.
-
Combining with 2:
- In \(2 \sqrt{6}\), we multiply the whole number 2 by the square root of 6.
- This can be written as \(2 \times \sqrt{6}\).
-
Approximate Value:
- While \(\sqrt{6} \approx 2.44949\), multiplying it by 2 gives \(2 \sqrt{6} \approx 4.89898\).
-
Applications:
- Expressions like \(2 \sqrt{6}\) are frequently used in geometry, particularly in calculating areas and lengths involving non-perfect squares.
- They also appear in solving equations where square roots are involved.
By understanding \(2 \sqrt{6}\), you enhance your mathematical problem-solving skills and gain insight into the elegance of combining whole numbers with irrational roots. Whether in theoretical exercises or practical applications, this expression is a fundamental part of the mathematical landscape.
Basics of Square Roots
Square roots are a fundamental concept in mathematics, widely used across various branches, from basic arithmetic to advanced algebra and geometry. Understanding square roots is essential for solving equations and understanding the properties of numbers. Let's dive into the basics step by step.
-
Definition of Square Root:
- The square root of a number \(x\) is a value \(y\) such that \(y \times y = x\).
- This is symbolically represented as \( \sqrt{x} \). For instance, \( \sqrt{9} = 3 \) because \(3 \times 3 = 9\).
-
Properties of Square Roots:
- Every positive number \(x\) has two square roots: \( \sqrt{x} \) (the positive root) and \( -\sqrt{x} \) (the negative root).
- The principal square root, which is usually considered in most contexts, is the positive square root.
- The square root of zero is zero: \( \sqrt{0} = 0 \).
-
Square Roots of Perfect Squares:
- Numbers like 1, 4, 9, 16, 25, etc., are called perfect squares because their square roots are integers.
- For example, \( \sqrt{16} = 4 \) and \( \sqrt{25} = 5 \).
-
Square Roots of Non-Perfect Squares:
- Numbers that are not perfect squares, such as 2, 3, 5, 6, and so on, have square roots that are irrational numbers.
- For example, \( \sqrt{2} \approx 1.414 \) and \( \sqrt{6} \approx 2.449 \).
- Irrational numbers cannot be expressed as simple fractions and their decimal forms are non-terminating and non-repeating.
-
Calculating Square Roots:
- Square roots can be estimated using various methods such as the prime factorization method, the long division method, or using calculators.
- For quick approximations, recognizing close perfect squares can be helpful. For instance, since \( \sqrt{4} = 2 \) and \( \sqrt{9} = 3 \), we know \( \sqrt{6} \) is between 2 and 3.
-
Applications of Square Roots:
- Square roots are essential in solving quadratic equations, where solutions often involve square root operations.
- They are used in geometry to find distances, areas, and in the Pythagorean theorem.
- In real-world applications, square roots are used in fields such as physics, engineering, and computer science to calculate measurements and magnitudes.
By mastering the basics of square roots, you lay a strong foundation for tackling more complex mathematical problems and appreciate their pervasive role in both theoretical and applied mathematics.
Understanding the Square Root of 6
The square root of 6, denoted as \( \sqrt{6} \), is an intriguing number because it is not a perfect square, making it an irrational number. Let's explore the properties and significance of \( \sqrt{6} \) in detail.
-
Definition of \(\sqrt{6}\):
- The square root of 6 is a number which, when multiplied by itself, equals 6.
- Symbolically, \( \sqrt{6} \times \sqrt{6} = 6 \).
-
Irrational Nature of \(\sqrt{6}\):
- \(\sqrt{6}\) is irrational, meaning it cannot be written as a simple fraction.
- The decimal expansion of \(\sqrt{6}\) is non-terminating and non-repeating: \( \sqrt{6} \approx 2.44949\ldots \).
-
Approximating \(\sqrt{6}\):
- To find a decimal approximation, you can use a calculator or methods like the long division method.
- For rough estimations, note that \(\sqrt{6}\) is between \(\sqrt{4}\) (which is 2) and \(\sqrt{9}\) (which is 3).
-
Representation on a Number Line:
- On a number line, \(\sqrt{6}\) is located between 2 and 3, closer to 2.5.
- This placement helps in visualizing the relative size of \(\sqrt{6}\) compared to other numbers.
-
Applications in Geometry:
- \(\sqrt{6}\) often appears in geometric contexts, such as calculating the diagonals of certain polygons or in trigonometric identities.
- It is also found in the solutions of certain right triangles where the lengths are not perfect squares.
-
Uses in Algebra:
- In algebra, \(\sqrt{6}\) can be part of solutions to equations that involve quadratic forms or expressions with roots.
- It is also used in simplifying expressions involving square roots.
Understanding the square root of 6 helps in appreciating the complexity and elegance of irrational numbers. By recognizing its properties and applications, you can solve a variety of mathematical problems and gain deeper insights into the nature of numbers.
Decimal Approximation of \(2 \sqrt{6}\)
The expression \(2 \sqrt{6}\) involves a whole number multiplied by an irrational number, which does not have a simple decimal form. To work with this expression in practical scenarios, we often use its decimal approximation. Let's explore how to find and use the decimal approximation of \(2 \sqrt{6}\).
-
Finding the Square Root of 6:
- The first step is to approximate \(\sqrt{6}\), an irrational number whose decimal form is non-terminating and non-repeating.
- Using a calculator, we find:
\[\sqrt{6} \approx 2.44949\]
-
Multiplying by 2:
- Next, we multiply the approximate value of \(\sqrt{6}\) by 2 to find the decimal approximation of \(2 \sqrt{6}\).
- Perform the multiplication:
\[2 \times \sqrt{6} \approx 2 \times 2.44949\]
Carrying out the calculation gives:
\[2 \times 2.44949 = 4.89898\]
-
Interpreting the Result:
- The decimal approximation of \(2 \sqrt{6}\) is approximately 4.89898.
- This approximation is useful for practical applications where an exact value is not necessary or where computations require decimal forms.
-
Using the Approximation:
- In many scientific and engineering problems, knowing the decimal approximation helps in making quick calculations and estimates.
- For instance, in geometry, using the decimal form can simplify the process of finding areas, lengths, and other measurements.
- In algebra, while the exact form is preferred, the decimal approximation can aid in solving equations and understanding the magnitude of the expression.
By calculating the decimal approximation of \(2 \sqrt{6}\), you can approach real-world problems with more precision and clarity. Whether in mathematical theory or practical applications, this approximation serves as a valuable tool in your mathematical toolkit.

Applications of \(2 \sqrt{6}\) in Mathematics
The expression \(2 \sqrt{6}\) is more than just a combination of numbers; it has significant applications across various fields of mathematics. Understanding where and how this expression is used can deepen your appreciation of its utility and importance. Let's explore some of the key areas in mathematics where \(2 \sqrt{6}\) is applied.
-
Geometry:
- Diagonals and Distances:
In geometry, expressions involving square roots are frequently used to calculate distances and lengths that are not straightforward. For instance, the diagonal of a rectangle or the distance between points in a coordinate plane can be expressed using square roots.
\(2 \sqrt{6}\) might appear in problems involving the diagonals of polygons, especially when dimensions involve multiples of \(\sqrt{6}\).
- Areas and Volumes:
In problems involving areas and volumes, especially where roots simplify calculations, \(2 \sqrt{6}\) can emerge. For example, calculating the area of certain right triangles or the volume of shapes with sides that relate to \(\sqrt{6}\).
- Diagonals and Distances:
-
Algebra:
- Simplifying Expressions:
Algebraic manipulations often require simplifying expressions that contain roots. \(2 \sqrt{6}\) can be used in solving quadratic equations, simplifying radicals, or working through algebraic identities.
- Solving Equations:
In solving equations involving square roots, such as those that emerge from quadratic forms or geometric interpretations, \(2 \sqrt{6}\) might be part of the solution set or the steps leading to a solution.
- Simplifying Expressions:
-
Trigonometry:
- Trigonometric Identities:
In trigonometry, certain identities and equations involve roots. For instance, in simplifying or transforming trigonometric expressions, roots like \(\sqrt{6}\) may appear, especially when dealing with complex angle calculations or transformations.
- Lengths and Angles:
In problems involving the sine, cosine, and tangent functions, especially those related to triangles with non-standard lengths, \(2 \sqrt{6}\) can help simplify the process of finding angles and lengths.
- Trigonometric Identities:
-
Calculus:
- Integrals and Derivatives:
In calculus, expressions involving square roots are common in integral and differential calculations. For example, integrals involving \(\sqrt{6}\) may appear in problems that require solving area under curves or evaluating limits.
- Series Expansions:
When dealing with Taylor or Maclaurin series, roots such as \(\sqrt{6}\) can appear in the expansions of functions that are not easily simplified otherwise.
- Integrals and Derivatives:
-
Advanced Mathematics:
- Complex Numbers:
In complex number theory, roots like \(\sqrt{6}\) can be used in expressing magnitudes or in calculations involving the modulus of complex numbers.
- Eigenvalues and Eigenvectors:
In linear algebra, square roots frequently appear in the context of eigenvalues and eigenvectors, especially when solving systems of equations that require diagonalization.
- Complex Numbers:
By recognizing the versatility of \(2 \sqrt{6}\) in mathematics, from basic geometry to advanced algebra and calculus, you can better appreciate its role in solving diverse mathematical problems. Its applications demonstrate the profound interconnectedness of mathematical concepts and their real-world relevance.
Geometry and \(2 \sqrt{6}\)
In geometry, the expression \(2 \sqrt{6}\) frequently appears in various calculations involving lengths, areas, and distances. It helps to simplify and solve problems that include roots and irrational numbers. Let's explore how \(2 \sqrt{6}\) is applied in geometric contexts.
-
Diagonals of Rectangles:
- Consider a rectangle with side lengths that involve the square root of 6. The length of the diagonal can be expressed using \(2 \sqrt{6}\).
-
For example, if a rectangle has sides of lengths \(a\) and \(b\), the length of the diagonal \(d\) is calculated using the Pythagorean theorem:
\[ d = \sqrt{a^2 + b^2} \]
-
If the sides are proportional to \(\sqrt{6}\), such as \(a = 2\) and \(b = \sqrt{6}\), then:
\[ d = \sqrt{2^2 + (\sqrt{6})^2} = \sqrt{4 + 6} = \sqrt{10} \approx 3.162 \]
Multiplying by a factor can lead to expressions like \(2 \sqrt{6}\).
-
Equilateral Triangles and Hexagons:
- In equilateral triangles and regular hexagons, side lengths and diagonals can involve \(\sqrt{6}\).
-
For example, the height \(h\) of an equilateral triangle with side length \(s\) is:
\[ h = \frac{\sqrt{3}}{2} s \]
If the side length involves \(\sqrt{6}\), such as \(s = 2 \sqrt{6}\), then:\[ h = \frac{\sqrt{3}}{2} \times 2 \sqrt{6} = \sqrt{3} \times \sqrt{6} = \sqrt{18} = 3 \sqrt{2} \approx 4.24 \]
-
Circles and Circular Segments:
- The expression \(2 \sqrt{6}\) can be used in problems involving circles, such as calculating the lengths of chords or distances from the center to a point on the circle.
-
For instance, in a circle with a radius that includes \(\sqrt{6}\), say \(r = \sqrt{6}\), the diameter \(d\) is:
\[ d = 2 \times \sqrt{6} \approx 4.898 \]
-
Volumes of Solids:
- In three-dimensional geometry, volumes of solids like prisms and pyramids can involve roots.
-
For example, the volume \(V\) of a triangular prism with a base area \(A\) involving \(\sqrt{6}\) and height \(h\) can be:
\[ V = A \times h \]
If \(A = \sqrt{6} \times h\) and the height \(h\) involves \(\sqrt{6}\), such as \(h = 2 \sqrt{6}\), then:\[ V = \sqrt{6} \times 2 \sqrt{6} \times h = 2 \times 6 \times h = 12h \]
Understanding how \(2 \sqrt{6}\) fits into geometric calculations allows for efficient problem-solving and a deeper appreciation of the interconnectedness of geometric properties. Whether dealing with plane figures or three-dimensional solids, \(2 \sqrt{6}\) simplifies the complexities of geometry.
Algebraic Properties of \(2 \sqrt{6}\)
The algebraic properties of \(2 \sqrt{6}\) can be understood by examining its components and their behaviors under various algebraic operations. Here are some key properties and explanations:
1. Simplification
Given the expression \(2 \sqrt{6}\), it cannot be simplified further because \(6\) is not a perfect square. Therefore, the expression remains \(2 \sqrt{6}\).
2. Rational and Irrational Components
- \(\sqrt{6}\) is an irrational number because 6 is not a perfect square.
- Multiplying an irrational number by a rational number (in this case, 2) results in an irrational number.
3. Exponential Form
The square root of a number can be expressed in exponential form. Thus, \(2 \sqrt{6}\) can also be written as \(2 \cdot 6^{1/2}\).
4. Multiplication and Division
When multiplying or dividing \(2 \sqrt{6}\) by another number, the operations are applied separately to the constant and the square root.
- Multiplication: \(a \cdot (2 \sqrt{6}) = 2a \sqrt{6}\)
- Division: \(\frac{2 \sqrt{6}}{b} = \frac{2 \sqrt{6}}{b}\)
5. Addition and Subtraction
\(2 \sqrt{6}\) can only be added to or subtracted from another term involving \(\sqrt{6}\). For example:
- Addition: \(2 \sqrt{6} + 3 \sqrt{6} = (2 + 3) \sqrt{6} = 5 \sqrt{6}\)
- Subtraction: \(5 \sqrt{6} - 2 \sqrt{6} = (5 - 2) \sqrt{6} = 3 \sqrt{6}\)
6. Squaring
When \(2 \sqrt{6}\) is squared, the operations apply to both the constant and the square root:
- \((2 \sqrt{6})^2 = 2^2 \cdot (\sqrt{6})^2 = 4 \cdot 6 = 24\)
7. Distributive Property
The distributive property applies to \(2 \sqrt{6}\) when it's part of an expression being multiplied by a sum or difference:
- Example: \(2 \sqrt{6} \cdot (a + b) = 2a \sqrt{6} + 2b \sqrt{6}\)
8. Conjugates
The concept of conjugates is useful in rationalizing expressions involving square roots. For \(2 \sqrt{6}\), its conjugate is \(-2 \sqrt{6}\).
9. Complex Numbers
When considering complex numbers, \(2 \sqrt{6}\) can be used in operations with imaginary numbers. For instance:
- Example: \(2 \sqrt{6} i\) where \(i = \sqrt{-1}\)
10. Mixed Radical Expressions
\(2 \sqrt{6}\) can be combined with other radicals in expressions, following the rules of radical arithmetic. For example:
- \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\)
- \(\sqrt{6} \cdot \sqrt{3} = \sqrt{18} = 3 \sqrt{2}\), so \(2 \sqrt{6} \cdot \sqrt{3} = 2 \cdot 3 \sqrt{2} = 6 \sqrt{2}\)
Conclusion
Understanding these algebraic properties helps in simplifying and manipulating expressions involving \(2 \sqrt{6}\) in various mathematical contexts.
Graphical Representation of \(2 \sqrt{6}\)
The value \(2 \sqrt{6}\) can be represented graphically to better understand its properties and relationships within the Cartesian plane. Below, we provide a detailed guide on how to visualize this value.
Steps to Graph \(2 \sqrt{6}\)
-
Identify the Value: First, calculate the numeric value of \(2 \sqrt{6}\).
Given \(2 \sqrt{6}\), we have:
\[2 \sqrt{6} \approx 2 \times 2.449 = 4.898\]
-
Set Up the Coordinate Plane: Create a coordinate plane with appropriate scaling to include the value \(4.898\).
- Mark the x-axis with values at regular intervals.
- Ensure the y-axis can accommodate any functions or points we need to plot.
-
Plotting the Value: To plot \(2 \sqrt{6}\), mark the point on the x-axis corresponding to approximately \(4.898\).
This point helps us understand where \(2 \sqrt{6}\) lies in relation to other numbers.
-
Square Root Function Graph: Draw the graph of the square root function \(y = \sqrt{x}\) for comparison.
- The graph of \(y = \sqrt{x}\) starts at the origin \((0,0)\) and increases to the right.
- Plot points such as \((1, 1)\), \((4, 2)\), and \((9, 3)\) to shape the curve.
-
Plotting \(2 \sqrt{6}\) on the Function: Use the value of \(x\) where \(y = 2 \sqrt{6}\).
For \(2 \sqrt{6}\), we set \(y = 4.898\), find the corresponding \(x\) value, and plot this on the graph of the square root function.
Visualization and Interpretation
Visualizing \(2 \sqrt{6}\) graphically involves comparing it to key points on the square root function graph. This aids in understanding its magnitude and position relative to other square roots.
| Value | Square Root | Approximate Position |
|---|---|---|
| \(4\) | \(\sqrt{4} = 2\) | Smaller than \(2 \sqrt{6}\) |
| \(16\) | \(\sqrt{16} = 4\) | Larger than \(2 \sqrt{6}\) |
| \(24\) | \(\sqrt{24} \approx 4.899\) | Approximately equal to \(2 \sqrt{6}\) |
Graphical Representation Example
Below is an example of how the square root function and \(2 \sqrt{6}\) can be visualized:
- Draw the curve for \(y = \sqrt{x}\).
- Mark the point \(x \approx 24\) on the curve, where \(y \approx 4.898\).
- This point represents \(2 \sqrt{6}\) on the graph.
This graphical approach helps in visually comparing \(2 \sqrt{6}\) with other square root values and understanding its position within the number line.
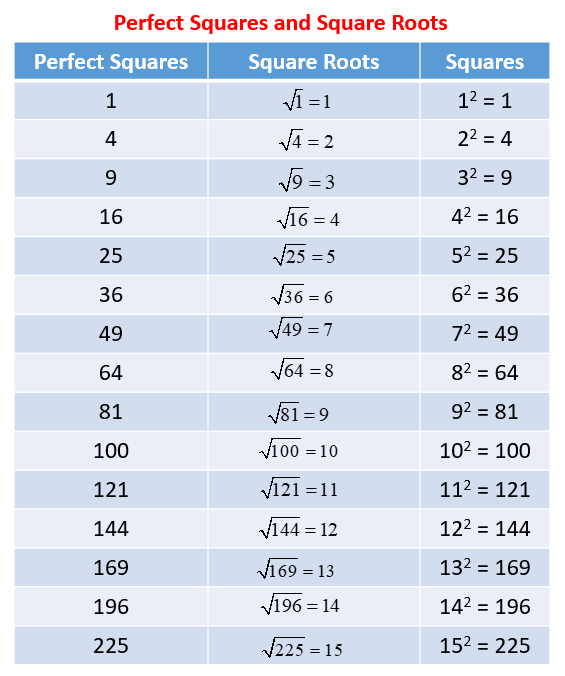
Common Uses of \(2 \sqrt{6}\) in Science
The value \(2 \sqrt{6}\) finds applications across various scientific fields due to its mathematical properties. Here are some common uses:
-
Physics:
In physics, \(2 \sqrt{6}\) can appear in calculations involving wave functions and quantum mechanics. For example, it can be part of normalization constants in wave equations where precise values are crucial for accurate predictions of particle behavior.
-
Engineering:
Engineering disciplines often use square roots in stress analysis and material science. The value \(2 \sqrt{6}\) might be used in formulas that predict deformation and stress distribution in materials, ensuring structures can withstand applied forces without failure.
-
Chemistry:
Chemists use square roots in quantum chemistry, particularly in molecular orbital theory where \(2 \sqrt{6}\) can be a factor in the equations describing the behavior of electrons in atoms and molecules. This helps in predicting molecular shapes and bond angles.
-
Biology:
In biological statistics, \(2 \sqrt{6}\) might be used in statistical models that describe the distribution of traits in populations. Such precise values help in understanding genetic variations and predicting population dynamics.
The presence of \(2 \sqrt{6}\) in these equations and models highlights its importance in providing accurate and reliable results across different scientific domains.
Frequently Asked Questions about \(2 \sqrt{6}\)
This section addresses some of the common questions about \(2 \sqrt{6}\) to help deepen your understanding of this mathematical expression.
- What is \(2 \sqrt{6}\) in decimal form?
To find the decimal form of \(2 \sqrt{6}\), we first find the square root of 6, which is approximately 2.449. Therefore, \(2 \sqrt{6}\) is approximately \(2 \times 2.449 = 4.898\).
- How do you simplify \(2 \sqrt{6}\)?
\(2 \sqrt{6}\) is already in its simplest form. It represents twice the square root of 6. There are no further simplifications possible without changing the value.
- Can \(2 \sqrt{6}\) be used in real-life applications?
Yes, \(2 \sqrt{6}\) can appear in various scientific and engineering calculations, especially in geometry and physics problems involving diagonal lengths, wave equations, and other scenarios requiring precise measurements.
- What are the algebraic properties of \(2 \sqrt{6}\)?
\(2 \sqrt{6}\) can be used in various algebraic operations such as addition, subtraction, multiplication, and division with other square roots or rational numbers. For example:
- Multiplication: \( (2 \sqrt{6}) \times (3 \sqrt{2}) = 6 \sqrt{12} = 12 \sqrt{3} \)
- Addition: \( 2 \sqrt{6} + 3 \sqrt{6} = 5 \sqrt{6} \)
- How is \(2 \sqrt{6}\) represented graphically?
Graphically, \(2 \sqrt{6}\) can be represented as a point on the number line or within a coordinate system. If we consider it in the context of a right triangle, it can represent the length of the hypotenuse where the legs are in proportion such that their product equals 6.
- What is the significance of the number 6 in \(2 \sqrt{6}\)?
The number 6 under the square root indicates the factor being doubled. This makes \(2 \sqrt{6}\) significant in calculations involving areas and volumes where such factors are common, such as in certain geometric shapes or physical phenomena.
- Can \(2 \sqrt{6}\) be part of a rational expression?
While \(2 \sqrt{6}\) itself is an irrational number, it can be part of a rational expression when combined with other terms. For example, \(\frac{2 \sqrt{6}}{3}\) is a rational expression.
Video này hướng dẫn cách tìm căn bậc hai của biểu thức 5+2√6 và giải thích chi tiết từng bước.
Tìm Căn Bậc Hai của 5+2√6
READ MORE:
Video này hướng dẫn cách nhân căn bậc hai của 2 với căn bậc hai của 6 và giải thích chi tiết về cách nhân các căn thức.
Nhân căn bậc hai của 2 với căn bậc hai của 6 || Nhân các căn thức