Topic 2 square root 18: Discover how to simplify and understand the expression 2 √18 with our step-by-step guide. Learn the basics of square roots, prime factorization, and practical applications of simplified radicals. Perfect for students and math enthusiasts looking to enhance their skills and comprehension. Simplify your calculations and boost your confidence in mathematics today!
Table of Content
- Understanding the Expression: 2 √18
- Introduction to Simplifying Square Roots
- Understanding the Expression: 2 √18
- Step-by-Step Simplification Process
- Prime Factorization of 18
- Simplifying Square Roots Involving Perfect Squares
- Combining Simplified Factors
- Final Multiplication and Simplification
- Common Mistakes to Avoid
- Practical Applications of Simplified Radicals
- Frequently Asked Questions (FAQ)
- Conclusion and Summary
- YOUTUBE:
Understanding the Expression: 2 √18
The mathematical expression 2 \sqrt{18} can be simplified to make it easier to understand and work with. Let's break it down step-by-step.
Step-by-Step Simplification
Identify the square root component in the expression:
\sqrt{18}.Factorize the number inside the square root to find its prime factors:
18 = 2 \times 3^2.Rewrite the square root using its prime factors:
\sqrt{18} = \sqrt{2 \times 3^2}.Separate the factors inside the square root:
\sqrt{18} = \sqrt{2} \times \sqrt{3^2}.Simplify the square root of the perfect square:
\sqrt{3^2} = 3.Combine the simplified factors:
\sqrt{18} = 3 \sqrt{2}.Finally, multiply by the 2 outside the square root:
2 \sqrt{18} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}.
Simplified Result
Thus, the expression 2 \sqrt{18} simplifies to 6 \sqrt{2}.
Key Points to Remember
- Breaking down the number inside the square root into its prime factors helps in simplifying the expression.
- Recognizing and simplifying perfect squares within the square root is crucial.
- Multiplying the simplified square root by any outside coefficients is the final step.
Applications
Simplified radical expressions are useful in various fields of mathematics, including algebra, geometry, and calculus. They make complex calculations more manageable and help in solving equations more efficiently.

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots is a fundamental skill in mathematics that makes complex expressions more manageable. Understanding how to break down and simplify square roots can help in solving equations, performing calculations, and improving overall mathematical comprehension. Let's explore the basics and the step-by-step process of simplifying square roots using the example of 2 \sqrt{18}.
The process of simplifying square roots involves a few key steps:
- Identify the Number Inside the Square Root: Begin by examining the number under the square root sign. For example, in
\sqrt{18}, the number is 18. - Factorize the Number: Break down the number into its prime factors. Prime factorization of 18 gives us
18 = 2 \times 3^2. - Separate the Factors: Rewrite the square root expression using the prime factors. For example,
\sqrt{18} = \sqrt{2 \times 3^2}. - Simplify Perfect Squares: Identify and simplify any perfect square factors within the square root. In this case,
\sqrt{3^2} = 3. - Combine the Simplified Parts: Put the simplified parts back together. So,
\sqrt{18} = 3 \sqrt{2}. - Include Any Coefficients: If there is a coefficient outside the square root, multiply it by the simplified square root. For
2 \sqrt{18}, this results in2 \times 3 \sqrt{2} = 6 \sqrt{2}.
By following these steps, you can simplify any square root expression, making calculations more straightforward and easier to handle. Simplifying square roots is an essential skill that enhances problem-solving abilities in various mathematical contexts.
Understanding the Expression: 2 √18
The expression 2 \sqrt{18} might seem complex at first, but breaking it down step-by-step can make it much simpler to understand. This section will guide you through the process of simplifying this expression, helping you grasp the underlying concepts and techniques.
Let's start with the basic components of the expression:
- Square Root Component: The term
\sqrt{18}indicates the square root of 18. To simplify this, we need to factorize 18 into its prime factors. - Prime Factorization: The number 18 can be broken down into its prime factors:
18 = 2 \times 3 \times 3or18 = 2 \times 3^2. - Rewrite the Square Root: Using the prime factors, rewrite the square root expression:
\sqrt{18} = \sqrt{2 \times 3^2}. - Separate and Simplify: Separate the factors under the square root into simpler parts. Since 3 is squared, we can simplify this part of the expression:
\sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} = \sqrt{2} \times 3. - Simplify Further: Combine the simplified components:
\sqrt{18} = 3 \sqrt{2}. - Multiply by the Coefficient: Finally, include the coefficient outside the square root. In the expression
2 \sqrt{18}, multiply the simplified square root by 2:2 \sqrt{18} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}.
Therefore, the expression 2 \sqrt{18} simplifies to 6 \sqrt{2}. This process of simplification involves breaking down the number inside the square root into its prime factors, simplifying the square root of any perfect squares, and then combining these results with any coefficients outside the square root.
Understanding how to simplify expressions like 2 \sqrt{18} not only helps in mathematical calculations but also strengthens your problem-solving skills and enhances your ability to work with more complex mathematical expressions.
Step-by-Step Simplification Process
Simplifying the expression 2 \sqrt{18} involves breaking it down into manageable steps. This process will help you understand how to handle similar expressions and enhance your overall mathematical skills.
- Identify the Expression: Start with the given expression:
2 \sqrt{18}. - Prime Factorization: Break down the number inside the square root into its prime factors. For 18, the prime factorization is:
18 = 2 \times 3 \times 3or18 = 2 \times 3^2. - Rewrite the Square Root: Express the square root in terms of its prime factors:
\sqrt{18} = \sqrt{2 \times 3^2}. - Separate the Factors: Split the square root into separate square roots:
\sqrt{18} = \sqrt{2} \times \sqrt{3^2}. - Simplify the Square Root of the Perfect Square: Simplify the square root of the perfect square:
\sqrt{3^2} = 3. - Combine the Simplified Parts: Multiply the simplified parts together:
\sqrt{18} = 3 \sqrt{2}. - Include the Coefficient: Multiply the simplified square root by the coefficient outside the square root:
2 \sqrt{18} = 2 \times 3 \sqrt{2}. - Final Simplification: Complete the multiplication to get the simplified expression:
2 \times 3 \sqrt{2} = 6 \sqrt{2}.
Therefore, the expression 2 \sqrt{18} simplifies to 6 \sqrt{2}. This step-by-step approach ensures that each part of the process is clear and manageable, leading to a thorough understanding of how to simplify similar expressions.
Prime Factorization of 18
Prime factorization is the process of breaking down a composite number into its prime factors. For the number 18, we will identify its prime factors step by step. Prime factors are the prime numbers that multiply together to give the original number.
Let's go through the prime factorization of 18:
- Start with the Smallest Prime Number: Begin by dividing 18 by the smallest prime number, which is 2. Since 18 is even, it is divisible by 2.
- 18 ÷ 2 = 9
- Continue with the Quotient: Now, take the quotient (9) and check for the next smallest prime number, which is 3.
- 9 ÷ 3 = 3
- Repeat the Process: Repeat the division with the quotient (3) by the smallest prime number that is applicable.
- 3 ÷ 3 = 1
- Complete the Factorization: When the quotient becomes 1, the factorization process is complete. The prime factors of 18 are all the prime numbers we used in the division:
- 18 = 2 × 3 × 3
We can express this factorization using exponents to indicate repeated factors:
- 18 = 2 × 3^2
Understanding the prime factorization of 18 helps in various mathematical operations, such as simplifying square roots. For instance, knowing that 18 = 2 \times 3^2 allows us to simplify \sqrt{18} more efficiently by identifying and working with its prime factors.
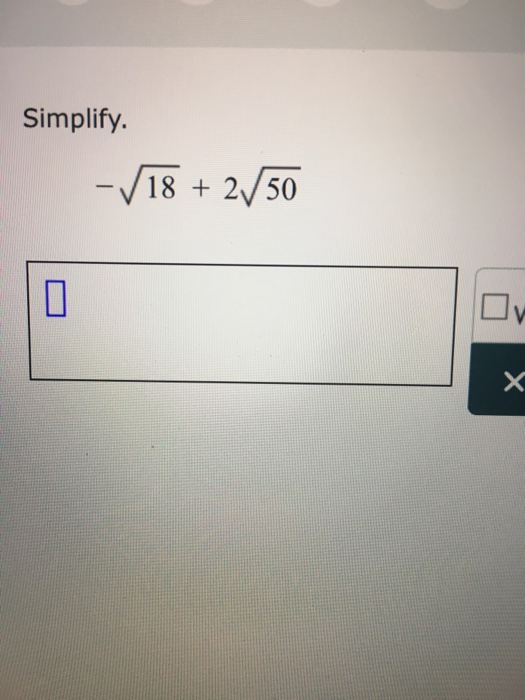
Simplifying Square Roots Involving Perfect Squares
Simplifying square roots, especially those involving perfect squares, is a useful mathematical skill. Perfect squares are numbers that can be expressed as the product of an integer with itself, such as 1, 4, 9, 16, 25, etc. Simplifying square roots involving perfect squares can make calculations easier and more intuitive.
Let's go through the process step-by-step, using the expression \sqrt{18} as an example:
- Identify the Number Inside the Square Root: In this case, the number is 18.
- Factorize the Number: Break down 18 into its prime factors. We have:
- 18 = 2 × 3 × 3 or 18 = 2 × 32
- Rewrite the Square Root: Express the square root in terms of its prime factors:
- \(\sqrt{18} = \sqrt{2 \times 3^2}\)
- Separate the Perfect Square: Recognize that \(3^2\) is a perfect square. Separate the square root into two parts:
- \(\sqrt{18} = \sqrt{2} \times \sqrt{3^2}\)
- Simplify the Square Root of the Perfect Square: Simplify \(\sqrt{3^2}\) to its integer value:
- \(\sqrt{3^2} = 3\)
- Combine the Results: Multiply the simplified integer with the remaining square root:
- \(\sqrt{18} = 3 \sqrt{2}\)
This step-by-step method can be applied to any square root expression involving perfect squares. By breaking down the number into its prime factors and isolating the perfect squares, you can simplify the square root to a more manageable form.
Using this approach, the original expression 2 \sqrt{18} can also be simplified:
- \(2 \sqrt{18} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}\)
Simplifying square roots involving perfect squares not only helps in solving equations more efficiently but also enhances your understanding of fundamental mathematical concepts.
Combining Simplified Factors
Once we have simplified the individual components of a square root expression, the next step is to combine these factors effectively. This process ensures that the expression is as simple and clear as possible. Let's use the example of 2 \sqrt{18} to illustrate this process.
- Start with the Simplified Square Root: From the previous steps, we know that:
- \(\sqrt{18} = 3 \sqrt{2}\)
- Include the Coefficient: The original expression has a coefficient 2 outside the square root. Multiply this coefficient by the simplified square root:
- \(2 \sqrt{18} = 2 \times 3 \sqrt{2}\)
- Perform the Multiplication: Multiply the coefficients (numbers outside the square root):
- \(2 \times 3 = 6\)
- Combine the Results: After performing the multiplication, combine the result with the remaining square root part:
- \(2 \sqrt{18} = 6 \sqrt{2}\)
Thus, the expression 2 \sqrt{18} simplifies to 6 \sqrt{2}. This process of combining simplified factors involves careful multiplication and ensuring that all parts of the expression are accounted for correctly.
Understanding how to combine simplified factors is essential for simplifying complex expressions in mathematics. It allows you to transform unwieldy expressions into more manageable forms, making calculations easier and more intuitive.
Final Multiplication and Simplification
After breaking down the components of the expression 2 \sqrt{18} and simplifying the square root, the final step involves performing the multiplication and achieving the simplest form of the expression. Let's walk through this process step-by-step:
- Simplify the Square Root: From our previous steps, we know that:
- \(\sqrt{18} = 3 \sqrt{2}\)
- Include the Coefficient: The original expression has a coefficient of 2 outside the square root. Therefore, the expression becomes:
- \(2 \sqrt{18} = 2 \times 3 \sqrt{2}\)
- Multiply the Coefficients: Multiply the coefficient 2 by the simplified factor 3:
- \(2 \times 3 = 6\)
- Combine the Results: Finally, combine the coefficient with the remaining square root part:
- \(2 \sqrt{18} = 6 \sqrt{2}\)
Thus, the expression 2 \sqrt{18} simplifies to 6 \sqrt{2}. This final step ensures that the expression is fully simplified and ready for use in further calculations or applications.
The process of final multiplication and simplification involves careful attention to each component of the expression. By methodically combining the simplified factors and performing the necessary multiplications, we arrive at a concise and simplified result. Mastering these steps allows for efficient handling of similar expressions in mathematics.
Common Mistakes to Avoid
When simplifying expressions involving square roots, it is essential to avoid common mistakes that can lead to incorrect results. Below are some typical errors and tips on how to avoid them:
-
Incorrectly Simplifying Square Roots:
A common mistake is not fully simplifying the square root of a number. For example, in the expression \(2 \sqrt{18}\), make sure to simplify \(\sqrt{18}\) properly:
- Prime factorize the number under the square root: \(18 = 2 \times 3^2\).
- Simplify the square root by taking out the perfect square: \(\sqrt{18} = \sqrt{2 \times 3^2} = 3 \sqrt{2}\).
- Combine the simplified root with the coefficient: \(2 \sqrt{18} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}\).
-
Forgetting to Multiply the Coefficient:
When simplifying, don't forget to multiply the coefficient outside the square root by the simplified value inside. For instance:
If you simplify \(\sqrt{18}\) to \(3 \sqrt{2}\), ensure you multiply the \(2\) outside the square root:
\(2 \sqrt{18} = 2 \times 3 \sqrt{2} = 6 \sqrt{2}\).
-
Confusing Multiplication and Addition:
Another frequent mistake is confusing multiplication with addition. Remember that you multiply the coefficients and simplify the radicals separately:
\(2 \sqrt{18} = 2 \times \sqrt{18}\), not \(2 + \sqrt{18}\).
-
Incorrect Prime Factorization:
Ensure the prime factorization is done correctly. Mistakes in factorizing can lead to incorrect simplification:
For \(18\), the correct prime factorization is \(2 \times 3^2\). Using incorrect factors will result in wrong simplification.
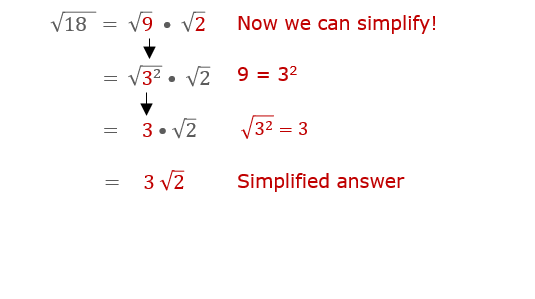
Practical Applications of Simplified Radicals
Simplifying radicals, such as the expression \(2\sqrt{18}\), has numerous practical applications across various fields. Understanding these applications can illustrate the relevance and importance of these mathematical concepts beyond the classroom.
-
Architecture and Design:
In architecture, accurate calculations are essential for designing structures. Simplified radicals can help determine dimensions and materials needed for construction projects. For instance, \(2\sqrt{18}\) simplifies to \(6\sqrt{2}\), which might represent specific measurements for structural components.
-
Physics and Engineering:
In physics, especially mechanics and optics, simplified radicals are used to calculate forces, distances, and other properties. For example, the simplified form of \(2\sqrt{18}\) can be used in equations to determine precise values necessary for engineering designs.
-
Computer Science:
In computer science, algorithms involving geometric calculations, such as graphics rendering or machine learning, often utilize simplified expressions like \(2\sqrt{18}\) for efficient computation. Simplifying these expressions ensures more efficient processing and storage.
-
Finance:
Financial analysts might use simplified radicals when calculating compound interest or other financial models. Simplifying expressions like \(2\sqrt{18}\) can help in developing more accurate financial predictions and analyses.
-
Education:
Teaching the simplification of radicals helps students understand mathematical concepts that are essential for solving real-world problems. By practicing with examples like \(2\sqrt{18}\), students learn the importance of accurate calculations in various contexts.
These examples highlight that the simplification of radicals, including expressions like \(2\sqrt{18}\), is not merely an academic exercise but a valuable tool used in various professional fields to solve real-world problems effectively and accurately.
Frequently Asked Questions (FAQ)
Here are some common questions and answers about simplifying the expression \(2 \sqrt{18}\) and working with radicals:
-
What is the simplified form of \(2 \sqrt{18}\)?
The simplified form is \(6 \sqrt{2}\). This is because \( \sqrt{18} \) can be broken down into \( \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3 \sqrt{2} \), and then multiplying by 2 gives \(2 \times 3 \sqrt{2} = 6 \sqrt{2}\).
-
Can the square root of a number be negative?
Yes, every positive number has two square roots: a positive one (the principal root) and a negative one. For example, the square roots of 16 are 4 and -4.
-
Why do we simplify square roots?
Simplifying square roots makes it easier to work with them in equations and can help to reveal underlying properties of the numbers involved. Simplified forms are usually preferred in mathematical expressions for clarity and brevity.
-
How do you simplify square roots?
To simplify a square root, you factor the number inside the square root into its prime factors, group the factors into pairs, and then take the square root of the pairs. For instance, to simplify \( \sqrt{18} \), you factor 18 into \(2 \times 3^2\), then take the square root of \(3^2\) to get 3, so \( \sqrt{18} = 3 \sqrt{2}\).
-
What are some common mistakes to avoid when simplifying square roots?
- Not fully factoring the number inside the square root.
- Incorrectly combining the coefficients outside the square root with the simplified root.
- Forgetting to include both the positive and negative roots when solving equations involving square roots.
-
What are the applications of simplified radicals in real life?
Simplified radicals are used in various fields including engineering, physics, and computer science for calculations involving wave functions, distances in coordinate systems, and optimization problems.
Conclusion and Summary
In this guide, we explored the process of simplifying the expression \(2\sqrt{18}\) through various mathematical steps and principles. The key takeaways include:
- Understanding the basics of square roots and their properties.
- Breaking down the expression \(2\sqrt{18}\) by using prime factorization to identify perfect squares within the radicand.
- Applying the simplification steps to express \( \sqrt{18} \) as \( \sqrt{9 \times 2} = 3\sqrt{2} \), and then multiplying by the coefficient to get \(2 \times 3\sqrt{2} = 6\sqrt{2}\).
- Recognizing common mistakes such as incorrect factorization and misapplication of square root properties.
- Understanding practical applications of simplified radicals in fields like engineering, physics, and real-world problem solving, where precise measurements and calculations are essential.
By mastering these steps and avoiding common pitfalls, you can simplify square root expressions accurately and efficiently. The knowledge gained from this guide not only helps in academic contexts but also in various practical applications, enhancing your overall mathematical proficiency.
Một Vấn Đề Căn Bậc Hai Hay ✓18+✓8=?
READ MORE:
Cách Đơn Giản Hóa Căn Bậc Hai của 18: √18