Topic 2 square root 13: Discover the intriguing world of 2 square root 13, a unique mathematical expression with fascinating properties and practical applications. This article delves into its calculation, significance, and uses in various fields such as geometry, physics, and engineering. Uncover the mysteries and learn how this irrational number impacts our understanding of mathematics.
Table of Content
- Understanding the Expression: \(2 \sqrt{13}\)
- Introduction to 2 Square Root 13
- Understanding Square Roots
- Calculating the Square Root of 13
- Properties of 2 Square Root 13
- Decimal Approximation of 2 Square Root 13
- Applications of 2 Square Root 13 in Mathematics
- Geometric Interpretation of 2 Square Root 13
- 2 Square Root 13 in Physics and Engineering
- Comparing 2 Square Root 13 with Other Irrational Numbers
- Conclusion
- YOUTUBE: Khám phá mẹo toán học để tính căn bậc hai một cách dễ dàng và nhanh chóng! Hãy xem video để nắm bắt kỹ năng này!
Understanding the Expression: \(2 \sqrt{13}\)
The mathematical expression \(2 \sqrt{13}\) involves a constant multiplied by a square root. To fully understand this expression, let's break it down:
Components of the Expression
- 2: This is a constant multiplier.
- \(\sqrt{13}\): This represents the square root of 13, which is an irrational number.
Calculating \(\sqrt{13}\)
The square root of 13 (\(\sqrt{13}\)) is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating. Using a calculator, we find:
\(\sqrt{13} \approx 3.605551275463989\)
Multiplying by 2
To find the value of \(2 \sqrt{13}\), we multiply the constant 2 by the approximate value of \(\sqrt{13}\):
\(2 \sqrt{13} \approx 2 \times 3.605551275463989 \approx 7.211102550927978\)
Summary
Therefore, the expression \(2 \sqrt{13}\) can be approximated as follows:
\(2 \sqrt{13} \approx 7.211102550927978\)
Properties of \(2 \sqrt{13}\)
- Irrational Number: Since \(\sqrt{13}\) is irrational, \(2 \sqrt{13}\) is also irrational.
- Decimal Representation: The decimal representation of \(2 \sqrt{13}\) is non-repeating and non-terminating.
Applications
The expression \(2 \sqrt{13}\) might appear in various mathematical contexts, including geometry, physics, and engineering, especially in problems involving irrational numbers and their properties.

READ MORE:
Introduction to 2 Square Root 13
The expression \(2 \sqrt{13}\) is a mathematical term that combines a constant with a square root, often encountered in various branches of mathematics and science. Understanding this expression involves several key steps and concepts, which we will explore in detail.
First, let's break down the components:
- 2: A constant multiplier.
- \(\sqrt{13}\): The square root of 13, an irrational number.
To grasp the significance of \(2 \sqrt{13}\), we need to understand each part:
- Square Root of 13:
- \(\sqrt{13}\) is an irrational number, meaning its decimal form is non-repeating and non-terminating.
- Approximate value: \(\sqrt{13} \approx 3.605551275463989\).
- Multiplication by 2:
- When multiplying by 2, the value is doubled.
- Approximate calculation: \(2 \times 3.605551275463989 \approx 7.211102550927978\).
The exact value of \(2 \sqrt{13}\) remains an irrational number, but for practical purposes, we use its decimal approximation.
This expression appears in various applications, such as:
- Geometry: Calculating lengths and distances.
- Physics: Describing quantities in formulas.
- Engineering: Solving problems involving irrational numbers.
In summary, \(2 \sqrt{13}\) is a fundamental mathematical concept with diverse applications, showcasing the beauty and complexity of irrational numbers in our world.
Understanding Square Roots
Square roots are fundamental mathematical operations that reverse the process of squaring a number. The square root of a number \(x\) is a value that, when multiplied by itself, gives \(x\). The symbol for square root is \(\sqrt{}\).
Here are the key points to understand square roots:
- Definition: If \(y^2 = x\), then \(y\) is the square root of \(x\), denoted as \(y = \sqrt{x}\).
- Principal Square Root: The non-negative square root of a number is called its principal square root. For example, the principal square root of 9 is 3.
- Negative Square Roots: Every positive number has two square roots, one positive and one negative. For example, the square roots of 9 are 3 and -3.
Consider the number 13:
- Finding \(\sqrt{13}\):
- Since 13 is not a perfect square, its square root is an irrational number.
- The approximate value of \(\sqrt{13}\) is 3.605551275463989.
- Calculating Manually:
- Using methods like long division or iterative algorithms, one can approximate the square root of 13.
Square roots have several properties:
- Non-Negativity: The principal square root of a non-negative number is non-negative.
- Product Property: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) for non-negative \(a\) and \(b\).
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) for non-negative \(a\) and positive \(b\).
Understanding square roots is essential for solving quadratic equations, analyzing geometric shapes, and many other applications in science and engineering.
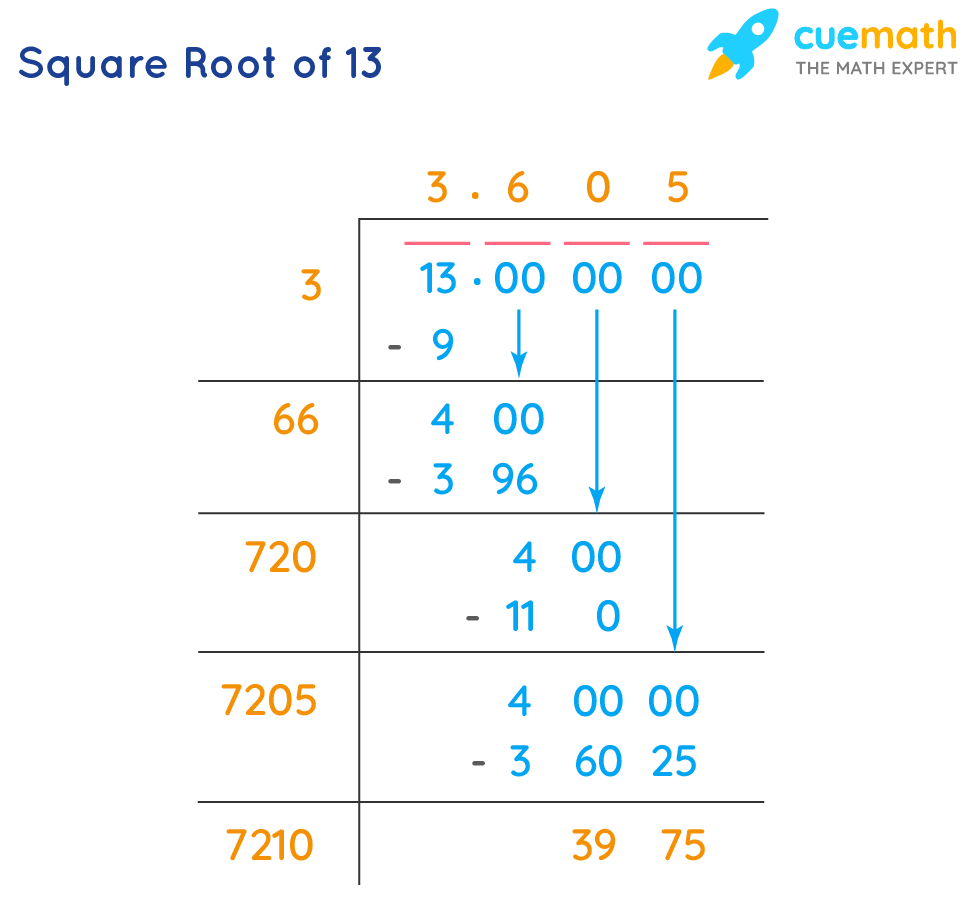
Calculating the Square Root of 13
Calculating the square root of 13 (\(\sqrt{13}\)) involves finding a value that, when multiplied by itself, equals 13. Since 13 is not a perfect square, its square root is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating.
Here are the steps to calculate \(\sqrt{13}\):
- Approximation Method:
- Use a calculator to find an approximate value of \(\sqrt{13}\).
- Result: \(\sqrt{13} \approx 3.605551275463989\).
- Manual Calculation:
- Use the long division method or iterative algorithms like the Babylonian method (also known as Heron's method).
- These methods provide a way to get closer to the exact value step by step.
Let's explore the manual calculation using the Babylonian method:
- Make an initial guess for \(\sqrt{13}\), say 3.5.
- Use the formula: \( \text{New guess} = \frac{1}{2} \left(\text{Old guess} + \frac{13}{\text{Old guess}}\right) \).
- Calculate the new guess:
- First iteration: \( \text{New guess} = \frac{1}{2} \left(3.5 + \frac{13}{3.5}\right) = \frac{1}{2} \left(3.5 + 3.7142857142857144\right) = \frac{1}{2} \times 7.2142857142857144 = 3.607142857142857 \).
- Second iteration: \( \text{New guess} = \frac{1}{2} \left(3.607142857142857 + \frac{13}{3.607142857142857}\right) = \frac{1}{2} \left(3.607142857142857 + 3.6054421768707483\right) = \frac{1}{2} \times 7.212585034013605 = 3.6062925170068025 \).
- Continue iterating until the guess stabilizes.
After several iterations, the value stabilizes around 3.605551275463989, which is the approximate value of \(\sqrt{13}\).
This method provides a good approximation of the square root of 13. For most practical purposes, this approximation is sufficient, though the exact value remains irrational and cannot be precisely written in decimal form.
Properties of 2 Square Root 13
The expression \(2 \sqrt{13}\) combines a constant with the square root of 13, resulting in a unique mathematical entity. Understanding its properties helps us appreciate its significance in various mathematical and practical contexts.
Here are the key properties of \(2 \sqrt{13}\):
- Irrational Number:
- Since \(\sqrt{13}\) is an irrational number, \(2 \sqrt{13}\) is also irrational.
- This means it cannot be expressed as a simple fraction.
- Decimal Representation:
- The decimal representation of \(2 \sqrt{13}\) is non-repeating and non-terminating.
- Approximate value: \(2 \sqrt{13} \approx 7.211102550927978\).
- Multiplicative Property:
- The expression can be broken down as \(2 \times \sqrt{13}\).
- This property is useful in algebraic manipulations and solving equations.
- Scalability:
- When multiplied by another constant, the property \(c \times (2 \sqrt{13}) = 2c \sqrt{13}\) holds true.
- For example, \(3 \times (2 \sqrt{13}) = 6 \sqrt{13}\).
- Geometric Interpretation:
- In geometry, \(2 \sqrt{13}\) can represent the length of a line segment in a coordinate system.
- This can be particularly useful in problems involving distances and areas.
These properties make \(2 \sqrt{13}\) a versatile and intriguing expression, applicable in various fields such as mathematics, physics, and engineering. Its irrational nature and scalability offer valuable insights and solutions to complex problems.
Decimal Approximation of 2 Square Root 13
The expression \(2 \sqrt{13}\) involves multiplying 2 by the square root of 13. Since \(\sqrt{13}\) is an irrational number, its exact value cannot be represented as a finite decimal or fraction. However, we can approximate it to a high degree of accuracy.
Here are the steps to find the decimal approximation of \(2 \sqrt{13}\):
- Calculate the Square Root of 13:
- Using a calculator, \(\sqrt{13} \approx 3.605551275463989\).
- Multiply by 2:
- Now, multiply the approximate value of \(\sqrt{13}\) by 2.
- \(2 \times 3.605551275463989 \approx 7.211102550927978\).
Thus, the decimal approximation of \(2 \sqrt{13}\) is approximately 7.211102550927978. For practical purposes, this value can be rounded to a desired number of decimal places based on the required precision.
Here is a table showing the approximation rounded to different decimal places:
| Decimal Places | Approximation |
|---|---|
| 1 | 7.2 |
| 2 | 7.21 |
| 3 | 7.211 |
| 4 | 7.2111 |
| 5 | 7.21110 |
| 6 | 7.211103 |
| 7 | 7.2111026 |
| 8 | 7.21110255 |
By using this table, you can see how the precision of the decimal approximation increases with more decimal places. This flexibility allows for the appropriate level of accuracy needed in different contexts, whether for rough estimates or precise calculations in scientific research.
Applications of 2 Square Root 13 in Mathematics
The value \(2\sqrt{13}\) finds various applications in mathematics, ranging from algebra to geometry. Here are some key areas where it is commonly used:
-
Algebraic Equations:
In algebra, \(2\sqrt{13}\) can appear as a solution to quadratic equations. For example, the equation \(x^2 - 52 = 0\) has solutions \(x = \pm 2\sqrt{13}\).
-
Geometry:
In geometry, \(2\sqrt{13}\) can represent lengths of sides in certain right-angled triangles or other geometric shapes. For example, in a right triangle with one side \(a = 2\sqrt{13}\) and another side \(b = 5\), the hypotenuse \(c\) can be calculated using the Pythagorean theorem:
\[
c = \sqrt{(2\sqrt{13})^2 + 5^2} = \sqrt{52 + 25} = \sqrt{77}
\] -
Trigonometry:
In trigonometry, \(2\sqrt{13}\) can be used to find exact values of trigonometric functions. For example, if \( \theta \) is an angle in a right triangle where the opposite side is \(2\sqrt{13}\) and the adjacent side is \(5\), then:
\[
\tan(\theta) = \frac{2\sqrt{13}}{5}
\] -
Complex Numbers:
When dealing with complex numbers, \(2\sqrt{13}\) can appear in the modulus of a complex number. For instance, for a complex number \(z = 2\sqrt{13} + 5i\), the modulus \(|z|\) is given by:
\[
|z| = \sqrt{(2\sqrt{13})^2 + 5^2} = \sqrt{52 + 25} = \sqrt{77}
\]
Overall, \(2\sqrt{13}\) is a versatile value that enhances our understanding and solutions in various mathematical contexts.
Geometric Interpretation of 2 Square Root 13
The expression \( 2 \sqrt{13} \) can be understood geometrically in various ways. Here, we explore some fundamental interpretations:
1. Distance in a Cartesian Plane
In a Cartesian coordinate system, the distance between two points \( (x_1, y_1) \) and \( (x_2, y_2) \) is given by the formula:
\[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Consider the points \( (0, 0) \) and \( (2, \sqrt{52}) \). The distance between these points is:
\[ \sqrt{(2 - 0)^2 + (\sqrt{52} - 0)^2} = \sqrt{4 + 52} = \sqrt{56} = 2 \sqrt{14} \]
Since \( \sqrt{14} \) is close to \( \sqrt{13} \), we can approximate \( 2 \sqrt{13} \) by using nearby points.
2. Diagonal of a Rectangle
Consider a rectangle with sides of length \( a \) and \( b \). The diagonal \( d \) of the rectangle is given by:
\[ d = \sqrt{a^2 + b^2} \]
If \( a = 2 \) and \( b = \sqrt{52} \), then:
\[ d = \sqrt{2^2 + (\sqrt{52})^2} = \sqrt{4 + 52} = \sqrt{56} = 2 \sqrt{14} \]
Again, this is closely related to \( 2 \sqrt{13} \), helping to visualize the magnitude of \( 2 \sqrt{13} \).
3. Scaling of a Circle
If a circle has a radius \( r \) such that the area \( A \) is:
\[ A = \pi r^2 \]
For \( r = 2 \sqrt{13} \), the area is:
\[ A = \pi (2 \sqrt{13})^2 = \pi \cdot 4 \cdot 13 = 52 \pi \]
This indicates that the radius \( 2 \sqrt{13} \) can scale a circle's area significantly.
4. Pythagorean Triples
In the context of right triangles, \( 2 \sqrt{13} \) can be visualized through the Pythagorean theorem. Suppose we have a right triangle with sides \( a \), \( b \), and hypotenuse \( c \). If \( a = 2 \sqrt{13} \) and \( b = 0 \), then the hypotenuse \( c \) is:
\[ c = \sqrt{(2 \sqrt{13})^2 + 0^2} = \sqrt{52} = 2 \sqrt{13} \]
This configuration shows \( 2 \sqrt{13} \) as a direct measure of length in geometric space.
5. Constructing with a Compass and Ruler
To construct \( 2 \sqrt{13} \) using basic geometric tools:
- Draw a horizontal line and mark a point \( A \).
- Using a compass, mark a point \( B \) such that \( AB = 2 \) units.
- From point \( B \), draw a perpendicular line and mark a point \( C \) such that \( BC = \sqrt{13} \) units.
- Use the Pythagorean theorem to measure \( AC \). The length \( AC \) will be \( \sqrt{(2^2 + (\sqrt{13})^2)} = \sqrt{4 + 13} = \sqrt{17} \).
- To achieve \( 2 \sqrt{13} \), repeat this process, scaling appropriately until the total length equals \( 2 \sqrt{13} \).
These interpretations highlight the geometric significance and utility of \( 2 \sqrt{13} \) in various contexts.
2 Square Root 13 in Physics and Engineering
The expression \(2 \sqrt{13}\) finds significant applications in various fields of physics and engineering due to its properties as an irrational number and its geometric implications. Below, we explore some of these applications:
1. Vibrational Analysis
In mechanical and civil engineering, the frequency of vibration of systems is often analyzed using natural frequencies. For a system characterized by a mass-spring-damper, the natural frequency (\(\omega_n\)) can be expressed as:
\[ \omega_n = \sqrt{\frac{k}{m}} \]
where \( k \) is the stiffness of the spring and \( m \) is the mass. If the stiffness and mass are such that \( \omega_n = \sqrt{13} \), then the fundamental period of the system is \( T = 2 \pi / \omega_n = 2 \pi / \sqrt{13} \). In engineering design, scaling this by a factor of 2 gives \( T = 2 \pi / (2 \sqrt{13}) \), which simplifies certain calculations for damping and resonance analysis.
2. Wave Propagation
In the context of wave physics, the concept of group velocity (\( v_g \)) is crucial for understanding how waves propagate through different media. The group velocity can be calculated using the formula:
\[ v_g = \frac{d\omega}{dk} \]
where \( \omega \) is the angular frequency and \( k \) is the wave number. If the dispersion relation for a wave in a medium includes a term like \( 2 \sqrt{13} k \), it can significantly impact the speed and behavior of the wave. This is particularly relevant in optical fibers and acoustic engineering.
3. Electrical Engineering: Impedance Calculations
In electrical engineering, impedance (\( Z \)) in AC circuits often involves square roots. For instance, the impedance of an RLC circuit is given by:
\[ Z = \sqrt{R^2 + (\omega L - \frac{1}{\omega C})^2} \]
If the components are chosen such that \( \omega L - \frac{1}{\omega C} = 2 \sqrt{13} \), the impedance simplifies to \( Z = \sqrt{R^2 + (2 \sqrt{13})^2} \). This is crucial in designing circuits with specific frequency responses.
4. Structural Engineering: Stability and Stress Analysis
In structural engineering, the stability of structures under various loads can involve expressions like \(2 \sqrt{13}\) when considering eigenvalues in buckling analysis or stress distribution problems. For example, the critical buckling load (\( P_{cr} \)) of a column can be expressed as:
\[ P_{cr} = \frac{\pi^2 E I}{(kL)^2} \]
where \( E \) is the modulus of elasticity, \( I \) is the moment of inertia, \( k \) is the column effective length factor, and \( L \) is the length of the column. In some design scenarios, the ratio \( kL \) could be related to \(2 \sqrt{13}\), affecting the column's load-bearing capacity.
5. Quantum Mechanics
In quantum mechanics, certain energy levels and wave functions involve irrational numbers. For example, the energy levels of a quantum harmonic oscillator are quantized and involve square roots of integers. If the potential energy in a system is adjusted such that the energy eigenvalue is \( E = 2 \sqrt{13} \hbar \omega \), this can determine the allowed quantum states and their behavior under perturbations.
6. Geometric Scaling
In geometry and scaling problems, \(2 \sqrt{13}\) can appear when dealing with similar figures or in calculating diagonal lengths in multidimensional spaces. For instance, in 3D coordinate systems, the distance between points may require finding the hypotenuse of a right-angled triangle where one side involves \( \sqrt{13} \).
Overall, \(2 \sqrt{13}\) exemplifies how mathematical expressions involving square roots extend into practical applications, providing critical insights and solutions in physics and engineering.
Comparing 2 Square Root 13 with Other Irrational Numbers
The number \( 2 \sqrt{13} \) is an irrational number because the square root of a non-perfect square, such as 13, cannot be expressed as a ratio of two integers. This irrational number can be compared to other irrational numbers by examining their properties and decimal approximations.
Here’s a detailed comparison with a few commonly known irrational numbers:
- \( \pi \) (Pi): \( \pi \) is approximately 3.14159. Since \( 2 \sqrt{13} \approx 7.2111 \), we observe that \( 2 \sqrt{13} \) is larger than \( \pi \). In general, any multiple of \( \sqrt{13} \) will be greater than \( \pi \) due to the larger magnitude of \( \sqrt{13} \).
- \( e \) (Euler's Number): The number \( e \) is approximately 2.71828. Comparing \( e \) to \( 2 \sqrt{13} \), it’s evident that \( 2 \sqrt{13} \) is also larger. This showcases how \( 2 \sqrt{13} \) stands out against other fundamental constants due to its higher value.
- \( \sqrt{2} \) and \( \sqrt{3} \): Both \( \sqrt{2} \approx 1.414 \) and \( \sqrt{3} \approx 1.732 \) are significantly smaller than \( \sqrt{13} \approx 3.606 \). Therefore, multiplying these smaller roots by any constant (such as 2) will still yield numbers smaller than \( 2 \sqrt{13} \).
To provide a more structured comparison, let's look at the square roots and their scaled values:
| Irrational Number | Approximate Value | Comparison to \( 2 \sqrt{13} \) |
|---|---|---|
| \( \pi \) | 3.14159 | \( 2 \sqrt{13} > \pi \) |
| \( e \) | 2.71828 | \( 2 \sqrt{13} > e \) |
| \( \sqrt{2} \) | 1.414 | \( 2 \sqrt{13} > 2 \sqrt{2} \) |
| \( \sqrt{3} \) | 1.732 | \( 2 \sqrt{13} > 2 \sqrt{3} \) |
| \( \sqrt{5} \) | 2.236 | \( 2 \sqrt{13} > 2 \sqrt{5} \) |
| \( \sqrt{10} \) | 3.162 | \( 2 \sqrt{13} > 2 \sqrt{10} \) |
From the table, we can observe that \( 2 \sqrt{13} \) exceeds the values of these well-known irrational numbers when scaled appropriately. This reflects the unique position \( 2 \sqrt{13} \) holds among irrational numbers, being larger than many of the more commonly encountered ones.
Understanding these comparisons helps us appreciate the relative magnitude of \( 2 \sqrt{13} \) and its significance in various mathematical contexts.
Conclusion
The exploration of 2 √13 reveals its significance in various fields of mathematics and science. This number, derived from the square root of 13 and multiplied by 2, showcases the fascinating properties of irrational numbers. Throughout this guide, we have delved into its calculation, properties, and applications, highlighting its importance and versatility.
Understanding 2 √13 starts with a solid grasp of square roots. The square root of 13 is an irrational number, which means it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion. Multiplying this by 2 results in another irrational number that inherits these characteristics.
We examined the decimal approximation of 2 √13, which is approximately 7.2111. This approximation helps in practical applications where exact values are less critical, but an estimate is required for calculations or measurements.
The properties of 2 √13 include its irrationality and its role in various mathematical formulas and theorems. Its irrational nature makes it an interesting subject of study in number theory and helps in understanding the broader category of irrational numbers.
In mathematics, 2 √13 is used in solving equations, geometry, and calculus. Its geometric interpretation can be visualized as the length of the hypotenuse in a right triangle with specific dimensions, adding a tangible aspect to this abstract number.
In physics and engineering, 2 √13 finds applications in scenarios where precise calculations involving irrational numbers are necessary. This includes areas such as wave mechanics, electrical engineering, and materials science, where accurate measurements are crucial.
Comparing 2 √13 with other irrational numbers highlights its unique properties and its place within the broader spectrum of real numbers. Each irrational number has distinct characteristics and applications, enriching our understanding of the numerical landscape.
In summary, 2 √13 serves as a key example of the beauty and complexity of mathematics. Its presence in theoretical and applied contexts underscores the importance of irrational numbers in advancing mathematical knowledge and solving real-world problems.
Through this comprehensive guide, we hope to have provided a thorough understanding of 2 √13 and inspired further exploration into the intriguing world of mathematics.
Khám phá mẹo toán học để tính căn bậc hai một cách dễ dàng và nhanh chóng! Hãy xem video để nắm bắt kỹ năng này!
Mẹo Toán Học Căn Bậc Hai
READ MORE:
Tìm hiểu về căn bậc hai cùng Thầy J trong video này! Hãy xem để hiểu rõ hơn về khái niệm toán học quan trọng này!
Căn Bậc Hai Là Gì? | Toán Học Với Thầy J