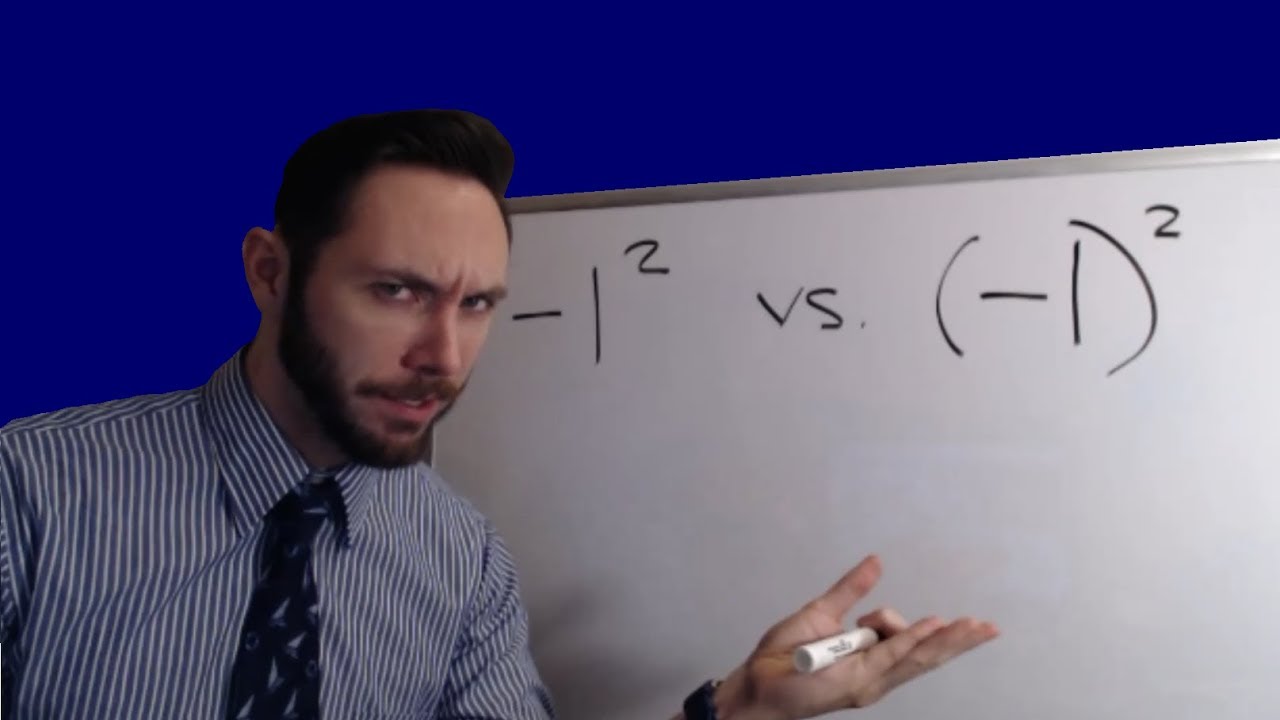Topic what is x squared squared: The concept of "x squared squared" can be intriguing for both math enthusiasts and learners. When you square a squared term, like x squared, you get x to the fourth power, written as \( x^4 \). This idea extends beyond basic algebra and has numerous applications in higher mathematics and real-world scenarios. Explore this article to gain a comprehensive understanding of this mathematical concept.
Table of Content
Understanding x Squared Squared
The concept of "x squared squared" refers to taking the square of a variable x, and then squaring the result. In mathematical terms, this can be expressed as follows:
- First, we square x, which is represented as \(x^2\).
- Next, we square the result of \(x^2\), leading to \((x^2)^2\).
This can be simplified using the properties of exponents:
\[
(x^2)^2 = x^{2 \times 2} = x^4
\]
Properties of Squaring and Its Applications
Understanding the operation of squaring is fundamental in various areas of mathematics:
- Quadratic Equations: Squaring forms the basis for quadratic equations, which are polynomial equations of the second degree, typically written as \(ax^2 + bx + c = 0\).
- Geometry: In geometry, squaring is used to calculate the area of squares and to explore the properties of parabolas, the graphs of quadratic functions.
- Algebra: Squaring numbers and variables is a key operation in algebra, essential for solving equations and understanding polynomial expressions.
Examples of Squaring in Equations
Here are some examples illustrating the concept of squaring and its application:
| Expression | Squared Result | Explanation |
|---|---|---|
| x | x^2 | The variable x is multiplied by itself. |
| x^2 | x^4 | The square of x is squared again, resulting in \(x^4\). |
| x^2 + x^2 | 2x^2 | The sum of x squared plus x squared is \(2x^2\), demonstrating the addition of like terms. |
Conclusion
In conclusion, the operation of squaring is a foundational concept in mathematics that extends to various fields such as algebra, geometry, and calculus. The expression "x squared squared" simplifies to \(x^4\), showcasing the power of exponentiation in mathematical operations and problem-solving.

READ MORE:
Introduction
Understanding the concept of squaring numbers is fundamental in mathematics. When a number is squared, it is multiplied by itself. The term "x squared squared" refers to raising x to the power of 4, or (x^2)^2 = x^4. This concept is crucial in algebra and has various applications in geometry, calculus, and other areas of mathematics. In this section, we will explore the definition, properties, and applications of squaring numbers, providing a solid foundation for further mathematical learning.
What is X Squared?
The expression x squared, denoted as \(x^2\), refers to the mathematical operation where a number or variable \(x\) is multiplied by itself. This fundamental concept is a cornerstone in various branches of mathematics, including algebra, geometry, and calculus.
In algebra, \(x^2\) forms the basis for quadratic equations, which are equations of the form \(ax^2 + bx + c = 0\). These equations often describe parabolic graphs and are essential in solving many real-world problems, such as calculating projectile trajectories.
Understanding \(x^2\) also plays a crucial role in geometry, particularly in determining the area of squares. For a square with side length \(x\), the area is given by \(x^2\). This geometric interpretation is where the term "squared" originates.
To summarize, \(x\) represents a number that hasn't been manipulated, while \(x^2\) signifies that \(x\) is being multiplied by itself. This operation significantly impacts the behavior of equations and their graphs, transitioning from linear equations with straight-line graphs to quadratic equations with parabolic graphs.
Additionally, in more advanced mathematics, understanding the properties and behavior of \(x^2\) lays the foundation for exploring higher-degree polynomials, complex numbers, and various calculus concepts.
Calculating X Squared Squared
To understand the concept of "x squared squared," we need to delve into the rules of exponents. Squaring a number means multiplying it by itself. When we square a squared number, we are essentially raising the exponent to another power.
- First, consider x squared, written as \( x^2 \).
- Next, squaring this result means multiplying \( x^2 \) by itself: \( (x^2)^2 \).
According to the rules of exponents, \( (a^m)^n = a^{m \cdot n} \). Therefore:
\[
(x^2)^2 = x^{2 \cdot 2} = x^4
\]
So, "x squared squared" is written as \( x^4 \), representing x raised to the fourth power.
Importance in Mathematics
The concept of squaring a number, denoted as \( x^2 \), is fundamental in mathematics. It is used in various fields, from basic arithmetic to advanced algebra and calculus. Squaring numbers allows for the exploration of quadratic equations, which have profound applications in science, engineering, and finance.
Here are some key points about the importance of \( x^2 \) in mathematics:
- Quadratic Equations: These equations, of the form \( ax^2 + bx + c = 0 \), are essential in algebra. They help in modeling real-world scenarios such as projectile motion and economics.
- Geometry: Squaring is used to calculate areas, particularly for squares and rectangles. For instance, the area of a square with side length \( x \) is \( x^2 \).
- Graphing: The graph of \( y = x^2 \) is a parabola, a U-shaped curve that is central to understanding various mathematical phenomena.
- Positive Values: For any real number \( x \), \( x^2 \) is always non-negative. This property is crucial for solving equations and inequalities.
- Complex Numbers: In complex number theory, squaring plays a role in defining and understanding imaginary numbers, where \( i^2 = -1 \).
Overall, \( x^2 \) is a building block for numerous mathematical concepts and techniques, making it a cornerstone of mathematical education and application.
:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)
Applications in Quadratic Equations
Quadratic equations are fundamental in mathematics and have a variety of applications. The expression \(x^2\) often appears in these equations, making the concept of \(x\) squared squared relevant. Here are some detailed applications:
- Solving Quadratic Equations: Quadratic equations often take the form \(ax^2 + bx + c = 0\). These equations can be solved using the quadratic formula, factoring, or completing the square. Understanding powers of \(x\) is essential in each method.
- Graphing Parabolas: The graph of a quadratic equation is a parabola. Knowing how to square \(x\) and how it affects the shape and direction of the parabola is crucial for accurate graphing and interpretation of the roots.
- Physics and Engineering: Quadratic equations model various physical phenomena, such as projectile motion, where the height \(h\) of an object is given by a quadratic expression in terms of time \(t\), like \(h = -4t^2 + 16t + 20\). Understanding the powers of \(x\) helps in predicting and analyzing these motions.
- Economics: Quadratic equations are used in economics to model cost functions and profit maximization problems. For example, finding the maximum profit involves solving a quadratic equation derived from the revenue and cost functions.
- Optimization Problems: Many optimization problems in mathematics require finding the maximum or minimum value of a quadratic function. These problems involve understanding the behavior of \(x^2\) terms and how they contribute to the function's overall shape.
Understanding the concept of \(x\) squared squared and its applications in quadratic equations provides a strong foundation for solving real-world problems across various fields.
Graphical Representation
Graphical representation is a visual way of presenting data and mathematical functions to make them easier to understand and interpret. This section will explain how to graphically represent the function \( (x^2)^2 \) and explore the characteristics of the resulting graph.
- Understanding the Function: The function \( (x^2)^2 \) simplifies to \( x^4 \). This is a polynomial function of degree 4.
- Graph Characteristics: The graph of \( y = x^4 \) is a U-shaped curve, similar to \( y = x^2 \), but steeper near the origin and flatter as \( x \) moves away from zero.
- Plotting the Graph:
- Identify key points such as the vertex and intercepts. The vertex of \( y = x^4 \) is at the origin (0,0).
- Choose several values for \( x \) (e.g., -2, -1, 0, 1, 2) and calculate the corresponding \( y \) values.
- Plot these points on a coordinate plane.
- Draw a smooth curve through the points, ensuring the curve is symmetrical about the y-axis.
- Interpreting the Graph:
- The function \( y = x^4 \) has even symmetry, meaning it is symmetric with respect to the y-axis.
- As \( x \) approaches infinity, \( y \) increases rapidly, demonstrating the steeper nature of the graph compared to \( y = x^2 \).
- The graph has a single minimum point at the origin, where \( x = 0 \) and \( y = 0 \).
Graphical representation of functions like \( (x^2)^2 \) helps in visualizing their behavior, understanding their properties, and interpreting their applications in various mathematical contexts.
Common Mistakes
When dealing with x squared squared, there are several common mistakes that students often make. Here we outline these errors and provide clear explanations to avoid them.
- Misunderstanding the Notation:
One common mistake is misunderstanding the notation (x2)2. This expression means squaring the result of x squared, not simply doubling the exponent.
Correct interpretation: (x2)2 = x4
- Incorrectly Applying the Exponent Rules:
Another mistake is incorrectly applying the exponent rules. Remember that (am)n = am*n.
For (x2)2, m = 2 and n = 2, so x2*2 = x4.
- Forgetting to Simplify Fully:
Sometimes, students stop at x2 * x2 instead of simplifying it to x4.
Always ensure you fully simplify the expression.
- Confusing with Addition:
Do not confuse squaring with addition. For example, (x + y)2 ≠ x2 + y2. This is known as the distributive property mistake.
Instead, use the binomial expansion: (x + y)2 = x2 + 2xy + y2.
By understanding these common mistakes and following the correct steps, you can accurately calculate and simplify x squared squared and avoid these pitfalls.
Đạo hàm trực quan của x bình phương
READ MORE:
Giải phương trình x bình phương = 4 và các giá trị bình phương khác của x