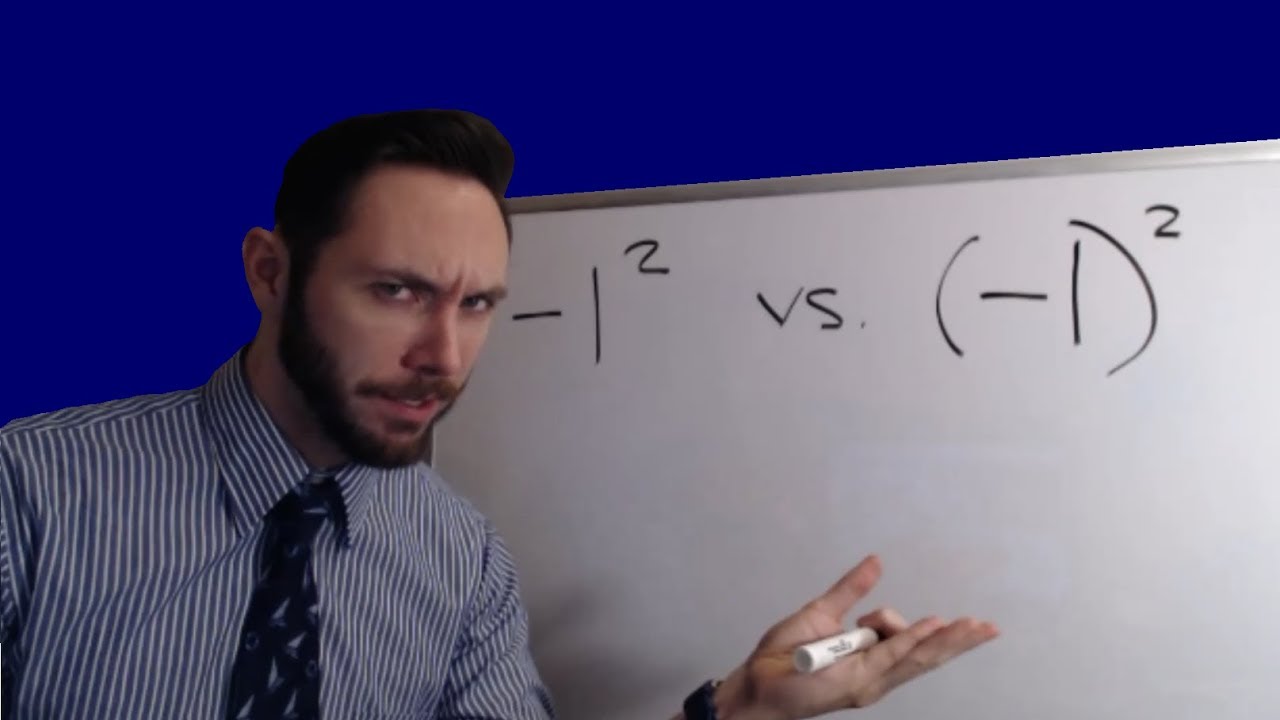What's 4 Squared? Discover the Answer and Its Importance

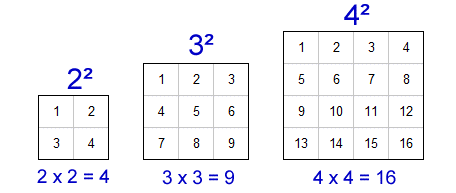
In mathematics, squaring a number means multiplying the number by itself. This operation is represented by raising the number to the power of 2.

Calculation

The expression for 4 squared is written as \( 4^2 \).

To calculate \( 4^2 \), you multiply 4 by itself:

\[
4^2 = 4 \times 4 = 16
\]

Applications

Squaring numbers is a common operation in various fields, including:

• Geometry: Calculating the area of a square.
• Algebra: Solving quadratic equations.
• Physics: Working with formulas involving square terms, such as kinetic energy.

Properties

Here are some key properties of squaring a number:

• Positive Result: The square of any real number is non-negative.
• Even Number Squared: The square of an even number is even.
• Odd Number Squared: The square of an odd number is odd.

Squaring a number is a fundamental arithmetic operation where a number is multiplied by itself. This operation is denoted using an exponent of 2. Squaring is widely used in various fields of mathematics and science, and it forms the basis for more complex concepts such as quadratic equations and geometric calculations.

Here's a step-by-step explanation of squaring a number:

• Step 1: Identify the number you want to square. For example, let's use the number 4.
• Step 2: Multiply the number by itself. This is written mathematically as \( 4 \times 4 \).
• Step 3: Calculate the product. For 4 squared, the calculation is:

  
  \[
  4^2 = 4 \times 4 = 16
  \]

The result of squaring 4 is 16. This simple operation has a wide range of applications, from calculating areas in geometry to solving problems in algebra and physics.

Understanding how to square numbers and the properties of squared numbers is essential for mastering many mathematical concepts and for practical problem-solving in everyday life.

When we talk about squaring the number 4, we are referring to the mathematical operation of raising 4 to the power of 2. This can be expressed as \( 4^2 \).

Here is a detailed, step-by-step explanation of how to understand and calculate 4 squared:

1. Identify the Base Number: In this case, the base number is 4.
2. Exponentiation: The exponent indicates how many times the base number is multiplied by itself. For 4 squared, the exponent is 2, so we multiply 4 by itself.
3. Mathematical Expression: Write the expression for squaring 4, which is:

   
   \[
   4^2
   \]

4. Perform the Multiplication: Multiply the base number by itself:

   
   \[
   4 \times 4 = 16
   \]

Therefore, 4 squared equals 16. This means that when you multiply 4 by itself, the product is 16.

Squaring numbers is not just a basic arithmetic operation but also an essential concept in various mathematical and scientific applications. For example, it is used in calculating the area of a square, solving quadratic equations, and analyzing physical phenomena.

Understanding how to square a number like 4 helps build a foundation for more advanced mathematical concepts and problem-solving skills.

Squaring a number is a basic mathematical operation that involves multiplying a number by itself. It is an example of an exponentiation operation where the exponent is 2. This operation is fundamental in arithmetic, algebra, and geometry, and it is represented using the notation \( x^2 \), where \( x \) is the base number.

Here is a detailed explanation of the mathematical definition of squaring:

• Base Number: The number to be squared is called the base. For example, in \( 4^2 \), the base number is 4.
• Exponent: The exponent in squaring is always 2, indicating that the base number is multiplied by itself once. This is written as \( x^2 \), where 2 is the exponent.
• Mathematical Expression: Squaring a number \( x \) can be expressed as:

  
  \[
  x^2 = x \times x
  \]

• Example Calculation: To square the number 4, you perform the following calculation:

  
  \[
  4^2 = 4 \times 4 = 16
  \]

• Properties of Squaring:
  • Squaring a positive number results in a positive number.
  • Squaring a negative number results in a positive number (since multiplying two negative numbers yields a positive product).
  • Squaring zero results in zero.

Squaring numbers is a key operation in many mathematical concepts, including polynomial equations, geometry (such as finding the area of squares), and calculus. Understanding the process and properties of squaring helps in grasping more complex mathematical theories and applications.

Calculating 4 squared involves a simple process of multiplying the number 4 by itself. This operation is fundamental in arithmetic and is often used in various mathematical applications. Here is a detailed, step-by-step explanation:

1. Identify the Base Number:

   The base number to be squared is 4.

2. Understand the Exponent:

   The exponent is 2, indicating that the base number is multiplied by itself. This is written as \( 4^2 \).

3. Write the Multiplication Expression:

   Express the operation as a multiplication:

   
   \[
   4^2 = 4 \times 4
   \]

4. Perform the Multiplication:

   Multiply the base number by itself:

   
   \[
   4 \times 4 = 16
   \]

5. Result:

   The result of squaring 4 is 16.

Therefore, \( 4^2 = 16 \). This means that when you multiply 4 by itself, the product is 16. Squaring numbers is a basic yet essential operation in mathematics, and understanding how to perform it accurately is crucial for more advanced mathematical concepts and applications.

Squaring numbers is a fundamental mathematical operation with a wide range of applications in various fields. Understanding how to square numbers and their practical uses can enhance problem-solving skills and mathematical comprehension. Here are some detailed applications of squaring numbers:

• Geometry:

  In geometry, squaring is used to calculate the area of a square. If the side length of a square is \( s \), the area is given by \( s^2 \). For example, if a square has a side length of 4 units, its area is:

  
  \[
  \text{Area} = 4^2 = 16 \text{ square units}
  \]

• Algebra:

  Squaring is essential in algebra, particularly in solving quadratic equations of the form \( ax^2 + bx + c = 0 \). The solutions to these equations often involve squaring numbers and manipulating squared terms.

• Physics:

  In physics, squaring is used in various formulas. For example, the kinetic energy (\( KE \)) of an object is calculated using the formula:

  
  \[
  KE = \frac{1}{2} mv^2
  \]

  where \( m \) is the mass of the object and \( v \) is its velocity. Here, the velocity is squared to determine the kinetic energy.

• Statistics:

  In statistics, squaring is used to calculate the variance and standard deviation, which are measures of data dispersion. The variance is the average of the squared differences from the mean, and it is given by:

  
  \[
  \text{Variance} = \frac{\sum (x_i - \mu)^2}{N}
  \]

  where \( x_i \) represents each data point, \( \mu \) is the mean, and \( N \) is the number of data points.

• Engineering:

  In engineering, squaring is used in various calculations, such as determining the moment of inertia, which is crucial for analyzing the rotational motion of objects. The moment of inertia for a rotating object is given by:

  
  \[
  I = \sum m_i r_i^2
  \]

  where \( m_i \) is the mass of each particle and \( r_i \) is the distance from the axis of rotation.

Overall, the operation of squaring numbers is a versatile tool in mathematics and science, enabling the solution of complex problems and the understanding of various phenomena.

Squared numbers, also known as perfect squares, have several unique and interesting properties. Understanding these properties is crucial for grasping more advanced mathematical concepts and solving various types of problems. Here are some key properties of squared numbers:

• Non-Negativity:

  When any real number is squared, the result is always non-negative. This is because the product of two positive numbers is positive, and the product of two negative numbers is also positive. For example:

  
  \[
  4^2 = 16 \quad \text{and} \quad (-4)^2 = 16
  \]

• Even and Odd Squares:

  The square of an even number is always even, and the square of an odd number is always odd. For instance:
  

  
  
  • 
    \[
    2^2 = 4 \quad \text{(even number)}
    \]
    
  
  
  • 
    \[
    3^2 = 9 \quad \text{(odd number)}
    \]
    
  
  
  
  


• Growth Rate:

  Squared numbers grow rapidly. As the base number increases, the squared value increases much more quickly. For example:

  
  \[
  2^2 = 4, \quad 3^2 = 9, \quad 4^2 = 16, \quad 5^2 = 25
  \]

• Sum of Consecutive Odd Numbers:

  The square of a number is equal to the sum of the first \( n \) consecutive odd numbers. For example, for \( n = 4 \):

  
  \[
  4^2 = 1 + 3 + 5 + 7 = 16
  \]

• Geometric Interpretation:

  The square of a number represents the area of a square with side lengths equal to that number. For example, a square with a side length of 4 units has an area of:

  
  \[
  4^2 = 16 \text{ square units}
  \]

• Distance Formula:

  In coordinate geometry, the square of the differences in coordinates is used in the distance formula to find the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\):

  
  \[
  \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
  \]

These properties illustrate the significance of squared numbers in various mathematical contexts, from basic arithmetic to advanced geometry and algebra. Understanding these properties is essential for solving complex mathematical problems and for applications in science and engineering.

Squaring numbers is a fundamental mathematical operation with numerous practical applications in everyday life. Here are some detailed examples of how squaring is used in real-world scenarios:

• Calculating Area:

  In geometry, squaring is commonly used to calculate the area of square-shaped spaces. If you have a square garden with each side measuring 4 meters, the area is:

  
  \[
  \text{Area} = 4^2 = 16 \text{ square meters}
  \]

• Physics - Kinetic Energy:

  In physics, the kinetic energy (KE) of a moving object is determined by squaring its velocity. The formula for kinetic energy is:

  
  \[
  KE = \frac{1}{2} mv^2
  \]

  where \( m \) is the mass and \( v \) is the velocity. For example, if an object with a mass of 2 kg is moving at a velocity of 4 m/s, its kinetic energy is:

  
  \[
  KE = \frac{1}{2} \times 2 \times 4^2 = \frac{1}{2} \times 2 \times 16 = 16 \text{ joules}
  \]

• Finance - Compound Interest:

  In finance, squaring is used to calculate compound interest, where the interest earned over time is squared. For example, the formula for compound interest is:

  
  \[
  A = P \left(1 + \frac{r}{n}\right)^{nt}
  \]

  If the interest is compounded annually, and you want to calculate the amount after 2 years (where the exponent is 2), the calculation involves squaring.

• Construction - Load Bearing:

  In construction, squaring is used to determine the load-bearing capacity of beams and columns. The moment of inertia, which is crucial for structural stability, involves squaring the dimensions of the cross-section. For example, the moment of inertia for a rectangular beam is:

  
  \[
  I = \frac{b h^3}{12}
  \]

  where \( b \) is the base width and \( h \) is the height. If \( h = 4 \) meters, then \( h^3 = 4^3 = 64 \) cubic meters.

• Technology - Digital Imaging:

  In digital imaging, the resolution of an image is often expressed in terms of megapixels, which involves squaring the pixel dimensions. For example, an image with 4,000 pixels by 3,000 pixels has a resolution of:

  
  \[
  4,000 \times 3,000 = 12,000,000 \text{ pixels or 12 megapixels}
  \]

These examples illustrate how the concept of squaring numbers is applied in various fields, highlighting its practical significance and utility in solving real-life problems.

Squaring numbers plays a crucial role in geometry, with numerous applications and significant implications. Below are some key points highlighting the importance of squaring in various geometric contexts:

• Area Calculation: The concept of squaring is directly tied to the calculation of the area of squares and other geometric shapes. For instance, the area of a square is calculated as the square of its side length (\(A = s^2\)). This principle extends to other shapes, such as the area of a circle being proportional to the square of its radius (\(A = \pi r^2\)).
• Pythagorean Theorem: One of the most well-known applications of squaring in geometry is the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse (\(c^2\)) is equal to the sum of the squares of the other two sides (\(a^2 + b^2\)). This theorem is fundamental in many geometric proofs and calculations.
• Distance Formula: In coordinate geometry, the distance between two points is derived using the square of the differences in their coordinates. The distance formula \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\) relies on squaring the differences to ensure non-negative values before summing and taking the square root.
• Surface Area and Volume: In three-dimensional geometry, the surface area of objects like cubes and spheres involves squaring. For example, the surface area of a sphere is given by \(4\pi r^2\), and the volume of a cube is the cube of its side length, which involves squaring as an intermediate step (\(V = s^3 = s \cdot s^2\)).
• Inverse-Square Law: In physical geometry and physics, the inverse-square law describes how certain physical quantities diminish with the square of the distance from a source. For instance, gravitational and electromagnetic forces follow this law, indicating the fundamental relationship between squaring and spatial dimensions.
• Quadratic Forms: In linear algebra and higher-dimensional geometry, quadratic forms, which are expressions involving squared terms, are used to describe various properties and transformations of geometric shapes and spaces. These forms are essential in understanding the geometry of conic sections, optimization problems, and more.

Overall, the act of squaring numbers is not just a mathematical operation but a fundamental tool in geometric reasoning and problem-solving, impacting various areas from basic shape properties to advanced theoretical constructs.

Squaring numbers is a fundamental operation in algebra with wide-ranging applications. Here are some key areas where squaring is crucial:

• Solving Quadratic Equations: Quadratic equations, which are polynomials of degree two, often involve squared terms. The general form of a quadratic equation is \(ax^2 + bx + c = 0\). To solve these, we can use the quadratic formula:

  \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

  This formula is derived from completing the square, showcasing the importance of understanding squaring in solving such equations.

• Distance Formula: The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in the Cartesian plane is given by the distance formula, which is derived from the Pythagorean theorem:

  \[d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]

  Here, squaring the differences between the coordinates is essential to compute the Euclidean distance.

• Exponentiation and Growth: Squaring is a specific case of exponentiation where the exponent is 2. It models various growth processes such as area growth (e.g., a square's area is side length squared) and certain financial calculations.

• Algebraic Identities: Many algebraic identities involve squaring, such as the difference of squares and the square of a binomial:

  \[(a + b)^2 = a^2 + 2ab + b^2\]

  \[(a - b)^2 = a^2 - 2ab + b^2\]

  These identities simplify complex expressions and are used extensively in algebraic manipulations.

• Variance and Standard Deviation: In statistics, variance is the average of the squared differences from the mean, and standard deviation is the square root of variance:

  \[\sigma^2 = \frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2\]

  Squaring the deviations ensures that negative differences do not cancel out positive ones, providing a measure of data dispersion.

• Optimization Problems: Squaring functions are used in optimization to minimize or maximize certain quantities. For example, the method of least squares involves minimizing the sum of the squares of the differences between observed and predicted values.

Overall, squaring is an indispensable operation in algebra, providing foundational tools for solving equations, analyzing data, and modeling various phenomena.

Squaring is a fundamental mathematical operation that finds extensive applications in physical science. It is crucial in describing and understanding various physical phenomena. Here are some key areas where squaring is particularly important:

• Kinetic Energy:

  The kinetic energy (\(E_k\)) of an object is given by the formula:

  \[ E_k = \frac{1}{2}mv^2 \]
  where \(m\) is the mass of the object and \(v\) is its velocity. The velocity is squared in this formula, highlighting how an increase in velocity leads to a significantly larger increase in kinetic energy. This quadratic relationship explains why high-speed collisions result in much greater energy release compared to low-speed impacts.

• Gravitational Potential Energy:

  In gravitational physics, the potential energy (\(U\)) between two masses is often described using a squared term in the denominator:

  \[ U = -\frac{Gm_1m_2}{r} \]
  where \(G\) is the gravitational constant, \(m_1\) and \(m_2\) are the masses, and \(r\) is the distance between them. Although the formula itself does not contain a squared term directly, the inverse square law applies to gravitational force (\(F = G\frac{m_1m_2}{r^2}\)), showing how gravitational force diminishes with the square of the distance.

• Electromagnetic Fields:

  In electromagnetism, the strength of electric and magnetic fields diminishes with the square of the distance from the source. For example, Coulomb's law for the electric force (\(F\)) between two charges is given by:

  \[ F = k_e \frac{q_1q_2}{r^2} \]
  where \(k_e\) is Coulomb's constant, \(q_1\) and \(q_2\) are the charges, and \(r\) is the distance between them. This inverse square law demonstrates how field strength decreases rapidly as distance increases, which is essential in understanding how electric and magnetic fields interact with matter.

• Wave Intensity:

  For waves, such as sound or light, the intensity (\(I\)) of the wave is proportional to the square of the amplitude (\(A\)):

  \[ I \propto A^2 \]
  This relationship shows that the energy carried by a wave increases significantly with amplitude, making squaring vital in the study of wave phenomena, including acoustics and optics.

• Dimensional Analysis:

  In physics, dimensional analysis often involves squaring quantities to ensure that equations remain dimensionally consistent. For instance, when velocity (\(v\)) is squared, its dimensions change from length/time (\(L/T\)) to length squared per time squared (\(L^2/T^2\)). This principle is critical in deriving and verifying physical formulas.

Overall, squaring is an indispensable tool in physical science, helping to describe and quantify the behavior of various physical systems accurately.

Understanding the process of squaring numbers is fundamental in mathematics, but several common mistakes and misconceptions can occur. These errors often stem from misunderstandings of basic principles or misapplication of rules.

• Misunderstanding the Squaring Process:

  One of the most common mistakes is the belief that squaring a binomial is the same as squaring its terms individually. For example, students often think that \((a + b)^2 = a^2 + b^2\), which is incorrect. The correct expansion is \((a + b)^2 = a^2 + 2ab + b^2\).

• Forgetting Negative Solutions:

  When solving equations involving squares, such as \(x^2 = 25\), it is important to remember that \(x\) can be both positive and negative. Thus, \(x = 5\) and \(x = -5\) are both solutions. Overlooking the negative solution is a frequent error.

• Incorrect Order of Operations:

  In some cases, students may incorrectly apply the order of operations. For example, when calculating \(-5^2\), the correct interpretation is \(-(5^2) = -25\), not \((-5)^2 = 25\).

• Misapplication of Exponents:

  Students often confuse the rules for exponents. For instance, they might incorrectly apply the product of powers rule, thinking that \(x^2 \cdot x^4 = x^8\), when it should be \(x^2 \cdot x^4 = x^{2+4} = x^6\).

• Square Roots Misconceptions:

  A common misconception is the belief that the square root of a sum can be simplified as the sum of the square roots, i.e., \(\sqrt{a + b} = \sqrt{a} + \sqrt{b}\), which is not true. The correct approach is to leave the expression as \(\sqrt{a + b}\) unless it can be simplified by factoring.

Recognizing and addressing these common mistakes and misconceptions is crucial for mastering algebraic concepts and ensuring a solid mathematical foundation.

In higher mathematics, the concept of squaring extends beyond basic arithmetic and finds applications in various advanced fields. Understanding these applications is crucial for delving deeper into mathematical theory and its practical uses. Here are some advanced topics where squaring plays a significant role:

• Quadratic Equations:

  Quadratic equations are polynomial equations of the form \(ax^2 + bx + c = 0\). Solving these equations involves squaring and can be done using the quadratic formula:

  \[
  x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a}
  \]

• Calculus - Derivatives and Integrals:

  In calculus, squaring functions is fundamental in finding derivatives and integrals. For instance, the power rule for differentiation states that if \(f(x) = x^n\), then \(f'(x) = nx^{n-1}\). This rule is often applied when \(n = 2\), such as finding the derivative of \(x^2\).

  \[
  \frac{d}{dx} x^2 = 2x
  \]

• Matrix Algebra:

  Squaring is also crucial in matrix algebra, especially when dealing with symmetric matrices and eigenvalues. If \(A\) is a matrix, then \(A^2 = A \cdot A\) and squaring the matrix can help in finding powers of matrices, which is useful in solving systems of linear equations.

• Complex Numbers:

  In the realm of complex numbers, squaring is used to explore properties and transformations. For a complex number \(z = a + bi\), its square is given by:

  \[
  z^2 = (a + bi)^2 = a^2 - b^2 + 2abi
  \]

• Number Theory:

  Squaring plays a significant role in number theory, particularly in the study of congruences and quadratic residues. For example, understanding which numbers are perfect squares modulo a given integer is a fundamental problem in this field.

• Geometric Applications:

  In geometry, squaring is used to calculate areas and distances. For instance, the area of a square with side length \(s\) is \(s^2\), and the distance formula in the Euclidean plane involves squaring the differences of coordinates.

  \[
  \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
  \]

These examples illustrate the importance of squaring in higher mathematics, providing tools and techniques that are essential for advanced study and application in various mathematical fields.

In this comprehensive guide, we have explored the concept of squaring numbers, specifically focusing on the example of 4 squared, which is \( 4^2 = 16 \). Squaring numbers is a fundamental mathematical operation with wide-ranging applications across various fields.

We began by understanding the mathematical definition of squaring and provided a step-by-step calculation of 4 squared. This foundational knowledge paved the way for exploring the numerous applications of squaring in geometry, algebra, physical sciences, and beyond.

Throughout the guide, we examined the properties of squared numbers, noting their role in forming perfect squares and their implications in solving quadratic equations. We also highlighted the importance of squaring in geometry, where it is used to calculate areas of squares and other shapes, and in algebraic expressions, where it aids in simplifying and solving equations.

Real-life examples illustrated the practical use of squaring, from computing areas to understanding exponential growth patterns. We also discussed common mistakes and misconceptions, such as confusing squaring with other mathematical operations, and provided strategies to avoid these errors.

In advanced mathematical contexts, squaring plays a crucial role in higher-level concepts such as complex numbers and calculus, demonstrating its significance beyond basic arithmetic.

In summary, understanding and applying the concept of squaring is essential for students, professionals, and anyone interested in mathematics. It provides a solid foundation for more complex mathematical operations and enhances problem-solving skills across various disciplines.

• Key points covered in this guide include:
• Mathematical definition and step-by-step calculation of 4 squared.
• Applications of squaring in geometry and algebra.
• Real-life examples and practical uses.
• Common mistakes and misconceptions.
• Advanced applications in higher mathematics.

By mastering the concept of squaring, one can gain deeper insights into mathematical principles and their real-world applications, paving the way for continued learning and exploration in the field of mathematics.