Topic u substitution with square roots: Explore the power of U substitution combined with square roots in mastering integration techniques. This comprehensive guide unveils the fundamentals of U substitution and delves into strategies for effectively integrating functions involving square roots. Dive into practical examples, tips, and common pitfalls to enhance your understanding and proficiency in handling complex integrals.
Table of Content
- U-Substitution with Square Roots
- Table of Contents
- 1. Introduction to U Substitution
- 2. Basics of Square Roots and Their Properties
- 3. Understanding the Integration Process
- 4. Applying U Substitution Technique
- 5. Examples of U Substitution with Square Roots
- 6. Strategies for Handling Complex Square Root Integrals
- 7. Tips and Tricks for Effective U Substitution
- 8. Common Mistakes to Avoid
- 9. Advanced Applications and Challenges
- 10. Conclusion and Recap
- YOUTUBE: Xem video để học cách tính tích phân với căn bậc hai bằng phép thay đổi biến u. Bài giảng chi tiết và dễ hiểu.
U-Substitution with Square Roots
U-substitution is a method used in calculus to simplify the process of finding integrals, especially when dealing with functions involving square roots. This technique is particularly useful for integrals where the integrand is a composite function, and the inner function's derivative is present.
Basic Steps for U-Substitution
- Choose u: Identify a function of x that, when differentiated, produces a part of the integrand.
- Differentiate u: Compute du and solve for dx.
- Substitute: Replace all instances of x with u and dx with du in the integral.
- Integrate: Perform the integration in terms of u.
- Back-substitute: Convert the result back in terms of x.
Example 1: Indefinite Integral
Consider the integral:
\(\int 6x(x^2 + 4)^4 \, dx\)
Let \(u = x^2 + 4\). Then \(du = 2x \, dx\) and \(dx = \frac{du}{2x}\). Adjusting for \(6x \, dx\), we get \(du = 6x \, dx\).
Rewriting the integral in terms of \(u\):
\(\int u^4 \, du\)
The antiderivative is:
\(\frac{u^5}{5} + C\)
Substitute back \(u = x^2 + 4\):
\(\frac{(x^2 + 4)^5}{5} + C\)
Example 2: Definite Integral
Consider the integral:
\(\int_{1}^{2} 2x(x^2 + 1)^3 \, dx\)
Let \(u = x^2 + 1\). Then \(du = 2x \, dx\) and we change the limits of integration accordingly:
- When \(x = 1\), \(u = 1^2 + 1 = 2\)
- When \(x = 2\), \(u = 2^2 + 1 = 5\)
The integral in terms of \(u\) is:
\(\int_{2}^{5} u^3 \, du\)
Integrating gives:
\(\left[ \frac{u^4}{4} \right]_{2}^{5}\)
Evaluating this, we get:
\(\frac{5^4}{4} - \frac{2^4}{4} = \frac{625}{4} - \frac{16}{4} = \frac{609}{4}\)
Advanced Techniques
For more complex integrals, advanced techniques may be required:
- Non-standard substitutions
- Partial fraction decomposition after substitution
- Multiple substitutions
By using u-substitution, integrals involving square roots and other complex expressions can be simplified significantly, making them easier to solve.
Summary Table
| Original Integral | Substitution \(u\) | New Integral | Back-Substitution |
|---|---|---|---|
| \(\int 6x(x^2 + 4)^4 \, dx\) | \(x^2 + 4\) | \(\int u^4 \, du\) | \(\frac{(x^2 + 4)^5}{5} + C\) |
| \(\int \sin(3x) \, dx\) | 3x | \(\int \sin(u) \, du\) | \(-\cos(3x) + C\) |
Conclusion
Through u-substitution, complex integrals can be broken down into simpler forms, facilitating easier computation and better understanding of integration techniques.

READ MORE:
Table of Contents
1. Introduction to U Substitution
2. Basics of Square Roots and Their Properties
3. Understanding the Integration Process
- 3.1. Direct Integration of Functions with Square Roots
- 3.2. Limitations and Challenges
4. Applying U Substitution Technique
- 4.1. Identifying the Suitable U
- 4.2. Implementing U Substitution
5. Examples of U Substitution with Square Roots
- 5.1. Simple Examples
- 5.2. Complex Examples
6. Strategies for Handling Complex Square Root Integrals
- 6.1. Completing the Square
- 6.2. Rationalizing the Denominator
7. Tips and Tricks for Effective U Substitution
- 7.1. Choosing the Right U
- 7.2. Simplifying the Integral
8. Common Mistakes to Avoid
- 8.1. Misidentification of U
- 8.2. Incorrect Implementation
9. Advanced Applications and Challenges
- 9.1. Trigonometric Substitution
- 9.2. Substitution with Multiple Variables
10. Conclusion and Recap
1. Introduction to U Substitution
U substitution is a powerful technique used in calculus to simplify integrals by substituting a complex expression with a simpler variable. In this section, we'll explore the basics of U substitution and its significance in solving integrals involving square roots.
1.1. Understanding the Motivation Behind U Substitution
1.2. Key Concepts and Terminologies
- 1.2.1. The Chain Rule
- 1.2.2. Inverse Functions
1.3. Advantages of U Substitution
- 1.3.1. Simplifying Integrals
- 1.3.2. Handling Complex Functions
1.4. Application Scenarios
- 1.4.1. Integration of Trigonometric Functions
- 1.4.2. Integration of Exponential Functions
1.5. Limitations and Precautions
- 1.5.1. Restrictions on Substitution
- 1.5.2. Pitfalls to Avoid
2. Basics of Square Roots and Their Properties
In this section, we'll delve into the fundamental concepts of square roots and explore their properties that are crucial for understanding integration techniques involving square roots.
2.1. Definition and Notation of Square Roots
- 2.1.1. Understanding the Square Root Symbol
- 2.1.2. Basic Properties of Square Roots
2.2. Arithmetic Operations with Square Roots
- 2.2.1. Addition and Subtraction
- 2.2.2. Multiplication and Division
2.3. Properties of Square Roots in Integration
- 2.3.1. Behavior under Differentiation
- 2.3.2. Simplification Techniques
2.4. Common Patterns and Identities
- 2.4.1. Pythagorean Theorem
- 2.4.2. Quadratic Equations
2.5. Practical Examples and Applications
- 2.5.1. Real-life Scenarios
- 2.5.2. Engineering and Physics Applications
3. Understanding the Integration Process
Gain insight into the integration process and its significance in calculus, particularly when dealing with functions involving square roots. This section provides a comprehensive overview of the steps involved in integrating such functions.
3.1. Direct Integration of Functions with Square Roots
- 3.1.1. Identifying Integrals Requiring U Substitution
- 3.1.2. Applying Basic Integration Techniques
3.2. Limitations and Challenges
- 3.2.1. Complex Functions and Their Integrals
- 3.2.2. Strategies for Overcoming Integration Challenges

4. Applying U Substitution Technique
Explore the practical application of the U substitution technique in simplifying integrals involving square roots. This section provides a step-by-step guide on how to effectively implement U substitution to solve complex integration problems.
4.1. Identifying the Suitable U
- 4.1.1. Selecting a Suitable Variable for Substitution
- 4.1.2. Considering the Complexity of the Integral
4.2. Implementing U Substitution
- 4.2.1. Substituting U into the Integral
- 4.2.2. Simplifying the Integral with the New Variable
5. Examples of U Substitution with Square Roots
Illustrate the application of U substitution with square roots through various examples. This section provides a collection of example problems along with their solutions to demonstrate the effectiveness of the U substitution technique in solving integrals.
5.1. Simple Examples
- 5.1.1. Basic Integrals with Square Roots
- 5.1.2. Integrating Polynomials with Square Roots
5.2. Complex Examples
- 5.2.1. Trigonometric Functions with Square Roots
- 5.2.2. Exponential Functions with Square Roots
6. Strategies for Handling Complex Square Root Integrals
Handling integrals involving complex square roots can be challenging, but the use of u-substitution simplifies the process significantly. Here are detailed strategies to tackle such integrals:
- Identify a Suitable Substitution
Look for a substitution \( u \) that simplifies the integral. Typically, this means selecting \( u \) as an expression inside the square root or a related function. For example, for an integral involving \( \sqrt{x^2 + a^2} \), a good choice might be \( u = x^2 + a^2 \).
- Compute the Differential \( du \)
After choosing \( u \), compute \( du \). This step involves differentiating \( u \) with respect to \( x \). For instance, if \( u = x^2 + a^2 \), then \( du = 2x \, dx \).
- Substitute and Simplify
Replace the original variables and differentials in the integral with \( u \) and \( du \). This often turns the integral into a simpler form. Continuing the previous example, \( \int \sqrt{x^2 + a^2} \, dx \) becomes \( \int \sqrt{u} \frac{du}{2x} \).
- Integrate with Respect to \( u \)
Perform the integration in terms of \( u \). For the simplified integral, use standard integration techniques. For example, \( \int \sqrt{u} \, du \) becomes \( \frac{2}{3} u^{3/2} \).
- Back-Substitute to Original Variable
Finally, replace \( u \) with the original expression in terms of \( x \). This reverts the integral back to the original variable, completing the process. In our example, substituting back gives \( \frac{2}{3} (x^2 + a^2)^{3/2} \).
Examples
Here are some examples to illustrate these steps:
- Example 1: Integrating \( \sqrt{x^2 + a^2} \)
- Choose \( u = x^2 + a^2 \)
- Compute \( du = 2x \, dx \)
- Substitute: \( \int \sqrt{x^2 + a^2} \, dx = \int \sqrt{u} \frac{du}{2x} \)
- Simplify and integrate: \( \frac{1}{2} \int u^{1/2} \, du = \frac{1}{2} \cdot \frac{2}{3} u^{3/2} = \frac{1}{3} u^{3/2} \)
- Back-substitute: \( \frac{1}{3} (x^2 + a^2)^{3/2} \)
- Example 2: Integrating \( \frac{1}{\sqrt{x^2 - a^2}} \)
- Choose \( u = x^2 - a^2 \)
- Compute \( du = 2x \, dx \)
- Substitute: \( \int \frac{1}{\sqrt{x^2 - a^2}} \, dx = \int \frac{1}{\sqrt{u}} \frac{du}{2x} \)
- Simplify and integrate: \( \frac{1}{2} \int u^{-1/2} \, du = \frac{1}{2} \cdot 2u^{1/2} = u^{1/2} \)
- Back-substitute: \( \sqrt{x^2 - a^2} \)
By following these steps, you can effectively manage complex square root integrals using u-substitution. With practice, recognizing suitable substitutions and simplifying the integrals will become more intuitive.
7. Tips and Tricks for Effective U Substitution
U-substitution is a powerful technique for simplifying integrals, especially those involving square roots. Here are some tips and tricks to effectively use this method:
- Identify the Part to Substitute: Look for a part of the integral whose derivative appears elsewhere in the integrand. This often simplifies the integral significantly.
- Choose U Wisely: Select \( u \) such that the integral becomes simpler when substituted. For example, in integrals involving square roots like \( \sqrt{a^2 - x^2} \), choosing \( u = a^2 - x^2 \) can simplify the problem.
- Compute \( du \): After choosing \( u \), compute \( du \). Remember to adjust \( dx \) accordingly. For instance, if \( u = x^2 \), then \( du = 2x \, dx \).
- Simplify Before Substituting: Simplify the integral algebraically if possible before applying u-substitution. This can make the substitution step more straightforward and the integral easier to solve.
- Adjust Constants: If \( du \) includes a constant factor, adjust the integral accordingly. For example, if \( du = 3x \, dx \), then \( dx = \frac{1}{3x} \, du \).
- Split the Integral: For complex integrals, consider splitting them into simpler parts. This can sometimes make it easier to identify a useful substitution.
- Check Your Work: After finding the antiderivative, remember to substitute back the original variable to express the final answer in terms of the original integral.
- Practice Different Scenarios: Practice with various types of integrals to get comfortable with the process. This includes integrals of the form \( \int \sqrt{x^2 + a^2} \, dx \), \( \int \sqrt{a^2 - x^2} \, dx \), and \( \int \frac{1}{\sqrt{x^2 - a^2}} \, dx \).
- Use Trigonometric Identities: For integrals involving trigonometric functions, use relevant identities to simplify the integral before applying u-substitution. For example, use \( \cos^2 x = 1 - \sin^2 x \) in integrals involving \( \cos^2 x \).
- Combine Techniques: Sometimes, combining u-substitution with other techniques like integration by parts can simplify the integral further.
By following these tips and practicing regularly, you can master the u-substitution technique and tackle complex integrals involving square roots with confidence.
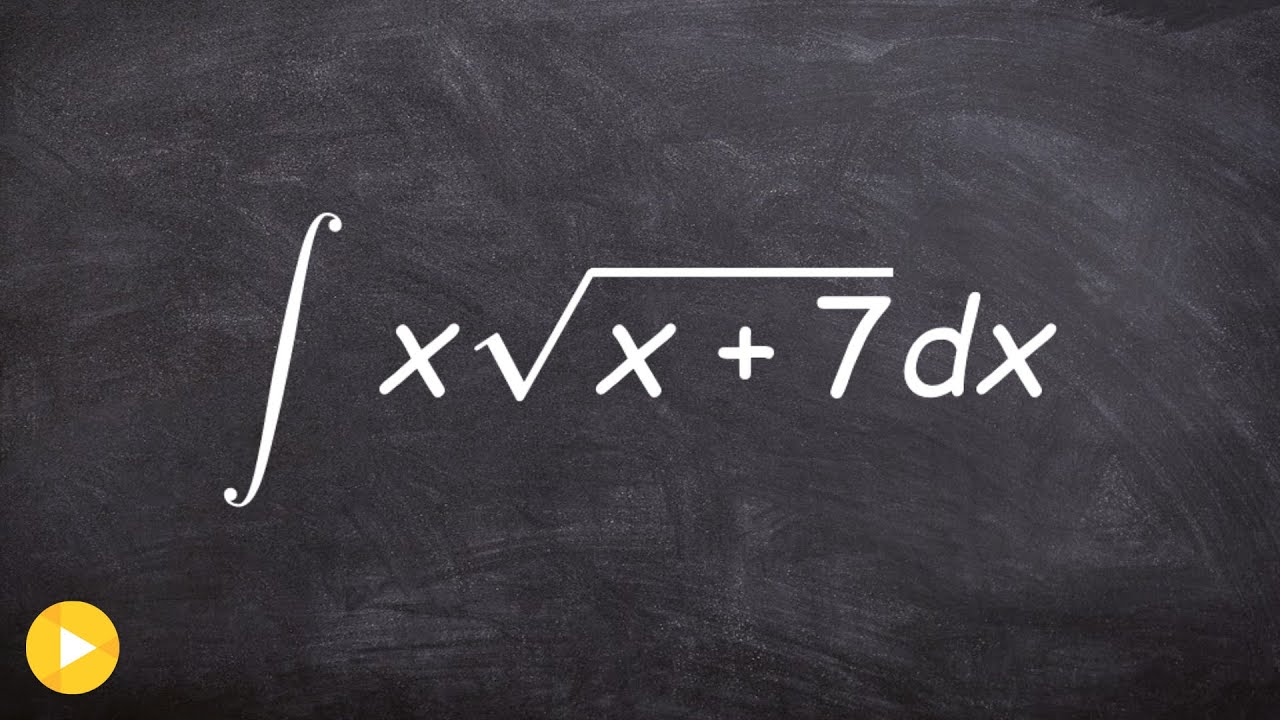
8. Common Mistakes to Avoid
When working with u substitution, particularly involving square roots, there are some common pitfalls that learners often encounter. Being aware of these mistakes can greatly improve your proficiency in solving such integrals. Here are some key points to keep in mind:
- Incorrect choice of u: One of the most frequent errors is selecting the wrong substitution variable, especially when dealing with square roots. Ensure that the chosen u simplifies the integral and leads to easier computation.
- Neglecting to adjust for du: After determining the substitution variable, it's crucial to compute its derivative du and adjust the integral accordingly. Failing to do so can result in incorrect solutions.
- Forgetting to change limits of integration: When substituting variables, don't overlook the need to change the limits of integration. Express the original limits in terms of the new variable to ensure accurate evaluation of the integral.
- Ignoring the constant of integration: Integrating with u substitution typically involves adding a constant of integration, denoted by +C. Neglecting to include this constant can lead to incomplete solutions.
- Incorrect application of algebraic manipulations: Sometimes, simplifying the integral after substitution requires careful algebraic manipulation, especially when dealing with square roots. Be diligent in your algebraic steps to avoid errors.
- Missing the opportunity for simplification: Occasionally, u substitution offers opportunities to simplify complex expressions before integration. Look for such simplifications to streamline your calculations and improve efficiency.
By being mindful of these common mistakes and practicing diligently, you can enhance your proficiency in u substitution with square roots and tackle integration problems more effectively.
9. Advanced Applications and Challenges
Exploring advanced applications and overcoming challenges in u substitution with square roots can deepen your understanding of integral calculus. Let's delve into some advanced topics and potential hurdles:
- Trigonometric substitutions: In more complex integrals involving square roots, trigonometric substitutions can offer alternative approaches to simplifying expressions. Understanding when and how to apply trigonometric substitutions can be a powerful tool in solving challenging integrals.
- Integration by parts: Combining u substitution with integration by parts can be necessary for handling integrals with square roots that resist straightforward methods. Mastering the interplay between these techniques can unlock solutions to a wide range of integrals.
- Parametric equations: Certain problems may benefit from converting integrals with square roots into parametric form. This approach can lead to elegant solutions by introducing new parameters and simplifying the integration process.
- Complex square roots: Integrals involving complex square roots present additional challenges due to the presence of imaginary numbers. Developing strategies to handle these complexities, such as employing complex conjugates or contour integration, is essential for tackling advanced problems.
- Numerical methods: When analytical methods fall short, numerical techniques like Simpson's rule or Monte Carlo integration can provide reliable approximations for integrals involving square roots. Familiarizing yourself with these methods expands your toolkit for solving challenging integration problems.
Despite the intricacies of advanced applications and challenges in u substitution with square roots, embracing these topics can sharpen your problem-solving skills and equip you with versatile approaches to integral calculus.
10. Conclusion and Recap
In conclusion, mastering u substitution with square roots opens up a world of possibilities in integral calculus. Let's recap the key points discussed throughout this comprehensive guide:
- Introduction to u substitution: Understanding the fundamental concept of u substitution and its importance in simplifying integrals.
- Basics of square roots and their properties: Familiarizing yourself with the properties of square roots lays the groundwork for applying u substitution effectively.
- Integration process: Gaining insight into the integration process and recognizing opportunities for u substitution to streamline calculations.
- Applying u substitution technique: Learning how to choose appropriate substitution variables and adjust integrals accordingly for successful integration.
- Examples of u substitution with square roots: Exploring practical examples illustrates the application of u substitution in solving integrals involving square roots.
- Strategies for handling complex square root integrals: Developing strategies for tackling complex integrals with square roots enhances problem-solving skills.
- Tips and tricks for effective u substitution: Incorporating tips and tricks streamlines the u substitution process and minimizes errors.
- Common mistakes to avoid: Being mindful of common mistakes helps avoid pitfalls and ensures accurate solutions.
- Advanced applications and challenges: Delving into advanced topics expands your toolkit for solving challenging integrals involving square roots.
By embracing these concepts and practicing regularly, you can become proficient in u substitution with square roots and approach integral calculus with confidence.
Xem video để học cách tính tích phân với căn bậc hai bằng phép thay đổi biến u. Bài giảng chi tiết và dễ hiểu.
Đánh giá tích phân với căn bậc hai sử dụng phép thay đổi biến
READ MORE:
Xem video để học cách tích phân sử dụng phép thay đổi biến u với căn bậc hai. Bài giảng chi tiết và dễ hiểu.
Tích phân sử dụng phép thay đổi biến với căn bậc hai








