Topic how to simplify with square roots: Learn how to simplify with square roots effortlessly with our comprehensive guide. This article breaks down the process into simple steps, making it easy for anyone to understand and apply. Discover techniques, examples, and tips to master the art of simplifying square roots efficiently.
Table of Content
- How to Simplify Square Roots
- Introduction
- Basic Concepts of Square Roots
- Methods to Simplify Square Roots
- Prime Factorization Method
- Examples of Simplifying Square Roots
- Simplifying Square Roots of Fractions
- Combining and Simplifying Multiple Square Roots
- Advanced Techniques for Simplifying Radicals
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- YOUTUBE: Hãy xem video này để học cách rút gọn căn bậc hai một cách dễ dàng và hiệu quả. Bạn sẽ tìm thấy các kỹ thuật và ví dụ cụ thể trong video này.
How to Simplify Square Roots
To simplify square roots, we use a variety of methods including prime factorization, the product rule, and the quotient rule. Here are the detailed steps and examples to guide you through the process.
Using the Prime Factorization Method
- Break the number inside the square root into its prime factors.
- For each pair of factors, take one factor out of the square root.
- Multiply the factors outside the square root and keep the remaining factors inside the square root.
Example:
√90
- Prime factorization: 90 = 2 × 3 × 3 × 5
- Take out pairs: 3
- Result: 3√10
Using the Product Rule
The product rule states that √ab = √a × √b.
Example:
Simplify √300
- Factor into perfect squares: 300 = 100 × 3
- Apply the product rule: √100 × √3 = 10√3
Using the Quotient Rule
The quotient rule states that √\frac{a}{b} = \frac{√a}{√b}.
Example:
Simplify √\frac{5}{36}
- Separate the numerator and denominator: \frac{√5}{√36}
- Simplify: \frac{√5}{6}
Examples of Simplifying Complex Expressions
Sometimes you need to simplify more complex expressions involving square roots. Here are some examples:
- Simplify: 2√12 + 9√3
- Solution: 2 × 2√3 + 9√3 = 4√3 + 9√3 = 13√3
- Simplify: √8
- Solution: √8 = √4 × 2 = √4 × √2 = 2√2
Fractions and Square Roots
To simplify a square root in the numerator or denominator of a fraction, use the quotient rule.
Example:
Simplify: \frac{√30}{√10}
- Combine the square roots: √\frac{30}{10} = √3
Practice Problems
Try simplifying these square roots on your own:
- Simplify: √50x^2y^3z
- Simplify: √12 × √3
- Simplify: √\frac{49}{81}
Use the methods described above to solve these problems.

READ MORE:
Introduction
Simplifying square roots is an essential skill in mathematics that involves reducing a square root to its simplest form. This process helps in making complex calculations easier and more manageable. The primary goal is to break down the number inside the square root into its prime factors and then apply the rules of square roots to simplify the expression. By following systematic steps, anyone can learn to simplify square roots accurately and efficiently. This guide will provide detailed methods, examples, and tips for mastering this fundamental mathematical technique.
Basic Concepts of Square Roots
Square roots are fundamental in mathematics, representing a value that, when multiplied by itself, gives the original number. The square root of a number \( n \) is denoted as \( \sqrt{n} \) and is the positive number that squares to \( n \). For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \). Here's a deeper look at the basic concepts:
- Radicand: The number under the square root symbol. In \( \sqrt{25} \), 25 is the radicand.
- Perfect Squares: Numbers whose square roots are integers. Examples include 1, 4, 9, 16, and 25.
- Non-Perfect Squares: Numbers that do not have integer square roots. For example, \( \sqrt{2} \) and \( \sqrt{3} \) are non-perfect squares.
- Product Rule: The square root of a product equals the product of the square roots. \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \).
- Quotient Rule: The square root of a quotient equals the quotient of the square roots. \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
Here are some examples to illustrate these concepts:
| Example | Steps | Result |
| \( \sqrt{12} \) |
|
\( 2\sqrt{3} \) |
| \( \sqrt{45} \) |
|
\( 3\sqrt{5} \) |
| \( \sqrt{18} \) |
|
\{ 3\sqrt{2} \) |
Understanding these basic concepts and rules allows for the simplification of square roots, making complex calculations more straightforward and manageable.
Methods to Simplify Square Roots
Simplifying square roots involves breaking down the radicand (the number inside the square root) into its prime factors and using various mathematical rules. Below are detailed methods to simplify square roots step by step:
-
Prime Factorization Method:
- Break the number in the square root into its prime factors.
- For each pair of identical factors, "take one out" of the square root sign.
- Multiply the remaining factors inside the square root sign.
- Example: To simplify \( \sqrt{90} \):
- Prime factors of 90: \( 90 = 2 \times 3 \times 3 \times 5 \)
- Take 3 out: \( \sqrt{90} = 3\sqrt{10} \)
-
Product Rule:
- Factor any perfect squares from the radicand.
- Write the radical expression as a product of simpler radical expressions.
- Simplify each radical expression.
- Example: To simplify \( \sqrt{12} \):
- Factor perfect square: \( 12 = 4 \times 3 \)
- Apply the product rule: \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3} \)
-
Quotient Rule:
- Write the radical expression as the quotient of two simpler radical expressions.
- Simplify the numerator and denominator separately.
- Example: To simplify \( \sqrt{\frac{5}{36}} \):
- Separate the fraction: \( \sqrt{\frac{5}{36}} = \frac{\sqrt{5}}{\sqrt{36}} \)
- Simplify: \( \frac{\sqrt{5}}{6} \)
Using these methods, you can simplify any square root expression to its simplest form, making complex calculations easier to manage.
Prime Factorization Method
The prime factorization method is a systematic way to simplify square roots by breaking down the number inside the square root into its prime factors. This method helps in identifying pairs of prime numbers which can be taken out of the square root for simplification.
- Find the Prime Factors:
Start by breaking the number into its prime factors. Prime factors are the prime numbers that multiply together to give the original number.
- Group the Factors:
Pair up identical prime factors. Each pair of prime factors can be taken out of the square root as a single number.
- Simplify:
Multiply the numbers taken out of the square root. The remaining numbers under the square root, if any, are multiplied together and stay inside the square root.
Here are a few examples to illustrate the method:
- Example 1: Simplify \(\sqrt{72}\)
- Prime factors of 72: \(72 = 2 \times 2 \times 2 \times 3 \times 3\)
- Pair the prime factors: \(2 \times 2\) and \(3 \times 3\)
- Simplify: \(2 \times 3 = 6\)
- Result: \(\sqrt{72} = 6\sqrt{2}\)
- Example 2: Simplify \(\sqrt{180}\)
- Prime factors of 180: \(180 = 2 \times 2 \times 3 \times 3 \times 5\)
- Pair the prime factors: \(2 \times 2\) and \(3 \times 3\)
- Simplify: \(2 \times 3 = 6\)
- Result: \(\sqrt{180} = 6\sqrt{5}\)
- Example 3: Simplify \(\sqrt{50}\)
- Prime factors of 50: \(50 = 2 \times 5 \times 5\)
- Pair the prime factors: \(5 \times 5\)
- Simplify: \(5\)
- Result: \(\sqrt{50} = 5\sqrt{2}\)
By following these steps, you can simplify any square root using the prime factorization method. This method is particularly useful for dealing with large numbers and ensuring accurate simplification.
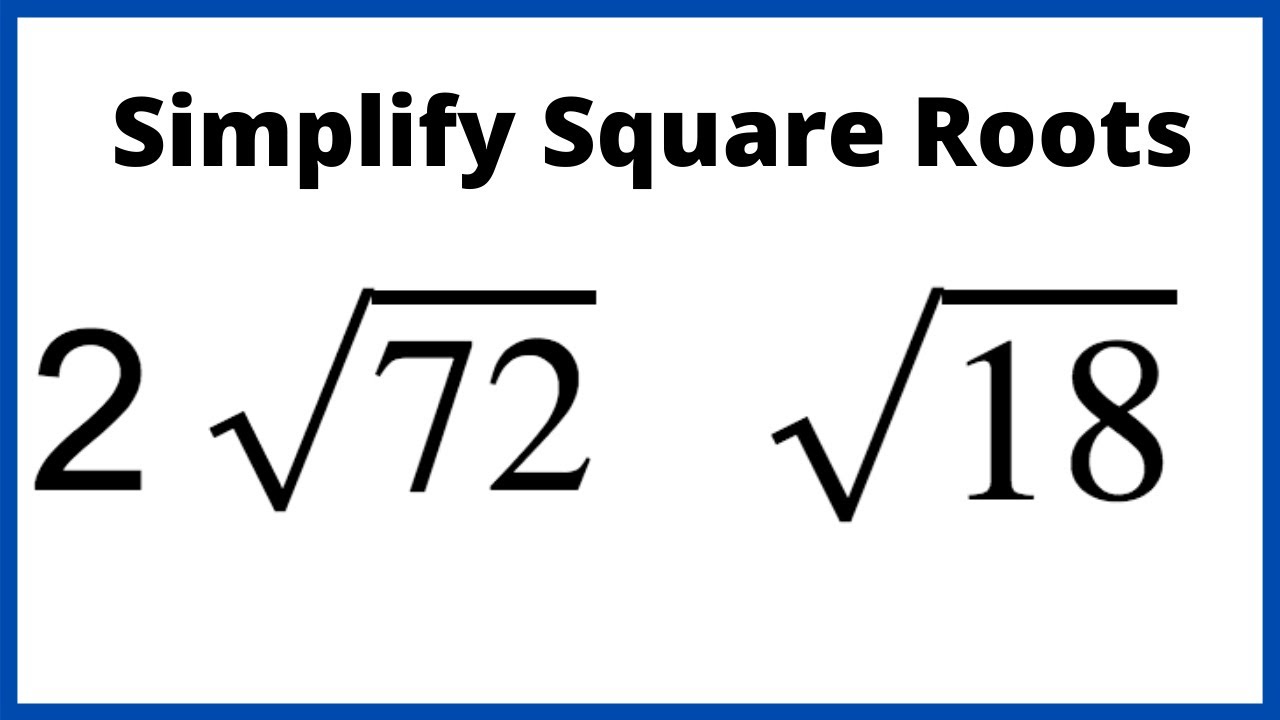
Examples of Simplifying Square Roots
Here are some detailed examples of how to simplify square roots step by step. Each example will demonstrate the process to help you understand the technique better.
Example 1: Simplify √12
- Factorize 12 into its prime factors: 12 = 2 × 2 × 3.
- Group the pairs of prime factors: 2 × 2 = 4.
- Take the square root of the grouped pair: √4 = 2.
- Combine with the remaining factor: 2√3.
- So, √12 simplifies to 2√3.
Example 2: Simplify √45
- Factorize 45 into its prime factors: 45 = 3 × 3 × 5.
- Group the pairs of prime factors: 3 × 3 = 9.
- Take the square root of the grouped pair: √9 = 3.
- Combine with the remaining factor: 3√5.
- So, √45 simplifies to 3√5.
Example 3: Simplify √72
- Factorize 72 into its prime factors: 72 = 2 × 2 × 2 × 3 × 3.
- Group the pairs of prime factors: 2 × 2 = 4 and 3 × 3 = 9.
- Take the square root of the grouped pairs: √4 = 2 and √9 = 3.
- Combine the results: 2 × 3 = 6.
- So, √72 simplifies to 6√2.
Example 4: Simplify √50
- Factorize 50 into its prime factors: 50 = 2 × 5 × 5.
- Group the pairs of prime factors: 5 × 5 = 25.
- Take the square root of the grouped pair: √25 = 5.
- Combine with the remaining factor: 5√2.
- So, √50 simplifies to 5√2.
Example 5: Simplify √32
- Factorize 32 into its prime factors: 32 = 2 × 2 × 2 × 2 × 2.
- Group the pairs of prime factors: 2 × 2 = 4 and 2 × 2 = 4.
- Take the square root of the grouped pairs: √4 = 2.
- Combine the results: 2 × 2 = 4.
- So, √32 simplifies to 4√2.
By following these examples and steps, you can simplify any square root expression. Practice with different numbers to become more proficient at this method.
Simplifying Square Roots of Fractions
To simplify square roots of fractions, follow these steps to achieve a simpler and more manageable form:
-
Simplify the Square Root:
Start by simplifying any square roots present in the fraction. For example, simplify √18/√9:
- √18 can be simplified as √(9×2) = 3√2
- √9 is 3, so the fraction becomes 3√2/3
The simplified form is √2.
-
Rationalize the Denominator:
If the square root is in the denominator, multiply both the numerator and the denominator by the square root found in the denominator to eliminate it. For example, simplify 1/√2:
- Multiply the numerator and the denominator by √2: (1×√2)/(√2×√2) = √2/2
The simplified form is √2/2.
Practice these methods with different fractions to become more comfortable with the process:
| Example | Simplified Form |
| √8/√2 | √4 = 2 |
| 3/√5 | (3√5)/5 |
| 2/√7 | (2√7)/7 |
By consistently applying these steps, simplifying square roots of fractions will become an easier and more intuitive process.
Combining and Simplifying Multiple Square Roots
Combining and simplifying multiple square roots involves grouping similar terms together and applying the rules of square roots to simplify the expression. Here are the steps to simplify expressions with multiple square roots:
- Group the Terms: Identify and group together terms with the same radicand (number under the square root symbol).
- Apply Basic Rules: Simplify each group separately by applying the basic rules of square roots, such as multiplying or dividing.
- Combine Like Terms: Combine the simplified terms by adding or subtracting them if they have the same radicand.
- Repeat if Necessary: If there are still multiple square roots remaining, repeat steps 1-3 until the expression is fully simplified.
Let's illustrate this with an example:
Simplify \( \sqrt{12} + 2\sqrt{27} - 3\sqrt{8} \).
1. Group the terms:
- Group 1: \( \sqrt{12} \)
- Group 2: \( 2\sqrt{27} \)
- Group 3: \( -3\sqrt{8} \)
2. Apply basic rules:
- Group 1: \( \sqrt{12} = \sqrt{4 \times 3} = 2\sqrt{3} \)
- Group 2: \( 2\sqrt{27} = 2\sqrt{9 \times 3} = 2 \times 3\sqrt{3} = 6\sqrt{3} \)
- Group 3: \( -3\sqrt{8} = -3\sqrt{4 \times 2} = -6\sqrt{2} \)
3. Combine like terms:
Combine the terms with the same radicand:
\( 2\sqrt{3} + 6\sqrt{3} - 6\sqrt{2} \)
Combine the coefficients:
\( (2 + 6)\sqrt{3} - 6\sqrt{2} = 8\sqrt{3} - 6\sqrt{2} \)
So, \( \sqrt{12} + 2\sqrt{27} - 3\sqrt{8} \) simplifies to \( 8\sqrt{3} - 6\sqrt{2} \).
Advanced Techniques for Simplifying Radicals
Advanced techniques for simplifying radicals involve strategies beyond basic methods like prime factorization. Here are some advanced techniques:
- Rationalizing Denominators: This technique involves multiplying the numerator and denominator of a fraction by an appropriate expression to eliminate radicals from the denominator.
- Conjugate Pairs: Using conjugate pairs is a technique to rationalize denominators. It involves multiplying the numerator and denominator of a fraction by the conjugate of the denominator to eliminate radicals.
- Completing the Square: In algebra, completing the square is a technique used to solve quadratic equations. It can also be used to simplify expressions involving radicals.
- Using Trigonometric Substitutions: In calculus, trigonometric substitutions are techniques used to simplify integrals involving radicals. These substitutions can also be applied to simplify radical expressions.
- Applying Advanced Algebraic Identities: Advanced algebraic identities like the difference of squares, sum or difference of cubes, etc., can sometimes be applied to simplify radical expressions.
Let's delve deeper into one of these techniques:
Rationalizing Denominators:
To rationalize the denominator of a fraction with a radical, multiply both the numerator and denominator by the conjugate of the denominator. This eliminates the radical from the denominator.
Example:
Rationalize the denominator of \( \frac{1}{\sqrt{3}} \).
Multiply both numerator and denominator by \( \sqrt{3} \) (the conjugate of \( \sqrt{3} \)):
\[
\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\]
So, \( \frac{1}{\sqrt{3}} \) simplifies to \( \frac{\sqrt{3}}{3} \).

Common Mistakes and How to Avoid Them
Understanding how to simplify square roots can be tricky, and there are common mistakes that students often make. Here are some of these mistakes and how to avoid them:
- Forgetting to Simplify: One common mistake is forgetting to simplify the radical expression fully. Always ensure that the expression is simplified as much as possible.
- Mistakes in Basic Arithmetic: Errors in basic arithmetic operations like addition, subtraction, multiplication, or division can lead to incorrect simplification. Double-check your calculations to avoid such mistakes.
- Confusion with Radicands: Sometimes, students confuse the radicand (the number under the square root symbol) with other parts of the expression. Pay close attention to the radicand when simplifying.
- Incorrect Application of Rules: Applying the rules of square roots incorrectly can result in errors. Make sure you understand the rules thoroughly and apply them accurately.
- Ignoring Negative Solutions: Square roots can have both positive and negative solutions, but sometimes students forget to consider the negative solution. Remember to consider both possibilities when simplifying.
Let's elaborate on one of these common mistakes:
Forgetting to Simplify:
It's important to fully simplify radical expressions to ensure accuracy in your calculations. Leaving expressions unsimplified can lead to incorrect answers. Always follow these steps:
- Prime Factorization: Decompose the radicand into its prime factors.
- Combine Like Terms: Combine the factors to simplify the expression.
Example:
Simplify \( \sqrt{36} + \sqrt{25} \).
1. Prime Factorization:
- \( \sqrt{36} = \sqrt{2^2 \times 3^2} = 2 \times 3 = 6 \)
- \( \sqrt{25} = \sqrt{5^2} = 5 \)
2. Combine Like Terms:
\( 6 + 5 = 11 \)
So, \( \sqrt{36} + \sqrt{25} \) simplifies to \( 11 \).
Practice Problems and Solutions
Practice problems are essential for mastering the skills of simplifying square roots. Here are some practice problems along with their solutions:
-
Problem: Simplify \( \sqrt{48} \).
Solution:
- Prime Factorization: \( \sqrt{48} = \sqrt{2^4 \times 3} = 4\sqrt{3} \)
-
Problem: Simplify \( \sqrt{75} + 2\sqrt{27} \).
Solution:
- Prime Factorization:
- \( \sqrt{75} = \sqrt{3 \times 5^2} = 5\sqrt{3} \)
- \( 2\sqrt{27} = 2 \times 3\sqrt{3} = 6\sqrt{3} \)
- Combine Like Terms: \( 5\sqrt{3} + 6\sqrt{3} = 11\sqrt{3} \)
- Prime Factorization:
-
Problem: Simplify \( \frac{\sqrt{15}}{\sqrt{5}} \).
Solution:
- Rationalize Denominator:
- Multiply numerator and denominator by \( \sqrt{5} \):
- \( \frac{\sqrt{15}}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{75}}{5} \)
- Prime Factorization: \( \sqrt{75} = 5\sqrt{3} \)
- Final Solution: \( \frac{5\sqrt{3}}{5} = \sqrt{3} \)
- Rationalize Denominator:
Hãy xem video này để học cách rút gọn căn bậc hai một cách dễ dàng và hiệu quả. Bạn sẽ tìm thấy các kỹ thuật và ví dụ cụ thể trong video này.
Cách Rút Gọn Căn Bậc Hai
READ MORE:
Xem video này để học cách rút gọn căn bậc hai với thầy J. Bạn sẽ tìm thấy các phương pháp và ví dụ thực tế trong video này.
Rút Gọn Căn Bậc Hai | Toán cùng thầy J









