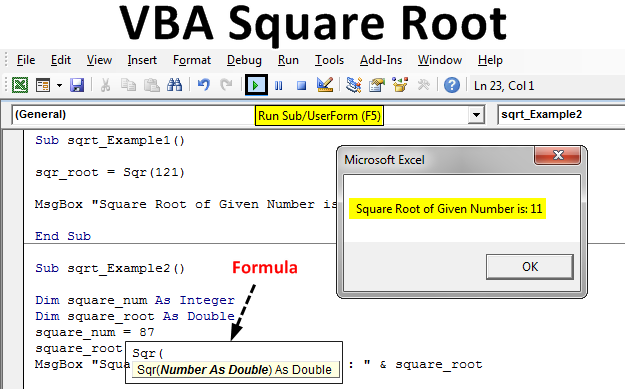
Topic square root worksheet pdf: Explore our collection of free square root worksheets in PDF format. Whether you're learning basic operations, simplifying square roots, or tackling advanced problems, these worksheets are designed to aid your understanding and practice. Download now to enhance your math skills and master the concepts of square roots effectively.
Table of Content
Square Root Worksheet PDF
Here is a curated list of resources for square root worksheets available in PDF format:
- - This worksheet covers basic to intermediate problems involving square roots.
- - Includes exercises on simplifying square roots and solving equations with square roots.
- - Advanced problems on square roots, including applications in geometry and algebra.
These worksheets are suitable for students learning about square roots and are available for free download.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, especially in algebra and geometry. Understanding square roots is crucial for solving equations, estimating quantities, and analyzing geometric shapes. Here's a step-by-step introduction:
- Definition: A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \).
- Basic Properties:
- Every positive number has two square roots: one positive and one negative.
- Zero has only one square root, which is zero itself.
- Negative numbers do not have real square roots, as the square of any real number is non-negative.
- Notation: The square root of \( x \) is denoted as \( \sqrt{x} \).
- Applications:
- Geometry: In geometry, square roots are used to find the lengths of sides of squares and other shapes.
- Physics and Engineering: They are essential in calculations involving forces, energies, and waveforms.
- Operations:
- Basic operations involving square roots include addition, subtraction, multiplication, and division.
- Techniques for simplifying square roots, such as factoring and rationalizing the denominator, are crucial skills.
Mastering square roots opens doors to advanced mathematical concepts and practical applications across various disciplines.
Basic Operations with Square Roots
Mastering the basic operations involving square roots is essential for tackling more complex mathematical problems. Here's a detailed guide on performing operations with square roots:
- Addition and Subtraction:
- To add or subtract square roots, ensure that the numbers under the square roots are the same. For example: \( \sqrt{9} + \sqrt{16} = 3 + 4 = 7 \).
- Multiplication:
- To multiply square roots, multiply the numbers under the roots. For example: \( \sqrt{9} \times \sqrt{16} = 3 \times 4 = 12 \).
- General formula: \( \sqrt{a} \times \sqrt{b} = \sqrt{ab} \).
- Division:
- To divide square roots, divide the numbers under the roots. For example: \( \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2 \).
- General formula: \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \), where \( b \neq 0 \).
- Complex Operations:
- Operations involving addition, subtraction, multiplication, and division of square roots require careful simplification and application of algebraic rules.
Practice these operations regularly to build confidence and proficiency in working with square roots.
Simplifying Square Roots
Simplifying square roots involves reducing them to their simplest form, making calculations easier and more manageable. Here’s a comprehensive guide on how to simplify square roots:
- Factorization Method:
- Factor the number under the square root into its prime factors.
- Take out any pairs of identical factors, one from inside and one from outside the square root.
- Examples:
- Simplify \( \sqrt{75} \):
\( \sqrt{75} = \sqrt{25 \times 3} \) \( \sqrt{75} = \sqrt{25} \times \sqrt{3} \) \( \sqrt{75} = 5 \times \sqrt{3} \) - Simplify \( \sqrt{48} \):
\( \sqrt{48} = \sqrt{16 \times 3} \) \( \sqrt{48} = \sqrt{16} \times \sqrt{3} \) \( \sqrt{48} = 4 \times \sqrt{3} \)
- Simplify \( \sqrt{75} \):
- Rationalizing Denominators:
- For expressions like \( \frac{1}{\sqrt{2}} \), multiply numerator and denominator by \( \sqrt{2} \) to rationalize the denominator.
- Practice:
- Regular practice with simplifying square roots enhances your proficiency in handling complex mathematical expressions.
By mastering the art of simplifying square roots, you can streamline your calculations and deepen your understanding of mathematical concepts.
Estimating Square Roots
Estimating square roots is a valuable skill for quickly approximating the value of a square root without using a calculator. Here’s how you can effectively estimate square roots:
- Identify Perfect Squares:
- Know common perfect squares (like \( 1^2 = 1, 2^2 = 4, 3^2 = 9, \) etc.) to gauge proximity.
- Use Nearby Perfect Squares:
- For a number \( x \), find the nearest perfect squares \( a^2 \) and \( b^2 \) such that \( a^2 \leq x \leq b^2 \).
- Estimate \( \sqrt{x} \) as \( a + \frac{x - a^2}{2a} \) if \( x \) is close to \( a^2 \).
- Example Estimations:
- Estimate \( \sqrt{17} \):
Nearest perfect squares: \( 4^2 = 16 \) and \( 5^2 = 25 \). Since \( 17 \) is closer to \( 16 \), estimate \( \sqrt{17} \approx 4 + \frac{17 - 16}{2 \times 4} = 4.125 \). - Estimate \( \sqrt{50} \):
Nearest perfect squares: \( 7^2 = 49 \) and \( 8^2 = 64 \). Since \( 50 \) is closer to \( 49 \), estimate \( \sqrt{50} \approx 7 + \frac{50 - 49}{2 \times 7} = 7.071 \).
- Estimate \( \sqrt{17} \):
- Practice and Refinement:
- Regular practice in estimating square roots enhances accuracy and confidence in mathematical problem-solving.
By mastering the technique of estimating square roots, you can expedite calculations and improve your overall mathematical fluency.

Word Problems Involving Square Roots
Word problems involving square roots can be a great way to apply your understanding of square roots to real-world scenarios. Below are several examples, along with detailed solutions, to help you master these types of problems.
Example 1: Area of a Square
A square garden has an area of 144 square meters. What is the length of one side of the garden?
- Identify the formula for the area of a square: \( A = s^2 \)
- Set up the equation with the given area: \( 144 = s^2 \)
- Solve for \( s \) by taking the square root of both sides: \( s = \sqrt{144} \)
- Calculate the square root: \( s = 12 \)
The length of one side of the garden is 12 meters.
Example 2: Speed and Distance
A car travels a distance of 225 kilometers in 5 hours. What is the car's average speed in kilometers per hour?
- Identify the formula for speed: \( \text{Speed} = \frac{\text{Distance}}{\text{Time}} \)
- Set up the equation with the given distance and time: \( \text{Speed} = \frac{225}{5} \)
- Calculate the speed: \( \text{Speed} = 45 \) kilometers per hour
The car's average speed is 45 kilometers per hour.
Example 3: Diagonal of a Square
A square has a side length of 10 meters. What is the length of the diagonal?
- Use the Pythagorean theorem for a right triangle formed by two sides and the diagonal: \( d^2 = s^2 + s^2 \)
- Set up the equation with the given side length: \( d^2 = 10^2 + 10^2 \)
- Simplify the equation: \( d^2 = 100 + 100 \) or \( d^2 = 200 \)
- Solve for \( d \) by taking the square root of both sides: \( d = \sqrt{200} \)
- Simplify the square root: \( d = 10\sqrt{2} \)
The length of the diagonal is \( 10\sqrt{2} \) meters, approximately 14.14 meters.
Practice Problems
- A square playground has an area of 256 square meters. What is the length of one side of the playground?
- A right triangle has legs of 6 meters and 8 meters. What is the length of the hypotenuse?
- A car travels 400 kilometers in 8 hours. What is the car's average speed?
- A square has a diagonal length of 14 meters. What is the length of one side?
Solutions to Practice Problems
- \( \sqrt{256} = 16 \) meters
- \( \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \) meters
- \( \frac{400}{8} = 50 \) kilometers per hour
- \( \frac{14}{\sqrt{2}} = 7\sqrt{2} \) meters, approximately 9.9 meters
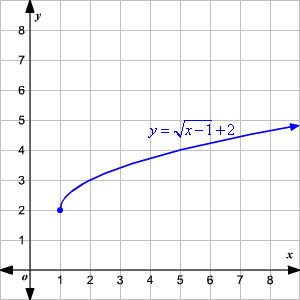
Graphing Square Root Functions
Graphing square root functions involves understanding the transformation of the basic square root graph \( y = \sqrt{x} \). Here's a step-by-step guide to help you grasp this concept:
- Identify the Function:
Consider a square root function of the form \( y = a\sqrt{b(x - h)} + k \). This represents the general form where:
- \( a \) affects the vertical stretch or compression and reflection.
- \( b \) affects the horizontal stretch or compression.
- \( h \) is the horizontal shift (left/right).
- \( k \) is the vertical shift (up/down).
- Plot the Basic Square Root Function:
Start with the parent function \( y = \sqrt{x} \). Create a table of values for \( x \) and \( y \):
x y = √x 0 0 1 1 4 2 9 3 - Apply Transformations:
Based on the values of \( a \), \( b \), \( h \), and \( k \), transform the basic graph accordingly:
- Vertical Stretch/Compression and Reflection (a): Multiply the \( y \)-values by \( a \). If \( a \) is negative, reflect the graph across the x-axis.
- Horizontal Stretch/Compression (b): Multiply the \( x \)-values by \( \frac{1}{b} \).
- Horizontal Shift (h): Add \( h \) to the \( x \)-values.
- Vertical Shift (k): Add \( k \) to the \( y \)-values.
- Draw the Graph:
Plot the transformed points on the coordinate plane and draw the curve of the square root function.
- Check the Domain and Range:
For the function \( y = \sqrt{x} \), the domain is \( x \geq 0 \) and the range is \( y \geq 0 \). After transformations:
- The domain becomes \( x \geq h \) if \( b \) is positive and \( x \leq h \) if \( b \) is negative.
- The range depends on \( a \) and \( k \). If \( a \) is positive, the range is \( y \geq k \); if \( a \) is negative, the range is \( y \leq k \).
By following these steps, you can graph any square root function accurately. Practice with different values of \( a \), \( b \), \( h \), and \( k \) to see how each parameter affects the graph.
Applications of Square Roots
Square roots have numerous applications in various fields. Below are some key areas where square roots are commonly used:
- Geometry: Square roots are essential in calculating the side length of a square when the area is known. For instance, if the area of a square is \(A\), the side length \(s\) can be found using \(s = \sqrt{A}\).
- Physics: In physics, square roots are often used in formulas involving distance, velocity, and acceleration. For example, the speed \(v\) of an object in free fall is calculated using \(v = \sqrt{2gh}\), where \(g\) is the acceleration due to gravity and \(h\) is the height.
- Statistics: The standard deviation, a measure of the amount of variation or dispersion of a set of values, is calculated using the square root of the variance.
- Finance: Square roots are used in various financial formulas, including the calculation of compound interest and the volatility of stock prices.
- Engineering: Engineers use square roots in structural analysis, electrical engineering, and signal processing to determine stress, resistance, and wave functions.
Here are some example problems involving square roots:
- Geometry Problem:
A square has an area of 49 square meters. What is the length of one side of the square?
Solution: \(s = \sqrt{49} = 7\) meters.
- Physics Problem:
An object is dropped from a height of 20 meters. Assuming no air resistance, what will be its speed just before it hits the ground? (Use \(g = 9.8 \, m/s^2\))
Solution: \(v = \sqrt{2 \cdot 9.8 \cdot 20} = \sqrt{392} \approx 19.8 \, m/s\).
- Finance Problem:
Calculate the volatility of a stock given a variance of 0.04.
Solution: Volatility \( \sigma = \sqrt{0.04} = 0.2\).
- Statistics Problem:
The variance of a data set is 16. What is the standard deviation?
Solution: Standard deviation \( \sigma = \sqrt{16} = 4\).
- Engineering Problem:
An electrical circuit has a resistance of 9 ohms and a current of 3 amperes. What is the power dissipated in the circuit?
Solution: Power \(P = I^2 \cdot R = 3^2 \cdot 9 = 81\) watts.
Challenges and Advanced Problems with Square Roots
Exploring advanced problems with square roots can deepen your understanding and enhance your mathematical skills. Here are some challenging concepts and exercises:
1. Complex Numbers and Square Roots
When dealing with square roots of negative numbers, we enter the realm of complex numbers. The imaginary unit \(i\) is defined as \(i = \sqrt{-1}\).
- Example: \(\sqrt{-16} = 4i\)
2. Rationalizing the Denominator
To rationalize the denominator means to eliminate any square roots in the denominator of a fraction. This is achieved by multiplying the numerator and the denominator by a suitable radical.
- Example: \(\frac{3}{\sqrt{2}} = \frac{3 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{3\sqrt{2}}{2}\)
3. Solving Equations Involving Square Roots
Equations that include square roots can often be solved by isolating the square root on one side and then squaring both sides of the equation.
- Example: Solve \(\sqrt{2x + 3} = 5\)
- Solution:
- Square both sides: \(2x + 3 = 25\)
- Simplify and solve for \(x\): \(2x = 22\), so \(x = 11\)
4. Square Roots and Exponents
Understanding the relationship between square roots and exponents is crucial for solving more complex problems.
- Example: \(x^{\frac{1}{2}} = \sqrt{x}\)
- Problem: Simplify \( \sqrt{x^4} \)
- Solution: \( \sqrt{x^4} = (x^4)^{\frac{1}{2}} = x^2 \)
5. Inequalities Involving Square Roots
Solving inequalities that involve square roots requires careful consideration of the domain of the function.
- Example: Solve \(\sqrt{x + 2} > 3\)
- Solution:
- Square both sides: \(x + 2 > 9\)
- Simplify and solve for \(x\): \(x > 7\)
Practice Problems
Here are some problems to practice your skills:
- Simplify: \( \sqrt{50} + \sqrt{18} \)
- Solve for \(x\): \( \sqrt{3x - 4} = 2 \)
- Rationalize the denominator: \( \frac{5}{\sqrt{3}} \)
- Simplify: \( \sqrt{a^2b^4} \)
- Solve the inequality: \( \sqrt{2x + 5} \leq 4 \)

Toán Học Vui - Số Mũ và Căn Bậc Hai
READ MORE:
Các Bài Tập Về Căn Bậc Hai