Topic square root of square root of 81: Welcome to our comprehensive guide on understanding the square root of the square root of 81. This article will take you through the fundamental concepts, various methods of calculation, and practical examples to help you grasp this intriguing mathematical concept with ease. Let's dive into the world of square roots together!
Table of Content
- Understanding the Square Root of the Square Root of 81
- Introduction to Square Roots
- Understanding the Square Root of 81
- Prime Factorization Method
- Repeated Subtraction Method
- Long Division Method
- Expressing the Square Root in Different Forms
- Calculating the Square Root of the Square Root of 81
- Examples and Practice Problems
- Applications of Square Roots in Real Life
- FAQs on Square Roots
- YOUTUBE:
Understanding the Square Root of the Square Root of 81
The concept of finding the square root of a square root can be understood through a step-by-step mathematical approach. Below, we explore the methods to find the value of the square root of the square root of 81.
Square Root of 81
The square root of 81 is a number that, when multiplied by itself, gives the product 81. This value is represented as √81.
Mathematically, √81 = 9, because 9 * 9 = 81.
Square Root of the Square Root of 81
To find the square root of the square root of 81, we need to take the square root of 9 (since √81 = 9).
Mathematically, this can be expressed as:
√(√81) = √9
Since the square root of 9 is 3 (because 3 * 3 = 9), we have:
√(√81) = 3
Methods to Calculate the Square Root
- Prime Factorization Method: Decompose 81 into its prime factors: 81 = 3 × 3 × 3 × 3. Therefore, √81 = √(3 × 3 × 3 × 3) = 3 × 3 = 9.
- Repeated Subtraction Method: Subtract successive odd numbers from 81 until you reach 0. The number of subtractions needed is the square root. For 81, it takes 9 subtractions (81 - 1 - 3 - 5 - 7 - 9 - 11 - 13 - 15 - 17 = 0), so √81 = 9.
- Long Division Method: Pair the digits of 81 from right to left and find a number whose square is less than or equal to 81. This number is 9, so √81 = 9.
Properties of the Square Root of 81
| Property | Value |
|---|---|
| Radical Form | √81 |
| Exponential Form | 81^(1/2) |
| Principal Square Root | +9 |
| Negative Square Root | -9 |
Example Problems
Example 1
Simplify √81 + 9:
Since √81 = 9, we have √81 + 9 = 9 + 9 = 18.
Example 2
Find the value of k if 2√81 + k = 28:
Given √81 = 9, we substitute and solve:
2(9) + k = 28 => 18 + k = 28 => k = 10.
Conclusion
The square root of the square root of 81 is a straightforward calculation once the concept of square roots is clear. The value is 3, and this can be confirmed through various mathematical methods. Understanding this concept helps build a strong foundation in algebra and number theory.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, particularly in algebra and geometry. A square root of a number is a value which, when multiplied by itself, gives the original number. Mathematically, for a given number \( x \), the square root is represented as \( \sqrt{x} \). For example, the square root of 81 is 9, since \( 9 \times 9 = 81 \).
There are several methods to determine the square root of a number, including prime factorization, repeated subtraction, and the long division method. Understanding these methods helps in solving various mathematical problems efficiently.
In this guide, we will explore these methods and their applications, along with detailed steps to calculate the square root of 81 and its significance.
Let’s begin by defining some key terms:
- Square Root: A number that, when multiplied by itself, equals the original number.
- Perfect Square: A number that has an integer as its square root.
- Radicand: The number under the radical sign.
- Principal Square Root: The non-negative square root of a number.
In the context of 81, it is important to note that it is a perfect square, and its principal square root is 9. This means 81 can be expressed as \( 9^2 \). Understanding these concepts is crucial for further exploration of square roots and their properties.
Understanding the Square Root of 81
The square root of a number is a value that, when multiplied by itself, gives the original number. For 81, the square root is 9, since \(9 \times 9 = 81\). This makes 81 a perfect square.
Here are different methods to understand and calculate the square root of 81:
- Prime Factorization Method:
- Express 81 as a product of prime factors: \(81 = 3 \times 3 \times 3 \times 3\)
- Group the prime factors in pairs: \(\sqrt{81} = \sqrt{(3 \times 3) \times (3 \times 3)} = 3 \times 3 = 9\)
- Repeated Subtraction Method:
- Subtract successive odd numbers from 81 until you reach 0.
- \(81 - 1 = 80\)
- \(80 - 3 = 77\)
- \(77 - 5 = 72\)
- Continue this process until: \(17 - 17 = 0\)
- The number of steps is 9, so \(\sqrt{81} = 9\).
- Long Division Method:
- Set up 81 in pairs of digits from the right.
- Find the largest number whose square is less than or equal to 81. This is 9.
- Use this number as the divisor and quotient, and perform the division to confirm \(9 \times 9 = 81\).
In summary, the square root of 81 is 9, which can be verified through various mathematical methods. The square root can be denoted as \(\sqrt{81} = 9\) or \(81^{1/2} = 9\).
Prime Factorization Method
The prime factorization method is a systematic approach to finding square roots by breaking down a number into its prime factors.
- Step 1: Find the prime factors of the number whose square root you want to calculate.
- Step 2: Pair up the prime factors in twos.
- Step 3: Take one factor from each pair and multiply them together.
- Step 4: The result of the multiplication is the square root of the original number.
This method is effective for integers and allows for the precise determination of square roots through clear steps of factorization and multiplication.
Repeated Subtraction Method
The repeated subtraction method is a straightforward approach to approximating the square root of a number through iterative subtraction.
- Step 1: Start with the number whose square root you want to find.
- Step 2: Subtract consecutive odd numbers (starting from 1) from the original number until the result is zero or a number close to zero.
- Step 3: Count the total number of subtractions performed. This count is the approximate square root of the original number.
This method is intuitive and doesn't require advanced mathematical operations, making it accessible for mental calculations and simple arithmetic.

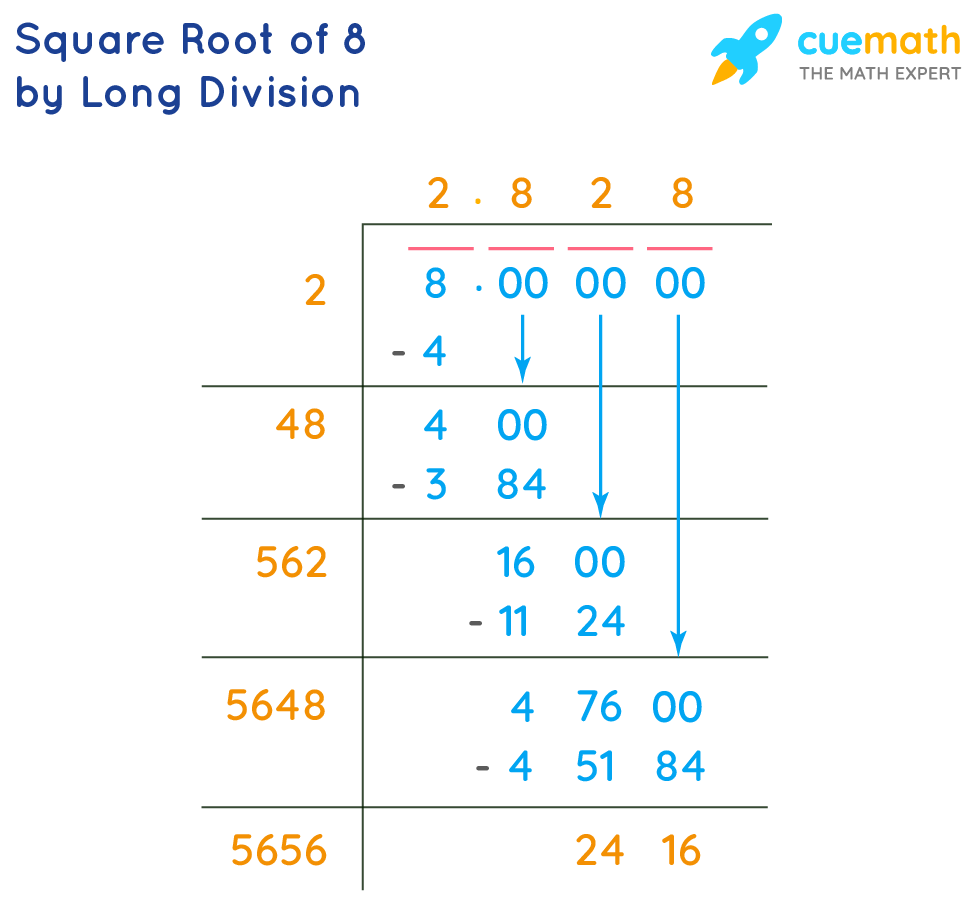
Long Division Method
The long division method is a step-by-step process to find the square root of a number. It is a systematic and reliable method for finding square roots, especially for large numbers. Below is the detailed procedure to find the square root of 81 using the long division method.
- Pair the Digits: Start by pairing the digits of the number from right to left. For 81, we have one pair: (81).
- Find the Largest Square: Find the largest number whose square is less than or equal to the first pair. In this case, the largest number is 9 because \( 9^2 = 81 \).
- Set up the Division: Write 9 as the divisor and the quotient. Place the quotient (9) above the pair (81).
- Multiply and Subtract: Multiply the divisor (9) by the quotient (9), which gives 81. Subtract this result from the pair (81 - 81 = 0).
- Continue the Process: Since there are no more digits to bring down and the remainder is 0, the process stops here.
- Result: The square root of 81 is 9.
Thus, the square root of 81 calculated using the long division method is 9. To find the square root of this result, we repeat the long division process for the number 9:
- Pair the Digits: The number 9 has only one digit, so we treat it as a single pair: (9).
- Find the Largest Square: The largest number whose square is less than or equal to 9 is 3 because \( 3^2 = 9 \).
- Set up the Division: Write 3 as the divisor and the quotient. Place the quotient (3) above the pair (9).
- Multiply and Subtract: Multiply the divisor (3) by the quotient (3), which gives 9. Subtract this result from the pair (9 - 9 = 0).
- Result: Since there are no more digits to bring down and the remainder is 0, the process stops here.
- Final Result: The square root of 9 is 3.
Therefore, the square root of the square root of 81 is 3. This process demonstrates the use of the long division method to find both the square root of 81 and its subsequent square root.
Expressing the Square Root in Different Forms
The square root of a number can be represented in various forms. Here, we will discuss the different ways to express the square root of 81.
- Radical Form: The most common way to represent the square root is using the radical symbol. For 81, it is expressed as:
\(\sqrt{81}\)
- Exponential Form: The square root can also be represented using exponents. The square root of 81 is expressed as:
\(81^{\frac{1}{2}}\)
- Positive and Negative Roots: Every positive number has two square roots: a positive and a negative root. For 81, the roots are:
\(\pm 9\)
This means both 9 and -9 are square roots of 81 since \(9^2 = 81\) and \((-9)^2 = 81\).
Step-by-Step Example
- Identify the number whose square root you want to find, in this case, 81.
- Express it in radical form:
\(\sqrt{81}\)
- Rewrite the radical expression in exponential form:
\(81^{\frac{1}{2}}\)
- Calculate the positive and negative roots:
\( \sqrt{81} = 9 \) and \( \sqrt{81} = -9 \)
Properties of the Square Root of 81
- Perfect Square: 81 is a perfect square, meaning it is the product of an integer multiplied by itself (9 * 9).
- Rational Number: The square root of 81 is a rational number since it can be expressed as a fraction (9/1 or -9/1).
- Principal Square Root: The positive root, 9, is known as the principal square root of 81.
Understanding these forms and properties helps in various mathematical calculations and problem-solving scenarios.
Calculating the Square Root of the Square Root of 81
To calculate the square root of the square root of 81, we first need to find the square root of 81 and then take the square root of that result. Here are the detailed steps:
Step 1: Finding the Square Root of 81
The square root of 81 can be calculated using the following methods:
- Prime Factorization Method: 81 can be expressed as \(3 \times 3 \times 3 \times 3\). Hence, the square root of 81 is \( \sqrt{81} = \sqrt{3^4} = 3^2 = 9 \).
- Long Division Method: Use the long division algorithm to find that \( \sqrt{81} = 9 \).
- Calculator: Input 81 into a calculator and press the square root button to get 9.
Therefore, the square root of 81 is 9.
Step 2: Finding the Square Root of 9
Now, we need to find the square root of 9:
- Prime Factorization Method: 9 can be expressed as \(3 \times 3\). Hence, the square root of 9 is \( \sqrt{9} = \sqrt{3^2} = 3 \).
- Long Division Method: Use the long division algorithm to find that \( \sqrt{9} = 3 \).
- Calculator: Input 9 into a calculator and press the square root button to get 3.
Therefore, the square root of 9 is 3.
Conclusion
The square root of the square root of 81 is:
\[
\sqrt{\sqrt{81}} = \sqrt{9} = 3
\]
Thus, the square root of the square root of 81 is 3.
Examples and Practice Problems
To help you understand and practice calculating the square root of the square root of 81, here are some detailed examples and practice problems.
Example 1: Basic Calculation
Let's start with the basic calculation:
- First, find the square root of 81. \[ \sqrt{81} = 9 \]
- Next, find the square root of the result. \[ \sqrt{9} = 3 \]
So, the square root of the square root of 81 is 3.
Example 2: Step-by-Step Verification
Let's verify this step by step:
- Calculate the square root of 81 using prime factorization: \[ 81 = 3 \times 3 \times 3 \times 3 = 3^4 \] Therefore, \[ \sqrt{81} = \sqrt{3^4} = 3^2 = 9 \]
- Then, calculate the square root of 9: \[ \sqrt{9} = 3 \]
Thus, our calculation is correct.
Practice Problems
- Find the square root of the square root of 49.
Solution: \[ \sqrt{49} = 7 \quad \text{and} \quad \sqrt{7} \] - Calculate the square root of the square root of 16.
Solution: \[ \sqrt{16} = 4 \quad \text{and} \quad \sqrt{4} = 2 \] - Determine the square root of the square root of 64.
Solution: \[ \sqrt{64} = 8 \quad \text{and} \quad \sqrt{8} \]
Additional Challenge Problems
Try solving these problems to test your understanding:
- Find the square root of the square root of 100.
Solution: \[ \sqrt{100} = 10 \quad \text{and} \quad \sqrt{10} \] - Calculate the square root of the square root of 144.
Solution: \[ \sqrt{144} = 12 \quad \text{and} \quad \sqrt{12} \] - Determine the square root of the square root of 256.
Solution: \[ \sqrt{256} = 16 \quad \text{and} \quad \sqrt{16} = 4 \]
Interactive Questions
For more practice, consider these interactive questions:
- What is the value of \(\sqrt{\sqrt{25}}\)?
- Simplify \(\sqrt{\sqrt{81 \times 16}}\).
- Calculate \(\sqrt{\sqrt{9 \times 49}}\).
These examples and problems should help reinforce your understanding of square roots and their properties. Keep practicing to improve your skills!

Applications of Square Roots in Real Life
Square roots play a significant role in various real-life applications across multiple fields. Understanding how square roots are applied can provide a deeper appreciation of their importance. Here are some notable applications:
- Finance: In finance, square roots are used to calculate stock market volatility and the rate of return on investments. For instance, the standard deviation, which is a measure of volatility, is the square root of the variance. This helps investors assess the risk of an investment.
- Architecture: Square roots are utilized to determine the natural frequency of structures like bridges and buildings. This helps engineers predict how these structures will respond to different loads, such as wind or traffic, ensuring safety and stability.
- Science: Many scientific calculations, including those for velocity, radiation absorption, and sound wave intensity, involve square roots. These calculations are crucial for developing new technologies and understanding natural phenomena.
- Statistics: In statistics, square roots are used to compute variance and standard deviation, which measure data dispersion. These metrics are essential for analyzing data sets and making informed decisions.
- Geometry: The Pythagorean theorem, which involves square roots, is used to calculate distances and solve problems involving right triangles. This is fundamental in fields like construction, carpentry, and navigation.
- Computer Science: Square roots are employed in various computer algorithms, including encryption, image processing, and game physics. For example, encryption algorithms use square roots to generate secure keys for data transmission.
- Navigation: Pilots and sailors use square roots to calculate distances between points on maps or globes. The Pythagorean theorem helps in determining the shortest path and course directions.
- Electrical Engineering: Square roots are used to compute power, voltage, and current in electrical circuits. These calculations are essential for designing and optimizing electrical systems.
- Cooking: In scaling recipes, square roots help maintain the correct proportions of ingredients. For example, if you double a recipe, using the square root of the scaling factor ensures the right balance of flavors.
- Photography: The f-number of a camera lens, which controls the amount of light entering the camera, involves square roots. Adjusting the f-number changes the exposure, crucial for capturing well-lit photographs.
Overall, the applications of square roots are vast and varied, spanning from everyday activities to complex scientific research. Understanding these applications can enhance problem-solving skills and promote the practical use of mathematical concepts in real life.
FAQs on Square Roots
Here are some frequently asked questions about square roots along with detailed answers to help you understand the concept better.
-
What is a square root?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 81 is 9, because \(9 \times 9 = 81\).
-
How do you represent a square root?
The square root is represented by the radical symbol (√). For instance, the square root of 81 is written as \(\sqrt{81}\).
-
Can square roots be negative?
Yes, a number can have both a positive and a negative square root. For example, the square roots of 25 are 5 and -5 because both \(5 \times 5\) and \(-5 \times -5\) equal 25. However, by convention, the symbol √ refers to the positive square root.
-
What are perfect squares?
Perfect squares are numbers that are the square of an integer. Examples include 1, 4, 9, 16, 25, etc. For instance, 81 is a perfect square because it equals \(9^2\).
-
How do you find the square root of a non-perfect square?
Finding the square root of a non-perfect square usually involves approximation methods or a calculator. For example, to find \(\sqrt{10}\), you know it is between 3 and 4 because \(3^2 = 9\) and \(4^2 = 16\). Using a calculator, you can find that \(\sqrt{10} \approx 3.162\).
-
Why is the square root of 81 written as ±9?
The square root of 81 is 9 because \(9 \times 9 = 81\). However, -9 is also a square root of 81 because \(-9 \times -9 = 81\). Therefore, \(\sqrt{81}\) can be written as ±9.
-
What is the principal square root?
The principal square root of a number is its positive square root. For example, the principal square root of 81 is 9.
-
What are some methods to calculate square roots?
There are several methods to calculate square roots, including:
- Prime Factorization: Breaking down the number into its prime factors. For example, the prime factors of 81 are \(3 \times 3 \times 3 \times 3\), so \(\sqrt{81} = \sqrt{(3 \times 3) \times (3 \times 3)} = 3 \times 3 = 9\).
- Long Division: A step-by-step approach similar to traditional division.
- Repeated Subtraction: Continuously subtracting odd numbers from the original number until you reach zero. The number of subtractions needed is the square root.
- Using a Calculator: The most straightforward method for non-perfect squares.
-
What are imaginary numbers in relation to square roots?
When dealing with negative numbers under the square root symbol, we encounter imaginary numbers. For example, \(\sqrt{-1}\) is represented as \(i\), where \(i\) is the imaginary unit.
Căn Bậc Hai Của 81: Hướng Dẫn Toàn Diện
READ MORE:
Căn Bậc Hai Của 81 #shorts #toán #toán học #toán học