Can You Square Root 0? Exploring the Simple Yet Fascinating Answer

The concept of taking the square root of a number is fundamental in mathematics. Here, we explore the square root of 0, a unique and intriguing number.

Can You Square Root 0?

Yes, you can take the square root of 0. In fact, the square root of 0 is 0. This is because 0 multiplied by itself (0 * 0) equals 0.

Mathematical Explanation

The square root of a number x is a value y such that:

\[
y^2 = x
\]

For x = 0:

\[
y^2 = 0
\]

Clearly, the value of y that satisfies this equation is 0.

Properties of the Square Root of 0

• Uniqueness: The square root of 0 is unique and is always 0.
• Non-Negativity: The square root of any non-negative number, including 0, is also non-negative.
• Simplicity: It is one of the simplest operations in mathematics since it involves no complex calculations.

Applications

Understanding the square root of 0 can be useful in various mathematical contexts, including:

1. Algebra: Solving equations that involve square roots.
2. Calculus: Evaluating limits and derivatives where 0 might appear under a square root.
3. Engineering: Applying mathematical principles where zero values are critical, such as in control systems.

Conclusion

In summary, the square root of 0 is 0, a straightforward and essential concept in mathematics. This knowledge helps build a foundation for more complex mathematical and scientific studies.

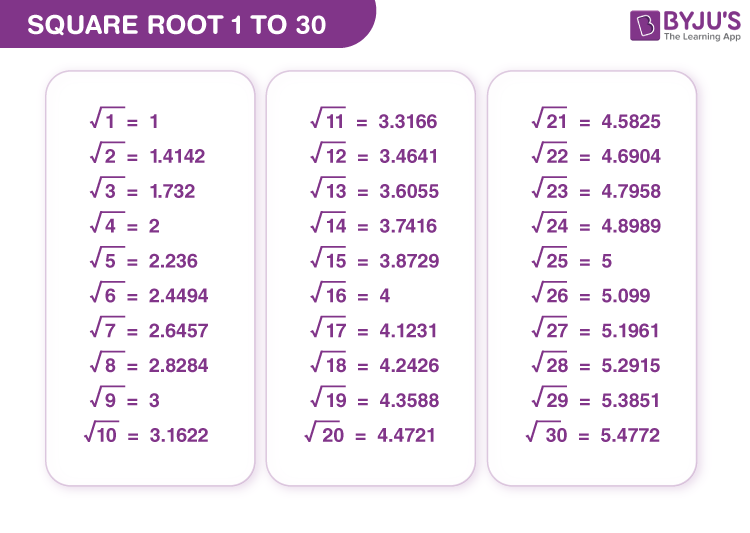
The concept of square roots is fundamental in mathematics, offering a way to understand how numbers relate to each other when multiplied. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 × 3 = 9.

Mathematically, the square root of a number \( x \) is denoted as \( \sqrt{x} \). Here are the key aspects to understand about square roots:

• Definition: If \( y \) is the square root of \( x \), then \( y^2 = x \).
• Non-negative values: By convention, the square root of a non-negative number is always non-negative. For instance, \( \sqrt{16} = 4 \), not -4, even though (-4)² = 16.
• Principal square root: The principal square root is the non-negative square root of a number, which is typically referred to simply as the square root.
• Perfect squares: Numbers like 1, 4, 9, 16, etc., whose square roots are integers, are known as perfect squares.

To further illustrate the process of finding square roots, consider the following steps:

1. Identify the number: Determine the number for which you need to find the square root.
2. Factorization (if needed): For perfect squares, factorizing the number can simplify the process. For example, to find the square root of 36, recognize that 36 = 6 × 6.
3. Use mathematical tools: For non-perfect squares, use tools like the square root function on a calculator or numerical methods for approximation.

Understanding square roots is crucial for solving quadratic equations, understanding geometric properties, and applying mathematical concepts in various fields, including science and engineering.

The square root of a number is a value that, when multiplied by itself, results in the original number. For zero, this concept remains simple and straightforward. Let's explore why the square root of 0 is 0 through a detailed, step-by-step explanation.

Mathematically, the square root of 0 is represented as \( \sqrt{0} \). Here are the key points to understand:

• Basic Definition: The square root of 0 is the number which, when squared, equals 0. In equation form: \[ y^2 = 0 \] The only value of \( y \) that satisfies this equation is 0.
• Uniqueness: Unlike other numbers, zero has only one square root, which is itself. For example, the number 4 has two square roots: 2 and -2. But for 0, there is only one possible square root, which is 0.
• Non-negativity: By definition, the principal square root is always non-negative. Therefore, \( \sqrt{0} \) is non-negative, resulting in 0.

To better understand this, consider the following steps:

1. Identify the Number: Here, the number is 0.
2. Apply the Square Root Operation: To find the square root, determine the number which, when squared, gives 0.
3. Verification: Check by squaring the result: \[ 0^2 = 0 \] This confirms that the square root of 0 is indeed 0.

Understanding the square root of 0 is essential as it forms the basis for more complex mathematical concepts. It demonstrates the simplicity and consistency of mathematical principles, even when dealing with the unique properties of zero.

To fully grasp the concept of the square root of 0, it's important to understand the mathematical definition and explanation of square roots in general. A square root of a number \( x \) is a value \( y \) such that:

\[
y^2 = x
\]

For the specific case of 0, the equation becomes:

\[
y^2 = 0
\]

This means that \( y \) must be 0 because 0 is the only number that, when squared, equals 0. Thus, the square root of 0 is 0. Let's break this down further:

• Definition: The square root of a number \( x \) is a value that, when multiplied by itself, yields \( x \).
• Principal Square Root: By convention, the principal square root is the non-negative root. For any non-negative number \( x \), \( \sqrt{x} \) is non-negative.
• Unique Value for 0: The number 0 is unique in that it has only one square root, which is 0 itself. For example:
  • \( \sqrt{16} = 4 \) or \(-4\), because \( 4^2 = 16 \) and \((-4)^2 = 16 \).
  • \( \sqrt{0} = 0 \), because \( 0^2 = 0 \).

To provide a step-by-step explanation:

1. Identify the Number: Determine the number for which you need to find the square root. Here, the number is 0.
2. Formulate the Equation: Write the equation \( y^2 = x \), substituting 0 for \( x \), giving \( y^2 = 0 \).
3. Solve for \( y \): Find the value of \( y \) that satisfies the equation. The solution is \( y = 0 \) since 0 is the only number that satisfies \( y^2 = 0 \).

The simplicity of this mathematical definition and explanation highlights the consistent and logical structure of mathematics. Understanding why the square root of 0 is 0 reinforces foundational mathematical concepts and aids in the comprehension of more advanced topics.

The square root of a number is a value that, when multiplied by itself, equals the original number. To prove that the square root of 0 is 0, we can use several mathematical approaches. Here is a detailed, step-by-step proof:

1. Basic Definition of Square Root:

   By definition, the square root of a number \( x \) is a number \( y \) such that:

   \[
   y^2 = x
   \]

   For \( x = 0 \), we need to find \( y \) such that:

   \[
   y^2 = 0
   \]

2. Solving the Equation:

   To find the value of \( y \), we solve the equation \( y^2 = 0 \). The only number that satisfies this equation is 0 because:

   \[
   0^2 = 0
   \]

3. Verification through Substitution:

   We can verify the solution by substituting \( y = 0 \) back into the original equation:

   \[
   y^2 = 0 \implies 0^2 = 0
   \]

   This confirms that 0 is indeed the square root of 0.

4. Uniqueness of the Solution:

   For any number \( x \geq 0 \), the principal square root is the non-negative solution. Since 0 is neither positive nor negative, it has a unique square root, which is itself.

5. Graphical Proof:

   Consider the function \( f(y) = y^2 \). This is a parabolic curve that opens upwards. The vertex of this parabola is at the origin (0,0). At this point, the value of \( y \) is 0, and \( f(0) = 0 \). Hence, the square root of 0 is 0.

This comprehensive proof demonstrates that the square root of 0 is 0 through multiple mathematical approaches, reinforcing the consistency and simplicity of this fundamental concept.

The square root of 0, while seemingly simple, has a range of practical applications in various fields of mathematics, science, and engineering. Understanding how and why it is used can shed light on its importance. Here are some practical applications of the square root of 0:

• Solving Quadratic Equations:

  In quadratic equations of the form \( ax^2 + bx + c = 0 \), the discriminant (\( b^2 - 4ac \)) determines the nature of the roots. If the discriminant is 0, the equation has a repeated real root. For example:
  \[
  x^2 - 2x + 1 = 0 \implies x = 1
  \]
  Here, the square root of the discriminant (0) plays a critical role in determining the roots.

• Calculus and Limits:

  The square root of 0 is often encountered in calculus, especially when evaluating limits. It simplifies expressions and helps in solving limit problems. For instance:
  \[
  \lim_{{x \to 0}} \sqrt{x^2} = \sqrt{0} = 0
  \]
  This property is useful in simplifying complex limit calculations.

• Physics and Engineering:

  In physics and engineering, the square root of 0 is used in various calculations involving motion, energy, and other physical phenomena. For instance, in equations describing the potential energy of a system, where displacement might be zero, the square root of 0 simplifies the calculations.

• Graphical Representations:

  In graphing functions, understanding the behavior of the square root of 0 helps in plotting accurate graphs. For example, the graph of \( y = \sqrt{x} \) starts at the origin (0,0), highlighting the role of the square root of 0 in the graph.

• Algorithm Design:

  In computer science and algorithm design, the concept of the square root of 0 can be used in various computational algorithms, especially those involving optimizations and boundary conditions. It ensures that algorithms handle cases involving zero correctly.

• Mathematical Proofs:

  The square root of 0 is often used in mathematical proofs to establish certain properties or to simplify equations. Its straightforward nature makes it a handy tool in theoretical mathematics.

These applications illustrate the importance of understanding the square root of 0 and its role in simplifying and solving various mathematical and practical problems. Its simplicity and consistency make it a fundamental concept in multiple domains.

The concept of square roots extends beyond basic arithmetic and finds applications in various branches of mathematics. Here, we explore how square roots, including the square root of 0, are utilized in different mathematical fields:

• Algebra:

  In algebra, square roots are used to solve quadratic equations, simplify expressions, and factor polynomials. For instance, solving the equation \( x^2 = 0 \) directly shows that \( x = 0 \), demonstrating the utility of the square root of 0 in simplifying solutions.

• Geometry:

  Square roots appear frequently in geometry, particularly in the context of the Pythagorean theorem, which relates the lengths of the sides of a right triangle. The distance formula, which is derived from the Pythagorean theorem, uses square roots to determine the distance between two points in a plane. When the points coincide, the distance is zero, and the square root of 0 is relevant.

• Calculus:

  In calculus, square roots are essential in solving limits, derivatives, and integrals. For example, the derivative of \( \sqrt{x} \) requires understanding the behavior of square roots. Additionally, when evaluating certain limits, the square root of 0 can simplify expressions, such as:
  \[
  \lim_{{x \to 0}} \sqrt{x} = 0

• Complex Numbers:

  Square roots play a crucial role in complex numbers. The square root of a negative number introduces the imaginary unit \( i \), where \( i^2 = -1 \). The concept extends to 0, where the square root of 0 remains 0 even in the complex plane:
  \[
  \sqrt{0 + 0i} = 0

• Number Theory:

  In number theory, square roots are used to explore properties of integers, prime numbers, and modular arithmetic. For example, the Legendre symbol and quadratic residues involve the concept of square roots, including the square root of 0 in modular systems.

• Linear Algebra:

  Square roots are also significant in linear algebra, especially in the context of eigenvalues and eigenvectors. The spectral theorem, which involves decomposing a matrix into orthogonal components, often includes square root calculations. When dealing with zero eigenvalues, the square root of 0 is relevant:
  \[
  \sqrt{\lambda} = 0 \text{ when } \lambda = 0

These examples illustrate the diverse applications of square roots across various mathematical fields. Understanding how to handle the square root of 0 within these contexts highlights its importance and utility in both theoretical and applied mathematics.

In algebra, the concept of the square root is fundamental, particularly when discussing real numbers. The square root of a number x is a value y such that:

\( y^2 = x \)

For non-negative real numbers, the principal square root is the non-negative value of y that satisfies this equation. The square root of 0, denoted as \( \sqrt{0} \), is a special case with unique properties.

Mathematical Explanation

The square root of 0 is 0 because:

\( 0^2 = 0 \)

In simpler terms, there is no other number except 0 that when squared results in 0.

Properties of \( \sqrt{0} \)

• Uniqueness: The square root of 0 is uniquely 0. Unlike other non-zero numbers that have two square roots (positive and negative), 0 has only one square root.
• Non-negativity: As the principal square root is always non-negative, \( \sqrt{0} \) is 0 and not -0, as -0 is equivalent to 0.

Applications in Algebra

Understanding \( \sqrt{0} \) is essential in various algebraic contexts:

1. Solving Equations: When solving quadratic equations of the form \( x^2 = a \), if a is 0, the solution is \( x = 0 \). This simplifies solving such equations since no additional roots need to be considered.
2. Radicals and Simplification: In simplifying expressions involving square roots, knowing that \( \sqrt{0} = 0 \) helps to simplify terms directly, avoiding unnecessary complexity.

Example in Algebraic Context

Consider the equation:

\( x^2 = 0 \)

To find the value of \( x \), take the square root of both sides:

\( x = \sqrt{0} \)

Thus, \( x = 0 \) is the only solution.

Key Takeaways

• The square root of 0 is 0.
• In algebra, this concept is used in simplifying equations and expressions.
• It has unique properties making it simpler to handle compared to other non-zero numbers.

In calculus, understanding the square root of 0 is crucial when dealing with limits, derivatives, and integrals. This concept is foundational, influencing how we approach various problems involving continuous functions and their behaviors at specific points.

Limits Involving \( \sqrt{0} \)

One of the key areas where the square root of 0 appears in calculus is in the evaluation of limits. For instance, consider a function \( f(x) = \sqrt{x} \). As \( x \) approaches 0 from the right, we analyze the limit:

\( \lim_{{x \to 0^+}} \sqrt{x} = 0 \)

This indicates that as \( x \) gets closer to 0, the function \( \sqrt{x} \) approaches 0.

Derivatives and \( \sqrt{0} \)

The concept of \( \sqrt{0} \) also plays a role in differentiation. Consider the derivative of \( f(x) = \sqrt{x} \). Using the power rule for differentiation, we write:

\( f(x) = x^{1/2} \)

Applying the power rule \( \frac{d}{dx} [x^n] = n x^{n-1} \), we get:

\( f'(x) = \frac{1}{2} x^{-1/2} \)

At \( x = 0 \), the derivative \( f'(0) \) involves \( x^{-1/2} \), which becomes undefined as \( x \) approaches 0. However, for the purpose of understanding \( \sqrt{0} \), this highlights the special behavior at this point.

Integrals Involving \( \sqrt{0} \)

In integration, the square root of 0 appears when we evaluate definite integrals with limits approaching 0. For example, consider the integral:

\( \int_0^a \sqrt{x} \, dx \)

To solve this, we use the power rule for integration:

\( \int x^{n} \, dx = \frac{x^{n+1}}{n+1} \)

Applying this to our integral:

\( \int_0^a x^{1/2} \, dx = \left. \frac{2}{3} x^{3/2} \right|_0^a \)

Evaluating this at the bounds, we get:

\( \frac{2}{3} a^{3/2} - \frac{2}{3} \cdot 0^{3/2} = \frac{2}{3} a^{3/2} \)

This integral is finite and valid, showing that \( \sqrt{0} = 0 \) is handled smoothly in integration.

Behavior at the Origin

In calculus, we often examine the behavior of functions at specific points, especially around the origin (0,0). The function \( f(x) = \sqrt{x} \) is continuous at \( x = 0 \), meaning:

\( \lim_{{x \to 0}} \sqrt{x} = \sqrt{0} = 0 \)

Continuity at 0 indicates that the function does not have any abrupt changes at this point.

Applications and Implications

Understanding the square root of 0 in calculus is essential for analyzing and solving problems involving:

• Rate of Change: Derivatives and their applications in physics and engineering often involve evaluating functions at 0.
• Area Under Curves: Integrals that include limits at 0 are common in calculating areas and volumes.
• Continuous Functions: Understanding the behavior of continuous functions at the origin helps in modeling real-world phenomena.

Conclusion

The square root of 0 in calculus is a simple yet powerful concept that assists in understanding more complex behaviors of functions. Its applications span across evaluating limits, derivatives, and integrals, making it a cornerstone in the study of calculus.

In engineering, the concept of the square root of 0 (\( \sqrt{0} \)) is fundamental, especially in the context of systems analysis, signal processing, and various other practical applications. Understanding how \( \sqrt{0} \) influences calculations and system behaviors is crucial for designing and analyzing engineering solutions.

Electrical Engineering

In electrical engineering, \( \sqrt{0} \) often appears in the analysis of circuits and signal processing. Consider the impedance \( Z \) of an ideal short circuit. The impedance is defined as:

\( Z = \sqrt{R^2 + (X_L - X_C)^2} \)

Where \( R \) is resistance, \( X_L \) is inductive reactance, and \( X_C \) is capacitive reactance. In the case of a short circuit, all these components are zero, so:

\( Z = \sqrt{0^2 + (0 - 0)^2} = \sqrt{0} = 0 \)

This indicates that the impedance in a short circuit is zero, a critical factor in circuit design and safety analysis.

Mechanical Engineering

In mechanical engineering, \( \sqrt{0} \) can be seen in the context of vibrational analysis. For example, consider the natural frequency of a damped harmonic oscillator, which is given by:

\( \omega = \sqrt{\frac{k}{m} - \frac{b^2}{4m^2}} \)

Where \( k \) is the stiffness, \( m \) is the mass, and \( b \) is the damping coefficient. If the damping coefficient \( b \) is such that:

\( \frac{b^2}{4m^2} = \frac{k}{m} \)

Then the expression under the square root becomes zero:

\( \omega = \sqrt{0} = 0 \)

This scenario describes critical damping, where the system returns to equilibrium without oscillating. It's a vital consideration in designing systems to avoid excessive vibrations.

Control Systems

In control engineering, the square root of 0 plays a role in determining the stability and response of systems. For instance, the characteristic equation of a control system might lead to roots that indicate the system's behavior. If the system's poles are at zero, this often represents a specific type of system response such as a step response in a first-order system:

\( H(s) = \frac{K}{s} \)

The square root of the poles being zero indicates a steady-state behavior or a particular form of response without oscillations, which is critical for understanding how a system reacts over time.

Civil Engineering

In civil engineering, the square root of 0 can be relevant in structural analysis, especially in evaluating critical load conditions. For instance, the buckling load of a column is given by:

\( P_{cr} = \frac{\pi^2 EI}{(KL)^2} \)

If the effective length factor \( K \) is such that \( K = 0 \), the critical load \( P_{cr} \) approaches zero:

\( P_{cr} = \frac{\pi^2 EI}{(0)^2} = 0 \)

This implies that the column can buckle with negligible load, which is crucial in ensuring that structures are designed with adequate stability and load-bearing capacity.

Signal Processing

In signal processing, \( \sqrt{0} \) is significant when analyzing signals that pass through filters or when determining the magnitude of zero-frequency components (DC components). The root mean square (RMS) value of a signal is often used to measure its effective value:

\( \text{RMS} = \sqrt{\frac{1}{T} \int_0^T x(t)^2 \, dt} \)

If \( x(t) \) represents a signal that is zero over the interval, then the RMS value is:

\( \text{RMS} = \sqrt{0} = 0 \)

This can indicate that the signal has no power or is absent over the given period, which is crucial for signal analysis and noise reduction.

Summary

In engineering, the square root of 0 is more than a mathematical curiosity; it has practical implications in various fields. From circuit design and vibrational analysis to structural stability and signal processing, understanding \( \sqrt{0} \) helps engineers design, analyze, and ensure the safety and effectiveness of systems and structures.

The square root of 0 (\( \sqrt{0} \)) is a straightforward concept in mathematics, but several misconceptions about it persist. Understanding these can help clarify its true properties and applications.

Misconception 1: The Square Root of 0 is Undefined

Some people believe that the square root of 0 is undefined or does not exist. However, this is not true. Mathematically, the square root of 0 is well-defined and equals 0:

\( \sqrt{0} = 0 \)

This follows from the definition of the square root. Since 0 is the only number that, when squared, equals 0 (\( 0 \times 0 = 0 \)), \( \sqrt{0} \) is unambiguously 0.

Misconception 2: The Square Root of 0 Can Be Positive or Negative

There is a common confusion that the square root of any number, including 0, can be positive or negative. While it's true that numbers like \( \sqrt{4} \) have both positive and negative square roots (\( \pm 2 \)), the principal (non-negative) square root is typically considered. For 0, there is no distinction:

\( \sqrt{0} = 0 \)

Since 0 has no sign, it cannot be positive or negative. The concept of negative zero is not used in standard mathematics.

Misconception 3: The Square Root of 0 Leads to Division by Zero Problems

Another misconception is that using \( \sqrt{0} \) in calculations can lead to division by zero errors. However, this misunderstanding conflates different mathematical issues. The expression \( \sqrt{0} \) itself is simply 0 and does not cause division by zero. Problems only arise if you try to divide by \( \sqrt{0} \), as dividing by zero is undefined:

\(\frac{1}{\sqrt{0}} = \frac{1}{0} \) (undefined)

Therefore, the square root of 0 itself does not inherently lead to undefined operations; issues only arise when it is used as a divisor.

Misconception 4: The Square Root of 0 is Meaningless in Practical Applications

Some believe that \( \sqrt{0} \) has no practical use or meaning. In reality, it plays a vital role in various fields such as engineering, physics, and economics. For example, in signal processing, \( \sqrt{0} \) can represent the zero energy state of a signal. In mechanical systems, it can indicate a state with no motion or energy at a given point.

Misconception 5: The Square Root of 0 is Not Covered in Basic Math Education

There is a belief that \( \sqrt{0} \) is an advanced topic not covered in elementary mathematics. However, the square root of 0 is introduced early in mathematics education when students learn about square roots and basic properties of numbers. It is often one of the first examples given because it simplifies easily and helps establish the concept of roots.

Clarifying the Truth

Understanding \( \sqrt{0} \) is straightforward when you remember that:

• \( \sqrt{0} = 0 \) is a well-defined and real number.
• It does not have a positive or negative form.
• It does not inherently cause division by zero problems.
• It has practical applications in various scientific and engineering fields.
• It is a basic concept introduced early in mathematics education.

By dispelling these misconceptions, we can appreciate the simplicity and utility of the square root of 0 in both theoretical and practical contexts.

The concept of the square root of 0 often raises questions. Below, we address some of the most frequently asked questions to clarify common doubts and misconceptions.

1. What is the square root of 0?

The square root of 0 is 0. Mathematically, this is because 0 is the only number that, when multiplied by itself, gives 0:

\( \sqrt{0} = 0 \)

2. Is the square root of 0 positive or negative?

The square root of 0 is neither positive nor negative; it is simply 0. Zero is considered a neutral number, having no positive or negative value.

3. Can you divide by the square root of 0?

No, you cannot divide by the square root of 0. Since \( \sqrt{0} = 0 \), and division by 0 is undefined in mathematics, any expression that involves dividing by \( \sqrt{0} \) is also undefined:

\(\frac{1}{\sqrt{0}} = \frac{1}{0} \) (undefined)

4. Why is the square root of 0 not considered undefined?

The square root of 0 is not considered undefined because there exists a unique real number (0) that satisfies the equation \( x^2 = 0 \). Since 0 multiplied by itself equals 0, \( \sqrt{0} \) is defined as 0.

5. How is the square root of 0 used in calculus?

In calculus, the square root of 0 is used in limits, derivatives, and integrals. For example, when finding the limit of \( \sqrt{x} \) as \( x \) approaches 0 from the right, the result is 0:

\( \lim_{{x \to 0^+}} \sqrt{x} = 0 \)

It also appears in evaluating the behavior of functions at specific points, such as the zero frequency component in signal processing.

6. What is the significance of the square root of 0 in engineering?

In engineering, \( \sqrt{0} \) often appears in contexts like analyzing circuit impedance, determining stability in control systems, or understanding vibrational modes in mechanical structures. It represents a state with no energy or movement, such as in a critically damped system.

7. How does the square root of 0 apply in real-world scenarios?

The square root of 0 can represent a point where no change or activity occurs. For instance, in economics, it could describe a situation with zero growth rate, or in physics, a state with no kinetic energy. Understanding \( \sqrt{0} \) helps simplify models and predict system behavior accurately.

8. Is there any difference between \( \sqrt{0} \) and \(-\sqrt{0} \)?

There is no difference between \( \sqrt{0} \) and \(-\sqrt{0} \) because both are equal to 0. Unlike other non-zero numbers, 0 does not have positive or negative counterparts.

9. How is \( \sqrt{0} \) introduced in education?

The concept of \( \sqrt{0} \) is introduced early in mathematics education, typically when students first learn about square roots. It's a fundamental example used to illustrate the basic property that the square root of a number is a value that, when squared, returns the original number.

10. Can the square root of 0 be used in scientific notation?

While the square root of 0 is generally just 0, in scientific notation, it can be written as \( 0 \times 10^n \), where \( n \) is any integer. However, since 0 multiplied by any power of 10 is still 0, this is typically simplified to just 0.

Summary

The square root of 0 is a simple yet significant concept in mathematics and its applications. By understanding its properties and implications, we can better grasp its role in various fields and practical scenarios.