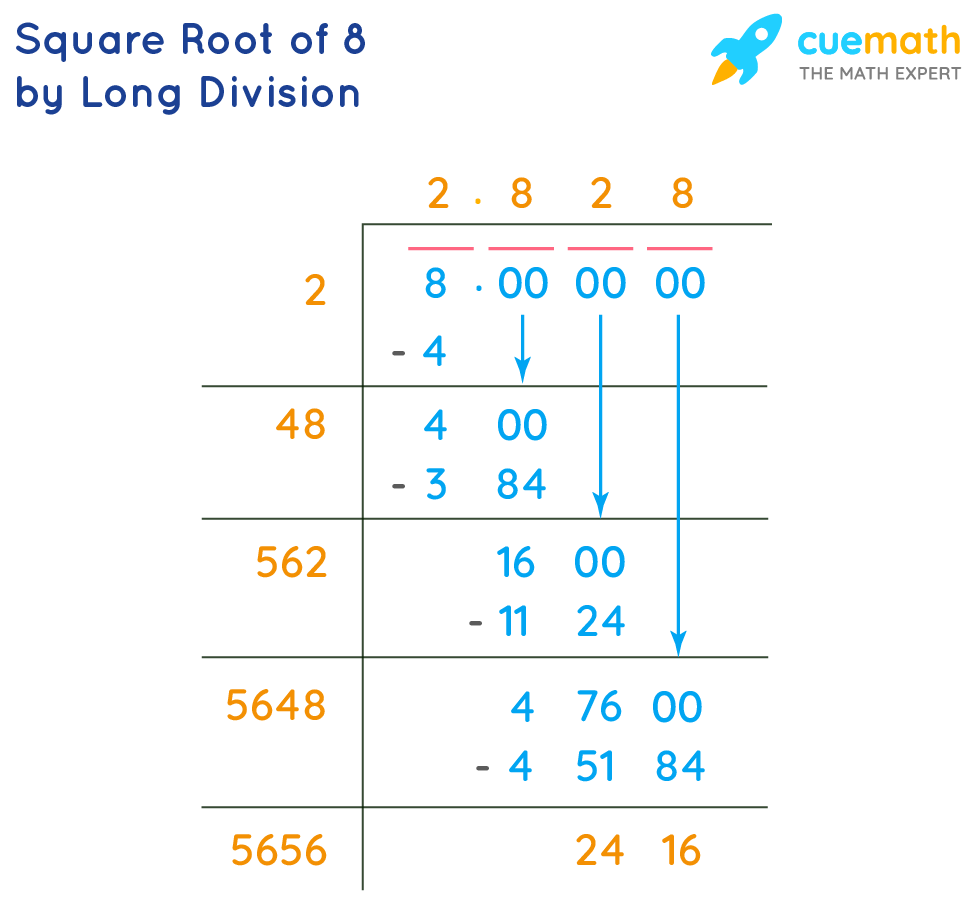
Topic is the square root of 0 a real number: The square root of 0 is indeed a real number and a fundamental concept in mathematics. Understanding why this is true can clarify broader mathematical principles and address common misconceptions. This article explores the nature of 0’s square root, providing clear explanations and practical examples to deepen your comprehension of real numbers.
Table of Content
- Is the Square Root of 0 a Real Number?
- Introduction to Square Roots
- What is the Square Root of 0?
- Mathematical Explanation of the Square Root of 0
- Real Numbers: Definition and Properties
- Why the Square Root of 0 is a Real Number
- Visual Representation of Square Roots Including 0
- Square Root of 0 in Various Mathematical Contexts
- Common Misconceptions About the Square Root of 0
- Applications and Implications of the Square Root of 0
- Summary and Key Takeaways
- Further Reading and Resources
- YOUTUBE: Xem video để hiểu Square Roots là gì, được giảng dạy bởi Thầy J. Giải thích một cách đơn giản và dễ hiểu về khái niệm này.
Is the Square Root of 0 a Real Number?
The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). Mathematically, this is represented as:
\[ \sqrt{x} \]
Understanding the Square Root of 0
For the number 0, this can be represented as:
\[ \sqrt{0} = 0 \]
This is because 0 multiplied by 0 equals 0:
\[ 0 \times 0 = 0 \]
Therefore, the square root of 0 is indeed 0, making it a real number. Real numbers include all the rational and irrational numbers, and 0 is part of this set.
Properties of Square Roots
- The square root of a non-negative number is always non-negative.
- The square root of 0 is unique and is the only number whose square root is itself.
- Square roots of positive numbers are always positive.
Examples
To further understand the concept of square roots, here are some examples:
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
Practice Problems
- Find the square root of 25.
- \[ \sqrt{25} = 5 \]
- Find the square root of 49.
- \[ \sqrt{49} = 7 \]
- Find the square root of 64.
- \[ \sqrt{64} = 8 \]
Conclusion
In conclusion, the square root of 0 is a real number. It is 0, which fits neatly within the set of real numbers. Understanding this concept helps in grasping more complex mathematical ideas and solving various mathematical problems effectively.

READ MORE:
Introduction to Square Roots
Square roots are fundamental in mathematics, representing a number that, when multiplied by itself, yields the original number. For instance, the square root of 9 is 3, because \(3 \times 3 = 9\). The notation for the square root of a number \(x\) is \(\sqrt{x}\), where \(x\) is known as the radicand.
Here are key properties and examples of square roots:
- Positive Numbers: For any positive number, the square root is also positive. Example: \(\sqrt{16} = 4\).
- Zero: The square root of 0 is 0. This is because \(0 \times 0 = 0\).
- Negative Numbers: Negative numbers do not have real square roots because no real number multiplied by itself gives a negative product. The square roots of negative numbers are represented using imaginary numbers.
The concept can be extended as follows:
- Perfect Squares: Numbers like 1, 4, 9, 16, etc., are perfect squares because their square roots are integers.
- Non-Perfect Squares: Numbers that are not perfect squares have irrational square roots, meaning their decimal representation is non-repeating and non-terminating.
- Operations: Square roots are used in various mathematical operations and real-world applications, from solving quadratic equations to calculating areas in geometry.
Understanding square roots is essential for progressing in higher mathematics and is a building block for various mathematical concepts and operations.
What is the Square Root of 0?
The square root of 0, denoted as \(\sqrt{0}\), is a unique and straightforward concept in mathematics. To understand it fully, consider the definition of a square root: for any number \(x\), \(\sqrt{x}\) is a number \(y\) such that \(y^2 = x\). Applying this definition to 0, we have:
- Definition: The square root of 0 is a number that, when squared, equals 0. Mathematically, if \(y = \sqrt{0}\), then \(y^2 = 0\).
- Calculation: Since the only number that satisfies \(y^2 = 0\) is 0 itself, we conclude that \(\sqrt{0} = 0\).
- Real Number Property: The result \(0\) is a real number because it belongs to the set of real numbers \(\mathbb{R}\), which includes all rational and irrational numbers, as well as 0.
Here’s a visual representation of the concept:
| Radicand (\(x\)) | Square Root (\(\sqrt{x}\)) | Verification (\(\sqrt{x} \times \sqrt{x}\)) |
|---|---|---|
| 0 | 0 | 0 |
| 4 | 2 | 4 |
| 9 | 3 | 9 |
This table shows that for any non-negative number \(x\), its square root is a number that squares back to \(x\). In the case of 0, its square root is 0, confirming the mathematical consistency and the fact that \(\sqrt{0}\) is a real number.
The square root of 0 plays a vital role in various mathematical and real-world applications, reinforcing the foundational principles of arithmetic and algebra.
Mathematical Explanation of the Square Root of 0
The square root of 0, denoted \(\sqrt{0}\), is a fundamental concept in mathematics with a straightforward explanation. Here's a step-by-step breakdown:
- Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). Formally, \(y = \sqrt{x}\) if and only if \(y^2 = x\).
- Application to 0: Applying the definition to 0, we seek a number \(y\) for which \(y^2 = 0\). This equation simplifies to:
- \(y \times y = 0\)
- Since the only number that satisfies this equation is 0, it follows that \(y = 0\).
- Conclusion: Therefore, the square root of 0 is 0, written as \(\sqrt{0} = 0\).
To further illustrate, consider the general properties of square roots:
- Non-negativity: For any non-negative number \(x\), the principal (non-negative) square root is non-negative.
- Uniqueness: For each non-negative number \(x\), there is exactly one non-negative square root. In this case, 0 is unique because:
- Only \(0 \times 0 = 0\).
- Consistency: The function \(f(x) = \sqrt{x}\) is consistent with basic arithmetic operations. Hence, \(\sqrt{0}\) fits naturally into the set of real numbers.
Here is a summary table showing square roots of various numbers, including 0:
| Number (\(x\)) | Square Root (\(\sqrt{x}\)) | Verification (\(\sqrt{x} \times \sqrt{x}\)) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 4 | 2 | 4 |
| 9 | 3 | 9 |
Understanding the square root of 0 clarifies its role in broader mathematical contexts, demonstrating that \(\sqrt{0} = 0\) is both logical and consistent within the real number system.
Real Numbers: Definition and Properties
Real numbers are a fundamental set in mathematics, encompassing all numbers that can be found on the number line. They include rational and irrational numbers, each having unique properties. Here's an in-depth look at the definition and properties of real numbers:
- Definition:
- Real numbers, denoted by \(\mathbb{R}\), include all numbers that can be represented on the number line, encompassing both rational and irrational numbers.
- Formally, a real number is any value that represents a quantity along a continuous line, including positive numbers, negative numbers, and zero.
- Classification:
- Rational Numbers: These are numbers that can be expressed as the quotient of two integers \( \frac{p}{q} \), where \( p \) and \( q \) are integers and \( q \neq 0 \). Examples include \( \frac{1}{2} \), 3, and -4.
- Irrational Numbers: Numbers that cannot be expressed as a simple fraction. Their decimal expansions are non-repeating and non-terminating. Examples include \( \sqrt{2} \), \( \pi \), and \( e \).
- Properties:
- Ordering: Real numbers can be arranged in a sequential order on the number line, allowing for comparisons (greater than, less than).
- Density: Between any two real numbers, there is always another real number. This property demonstrates the continuity of the real number line.
- Arithmetic Operations: Real numbers are closed under addition, subtraction, multiplication, and division (except division by zero). These operations are well-defined for all real numbers.
- Completeness: Every non-empty set of real numbers that is bounded above has a least upper bound (supremum). This property distinguishes real numbers from rational numbers.
To understand how real numbers encompass both rational and irrational numbers, consider the following examples:
| Type | Examples | Characteristics |
|---|---|---|
| Rational Numbers | \( \frac{1}{3}, -2, 0.75 \) | Can be expressed as fractions, terminating or repeating decimals. |
| Irrational Numbers | \( \sqrt{3}, \pi, \ln(2) \) | Cannot be expressed as fractions, non-terminating and non-repeating decimals. |
The inclusion of zero in the set of real numbers is crucial as it acts as the additive identity, meaning any real number added to zero remains unchanged. In the context of square roots, the real number system supports the existence of non-negative square roots for non-negative numbers, validating that \(\sqrt{0} = 0\).
Understanding the real number system is essential for grasping more complex mathematical concepts, as it forms the basis for continuous quantities and many fundamental theorems in mathematics.

Why the Square Root of 0 is a Real Number
The square root of 0, denoted as \(\sqrt{0}\), is considered a real number for several logical and mathematical reasons. Here's a step-by-step explanation:
- Definition of Square Roots:
- By definition, the square root of a number \(x\) is a number \(y\) such that \(y^2 = x\).
- For \(x = 0\), we need \(y\) such that \(y^2 = 0\).
- Solution:
- The only number \(y\) that satisfies \(y^2 = 0\) is 0 itself.
- Thus, \(\sqrt{0} = 0\).
- Real Number Criteria:
- A real number is any value that can represent a quantity along the number line, including rational and irrational numbers, as well as 0.
- Since 0 is a value on the number line, it meets the criteria for being a real number.
- Properties of Real Numbers:
- Closure: The set of real numbers is closed under addition, subtraction, multiplication, and non-zero division. 0 being the square root of itself adheres to this property.
- Identity: In real numbers, 0 is the additive identity, meaning \(a + 0 = a\) for any real number \(a\). This makes 0 a fundamental part of the real number system.
- Mathematical Verification:
- The function \(f(x) = \sqrt{x}\) is defined for all non-negative real numbers, including 0.
- Graphically, the square root function starts at the origin (0,0), confirming that the square root of 0 is a valid and real number.
Below is a verification table that reinforces why the square root of 0 is real:
| Number (\(x\)) | Square Root (\(\sqrt{x}\)) | Verification (\(\sqrt{x} \times \sqrt{x}\)) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 4 | 2 | 4 |
| 9 | 3 | 9 |
In conclusion, \(\sqrt{0} = 0\) is logically consistent and aligns perfectly with the definition and properties of real numbers. Its inclusion in the set of real numbers highlights its importance in arithmetic and algebraic contexts, confirming its status as a real number.
Visual Representation of Square Roots Including 0
Understanding the square roots of numbers, including 0, can be enhanced through visual representation. Here, we explore the graphical and tabular illustration of square roots:
- Graph of the Square Root Function:
The square root function \(f(x) = \sqrt{x}\) can be plotted on a coordinate plane. This function is defined for all non-negative \(x\), starting from the origin (0,0). Below is the graph of \(y = \sqrt{x}\):

- The graph starts at (0,0), indicating that the square root of 0 is 0.
- As \(x\) increases, \(y\) increases, but at a decreasing rate, forming a curve that rises gradually.
- Number Line Representation:
On a number line, the square roots of perfect squares fall at specific points. For example:
- \(\sqrt{0}\) is located at 0.
- \(\sqrt{1} = 1\) is located at 1.
- \(\sqrt{4} = 2\) is located at 2.

- Table of Square Roots:
A table showing the square roots of selected non-negative numbers helps illustrate the relationship:
Number (\(x\)) Square Root (\(\sqrt{x}\)) Verification (\(\sqrt{x} \times \sqrt{x}\)) 0 0 0 1 1 1 4 2 4 9 3 9 16 4 16 - Area Interpretation:
Square roots can also be interpreted through the area of squares:
- The side length of a square with area \(0\) is \(\sqrt{0}\), which is 0.
- For a square with area \(4\), the side length is \(\sqrt{4} = 2\).

These visual aids help solidify the understanding that \(\sqrt{0} = 0\) is logically consistent and aligns well with the graphical, numerical, and geometric interpretations of square roots.
Square Root of 0 in Various Mathematical Contexts
The square root of 0, denoted as \(\sqrt{0}\), appears in several mathematical contexts, each providing unique insights and applications. Here's a detailed exploration of how \(\sqrt{0}\) fits into different areas of mathematics:
- Arithmetic:
- The fundamental property of square roots is that for any non-negative number \(x\), the square root \(\sqrt{x}\) is also non-negative.
- For \(x = 0\), \(\sqrt{0} = 0\), adhering to the basic rule that \(y^2 = 0\) implies \(y = 0\).
- Algebra:
- In algebra, solving the equation \(x^2 = 0\) leads directly to \(x = 0\), demonstrating that \(\sqrt{0} = 0\).
- This solution is essential in simplifying polynomial equations and understanding roots of functions.
- Calculus:
- In calculus, the concept of limits applies to square roots. As \(x\) approaches 0, the limit of \(\sqrt{x}\) is 0, written as \(\lim_{{x \to 0^+}} \sqrt{x} = 0\).
- This property is useful in solving problems involving continuity and differentiability.
- Geometry:
- In geometry, the side length of a square with area 0 is \(\sqrt{0}\), which is 0. This illustrates that a square with no area has no length.
- Similarly, the distance from a point to itself is 0, represented as \(\sqrt{0}\).
- Complex Numbers:
- In the context of complex numbers, while every real number is also a complex number (with an imaginary part of 0), \(\sqrt{0}\) remains 0.
- Thus, the square root of 0 does not gain any complexity when extended into the complex plane.
- Set Theory:
- From a set-theoretic perspective, the square root function maps non-negative real numbers to non-negative real numbers, including the mapping of 0 to 0.
- This ensures the function's completeness and consistency across the set of real numbers \(\mathbb{R}\).
To illustrate these contexts further, consider the following examples and explanations:
| Context | Explanation | Example |
|---|---|---|
| Arithmetic | Square root of non-negative numbers | \(\sqrt{0} = 0\) |
| Algebra | Solving equations \(x^2 = 0\) | \(\sqrt{0} = 0\) |
| Calculus | Limits involving square roots | \(\lim_{{x \to 0^+}} \sqrt{x} = 0\) |
| Geometry | Side length of a square with area 0 | \(\sqrt{0} = 0\) |
| Complex Numbers | Extension into complex plane | \(\sqrt{0} = 0\) |
| Set Theory | Mapping in real number set | \(\sqrt{0} = 0\) |
Understanding the role of \(\sqrt{0}\) across these mathematical contexts reinforces its importance and clarifies why it is both a fundamental and real number.
Common Misconceptions About the Square Root of 0
Despite its simplicity, the square root of 0, \(\sqrt{0}\), is often misunderstood. Here, we address and clarify several common misconceptions:
- Misconception: The Square Root of 0 is Undefined
Clarification: The square root of 0 is defined and is exactly 0. According to the definition of square roots, if \(y = \sqrt{x}\), then \(y^2 = x\). For \(x = 0\), this gives \(y^2 = 0\), which implies \(y = 0\).
- Misconception: The Square Root of 0 is Positive
Clarification: While square roots are typically considered to have a non-negative value, the square root of 0 is exactly 0, neither positive nor negative. It is the point of neutrality on the number line.
- Misconception: The Square Root of 0 is Complex
Clarification: Although complex numbers include a real and imaginary part, \(\sqrt{0}\) is purely real. In the complex number system, it remains 0, as it has no imaginary component.
- Misconception: The Square Root of 0 Changes in Different Contexts
Clarification: The value of \(\sqrt{0}\) remains consistent across various mathematical contexts, whether in arithmetic, algebra, calculus, or complex numbers. It consistently evaluates to 0.
- Misconception: The Square Root of 0 is Not a Real Number
Clarification: Zero is a real number, and so is its square root. The set of real numbers \(\mathbb{R}\) includes all positive numbers, negative numbers, and zero, making \(\sqrt{0}\) a real number.
To further illustrate these clarifications, consider the following table:
| Misconception | Reality |
|---|---|
| The square root of 0 is undefined. | \(\sqrt{0}\) is defined as 0. |
| The square root of 0 is positive. | \(\sqrt{0}\) is neither positive nor negative; it is exactly 0. |
| The square root of 0 is complex. | \(\sqrt{0}\) is purely real and equals 0. |
| The square root of 0 changes with context. | \(\sqrt{0}\) remains 0 in all contexts. |
| The square root of 0 is not a real number. | \(\sqrt{0}\) is a real number. |
These common misconceptions often arise from misunderstandings about the basic properties of square roots and the nature of zero. By clarifying these points, we can better appreciate the simplicity and consistency of \(\sqrt{0} = 0\).
Applications and Implications of the Square Root of 0
The square root of 0, denoted as \( \sqrt{0} \), has several important applications and implications in mathematics and beyond:
- Foundational Concept in Algebra: Understanding \( \sqrt{0} \) is crucial in algebraic contexts, where it serves as a fundamental example in defining properties of square roots and their behaviors.
- Identity Element in Multiplication: \( \sqrt{0} \) acts as the identity element under multiplication in certain algebraic structures, notably in the context of rings and fields, where it plays a pivotal role in defining the structure of these mathematical systems.
- Limiting Case in Calculus: In calculus, the concept of \( \sqrt{0} \) is linked to the study of limits and infinitesimal quantities, providing insights into how functions behave as they approach zero and contributing to foundational concepts in analysis.
- Engineering and Physics Applications: In applied sciences, \( \sqrt{0} \) is encountered in various theoretical and practical contexts, such as signal processing, where it represents specific conditions and boundary cases essential for understanding system behavior.
- Symbolic Representation: Beyond its numerical interpretation, \( \sqrt{0} \) serves symbolically to represent a starting point or a point of origin in theoretical frameworks across disciplines, illustrating zero as a significant reference point.
These applications underscore the broader significance of \( \sqrt{0} \) beyond its elementary definition, highlighting its role in foundational theories and practical computations across mathematics and scientific domains.
Summary and Key Takeaways
After exploring the concept of the square root of 0, several key points emerge:
- Real Number Classification: \( \sqrt{0} \) is indeed a real number, as it satisfies the definition of a real number being a non-negative number that can be represented on the real number line.
- Algebraic and Mathematical Significance: In algebra, \( \sqrt{0} \) serves as a foundational example, illustrating properties of square roots and their behavior under mathematical operations.
- Limiting Case in Calculus: In calculus and analysis, \( \sqrt{0} \) is crucial in understanding limits and infinitesimal quantities, contributing to theories of continuity and differentiability.
- Practical Applications: Beyond theory, \( \sqrt{0} \) finds applications in engineering and physics, where it represents critical boundary conditions and starting points for theoretical models and practical computations.
- Symbolic Representation: Symbolically, \( \sqrt{0} \) represents a significant concept in various disciplines, symbolizing zero as a reference point and illustrating fundamental properties of numbers.
Understanding \( \sqrt{0} \) not only enriches mathematical knowledge but also highlights its pervasive presence across diverse scientific and theoretical frameworks.
Further Reading and Resources
For further exploration of the concept of the square root of 0 and related topics, consider the following resources:
- - Dive deeper into the fundamentals of square roots and their properties.
- - Explore the theoretical underpinnings of real numbers and their applications.
- - Learn how calculus, including concepts like limits involving \( \sqrt{0} \), is applied in engineering disciplines.
- - Understand the symbolic representation of zero and its significance in mathematical contexts.
- - Delve into advanced algebraic concepts, including the role of \( \sqrt{0} \) in algebraic structures.
These resources provide valuable insights and in-depth knowledge to expand your understanding of \( \sqrt{0} \) and its implications across various disciplines.
Xem video để hiểu Square Roots là gì, được giảng dạy bởi Thầy J. Giải thích một cách đơn giản và dễ hiểu về khái niệm này.
Video: Square Roots là gì? | Toán học cùng Thầy J
READ MORE:
Xem video để tìm hiểu về căn bậc hai của số không và các khái niệm liên quan trong toán học.
Video: Căn bậc hai của số không || Toán học một phút || surds