Topic square root of 122: Discover the fascinating properties and calculation methods of the square root of 122. This article delves into its value, rationality, and applications, offering a comprehensive guide to understanding this intriguing mathematical concept. Perfect for students, educators, and math enthusiasts looking to deepen their knowledge.
Table of Content
- Square Root of 122
- Introduction to Square Root of 122
- Value and Properties of Square Root of 122
- Methods to Calculate Square Root of 122
- Prime Factorization Method
- Long Division Method
- Using a Calculator
- Decimal and Exact Form
- Rationality of Square Root of 122
- Applications of Square Root of 122
- Examples of Similar Calculations
- Table of Square Roots Around 122
- Mathematical Representation and Formula
- Conclusion
- YOUTUBE: Khám phá căn bậc hai của 122 với các phương pháp tính toán và ứng dụng thực tế. Video cung cấp kiến thức và ví dụ minh họa chi tiết.
Square Root of 122
The square root of 122 is a mathematical concept that is useful in various fields such as algebra, geometry, and engineering. The square root of a number is a value that, when multiplied by itself, gives the original number.
Value
The square root of 122 is approximately 11.045.
Properties
- Decimal Form: 11.045
- Exact Form: √122
- Rational or Irrational: Irrational
Calculation Methods
-
Prime Factorization
122 can be written as 2 × 61. Since neither 2 nor 61 is a perfect square, the square root of 122 cannot be simplified further using prime factorization.
-
Long Division Method
This method involves a step-by-step process of finding the square root by dividing and averaging. It is useful for manual calculations.
-
Using a Calculator
The most efficient way to find the square root of 122 is by using a calculator, which gives a quick and accurate result of approximately 11.045.
Applications
- Solving quadratic equations
- Geometry problems involving areas and volumes
- Engineering calculations
- Physics problems
Table of Square Roots
| Number | Square Root |
|---|---|
| 121 | 11 |
| 122 | 11.045 |
| 123 | 11.091 |
Mathematical Representation
In mathematical notation, the square root of 122 is represented as:
$$ \sqrt{122} = 11.045 $$
READ MORE:
Introduction to Square Root of 122
The square root of 122 is an interesting mathematical concept that can be expressed in both decimal and radical forms. Understanding the square root of a number involves grasping how it interacts with various mathematical principles and its practical applications.
The square root of 122, denoted as √122, is the value that, when multiplied by itself, equals 122. In decimal form, this value is approximately 11.045. Since 122 is not a perfect square, its square root is an irrational number, meaning it cannot be expressed as a simple fraction.
Here are the main points about the square root of 122:
- Approximate Value: 11.045
- Exact Form: √122
- Type of Number: Irrational
The calculation of the square root of 122 can be approached through various methods, including prime factorization, long division, and using a calculator. Each method offers unique insights into the nature of the square root.
Additionally, the square root of 122 has significant applications in different fields such as geometry, where it might be used to calculate the length of the diagonal of a rectangle or the hypotenuse of a right triangle when combined with the Pythagorean theorem.
Understanding the square root of 122 not only helps in solving specific mathematical problems but also enhances one's overall mathematical intuition and problem-solving skills.
Value and Properties of Square Root of 122
The square root of 122 is approximately 11.045361017187. Since 11.045361017187 is not a whole number, 122 is not a perfect square. The square root of 122 has several important properties and characteristics worth noting.
- Irrational Number: The square root of 122 is an irrational number. This means it cannot be expressed as a simple fraction and its decimal form is non-terminating and non-repeating.
- Calculation: The square root of 122 can be calculated using methods such as the long division method or using a calculator. For example, √122 = 11.045361017187.
- Principal Square Root: The positive square root of 122, known as the principal square root, is 11.045361017187. There is also a negative square root, -11.045361017187, but in most cases, the positive value is used.
- Prime Factorization: The prime factorization of 122 is 2 × 61. Since these prime factors do not pair up, the square root remains irrational.
Table of Roots and Approximations
| Number | Square Root |
| 117 | 10.817 |
| 118 | 10.863 |
| 119 | 10.909 |
| 120 | 10.954 |
| 121 | 11.000 |
| 122 | 11.045361017187 |
| 123 | 11.091 |
| 124 | 11.136 |
| 125 | 11.180 |
| 126 | 11.225 |
The square root of 122 plays a significant role in various mathematical applications and real-world problems, making it a valuable number to understand and utilize.
Methods to Calculate Square Root of 122
The square root of a number can be calculated using several methods, each with its own advantages and steps. Here, we will explore three common methods to find the square root of 122: the long division method, the prime factorization method, and the Newton-Raphson method.
- Long Division Method:
- Start by grouping the digits of 122 from right to left in pairs: (1)(22).
- Find the largest number whose square is less than or equal to the first group. Here, it is 1, since \(1^2 = 1\).
- Subtract the square of this number from the first group and bring down the next group: \(122 - 1 = 121\).
- Double the number found in step 2 (which is 1) and use it as the first digit of the new divisor (making it 2). Find a digit to add to 2 to form a new divisor such that when multiplied by this digit, the product is less than or equal to the new dividend (121). This digit is 5, as \(25 \times 5 = 125\) is close to 121.
- Place the quotient digit next to the first digit, resulting in the approximation of the square root. Here, it is 11.04.
- Prime Factorization Method:
- Factorize 122 into prime factors: \(122 = 2 \times 61\).
- Group the prime factors into pairs. Since there are no pairs of identical factors, the prime factorization method is not suitable for this number.
- Newton-Raphson Method:
- Choose an initial guess, \(x_0\). A reasonable starting point for \(\sqrt{122}\) is 10.
- Apply the iterative formula: \(x_{n+1} = \frac{1}{2} \left( x_n + \frac{122}{x_n} \right)\).
- Repeat the iteration until the value stabilizes. Starting with \(x_0 = 10\):
- \(x_1 = \frac{1}{2} \left( 10 + \frac{122}{10} \right) = 11.1\)
- \(x_2 = \frac{1}{2} \left( 11.1 + \frac{122}{11.1} \right) \approx 11.045\)
- After a few iterations, \(x_n\) will converge to approximately 11.045.
These methods illustrate different approaches to calculating the square root of 122, each suitable for different scenarios depending on the precision required and the tools available.
Prime Factorization Method
Prime factorization is a method used to find the square root of a number by expressing it as the product of its prime factors. Here are the detailed steps to find the square root of 122 using this method:
- Perform Prime Factorization:
Prime factorization involves breaking down the number into its prime factors. For 122, the factorization process is as follows:
- 122 is divisible by 2:
\( 122 \div 2 = 61 \) - 61 is a prime number, so it cannot be factorized further.
Thus, the prime factors of 122 are \(2 \times 61\).
- 122 is divisible by 2:
- Express Using Exponents:
Next, express the prime factors using exponents:
\( 122 = 2^1 \times 61^1 \)
- Calculate the Square Root:
To find the square root, take the square root of each prime factor:
\( \sqrt{122} = \sqrt{2^1 \times 61^1} \)
This simplifies to:
\( \sqrt{122} = \sqrt{2} \times \sqrt{61} \)
Since neither \(\sqrt{2}\) nor \(\sqrt{61}\) are perfect squares, the expression remains in its radical form.
While prime factorization helps in understanding the composition of the number, the square root of 122 is an irrational number and cannot be simplified to an exact decimal. Using a calculator, the approximate value of \(\sqrt{122}\) is 11.045.

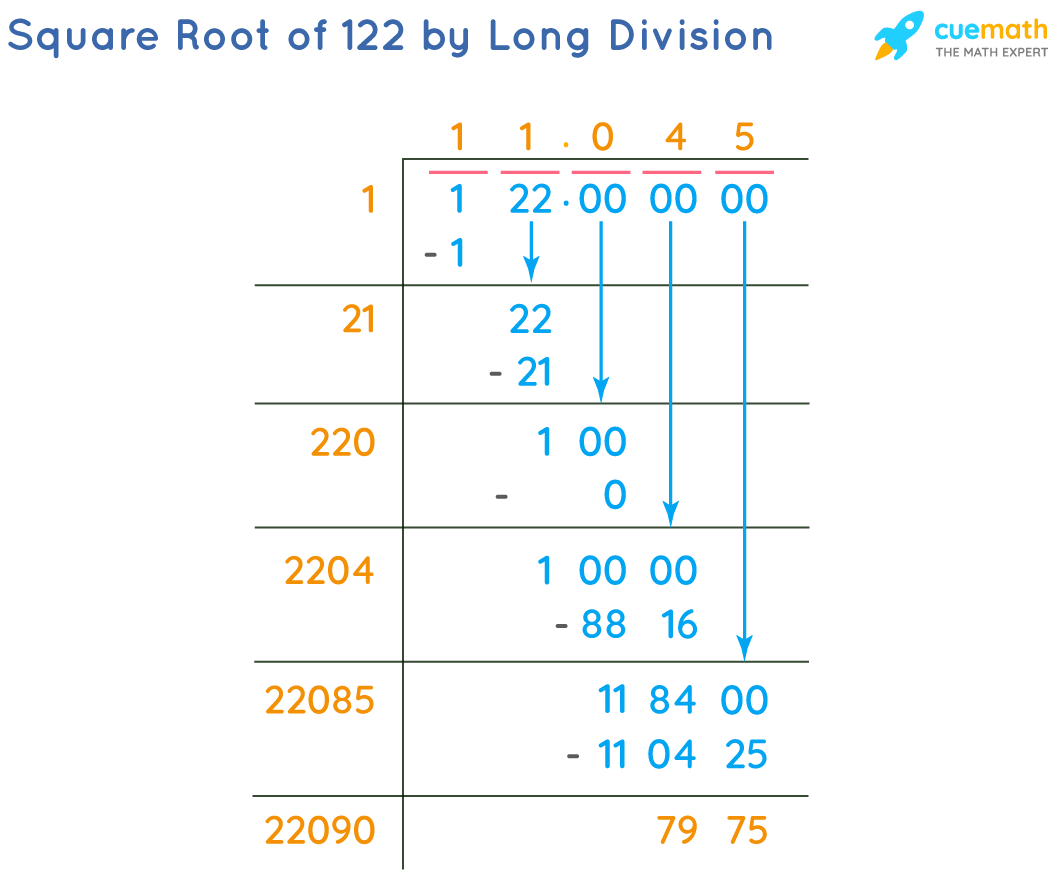
Long Division Method
The long division method is a systematic technique to find the square root of a number. Below are the steps to find the square root of 122 using this method:
- Step 1: Group the digits of 122 in pairs from the decimal point towards the left and right. Here, we consider 122 as 01|22.
- Step 2: Find the largest number whose square is less than or equal to the first group. In this case, 1 squared (1) is the closest.
- Step 3: Subtract the square of this number from the first group and bring down the next pair of digits. This gives 0, and we bring down 22, making it 122.
- Step 4: Double the divisor (1) and enter it with a blank digit on the right. So we write 2_ as the new divisor.
- Step 5: Find a digit to fill in the blank such that when the new divisor is multiplied by this digit, the product is less than or equal to the current dividend. Here, 22 * 5 = 110 is the best choice.
- Step 6: Subtract the product from the current dividend and bring down the next pair of zeros. This gives 122 - 110 = 12, bringing down 00 makes it 1200.
- Step 7: Repeat the process until the desired accuracy is achieved. The next steps continue with 25_, finding the next digit to get closer to the remainder.
The approximate value of the square root of 122 using the long division method is 11.045. This process can be continued to achieve more decimal places of accuracy.
Using a Calculator
Calculating the square root of 122 using a calculator is a straightforward process. Modern calculators, whether basic or scientific, are equipped with a square root function that simplifies this task. Here is a step-by-step guide to help you perform this calculation effectively:
-
Locate the Square Root Button:
- On most calculators, the square root button is represented by the symbol √ or labeled as "sqrt". Ensure you are familiar with its location for quick access.
-
Turn On the Calculator:
- Ensure your calculator is powered on and ready for input. For battery-operated calculators, check that the batteries are functioning correctly.
-
Input the Number:
- Type in the number 122. Make sure you enter the digits accurately to avoid any calculation errors.
-
Press the Square Root Button:
- After entering 122, press the square root (√) button. The calculator will compute the square root and display the result.
-
Read the Result:
- The display should show approximately 11.0454. This is the square root of 122 rounded to four decimal places.
Using a calculator for square root calculations is quick and eliminates the complexity of manual methods. Whether you are using a basic or scientific calculator, these steps ensure you achieve accurate results efficiently.
Decimal and Exact Form
The square root of 122 can be expressed in both its decimal and exact form.
Decimal Form
The decimal form of the square root of 122 is approximately:
\[
\sqrt{122} \approx 11.045361017187261
\]
This value is obtained by calculating the square root to several decimal places, providing a precise approximation.
Exact Form
The exact form of the square root of 122 cannot be simplified into a simpler radical form since 122 is not a perfect square and does not have a square factor other than 1. Hence, it is represented as:
\[
\sqrt{122}
\]
This is the simplest and most exact way to express the square root of 122 without approximation.
Comparison of Forms
| Form | Representation |
|---|---|
| Decimal | 11.045361017187261 |
| Exact | \(\sqrt{122}\) |
Both forms are useful in different contexts. The decimal form is often used in practical calculations where an approximate value is sufficient, while the exact form is preferred in theoretical work and proofs.
Rationality of Square Root of 122
The square root of 122, denoted as \( \sqrt{122} \), is an interesting number when it comes to determining its rationality. In mathematics, a rational number is one that can be expressed as the quotient of two integers, whereas an irrational number cannot be expressed as such a quotient.
To determine whether \( \sqrt{122} \) is rational or irrational, we first consider if 122 is a perfect square. A perfect square is an integer that is the square of another integer. Since there is no integer \( n \) such that \( n^2 = 122 \), we can conclude that 122 is not a perfect square.
Because 122 is not a perfect square, its square root cannot be expressed as a simple fraction, meaning that \( \sqrt{122} \) is an irrational number.
We can further support this by looking at the prime factorization of 122. The prime factorization of 122 is \( 2 \times 61 \). For a number to have a rational square root, all the prime factors must appear in even powers. Since both 2 and 61 are raised to the power of 1, which is odd, \( \sqrt{122} \) is indeed irrational.
To summarize:
- \( 122 \) is not a perfect square.
- The prime factorization \( 2 \times 61 \) has factors raised to an odd power.
- Therefore, \( \sqrt{122} \) is irrational.
Understanding the irrationality of \( \sqrt{122} \) helps in various mathematical contexts, especially in simplifying expressions and solving equations where such roots are involved.
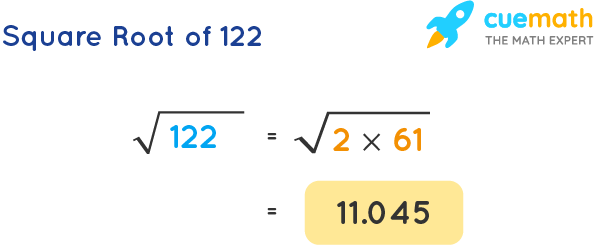
Applications of Square Root of 122
The square root of 122, approximately 11.045, finds applications in various fields, including mathematics, science, engineering, and everyday life. Here are some notable applications:
- Geometry and Trigonometry: Square roots are crucial in solving problems involving right triangles. For instance, using the Pythagorean theorem, you can determine the length of a side in a right triangle when the other two sides are known. In this context, the square root of 122 can represent the length of a side in geometric calculations.
- Physics: In physics, square roots are used to calculate distances, speeds, and other physical properties. For example, calculating the root mean square (RMS) velocity of gas molecules involves square roots, helping to understand kinetic theory and thermodynamics.
- Engineering: Engineers use square roots in various calculations, such as determining the natural frequencies of structures. This helps predict how buildings, bridges, and other structures will respond to environmental forces like wind and earthquakes.
- Statistics: In statistics, square roots are used to compute standard deviation, a measure of the dispersion or variability in a set of data. The standard deviation is the square root of the variance and is essential in data analysis and interpretation.
- Finance: Square roots are used in finance to calculate stock market volatility. The volatility of a stock's returns is often measured as the square root of the variance of the stock's returns, providing insight into the risk and stability of an investment.
- Computer Science: In computer science, square roots are used in algorithms for encryption, image processing, and graphics. For instance, calculating distances in computer graphics often involves the Pythagorean theorem, where the square root is essential.
- Navigation: Navigational calculations often use square roots to determine the shortest path or distance between two points. This is particularly useful in fields such as aviation, marine navigation, and GPS technology.
These examples illustrate the diverse applications of square roots in various disciplines, demonstrating their importance in both theoretical and practical contexts.
Examples of Similar Calculations
Calculating the square root of numbers similar to 122 can be a helpful way to understand the concept and method of finding square roots. Here are some examples of similar calculations:
- Square Root of 23
The square root of 23 is approximately 4.7958.
- Square Root of 26
The square root of 26 is approximately 5.0990.
- Square Root of 42
The square root of 42 is approximately 6.4807.
- Square Root of 56
The square root of 56 is approximately 7.4833.
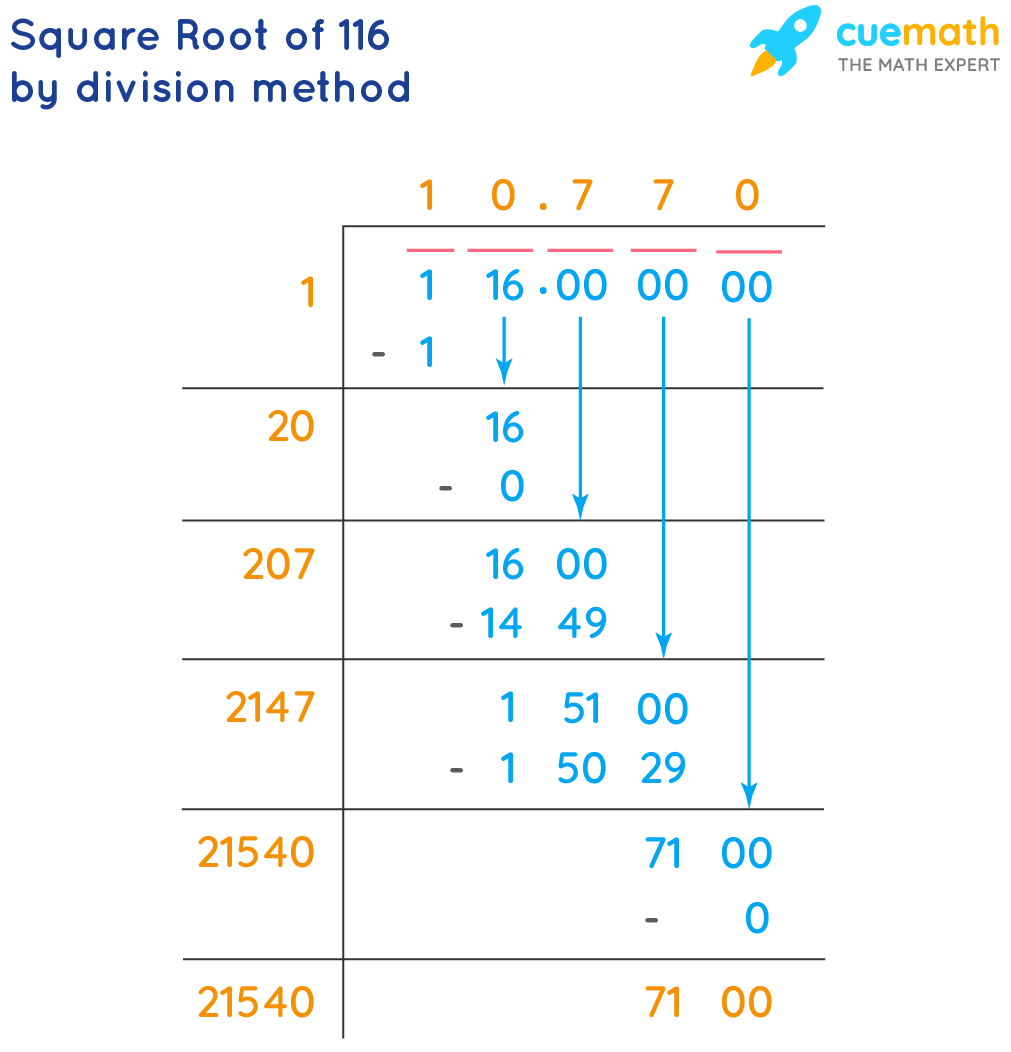
- Square Root of 116
The square root of 116 is approximately 10.7703.
- Square Root of 27
The square root of 27 is approximately 5.1962.
These calculations follow the same principles and methods as finding the square root of 122. Here’s a step-by-step example:
- Long Division Method
To find the square root of 23 using the long division method:
- Set up 23 in pairs: 23.00.
- Find the largest number whose square is less than or equal to 23. Here, it is 4 (since 4² = 16).
- Subtract 16 from 23, giving 7. Bring down the next pair of zeros.
- Double the quotient (4), giving 8. Find a number that, when multiplied by a number close to 80 (like 85), gives a product less than 700. Here, it is 8 (since 85 × 8 = 680).
- Continue this process to find more decimal places if needed.
Thus, the square root of 23 is approximately 4.7958.
- Calculator Method
Using a calculator is straightforward:
- Enter the number (e.g., 26) into the calculator.
- Press the square root (√) button.
- Read the result (approximately 5.0990).
By practicing with these examples, one can become proficient in finding square roots and understanding their properties.
Table of Square Roots Around 122
The following table lists the square roots of numbers around 122, providing both approximate decimal values and simplified radical forms where applicable.
| Number | Square Root (Decimal) | Simplified Radical Form |
|---|---|---|
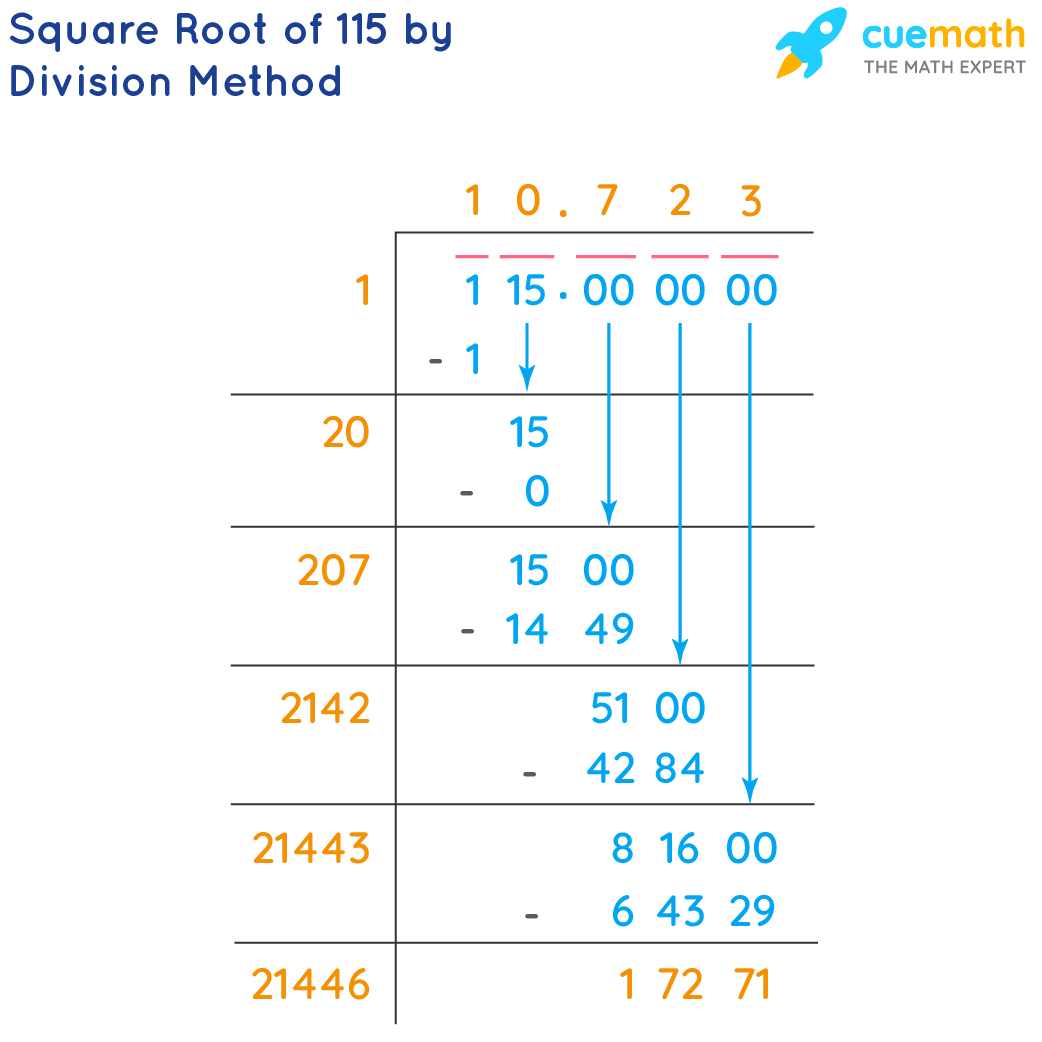
| 115 | 10.7238 | √115 |
| 116 | 10.7703 | √116 |
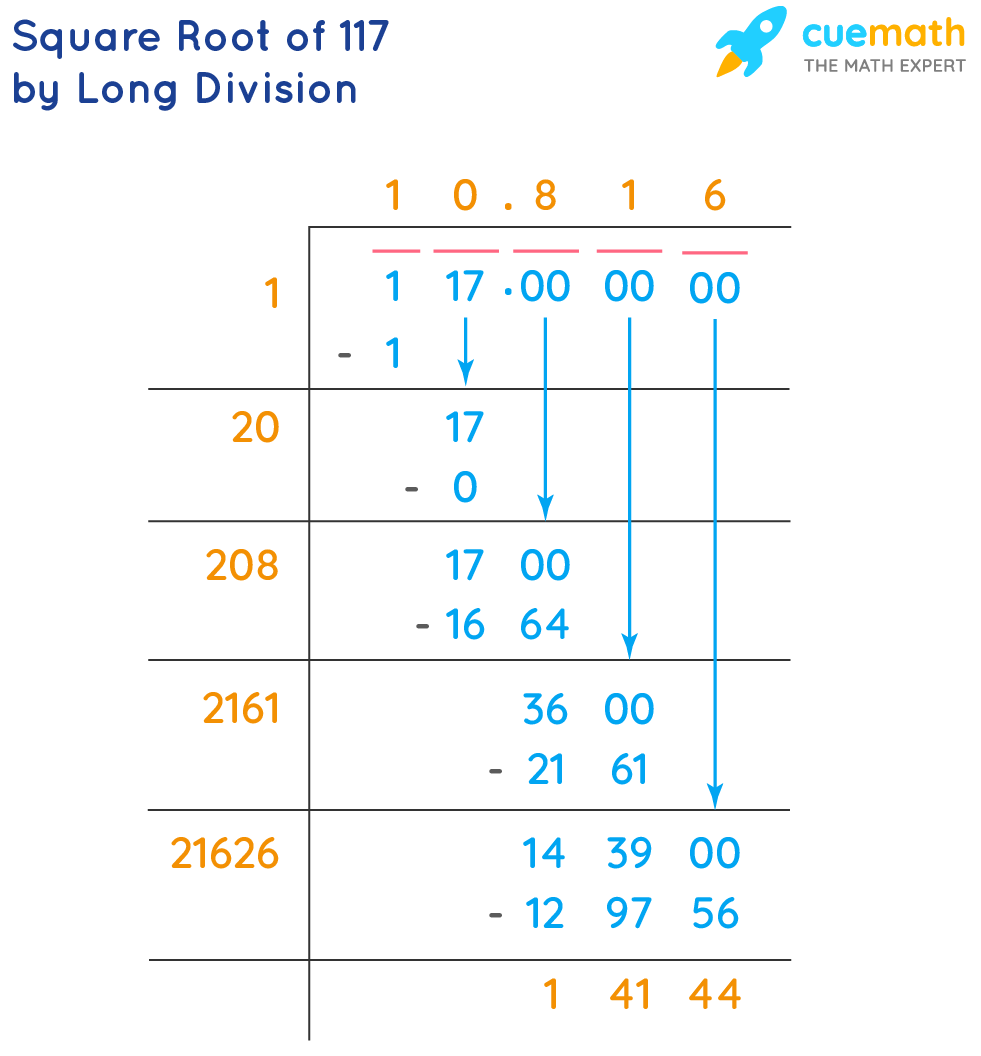
| 117 | 10.8167 | √117 |
| 118 | 10.8628 | √118 |
| 119 | 10.9087 | √119 |
| 120 | 10.9545 | √120 = 2√30 |
| 121 | 11.0000 | 11 |
| 122 | 11.0454 | √122 |
| 123 | 11.0905 | √123 |
| 124 | 11.1355 | √124 = 2√31 |
| 125 | 11.1803 | 5√5 |
| 126 | 11.2249 | √126 = 3√14 |
| 127 | 11.2694 | √127 |
| 128 | 11.3137 | √128 = 8√2 |
| 129 | 11.3578 | √129 |
| 130 | 11.4018 | √130 |
This table can be useful for various mathematical and scientific applications, providing quick reference values for square roots near 122.
Mathematical Representation and Formula
The square root of a number is the value that, when multiplied by itself, gives the original number. The square root is denoted by the radical symbol (√). For any positive number \( x \), the square root can be expressed as:
\[ \sqrt{x} \]
For example, the square root of 122 can be represented as:
\[ \sqrt{122} \]
This can also be written using exponent notation as:
\[ 122^{\frac{1}{2}} \]
Properties of Square Roots
- If \( x \) is a perfect square, then \( \sqrt{x} \) is an integer.
- The square root of a product is the product of the square roots:
- The square root of a quotient is the quotient of the square roots:
- For any non-negative number \( x \), the square root of \( x^2 \) is \( x \):
\[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \]
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
\[ \sqrt{x^2} = x \]
Formula to Find the Square Root
To find the square root of 122 using the long division method, we follow these steps:
- Group the digits of 122 from right to left in pairs: 1 and 22.
- Find the largest number whose square is less than or equal to 1. This number is 1.
- Subtract \( 1^2 \) from 1 to get 0 and bring down the next pair of digits (22), making the new number 22.
- Double the number found in step 2 (1) and write it as 2.
- Find a digit \( x \) such that \( 2x \times x \) is less than or equal to 22. This digit is 4 because \( 24 \times 4 = 96 \leq 122 \).
- The result is approximately 11.045, which is the square root of 122.
Mathematical Representation
The square root of 122 can be expressed in different forms:
- Exact form: \( \sqrt{122} \)
- Decimal form: \( 11.045 \)
Conclusion
The square root of 122 is approximately 11.045, a value that is irrational and non-repeating. Understanding this square root and its properties offers insight into the nature of non-perfect squares and their calculations.
We've explored various methods to calculate the square root of 122, including prime factorization and long division, and we’ve noted its practical applications in fields ranging from engineering to finance. This exploration illustrates the importance of mathematical concepts in both theoretical and practical contexts.
The precise value of the square root of 122 and its properties highlight the beauty of mathematics in solving real-world problems and expanding our understanding of numerical relationships. Whether you're using a calculator or working through manual methods, the process of finding square roots remains a fundamental skill in math education and application.
In summary, the square root of 122 exemplifies how numbers, even those that are not perfect squares, play a crucial role in various disciplines. The study of such numbers not only enhances mathematical knowledge but also reinforces the practical utility of mathematics in everyday life.
Khám phá căn bậc hai của 122 với các phương pháp tính toán và ứng dụng thực tế. Video cung cấp kiến thức và ví dụ minh họa chi tiết.
Căn Bậc Hai của 122
READ MORE:
Khám phá cách tính toán và ứng dụng của căn bậc hai của 122. Video hướng dẫn chi tiết và ví dụ minh họa.
Căn Bậc Hai của 122