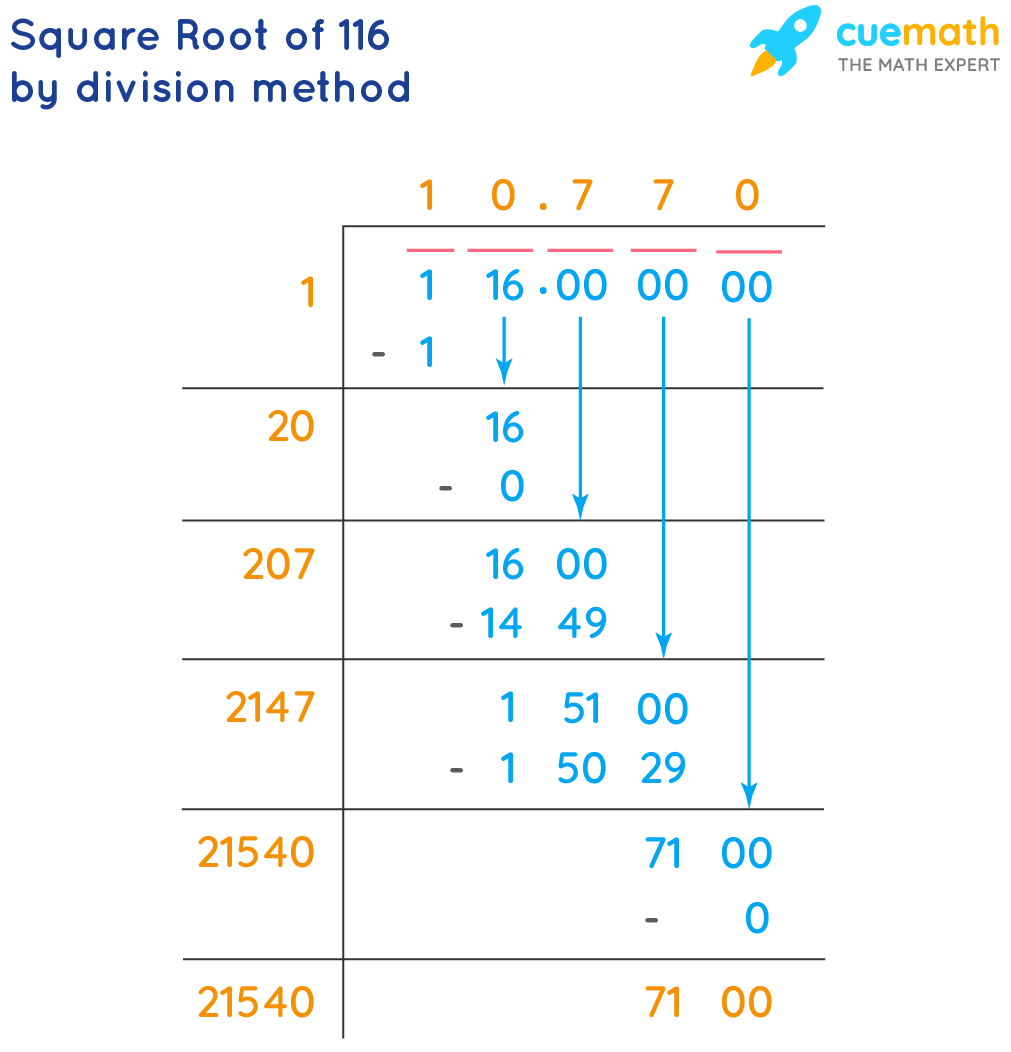
Topic simplify square root of 116: Welcome to our comprehensive guide on how to simplify the square root of 116. Whether you're a student brushing up on your math skills or just curious about the process, this article will break down the steps clearly and concisely. Let's dive into simplifying √116 and making math a bit more approachable!
Table of Content
- Simplifying the Square Root of 116
- Introduction to Simplifying Square Roots
- Steps to Simplify Square Root of 116
- Factoring Method
- Prime Factorization Approach
- Product Rule for Radicals
- Examples and Practice Problems
- Common Questions and Answers
- Applications in Algebra
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai của 116. Tìm hiểu các bước và phương pháp để hiểu rõ hơn về toán học.
Simplifying the Square Root of 116
To simplify the square root of 116, follow these steps:
- Factor 116 into its prime factors: \(116 = 2^2 \times 29\)
- Rewrite the square root of the product: \(\sqrt{116} = \sqrt{2^2 \times 29}\)
- Apply the property of square roots: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- Take the square root of the perfect square: \(\sqrt{2^2} = 2\)
- Combine the results: \(\sqrt{116} = 2\sqrt{29}\)
Exact and Decimal Forms
The simplified form of \(\sqrt{116}\) is \(2\sqrt{29}\). The decimal approximation is:
\(\sqrt{116} \approx 10.7703\)
Visualization
Here is a table summarizing the simplification steps:
| Step | Expression |
|---|---|
| Factor 116 | \(116 = 2^2 \times 29\) |
| Rewrite under the square root | \(\sqrt{116} = \sqrt{2^2 \times 29}\) |
| Apply property | \(\sqrt{2^2 \times 29} = \sqrt{2^2} \times \sqrt{29}\) |
| Take square root of 4 | \(\sqrt{2^2} = 2\) |
| Combine results | \(\sqrt{116} = 2\sqrt{29}\) |

READ MORE:
Introduction to Simplifying Square Roots
Simplifying square roots involves breaking down the number under the radical sign into its prime factors and extracting any perfect squares. This process makes the square root easier to work with and often reveals patterns or simpler forms.
- Start by factoring the number inside the square root. For example, the square root of 116 can be factored into \(2^2 \times 29\).
- Next, use the property that the square root of a product is the product of the square roots. So, \(\sqrt{116} = \sqrt{2^2 \times 29}\).
- Then, simplify by taking the square root of the perfect square factor. Since \(\sqrt{2^2} = 2\), this part comes out from under the radical, leaving us with \(2\sqrt{29}\).
Therefore, the simplified form of \(\sqrt{116}\) is \(2\sqrt{29}\). This method can be applied to any number, making it a valuable tool in algebra and higher-level mathematics.
Steps to Simplify Square Root of 116
Simplifying the square root of 116 involves breaking it down into its simplest radical form. Follow these detailed steps:
-
Factor 116: Identify the factors of 116. The factors are 1, 2, 4, 29, 58, and 116.
-
Find Perfect Squares: From the list of factors, identify the perfect squares. Here, 4 is the only perfect square.
-
Divide by the Largest Perfect Square: Divide 116 by the largest perfect square found. This gives:
\[ 116 \div 4 = 29 \]
-
Square Root of the Perfect Square: Take the square root of 4, which is 2.
\[ \sqrt{4} = 2 \]
-
Combine the Results: Combine the results to express the original square root in its simplest form:
\[ \sqrt{116} = \sqrt{4 \times 29} = \sqrt{4} \times \sqrt{29} = 2 \sqrt{29} \]
Thus, the simplified form of the square root of 116 is \( 2\sqrt{29} \).
This simplification helps in various mathematical calculations and provides a clearer understanding of the number's properties.
Factoring Method
The factoring method involves breaking down the number under the square root into its factors and finding perfect squares among them. Here are the steps to simplify the square root of 116 using the factoring method:
- First, write the number 116 as a product of its prime factors:
\(116 = 2 \times 58 = 2 \times 2 \times 29 = 2^2 \times 29\)
- Identify the perfect square factors:
The perfect square factor here is \(2^2\).
- Rewrite the square root of 116 using the perfect square factor:
\(\sqrt{116} = \sqrt{2^2 \times 29}\)
- Apply the product rule for square roots, which states that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):
\(\sqrt{116} = \sqrt{2^2 \times 29} = \sqrt{2^2} \times \sqrt{29}\)
- Simplify the square root of the perfect square:
\(\sqrt{2^2} = 2\)
- Combine the simplified terms:
\(\sqrt{116} = 2 \times \sqrt{29}\)
Thus, the simplified form of the square root of 116 is:
\(\sqrt{116} = 2\sqrt{29}\)
Prime Factorization Approach
The prime factorization approach involves expressing the number under the square root as a product of its prime factors. Here are the detailed steps to simplify the square root of 116 using this approach:
- First, find the prime factors of 116:
\(116 = 2 \times 58 = 2 \times 2 \times 29 = 2^2 \times 29\)
- Express the square root of 116 in terms of its prime factors:
\(\sqrt{116} = \sqrt{2^2 \times 29}\)
- Apply the property of square roots that states \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):
\(\sqrt{2^2 \times 29} = \sqrt{2^2} \times \sqrt{29}\)
- Simplify the square root of the perfect square factor:
\(\sqrt{2^2} = 2\)
- Combine the simplified terms:
\(\sqrt{116} = 2 \times \sqrt{29}\)
Therefore, the simplified form of the square root of 116 is:
\(\sqrt{116} = 2\sqrt{29}\)
Product Rule for Radicals
The Product Rule for Radicals is a useful property that allows us to simplify the multiplication of square roots. According to this rule, the square root of a product is equal to the product of the square roots of the factors.
The general formula for the Product Rule for Radicals is:
\[\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\]
Let's use this rule to simplify the square root of 116:
- First, identify the factors of 116. We can use the fact that 116 can be factored into 4 and 29, where 4 is a perfect square.
- Write the expression using these factors: \(\sqrt{116} = \sqrt{4 \cdot 29}\).
- Apply the Product Rule for Radicals: \(\sqrt{4 \cdot 29} = \sqrt{4} \cdot \sqrt{29}\).
- Simplify the square roots: \(\sqrt{4} = 2\) and \(\sqrt{29}\) remains as it is because 29 is a prime number and cannot be simplified further.
- Combine the results: \(\sqrt{116} = 2 \cdot \sqrt{29}\).
Thus, using the Product Rule for Radicals, we have simplified \(\sqrt{116}\) to \(2\sqrt{29}\).
Examples and Practice Problems
Understanding how to simplify square roots can be reinforced through examples and practice problems. Below are some examples and practice problems to help you master this concept.
Example 1: Simplify \( \sqrt{72} \)
- Factor \( 72 \) into its prime factors: \( 72 = 2^3 \times 3^2 \).
- Group the prime factors into pairs: \( \sqrt{72} = \sqrt{2^3 \times 3^2} \).
- Take one factor from each pair out of the square root: \( \sqrt{72} = \sqrt{2^2 \times 3^2 \times 2} = 6\sqrt{2} \).
Example 2: Simplify \( \sqrt{108} \)
- Factor \( 108 \) into its prime factors: \( 108 = 2^2 \times 3^3 \).
- Group the prime factors into pairs: \( \sqrt{108} = \sqrt{2^2 \times 3^3} \).
- Take one factor from each pair out of the square root: \( \sqrt{108} = \sqrt{2^2 \times 3^2 \times 3} = 6\sqrt{3} \).
Example 3: Simplify \( \sqrt{50} \)
- Factor \( 50 \) into its prime factors: \( 50 = 2 \times 5^2 \).
- Group the prime factors into pairs: \( \sqrt{50} = \sqrt{2 \times 5^2} \).
- Take one factor from each pair out of the square root: \( \sqrt{50} = \sqrt{5^2 \times 2} = 5\sqrt{2} \).
Practice Problems
- Simplify \( \sqrt{180} \)
- Simplify \( \sqrt{75} \)
- Simplify \( \sqrt{144} \)
- Simplify \( \sqrt{49} \)
Practice Problem Solutions
Here are the solutions to the practice problems:
- \( \sqrt{180} = 6\sqrt{5} \)
- \( \sqrt{75} = 5\sqrt{3} \)
- \( \sqrt{144} = 12 \)
- \( \sqrt{49} = 7 \)
Common Questions and Answers
Understanding the square root of 116 often leads to several common questions. Here, we address some of these questions to aid in comprehension:
Is 116 a perfect square?
No, 116 is not a perfect square. A perfect square is an integer that is the square of another integer. Since 116 cannot be expressed as \( n^2 \) for any integer \( n \), it is not a perfect square.
Is the square root of 116 rational or irrational?
The square root of 116 is an irrational number. Rational numbers can be expressed as a fraction of two integers, whereas irrational numbers cannot be. Since the square root of 116 (approximately 10.77) cannot be written as a precise fraction, it is irrational.
How can the square root of 116 be simplified?
The square root of 116 can be simplified using the prime factorization method:
- Prime factorize 116 to get \( 116 = 2^2 \times 29 \).
- Rewrite the square root as \( \sqrt{116} = \sqrt{2^2 \times 29} \).
- Separate the factors inside the square root using the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Simplify to get \( \sqrt{116} = 2\sqrt{29} \).
What is the exact form of the square root of 116?
The exact form of the square root of 116 is \( 2\sqrt{29} \). This is the simplified radical form.
What is the decimal form of the square root of 116?
The decimal form of the square root of 116 is approximately 10.77. This value is obtained using a calculator.
Can the square root of 116 be expressed as a fraction?
As an irrational number, the square root of 116 cannot be precisely expressed as a fraction. However, it can be approximated. For example, \( \sqrt{116} \approx \frac{1077}{100} \) as a close fractional representation.
What are some practical applications of the square root of 116?
- Geometry and Architecture: Calculating dimensions and areas where precise measurements are crucial.
- Physics and Engineering: Used in formulas involving force, energy, and motion.
- Statistics and Probability: Essential in statistical formulas like standard deviation.
- Art and Design: Used in creating balanced and visually appealing works.
Applications in Algebra
Understanding how to simplify the square root of 116 can be beneficial in various algebraic applications. Here are some key areas where this knowledge is applied:
- Simplifying Expressions: In algebra, you often need to simplify expressions that involve square roots. Knowing that \( \sqrt{116} \) simplifies to \( 2\sqrt{29} \) helps in reducing the complexity of algebraic equations.
- Solving Quadratic Equations: When solving quadratic equations, the square root method is frequently used. For example, if you encounter an equation like \( x^2 = 116 \), you would solve it by taking the square root of both sides, leading to \( x = \pm \sqrt{116} = \pm 2\sqrt{29} \).
- Radical Equations: Simplifying radicals is crucial when working with radical equations. It allows for easier manipulation and solving of equations such as \( \sqrt{116x} = 10 \), which simplifies to \( 2\sqrt{29x} = 10 \), and further to \( \sqrt{29x} = 5 \).
- Geometry and Trigonometry: Simplified square roots are useful in geometric formulas and trigonometric identities. For instance, in the Pythagorean theorem, simplified radicals make it easier to calculate distances and side lengths of right triangles.
- Scientific Notation and Engineering: In fields that use scientific notation, such as physics and engineering, simplified square roots are used for more precise calculations and to avoid errors in measurement.
Practicing the simplification of square roots, such as \( \sqrt{116} \), enhances problem-solving skills and improves overall mathematical proficiency.

Video hướng dẫn cách đơn giản hóa căn bậc hai của 116. Tìm hiểu các bước và phương pháp để hiểu rõ hơn về toán học.
Cách Đơn Giản Hóa Căn Bậc Hai của 116: sqrt(116)
READ MORE:
Video hướng dẫn cách đơn giản hóa căn bậc hai của các số không phải là bình phương hoàn hảo. Tìm hiểu các phương pháp đơn giản hóa căn bậc hai để áp dụng trong toán học.
Cách Đơn Giản Hóa Căn Bậc Hai / Đơn Giản Hóa Căn Bậc Hai của Các Số Không Phải Là Bình Phương Hoàn Hảo