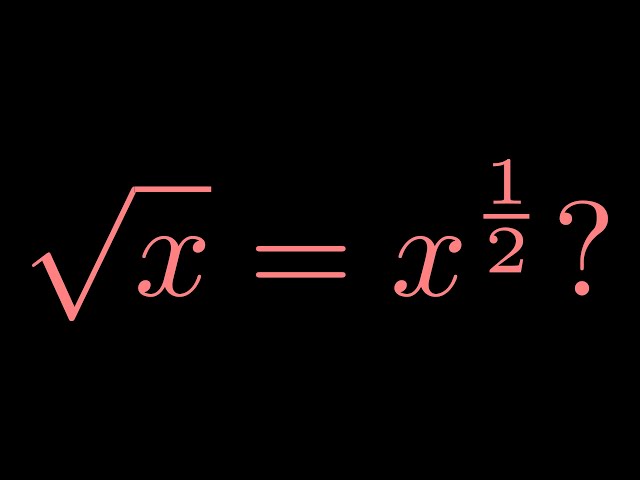Topic square root of 36/169: Unlock the mystery behind calculating the square root of 36/169 with our easy-to-follow guide. Dive into the fundamental concepts, step-by-step solutions, and practical applications that make understanding square roots straightforward and engaging. Perfect for students, educators, and math enthusiasts alike!
Table of Content
- Understanding the Square Root of 36/169
- Introduction to Square Roots
- Understanding Fractions and Their Square Roots
- Calculating the Square Root of 36/169
- Simplifying the Expression
- Visualizing Square Roots
- Applications of Square Roots in Real Life
- Common Mistakes and How to Avoid Them
- Advanced Concepts Related to Square Roots
- Practice Problems and Solutions
- YOUTUBE:
Understanding the Square Root of 36/169
The calculation of the square root of a fraction involves taking the square root of both the numerator and the denominator separately. Here's a detailed explanation of how to find the square root of the fraction 36/169.
Step-by-Step Solution
- Rewrite the fraction as the division of two square roots:
- Simplify the numerator:
- Simplify the denominator:
- Combine the results:
\[
\sqrt{\frac{36}{169}} = \frac{\sqrt{36}}{\sqrt{169}}
\]
\[
\sqrt{36} = 6
\]
\[
\sqrt{169} = 13
\]
\[
\sqrt{\frac{36}{169}} = \frac{6}{13}
\]
Therefore, the square root of the fraction 36/169 is \(\frac{6}{13}\) or approximately 0.4615.
Additional Examples
| Fraction | Square Root |
|---|---|
| 16/81 | \(\frac{4}{9}\) |
| 25/36 | \(\frac{5}{6}\) |
Conclusion
By understanding the method of calculating the square root of both the numerator and the denominator separately, we can easily determine the square root of a fraction. This approach simplifies the process and provides a clear and accurate result.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics that allow us to find a number which, when multiplied by itself, gives the original number. For instance, the square root of 36 is 6 because \(6 \times 6 = 36\).
When dealing with fractions, the process is similar. To find the square root of a fraction, such as \(\frac{36}{169}\), we take the square root of the numerator and the denominator separately.
- Numerator: \( \sqrt{36} = 6 \)
- Denominator: \( \sqrt{169} = 13 \)
Therefore, the square root of \(\frac{36}{169}\) is \(\frac{6}{13}\).
Understanding square roots is crucial in various fields, including algebra, geometry, and real-life applications. By mastering this concept, you can solve complex mathematical problems more efficiently.
Let's explore this concept in detail through step-by-step solutions, practical examples, and visual aids to ensure a comprehensive understanding.
Understanding Fractions and Their Square Roots
Fractions represent parts of a whole and are written as \(\frac{a}{b}\), where \(a\) is the numerator and \(b\) is the denominator. To find the square root of a fraction, you take the square root of both the numerator and the denominator separately.
Let's look at the fraction \(\frac{36}{169}\) as an example:
- Step 1: Identify the numerator and denominator.
- Numerator: 36
- Denominator: 169
- Step 2: Find the square root of the numerator.
- \(\sqrt{36} = 6\)
- Step 3: Find the square root of the denominator.
- \(\sqrt{169} = 13\)
- Step 4: Combine the results to find the square root of the fraction.
- \(\sqrt{\frac{36}{169}} = \frac{6}{13}\)
Thus, the square root of \(\frac{36}{169}\) is \(\frac{6}{13}\). This method can be applied to any fraction, making it a powerful tool for simplifying expressions and solving equations.
By understanding how to work with fractions and their square roots, you can handle more complex mathematical problems with confidence and accuracy.
Calculating the Square Root of 36/169
To calculate the square root of \(\frac{36}{169}\), we will follow a systematic approach by breaking down the problem into smaller, manageable steps.
- Identify the fraction components:
- Numerator: 36
- Denominator: 169
- Calculate the square root of the numerator:
The square root of 36 is found as follows:
- \( \sqrt{36} = 6 \)
- Calculate the square root of the denominator:
The square root of 169 is found as follows:
- \( \sqrt{169} = 13 \)
- Combine the results:
After finding the square roots of both the numerator and the denominator, we combine them to get the square root of the fraction:
- \( \sqrt{\frac{36}{169}} = \frac{\sqrt{36}}{\sqrt{169}} = \frac{6}{13} \)
Thus, the square root of \(\frac{36}{169}\) is \(\frac{6}{13}\). This simple yet effective method can be applied to find the square roots of any fractions, providing a clear and straightforward solution.
By understanding and applying these steps, you can easily calculate the square roots of fractions, enhancing your mathematical skills and problem-solving abilities.
Simplifying the Expression
Simplifying the expression for the square root of a fraction involves breaking it down into simpler parts and ensuring the fraction is in its simplest form. Here, we simplify the expression \(\sqrt{\frac{36}{169}}\).
- Express the square root of the fraction:
- \( \sqrt{\frac{36}{169}} = \frac{\sqrt{36}}{\sqrt{169}} \)
- Calculate the square root of the numerator:
- \( \sqrt{36} = 6 \)
- Calculate the square root of the denominator:
- \( \sqrt{169} = 13 \)
- Combine the simplified parts:
- \( \frac{\sqrt{36}}{\sqrt{169}} = \frac{6}{13} \)
The simplified form of \(\sqrt{\frac{36}{169}}\) is \(\frac{6}{13}\). This method shows that simplifying the square root of a fraction is straightforward when you separately find the square roots of the numerator and the denominator.
By following these steps, you can simplify similar expressions efficiently, making complex calculations easier to manage and understand.

Visualizing Square Roots
Visualizing square roots helps in understanding their magnitude and relation to the numbers involved. Here’s a step-by-step method to visualize the square root of \(\frac{36}{169}\):
- Square Roots on a Number Line:
Place the square roots of whole numbers on a number line for reference:
- \(\sqrt{36} = 6\)
- \(\sqrt{169} = 13\)
This helps in seeing that 6 and 13 are positive numbers lying between 0 and 20 on the number line.
- Comparing the Fraction:
Understand the relationship between the numerator and denominator in terms of square roots:
- \(\sqrt{\frac{36}{169}} = \frac{\sqrt{36}}{\sqrt{169}} = \frac{6}{13}\)
This fraction, \(\frac{6}{13}\), represents a number less than 1 because 6 is less than 13.
- Graphical Representation:
Plot the points on a graph to see the relationship between the square roots:
- Draw a horizontal line for the number line.
- Mark points for 6 and 13.
- Draw vertical lines from these points to represent \(\sqrt{36}\) and \(\sqrt{169}\).
- Comparing Areas:
Visualize squares with sides of length 6 and 13 to compare their areas:
- Area of square with side 6: \(6 \times 6 = 36\)
- Area of square with side 13: \(13 \times 13 = 169\)
This visual comparison shows that the smaller square (side 6) fits within the larger square (side 13), reinforcing that \(\sqrt{36}\) is part of \(\sqrt{169}\).
By visualizing square roots through number lines, graphs, and area comparisons, we gain a better understanding of their values and relationships. This makes it easier to comprehend and work with square roots in mathematical problems.
Applications of Square Roots in Real Life
Square roots have numerous applications in real life, aiding in various fields and everyday scenarios. Here are some practical examples:
- Architecture and Construction:
Square roots are used to calculate dimensions and ensure structures are built correctly. For example, determining the diagonal of a square room helps in planning the layout:
- For a room with sides of 6 meters, the diagonal is \( \sqrt{6^2 + 6^2} = \sqrt{72} = 8.49 \) meters.
- Engineering:
Square roots are essential in engineering calculations, such as stress analysis and material strength. They help in ensuring safety and efficiency:
- Calculating the load a beam can handle involves square root functions to assess stress distribution.
- Physics:
Square roots are fundamental in physics, particularly in wave mechanics and quantum physics:
- Determining the root mean square (RMS) velocity of gas molecules involves square roots.
- Finance:
Square roots are used in financial calculations, such as in determining volatility and risk assessments:
- The standard deviation, which is the square root of variance, measures investment risk.
- Astronomy:
Astronomers use square roots to calculate distances and gravitational forces between celestial bodies:
- Estimating the distance between stars often involves inverse square laws.
- Everyday Problem Solving:
Square roots are useful in various everyday calculations, such as determining areas and volumes:
- Finding the size of a TV screen (diagonal measurement) from its width and height.
Understanding and applying square roots in these real-life situations enhance problem-solving skills and allow for accurate calculations across different domains.
Common Mistakes and How to Avoid Them
When calculating the square root of fractions like \(\frac{36}{169}\), it's important to avoid common mistakes. Here are some pitfalls and tips on how to steer clear of them:
- Not Simplifying the Fraction First:
Before taking the square root, always check if the fraction can be simplified.
- For instance, \(\frac{36}{169}\) is already in its simplest form.
- Incorrectly Applying the Square Root:
Ensure the square root is applied to both the numerator and the denominator separately:
- Correct: \( \sqrt{\frac{36}{169}} = \frac{\sqrt{36}}{\sqrt{169}} = \frac{6}{13} \)
- Incorrect: \( \sqrt{\frac{36}{169}} = \sqrt{\frac{6}{13}} \)
- Forgetting to Simplify Results:
After finding the square roots, simplify the result if possible:
- For \(\sqrt{\frac{36}{169}}\), \(\frac{6}{13}\) is already simplified.
- Misplacing the Square Root Symbol:
Ensure the square root symbol is correctly placed to avoid confusion:
- Correct: \( \sqrt{\frac{36}{169}} \)
- Incorrect: \( \frac{\sqrt{36}}{169} \)
- Ignoring Negative Roots:
Remember that square roots can be both positive and negative, but in most cases, we consider the principal (positive) root:
- Principal root: \( \sqrt{36} = 6 \)
- Negative root: \( -\sqrt{36} = -6 \)
- Incorrect Fractional Calculations:
Ensure the fractions are correctly calculated when combining square roots:
- Check intermediate steps to avoid calculation errors.
By being aware of these common mistakes and following these tips, you can accurately calculate the square roots of fractions and enhance your mathematical proficiency.
Advanced Concepts Related to Square Roots
The concept of square roots extends beyond the basic calculation and has several advanced aspects that are fundamental in higher mathematics. Below, we will explore some of these advanced concepts related to square roots.
1. Rational and Irrational Square Roots
Square roots can be classified as rational or irrational numbers. A rational square root is a number that can be expressed as the quotient of two integers, whereas an irrational square root cannot be expressed as such. For example:
- The square root of 36/169 is a rational number because both 36 and 169 are perfect squares, and their square roots (6 and 13) are integers. Thus, √(36/169) = 6/13.
- The square root of 2 is an irrational number because it cannot be expressed as a ratio of two integers.
2. Simplification of Square Roots
Simplifying square roots involves expressing the root in its simplest form. This is particularly useful when dealing with algebraic expressions and equations. For instance, the square root of a fraction can be simplified as follows:
- Separate the numerator and the denominator: √(a/b) = √a / √b
- Simplify each part if possible: for √(36/169), √36 = 6 and √169 = 13, so √(36/169) = 6/13
3. Properties of Square Roots
Understanding the properties of square roots is essential for solving more complex mathematical problems. Some key properties include:
- Product Property: √(a * b) = √a * √b
- Quotient Property: √(a / b) = √a / √b
- Powers of Square Roots: (√a)^2 = a
4. Complex Numbers and Square Roots
When dealing with negative numbers, square roots lead to complex numbers. The square root of a negative number is expressed using the imaginary unit 'i', where i = √(-1). For example:
- √(-4) = 2i
- √(-9) = 3i
5. Square Roots in Algebraic Equations
Square roots frequently appear in algebraic equations. Solving these equations often involves isolating the square root term and then squaring both sides of the equation to eliminate the root. For example:
Solve for x in the equation √(x + 3) = 5:
- Square both sides: (√(x + 3))^2 = 5^2
- Which simplifies to: x + 3 = 25
- Subtract 3 from both sides: x = 22
6. The Binomial Theorem and Square Roots
The Binomial Theorem can be applied to expressions involving square roots to expand them. This is particularly useful in calculus and series expansions. For instance:
The expansion of (a + b)^(1/2) using the Binomial Theorem is:
- (a + b)^(1/2) = 1 + (1/2)a + (1/2)(-1/2)(a^2)/2! + ...
7. Square Roots and Differential Equations
Square roots also appear in solutions to certain types of differential equations. For example, the solution to a simple harmonic oscillator can involve square root functions.
For a differential equation of the form: d^2x/dt^2 + ω^2x = 0, the general solution is:
- x(t) = A cos(ωt) + B sin(ωt), where ω is a constant involving a square root.
Understanding these advanced concepts related to square roots provides a deeper insight into their applications in various fields of mathematics and science.

Practice Problems and Solutions
Practice problems help reinforce the concepts related to the square root of fractions. Here are several problems along with their solutions to help you understand and master these concepts.
Problem 1: Simplifying the Square Root of a Fraction
Simplify the expression: \( \sqrt{\frac{36}{169}} \)
Solution:
- Rewrite the square root of the fraction as the fraction of the square roots: \( \sqrt{\frac{36}{169}} = \frac{\sqrt{36}}{\sqrt{169}} \)
- Calculate the square root of the numerator and the denominator separately:
- \( \sqrt{36} = 6 \)
- \( \sqrt{169} = 13 \)
- Combine the results: \( \frac{\sqrt{36}}{\sqrt{169}} = \frac{6}{13} \)
Thus, \( \sqrt{\frac{36}{169}} = \frac{6}{13} \).
Problem 2: Simplifying Complex Fractions
Simplify the expression: \( \sqrt{\frac{25}{144}} \)
Solution:
- Rewrite the square root of the fraction as the fraction of the square roots: \( \sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}} \)
- Calculate the square root of the numerator and the denominator separately:
- \( \sqrt{25} = 5 \)
- \( \sqrt{144} = 12 \)
- Combine the results: \( \frac{\sqrt{25}}{\sqrt{144}} = \frac{5}{12} \)
Thus, \( \sqrt{\frac{25}{144}} = \frac{5}{12} \).
Problem 3: Applying the Concept to a Real-World Problem
If the area of a rectangle is represented by the fraction \( \frac{36}{169} \) square units, what is the side length of the rectangle if it is a square?
Solution:
- Since the rectangle is a square, all sides are equal. The area \( A \) of a square is given by \( A = s^2 \), where \( s \) is the side length.
- Set up the equation \( s^2 = \frac{36}{169} \).
- To find \( s \), take the square root of both sides: \( s = \sqrt{\frac{36}{169}} \).
- Using the previous results: \( s = \frac{6}{13} \).
Thus, the side length of the square is \( \frac{6}{13} \) units.
Problem 4: More Practice with Different Fractions
Simplify the expression: \( \sqrt{\frac{49}{196}} \)
Solution:
- Rewrite the square root of the fraction as the fraction of the square roots: \( \sqrt{\frac{49}{196}} = \frac{\sqrt{49}}{\sqrt{196}} \).
- Calculate the square root of the numerator and the denominator separately:
- \( \sqrt{49} = 7 \)
- \{ \sqrt{196} = 14 \}
- Combine the results: \( \frac{\sqrt{49}}{\sqrt{196}} = \frac{7}{14} \).
- Simplify the fraction: \( \frac{7}{14} = \frac{1}{2} \).
Thus, \( \sqrt{\frac{49}{196}} = \frac{1}{2} \).
Problem 5: Comparing Square Roots of Fractions
Compare \( \sqrt{\frac{36}{169}} \) and \( \sqrt{\frac{25}{144}} \).
Solution:
- We have already calculated \( \sqrt{\frac{36}{169}} = \frac{6}{13} \) and \( \sqrt{\frac{25}{144}} = \frac{5}{12} \).
- To compare, find a common denominator:
- Convert \( \frac{6}{13} \) and \( \frac{5}{12} \) to have the same denominator (common denominator = 156).
- \( \frac{6}{13} = \frac{6 \times 12}{13 \times 12} = \frac{72}{156} \).
- \( \frac{5}{12} = \frac{5 \times 13}{12 \times 13} = \frac{65}{156} \).
- Compare the numerators: \( 72 > 65 \), so \( \frac{6}{13} > \frac{5}{12} \).
Thus, \( \sqrt{\frac{36}{169}} \) is greater than \( \sqrt{\frac{25}{144}} \).
Square Root 169
READ MORE:
Cách đơn giản hóa phân số trong căn bậc hai: √(121/169)