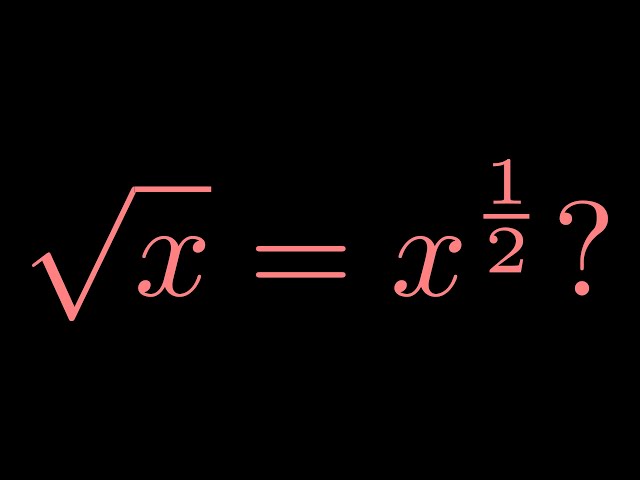Topic square root of 115: Discover the fascinating world of the square root of 115. This article explores its mathematical significance, methods of calculation, and real-life applications. Whether you're a student, educator, or math enthusiast, you'll find valuable insights and practical knowledge about this intriguing number. Dive in to enhance your understanding and appreciation of the square root of 115.
Table of Content
- Square Root of 115
- Introduction
- What is the Square Root of 115?
- Mathematical Definition and Properties
- Decimal and Fractional Representation
- Methods to Calculate the Square Root
- Long Division Method
- Calculator Method
- Estimation and Approximation Techniques
- Real-life Applications of Square Roots
- Understanding Irrational Numbers
- Comparison with Other Square Roots
- Historical Context and Usage
- YOUTUBE:
Square Root of 115
The square root of 115 is a number that, when multiplied by itself, gives the result of 115. It is represented as \( \sqrt{115} \).
Exact Value
The square root of 115 cannot be expressed as an exact integer or a simple fraction, as 115 is not a perfect square. Therefore, it is an irrational number. The square root of 115 is approximately:
\[
\sqrt{115} \approx 10.723805
\]
Decimal Form
When expressed in decimal form, the square root of 115 is approximately:
\[
10.723805294763608
\]
Properties
- Square: \( \sqrt{115} \times \sqrt{115} = 115 \)
- Square Root of 115 in Simplest Radical Form: The simplest form is \( \sqrt{115} \) as it cannot be simplified further.
- Decimal Approximation: The value is approximately 10.723805.
- Nature of the Number: It is an irrational number since it cannot be expressed as a simple fraction.
Calculation Method
To calculate the square root of 115, you can use various methods such as:
- Long Division Method: A manual method to find the square root which involves division and averaging.
- Using a Calculator: The most straightforward way is to use a scientific calculator.
- Estimation Method: Estimating by finding the nearest perfect squares. For example, \( \sqrt{100} = 10 \) and \( \sqrt{121} = 11 \), so \( \sqrt{115} \) is between 10 and 11.
Conclusion
Understanding the square root of 115 helps in various mathematical and real-world applications. Whether using it in calculations, solving equations, or understanding its properties, it is a fundamental concept in mathematics.
READ MORE:
Introduction
The square root of 115 is a captivating mathematical concept that often intrigues students and enthusiasts alike. Represented as \( \sqrt{115} \), it signifies a value that, when multiplied by itself, equals 115. This number is not a perfect square, making its square root an irrational number. In this section, we will explore its definition, properties, and various methods of calculation in a detailed, step-by-step manner.
- Definition: The square root of a number is a value that, when multiplied by itself, gives the original number. For 115, this is represented as \( \sqrt{115} \).
- Properties: Since 115 is not a perfect square, its square root is an irrational number, meaning it cannot be expressed as a simple fraction and has an infinite, non-repeating decimal expansion.
- Methods of Calculation:
- Long Division Method: A manual technique to find the square root by dividing and averaging.
- Calculator Method: Using a scientific calculator for a quick and accurate result.
- Estimation and Approximation: Estimating the value by finding the nearest perfect squares, such as \( \sqrt{100} = 10 \) and \( \sqrt{121} = 11 \), and determining that \( \sqrt{115} \) lies between 10 and 11.
Understanding the square root of 115 involves not just finding its numerical value but also appreciating its place in mathematics and its practical applications in various fields. Let's delve deeper into each aspect to gain a comprehensive understanding of this intriguing number.
What is the Square Root of 115?
The square root of 115, represented as \( \sqrt{115} \), is a number that, when multiplied by itself, equals 115. Since 115 is not a perfect square, its square root is an irrational number. This means that it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion. The approximate value of \( \sqrt{115} \) is:
\[
\sqrt{115} \approx 10.723805
\]
- Exact Value: As an irrational number, the exact value of the square root of 115 cannot be precisely written in decimal form.
- Decimal Form: The decimal representation of \( \sqrt{115} \) is approximately 10.723805294763608, which can be rounded to 10.724 for simplicity in most practical uses.
Calculation Methods
- Long Division Method:
This manual method involves dividing and averaging to get closer to the square root value step by step. It is labor-intensive but can yield a precise result with enough iterations.
- Calculator Method:
Using a scientific calculator is the quickest way to find the square root of 115. Simply input the number and press the square root function to get an accurate result.
- Estimation and Approximation:
By identifying the nearest perfect squares, 100 (\( \sqrt{100} = 10 \)) and 121 (\( \sqrt{121} = 11 \)), we can estimate that \( \sqrt{115} \) lies between 10 and 11. Refining this estimate, we find that it is approximately 10.724.
Properties of the Square Root of 115
- Irrational Nature: As mentioned, \( \sqrt{115} \) is irrational, meaning it cannot be expressed as a simple fraction.
- Non-repeating Decimal: Its decimal form extends infinitely without repeating, which is a characteristic of irrational numbers.
Understanding the square root of 115 involves both recognizing its mathematical properties and knowing how to calculate it using various methods. This fundamental concept is not only important in pure mathematics but also has practical applications in science, engineering, and everyday problem-solving.
Mathematical Definition and Properties
The square root of a number is a value that, when multiplied by itself, gives the original number. For 115, this is represented as \( \sqrt{115} \). Since 115 is not a perfect square, its square root is an irrational number. Here, we delve into the mathematical definition and properties of the square root of 115.
Mathematical Definition
- Square Root: The square root of 115 is the number that satisfies the equation: \[ x^2 = 115 \] This number is denoted as \( \sqrt{115} \).
- Irrational Number: Because 115 is not a perfect square, \( \sqrt{115} \) cannot be expressed as a simple fraction, and its decimal representation is non-terminating and non-repeating.
Properties
- Decimal Representation: The approximate decimal value of \( \sqrt{115} \) is 10.723805294763608, which is often rounded to 10.724 for simplicity.
- Non-repeating Decimal: As an irrational number, the decimal form of \( \sqrt{115} \) extends infinitely without repeating.
- Positive and Negative Roots: Mathematically, both \( \sqrt{115} \) and \( -\sqrt{115} \) are solutions to the equation \( x^2 = 115 \). However, the principal square root is taken to be the positive value, 10.724.
Prime Factorization
To understand why 115 is not a perfect square, we can look at its prime factorization:
\[
115 = 5 \times 23
\]
Since neither 5 nor 23 is a perfect square, 115 itself cannot be a perfect square.
Approximation Methods
- Nearest Perfect Squares: Identifying the perfect squares closest to 115 (namely, 100 and 121) helps to estimate that \( \sqrt{115} \) is between 10 and 11.
- Refinement: By further narrowing down, it is determined that \( \sqrt{115} \) is approximately 10.724.
Applications
- Science and Engineering: The square root of 115 can be used in various calculations in physics, engineering, and other sciences where precise measurements are necessary.
- Mathematical Problems: Understanding the properties of \( \sqrt{115} \) can help in solving algebraic equations and other mathematical problems.
In summary, the square root of 115 is an irrational number with a non-repeating, non-terminating decimal expansion. It is important in various fields of study and practical applications, making it a significant concept in mathematics.
Decimal and Fractional Representation
The square root of 115, \( \sqrt{115} \), is an important number in mathematics with both decimal and fractional representations. Although it is an irrational number, its approximate values can be expressed in different ways for practical purposes.
Decimal Representation
- Exact Decimal Form: The exact value of \( \sqrt{115} \) is a non-repeating, non-terminating decimal. Its approximate value is: \[ \sqrt{115} \approx 10.723805294763608 \]
- Rounded Decimal Form: For simplicity and ease of use in calculations, \( \sqrt{115} \) is often rounded to a more manageable decimal value, such as 10.724.
Fractional Representation
- Approximating with Fractions: While \( \sqrt{115} \) cannot be precisely expressed as a fraction, it can be approximated using rational numbers. One common method is to find two close fractions that approximate the decimal value. For instance: \[ 10.723805 \approx \frac{10724}{1000} \] This fraction can be simplified further if needed.
- Continued Fraction: Another method to represent \( \sqrt{115} \) is through continued fractions, which provide a sequence of fractions that increasingly approximate the square root. The continued fraction for \( \sqrt{115} \) starts as follows: \[ \sqrt{115} \approx 10 + \frac{1}{7 + \frac{1}{2 + \frac{1}{1 + \cdots}}} \]
Steps to Find Decimal Representation
- Identify Nearest Perfect Squares: Determine the perfect squares closest to 115, such as 100 (\( \sqrt{100} = 10 \)) and 121 (\( \sqrt{121} = 11 \)), to estimate that \( \sqrt{115} \) is between 10 and 11.
- Use a Calculator: For a precise value, use a scientific calculator to find that \( \sqrt{115} \approx 10.723805 \).
- Long Division Method: Manually compute the square root by iteratively dividing and averaging, which can yield the decimal representation to desired precision.
Understanding the decimal and fractional representations of \( \sqrt{115} \) provides a clearer insight into its nature as an irrational number. These approximations are useful in various mathematical calculations and practical applications, making them an essential part of mathematical studies.

Methods to Calculate the Square Root
Calculating the square root of a number, such as 115, can be approached through various methods. Here, we explore different techniques that can be used to find the square root of 115, ranging from manual calculations to using technological tools.
1. Long Division Method
The long division method is a manual process that involves dividing and averaging to find the square root. This method is precise and can be used to find square roots to several decimal places.
- Set Up the Division: Write the number 115 under the long division symbol.
- Group the Digits: Starting from the decimal point, group the digits of the number in pairs, adding zeros if necessary.
- Find the Largest Square: Find the largest number whose square is less than or equal to the first group. In this case, the first group is 1, and the largest square is 1 (since \(1^2 = 1\)).
- Subtract and Bring Down: Subtract the square from the first group and bring down the next pair of digits. Continue this process iteratively.
- Average the Quotients: Continue the process of dividing and averaging to refine the value of the square root.
2. Calculator Method
The calculator method is the quickest and easiest way to find the square root of 115. Using a scientific calculator, simply input the number 115 and press the square root button (√). The calculator will display the approximate value:
\[
\sqrt{115} \approx 10.723805
\]
3. Estimation and Approximation
Estimating the square root involves identifying the nearest perfect squares and refining the estimate through approximation techniques.
- Identify Nearest Perfect Squares: The perfect squares closest to 115 are 100 (\( \sqrt{100} = 10 \)) and 121 (\( \sqrt{121} = 11 \)). Thus, \( \sqrt{115} \) lies between 10 and 11.
- Refine the Estimate: By using a process of trial and error or averaging, further narrow down the value: \[ 10.7^2 = 114.49 \quad \text{and} \quad 10.8^2 = 116.64 \] Since 114.49 is closer to 115, we can further refine to \( 10.72 \) and so on until we get a satisfactory approximation.
4. Newton's Method (Iterative Approximation)
Newton's method, also known as the Newton-Raphson method, is an iterative numerical technique used to find successively better approximations to the roots (or zeroes) of a real-valued function.
- Initial Guess: Start with an initial guess, \( x_0 \). For \( \sqrt{115} \), a good starting point is 10.7.
- Iterative Formula: Use the iterative formula: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{115}{x_n} \right) \]
- Repeat the Process: Continue the iteration until the change between successive approximations is smaller than the desired level of precision.
By using these methods, one can accurately determine the square root of 115, each method offering different levels of precision and complexity. Whether through manual calculation or using a calculator, understanding these techniques is essential for various mathematical applications.
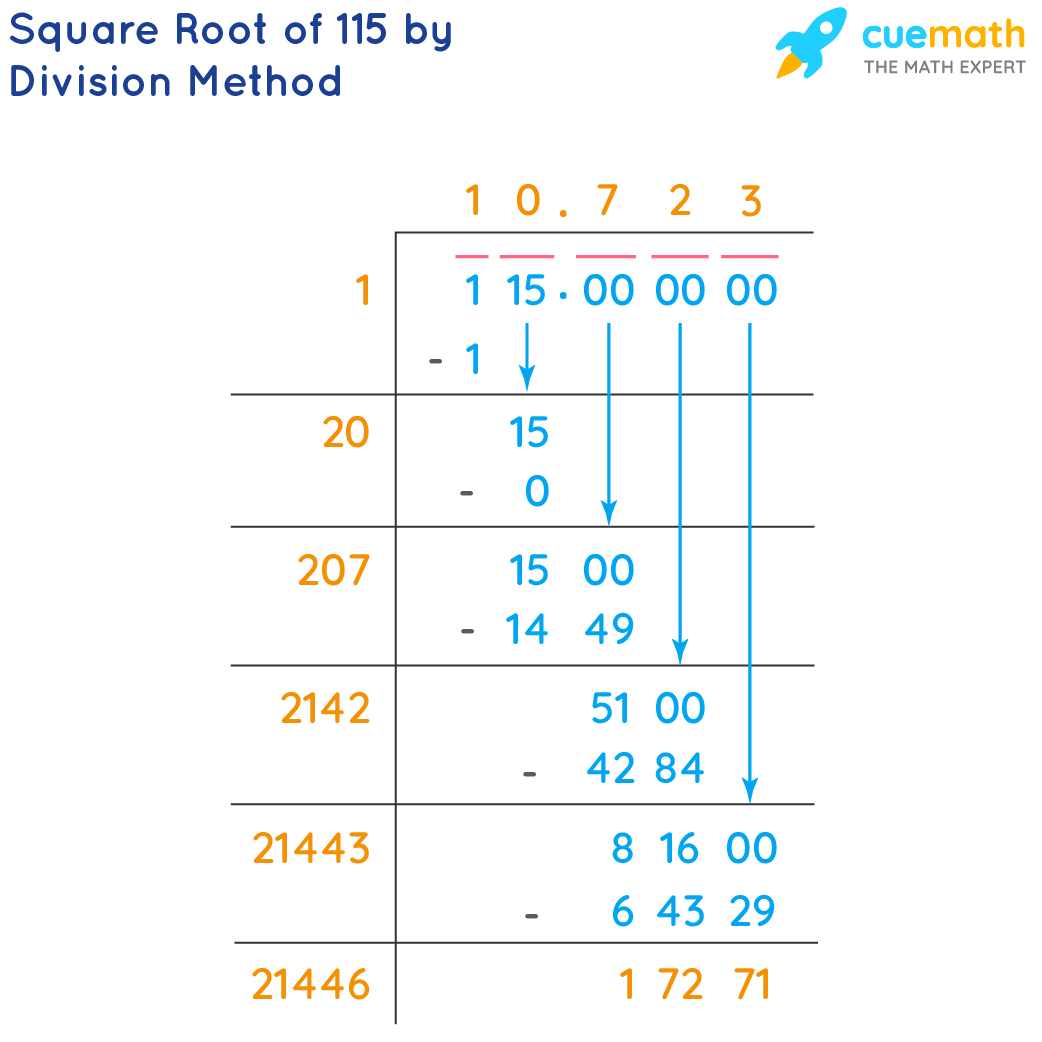
Long Division Method
The long division method is a traditional and manual technique used to find the square root of a number, such as 115. This method involves a series of steps that allow for an accurate calculation of the square root to several decimal places. Below is a detailed, step-by-step guide to using the long division method to calculate \( \sqrt{115} \).
- Set Up the Division: Write 115 as the number to be divided under the long division symbol.
- Group the Digits: Starting from the decimal point, group the digits of 115 in pairs. If there are not enough digits, add zeros. For 115, the pairs are (1, 15).
- Find the Largest Square: Find the largest number whose square is less than or equal to the first group (1 in this case). This number is 1, since \(1^2 = 1\). Write 1 as the first digit of the square root and subtract 1 from the first group, bringing down the next pair of digits to get 15.
- Double the Quotient: Double the current quotient (1) to get 2, and write it as the first part of the new divisor.
- Determine the Next Digit: Find a digit (x) such that when the new divisor (20 + x) is multiplied by x, the product is less than or equal to the current dividend (15). In this case, 0 works since \(20 \times 0 = 0\). Write 0 as the next digit of the quotient.
- Bring Down the Next Pair: Subtract the product (0) from the current dividend (15) to get 15, then bring down the next pair of digits (00) to make 1500.
- Repeat the Process: Continue the process by doubling the current quotient (10) to get 20, and repeat the steps. Find a digit (7) such that when 207 is multiplied by 7, the product (1449) is less than or equal to 1500. Subtract to get 51, bring down the next pair (00) to make 5100.
- Continue the Iteration: Repeat these steps to further refine the value:
- Double the quotient (107) to get 214, find 2 such that 2142 * 2 is less than or equal to 5100, write 2.
- Continue subtracting and bringing down pairs of zeros, repeating the steps to increase the precision of the square root calculation.
After a sufficient number of iterations, the square root of 115 can be approximated to the desired decimal places. For example, after a few iterations, you get:
\[
\sqrt{115} \approx 10.723
\]
Using the long division method, you can obtain a precise value of the square root by following these detailed steps. This traditional technique is an excellent way to understand the process of finding square roots manually.
Calculator Method
The calculator method is one of the most efficient and straightforward ways to find the square root of a number, such as 115. This method involves using a scientific calculator to quickly and accurately determine the square root. Below are the detailed steps to find the square root of 115 using a calculator.
- Turn on the Calculator: Ensure your calculator is turned on and in the correct mode for performing square root calculations. Most scientific calculators have a dedicated square root function, often denoted by the symbol √.
- Enter the Number: Input the number 115 into the calculator. This is done by pressing the respective keys for 1, 1, and 5.
- Press the Square Root Button: Locate and press the square root button (√) on your calculator. This button may be directly accessible or may require pressing a secondary function key (usually labeled as "2nd" or "shift") before pressing the √ button.
- Read the Result: The calculator will display the square root of 115. The display should show the approximate value:
\[
\sqrt{115} \approx 10.723805
\]
Advantages of Using a Calculator
- Speed: Calculators provide an instantaneous result, making them the fastest method for finding square roots.
- Accuracy: Scientific calculators are designed to handle complex mathematical functions accurately, ensuring a precise result.
- Convenience: Using a calculator is straightforward and requires minimal effort, making it an accessible tool for students, professionals, and anyone needing quick calculations.
Example Calculation
Let's walk through an example of finding the square root of 115 using a calculator:
- Turn on the calculator and clear any previous entries.
- Enter the number 115 by pressing the keys: 1, 1, 5.
- Press the square root button (√). On some calculators, this may involve pressing the "2nd" or "shift" key followed by the √ button.
- The display will show the result: 10.723805294763608. This can be rounded to 10.724 for simplicity in most practical applications.
By following these simple steps, you can efficiently use a calculator to find the square root of 115. This method is highly reliable and is a valuable tool in both educational and professional settings.
Estimation and Approximation Techniques
Estimating and approximating the square root of 115 can be approached using various methods. Below are some common techniques:
Using Perfect Squares
One way to estimate the square root is by finding the nearest perfect squares. We know that:
- \(\sqrt{100} = 10\)
- \(\sqrt{121} = 11\)
Since 115 is between 100 and 121, we can conclude that:
\(10 < \sqrt{115} < 11\)
Linear Interpolation
We can use linear interpolation between the square roots of 100 and 121 to get a closer estimate:
Let's assume the relationship is approximately linear:
\(\sqrt{115} \approx 10 + \frac{115 - 100}{121 - 100}\)
Calculating the above:
\(\sqrt{115} \approx 10 + \frac{15}{21} \approx 10 + 0.714 \approx 10.714\)
Newton's Method
Newton's Method (also known as the Newton-Raphson method) is an iterative technique to approximate the square root:
- Start with an initial guess \(x_0\). Let's use \(x_0 = 10.5\) as our initial guess.
- Use the formula \(x_{n+1} = \frac{1}{2} \left( x_n + \frac{115}{x_n} \right)\).
- Repeat the iteration until the value stabilizes.
Let's perform a few iterations:
\(x_1 = \frac{1}{2} \left( 10.5 + \frac{115}{10.5} \right) \approx 10.7357\)
\(x_2 = \frac{1}{2} \left( 10.7357 + \frac{115}{10.7357} \right) \approx 10.7238\)
After a few more iterations, the value converges to approximately \(10.7238\).
Using a Number Line
An intuitive way to estimate is by plotting on a number line:
| 10 | | | 10.5 | | | 11 |
We can place 115 closer to 121, so visually the square root of 115 is closer to 10.7 than to 10.5 or 11.
Comparison with Calculator Value
Using a calculator, we find:
\(\sqrt{115} \approx 10.7238\)
This matches closely with our approximations using Newton's Method and other techniques.

Real-life Applications of Square Roots
Square roots have a wide range of applications in various fields. Here are some notable real-life examples:
-
Geometry and Construction:
Square roots are essential in geometry, particularly in the Pythagorean theorem, which is used to calculate distances and measurements in construction and carpentry. For example, if you know the lengths of two sides of a right triangle, you can use the square root to find the length of the hypotenuse:
\[
c = \sqrt{a^2 + b^2}
\] -
Physics:
Square roots are used in various physics formulas, such as calculating the period of a pendulum or the speed of an object in free fall. For instance, the time it takes for an object to fall from a height \( h \) is given by:
\[
t = \frac{\sqrt{h}}{4}
\] -
Finance:
In finance, square roots are used to calculate the volatility of stock prices and to determine compound interest rates over multiple periods. The formula for the annualized return over two periods is:
\[
R = \sqrt{\frac{V_2}{V_0}} - 1
\] -
Statistics and Probability:
Square roots are crucial in statistics, especially in the calculation of standard deviations and variances. These measures help in understanding the spread of data points in a dataset. The formula for the standard deviation involves the square root of the variance:
\[
\sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}}
\] -
Engineering:
Engineers use square roots in various calculations, including determining stress and strain in materials and analyzing wave frequencies. For instance, the natural frequency of a system can be calculated using:
\[
f_n = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
\] -
Medicine:
Square roots are used in medical calculations such as determining body surface area (BSA) for medication dosages. The Mosteller formula for BSA is:
\[
BSA = \sqrt{\frac{height \, (cm) \times weight \, (kg)}{3600}}
\]
These examples highlight the importance of square roots in solving practical problems across various disciplines, demonstrating their integral role in both theoretical and applied contexts.
Understanding Irrational Numbers
Irrational numbers are real numbers that cannot be expressed as a simple fraction. This means they cannot be written as the ratio of two integers. Instead, their decimal expansion is infinite and non-repeating.
One of the most well-known examples of an irrational number is the square root of 2, which is approximately 1.41421356... The square root of 115 is another example of an irrational number. It cannot be precisely written as a fraction, and its decimal expansion continues forever without repeating.
Here are some key properties of irrational numbers:
- Non-Terminating and Non-Repeating: The decimal representation of an irrational number never ends and never forms a repeating pattern. For example, the square root of 115 is approximately 10.72380529..., and it continues without repetition.
- Not Rational: Irrational numbers cannot be written as a fraction of two integers. In other words, there are no two integers \(a\) and \(b\) such that the irrational number can be expressed as \(\frac{a}{b}\).
- Dense in Real Numbers: Between any two real numbers, there is at least one irrational number. This makes them densely populated within the set of real numbers.
- Uncountable: The set of irrational numbers is uncountably infinite, meaning there are more irrational numbers than there are rational numbers.
To understand why the square root of 115 is irrational, consider the following mathematical proof outline:
- Assume, for contradiction, that \(\sqrt{115}\) is rational. Then it can be expressed as \(\frac{a}{b}\), where \(a\) and \(b\) are coprime integers (having no common factors other than 1).
- Then \(115 = \left(\frac{a}{b}\right)^2\) or \(115b^2 = a^2\).
- This implies that \(a^2\) is a multiple of 115.
- Since 115 is a prime number, \(a\) must also be a multiple of 115.
- Let \(a = 115k\) for some integer \(k\). Then \(115b^2 = (115k)^2\) or \(115b^2 = 13225k^2\).
- Dividing both sides by 115, we get \(b^2 = 115k^2\).
- This implies that \(b^2\) is also a multiple of 115, and thus \(b\) must be a multiple of 115.
- However, this contradicts our initial assumption that \(a\) and \(b\) are coprime.
Therefore, our assumption that \(\sqrt{115}\) is rational is false. Hence, \(\sqrt{115}\) is irrational.
Irrational numbers play a crucial role in mathematics and science. They help us understand the continuous nature of real numbers and provide insight into various phenomena in the natural world.
Comparison with Other Square Roots
Understanding the square root of 115 can be enriched by comparing it with the square roots of other numbers. Here, we will compare the square root of 115 with the square roots of both perfect squares and other non-perfect squares to gain a broader perspective.
Comparison with Perfect Squares
Perfect squares are numbers whose square roots are integers. Examples include 100, 121, and 144. Let's examine the square roots of these numbers:
- \(\sqrt{100} = 10\)
- \(\sqrt{121} = 11\)
- \(\sqrt{144} = 12\)
Notice that the square root of 115, approximately 10.7238, falls between the square roots of 100 and 121. This tells us that \(\sqrt{115}\) is slightly greater than 10 but less than 11.
Comparison with Non-Perfect Squares
Non-perfect squares are numbers whose square roots are not integers. Examples include 110, 120, and 130. Let's examine the square roots of these numbers:
- \(\sqrt{110} \approx 10.4881\)
- \(\sqrt{120} \approx 10.9545\)
- \(\sqrt{130} \approx 11.4018\)
Again, we see that \(\sqrt{115}\) is between the square roots of 110 and 120. This helps us approximate and understand the magnitude of \(\sqrt{115}\) in relation to other nearby numbers.
Detailed Comparison Table
The following table provides a detailed comparison of the square roots of various numbers, including both perfect and non-perfect squares:
| Number | Square Root | Type |
|---|---|---|
| 100 | 10 | Perfect Square |
| 110 | 10.4881 | Non-Perfect Square |
| 115 | 10.7238 | Non-Perfect Square |
| 120 | 10.9545 | Non-Perfect Square |
| 121 | 11 | Perfect Square |
| 130 | 11.4018 | Non-Perfect Square |
| 144 | 12 | Perfect Square |
From this comparison, we can see that \(\sqrt{115}\) is closer to \(\sqrt{120}\) than to \(\sqrt{110}\), making it useful for estimation and approximation in practical applications.
Understanding how \(\sqrt{115}\) relates to the square roots of both perfect and non-perfect squares helps us appreciate its value and its position within the set of real numbers. This comparative approach enhances our comprehension of square roots and their properties.
Historical Context and Usage
The concept of square roots dates back to ancient civilizations, reflecting humanity's long-standing quest to understand and manipulate numbers. The square root of 115, while specific, fits into this broader historical context, illustrating the evolution of mathematical knowledge and its applications over time.
In ancient Babylon, mathematicians developed some of the earliest methods for approximating square roots, including those of non-square numbers like 115. They used tables and iterative techniques that laid the groundwork for more sophisticated algorithms developed in later centuries.
During the Greek era, mathematicians such as Pythagoras and Euclid expanded on these early methods, contributing significantly to the theory of irrational numbers. The Greeks discovered that the square roots of certain numbers, such as 115, could not be expressed as a simple fraction, thus classifying them as irrational numbers.
In the medieval Islamic world, scholars preserved and expanded upon Greek and Babylonian mathematics. They refined methods for calculating square roots and made significant contributions to algebra and number theory, which included working with irrational numbers.
By the Renaissance, European mathematicians like Fibonacci introduced these concepts to a wider audience, further developing the arithmetic and geometric methods for finding square roots. Fibonacci’s work in his book "Liber Abaci" included the approximation of square roots, helping to spread these mathematical ideas throughout Europe.
In modern times, the calculation of square roots has become essential in various fields such as engineering, physics, and computer science. The square root of 115, approximately 10.7238, is used in various practical applications, from statistical analysis to geometric computations in design and construction.
Overall, the historical context of the square root of 115 highlights the cumulative nature of mathematical knowledge and its pivotal role in advancing human understanding of the natural world.

Căn Bậc Hai Của 115