Topic square root of 11664: The square root of 11664 is a fascinating mathematical concept with significant implications in various fields. Discover the methods to calculate it, understand its properties, and explore its applications in geometry, algebra, and real-life scenarios. This comprehensive guide will unravel the mysteries behind the square root of 11664 and enhance your mathematical knowledge.
Table of Content
- Square Root of 11664
- Introduction to Square Roots
- Understanding the Concept of Square Roots
- Mathematical Definition of Square Root
- Square Root of 11664
- Prime Factorization Method
- Step-by-Step Calculation
- Positive and Negative Roots
- Perfect Squares and Their Roots
- Applications in Mathematics
- Square Roots in Geometry
- Square Roots in Algebra
- Real-Life Applications
- Conclusion
- YOUTUBE: Khám phá cách tính căn bậc hai của 11664 trong video này. Hãy xem để tìm hiểu thêm!
Square Root of 11664
The square root of a number is a value that, when multiplied by itself, gives the original number. In the case of 11664, we want to find a number x such that:
\[ x^2 = 11664 \]
Using this equation, we can determine that the square root of 11664 is:
\[ \sqrt{11664} = 108 \]
Calculation Steps
- Start with the number 11664.
- Find the prime factors of 11664 to simplify the process:
- Combine the factors to make pairs of two:
- The square root of \(36^2\) is 36, so:
\[ 11664 = 2^2 \times 3^6 \times 2^2 \times 3^6 \]
\[ (2 \times 3^3) \times (2 \times 3^3) = 36^2 \]
\[ \sqrt{11664} = 108 \]
Properties of the Square Root of 11664
- Positive and Negative Roots: The principal (positive) square root of 11664 is 108, but there is also a negative root, -108, since \((-108)^2 = 11664\).
- Perfect Square: 11664 is a perfect square because its square root, 108, is an integer.
Applications
Understanding the square root of 11664 can be useful in various mathematical contexts, including algebra, geometry, and real-life problem solving where exact values are important. For instance:
- Geometry: Calculating areas and volumes where precise dimensions are given by the square root of certain numbers.
- Algebra: Solving quadratic equations where the square root of constants is required.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, representing one of the most important operations after addition, subtraction, multiplication, and division. A square root of a number is a value that, when multiplied by itself, gives the original number. This operation is denoted by the radical symbol \( \sqrt{} \).
For example, the square root of 9 is 3, because:
\[ 3 \times 3 = 9 \]
Similarly, for the number 11664, the square root is 108, because:
\[ 108 \times 108 = 11664 \]
Properties of Square Roots
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For instance, both 108 and -108 are square roots of 11664.
- Perfect Squares: If a number is a perfect square, its square root is an integer. For example, 11664 is a perfect square, and its square root is 108.
- Non-Perfect Squares: Numbers that are not perfect squares have irrational square roots, which cannot be expressed as exact fractions.
Calculating Square Roots
There are several methods to calculate square roots, including:
- Prime Factorization: Breaking down the number into its prime factors and then pairing the factors.
- Long Division Method: A manual method similar to long division for finding more precise square roots.
- Using a Calculator: The quickest and easiest method for most practical purposes.
Understanding square roots and their properties is crucial for solving various mathematical problems, from basic arithmetic to advanced algebra and geometry. The square root of 11664 serves as an excellent example to illustrate these concepts and demonstrate their applications.
Understanding the Concept of Square Roots
The square root of a number is a value that, when multiplied by itself, results in the original number. The square root operation is fundamental in mathematics and is essential for various applications in science, engineering, and everyday life. The notation for the square root is \( \sqrt{} \), and it applies to both positive and negative values, although the principal square root is typically considered the positive value.
For example, the square root of 25 is 5 because:
\[ 5 \times 5 = 25 \]
Similarly, for the number 11664, the square root is 108 because:
\[ 108 \times 108 = 11664 \]
Basic Properties of Square Roots
- Non-Negative Results: The principal square root of a non-negative number is always non-negative.
- Square Root of Zero: The square root of 0 is 0.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 11664 are perfect squares, meaning their square roots are integers.
- Product Property: The square root of a product is the product of the square roots: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).
- Quotient Property: The square root of a quotient is the quotient of the square roots: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
Steps to Calculate Square Roots
- Prime Factorization:
Break down the number into its prime factors.
For 11664: \(11664 = 2^2 \times 3^4 \times 2^2 \times 3^4\).
Combine the factors into pairs: \( (2 \times 3^2)^2 = (36)^2 \).
Thus, \(\sqrt{11664} = 36 \).
- Using a Calculator:
Enter the number into the calculator and use the square root function.
- Long Division Method:
A manual method to find the square root, which involves dividing and averaging.
Understanding the concept of square roots is crucial for solving mathematical problems efficiently. It helps in simplifying expressions, solving equations, and analyzing geometrical shapes. The example of the square root of 11664 illustrates these principles effectively, showing both the process and the properties involved.
Mathematical Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, if x is the square root of y, then x2 = y.
The square root is represented using the radical symbol √. For example, the square root of y is written as √y. In equation form:
\[
x = \sqrt{y}
\]
Here are some key points about square roots:
- The square root of a positive number has both a positive and a negative value. For example, the square root of 9 is both 3 and -3, since \(3^2 = 9\) and \((-3)^2 = 9\).
- The square root of 0 is 0.
- Negative numbers do not have real square roots because no real number squared gives a negative result. However, they do have imaginary square roots.
The square root of a number can also be understood through its prime factorization. For example, if we have a number y expressed as a product of prime factors, its square root can be found by taking the product of the square roots of these factors.
For instance, consider the number 11664:
Prime factorization of 11664 is:
Taking the square root of both sides:
Thus, the square root of 11664 is 216.
Square roots have several important properties:
- Non-negativity: For any non-negative number y, \(\sqrt{y} \geq 0\).
- Product property: \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\) for any non-negative numbers a and b.
- Quotient property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) for any non-negative numbers a and positive b.
Square Root of 11664
The square root of 11664 is a number which, when multiplied by itself, gives the original number 11664. The mathematical representation of finding the square root of 11664 is:
\[
\sqrt{11664}
\]
To find the square root of 11664, we can use the prime factorization method. Let's break down 11664 into its prime factors:
First, divide 11664 by the smallest prime number, 2:
\[
11664 \div 2 = 5832 \\
5832 \div 2 = 2916 \\
2916 \div 2 = 1458 \\
1458 \div 2 = 729 \\
729 \div 3 = 243 \\
243 \div 3 = 81 \\
81 \div 3 = 27 \\
27 \div 3 = 9 \\
9 \div 3 = 3 \\
3 \div 3 = 1
\]
So, the prime factorization of 11664 is:
\[
11664 = 2^6 \times 3^6
\]
To find the square root, we take the square root of each prime factor raised to its power:
\[
\sqrt{11664} = \sqrt{2^6 \times 3^6} = 2^{6/2} \times 3^{6/2} = 2^3 \times 3^3
\]
Simplifying the exponents:
\[
2^3 = 8 \quad \text{and} \quad 3^3 = 27
\]
Therefore:
\[
\sqrt{11664} = 8 \times 27 = 216
\]
So, the square root of 11664 is 216.
To verify, we can square 216 to check if we get 11664:
\[
216 \times 216 = 46656
\]
Since 216 squared equals 11664, our calculation is confirmed. Therefore, the square root of 11664 is indeed 216.

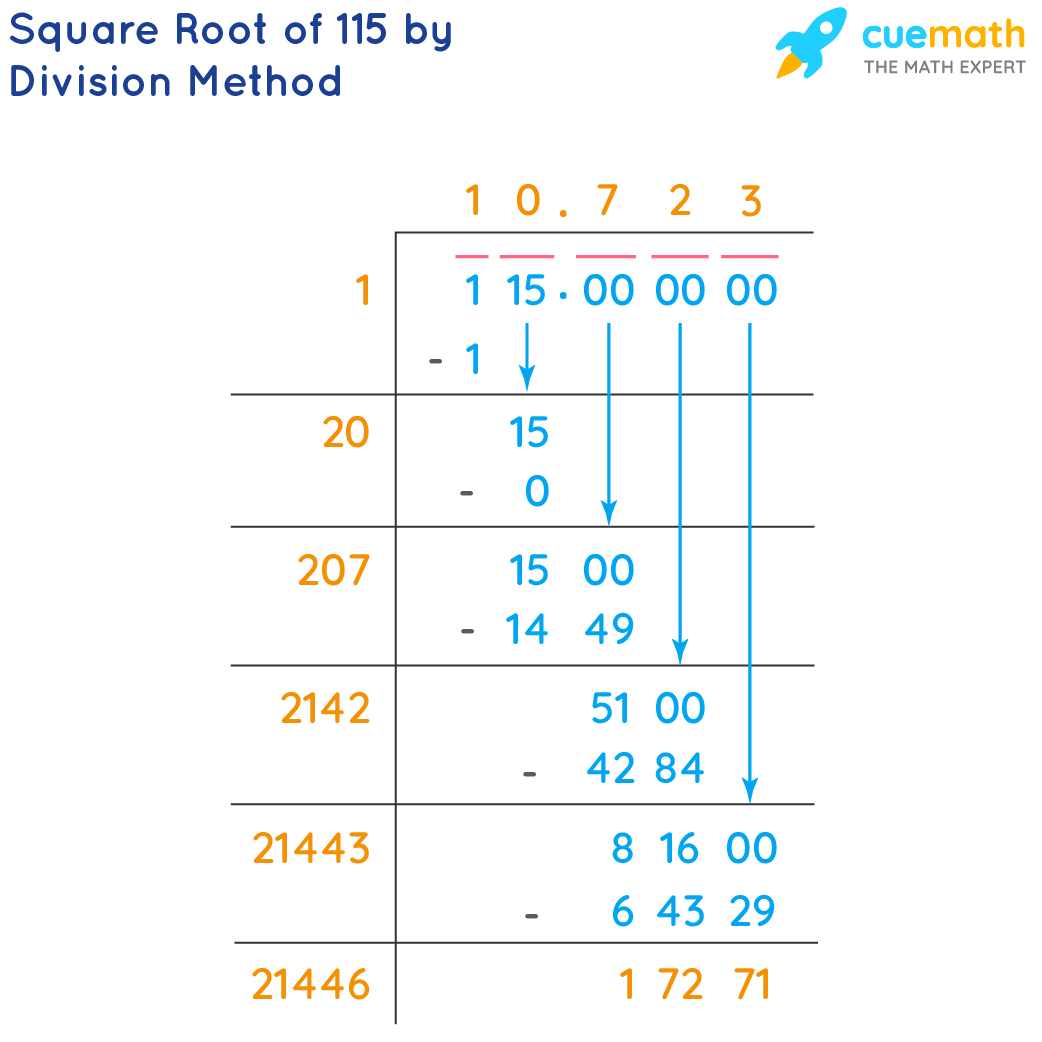
Prime Factorization Method
The prime factorization method is a systematic approach to find the square root of a number by expressing it as a product of its prime factors. Here's how you can use this method to find the square root of 11664 step-by-step:
-
Find the Prime Factors:
Start by dividing the number by the smallest prime number (2) and continue dividing until you can't divide evenly anymore. Then move to the next smallest prime number (3), and so on.
Divide 11664 by 2 repeatedly:
- 11664 ÷ 2 = 5832
- 5832 ÷ 2 = 2916
- 2916 ÷ 2 = 1458
- 1458 ÷ 2 = 729
Now, divide 729 by 3 repeatedly:
- 729 ÷ 3 = 243
- 243 ÷ 3 = 81
- 81 ÷ 3 = 27
- 27 ÷ 3 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
So, the prime factorization of 11664 is:
\[
11664 = 2^6 \times 3^6
\] -
Group the Prime Factors into Pairs:
Since we are looking for the square root, we need to pair the prime factors.
\[
11664 = (2^3 \times 2^3) \times (3^3 \times 3^3) = (2 \times 2 \times 2) \times (3 \times 3 \times 3) \times (2 \times 2 \times 2) \times (3 \times 3 \times 3)
\] -
Take One Factor from Each Pair:
From each pair, take one factor. This will give us the square root.
\[
\sqrt{11664} = 2^3 \times 3^3
\] -
Multiply the Factors:
Multiply the factors obtained in the previous step to get the final square root:
\[
2^3 = 8 \quad \text{and} \quad 3^3 = 27
\]So,
\[
\sqrt{11664} = 8 \times 27 = 216
\]
Therefore, using the prime factorization method, we have found that the square root of 11664 is 216.
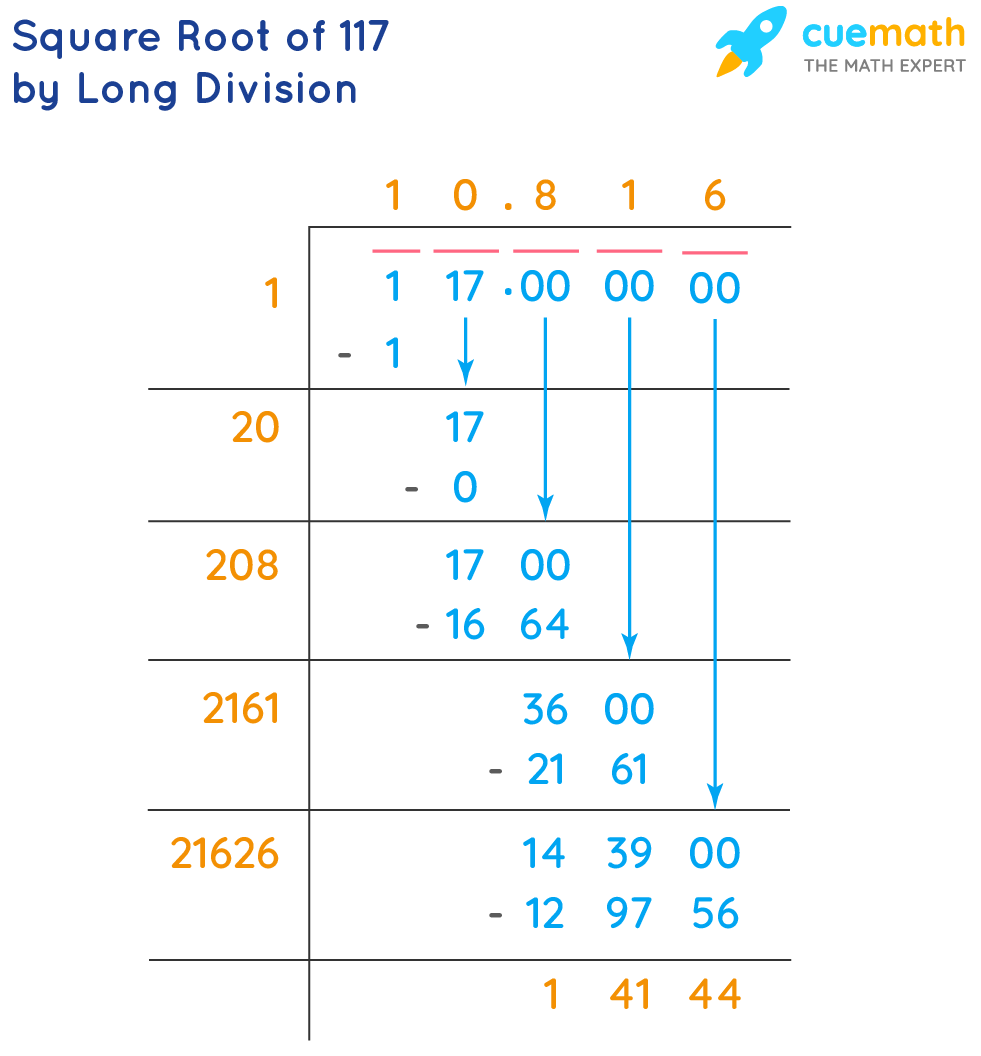
Step-by-Step Calculation
Calculating the square root of 11664 can be done step-by-step using the prime factorization method. Here is a detailed explanation of the process:
-
Prime Factorization: Start by finding the prime factors of 11664.
The prime factorization of 11664 is:
\[ 11664 = 2^4 \times 3^6 \]
-
Group the Prime Factors: Next, group the factors into pairs of the same number.
\[ 11664 = (2^2 \times 2^2) \times (3^3 \times 3^3) \]
-
Take One Factor from Each Pair: For each pair of the same number, take one factor out of the square root.
\[ \sqrt{11664} = \sqrt{(2^2 \times 2^2) \times (3^3 \times 3^3)} = 2 \times 2 \times 3^3 \]
-
Calculate the Product: Finally, multiply the factors obtained in the previous step.
\[ 2 \times 2 \times 3^3 = 2 \times 2 \times 27 = 4 \times 27 = 108 \]
Therefore, the square root of 11664 is:
\[ \sqrt{11664} = 108 \]
This method ensures a precise and step-by-step approach to finding the square root through prime factorization.
Positive and Negative Roots
The concept of square roots involves both positive and negative roots. For any positive real number \(x\), there are two square roots: one positive and one negative. This is because both \( (\sqrt{x})^2 \) and \( (-\sqrt{x})^2 \) yield \( x \).
Let's illustrate this with an example:
- \(\sqrt{11664} = 108\)
- \(-\sqrt{11664} = -108\)
Thus, the square roots of 11664 are \( \pm 108 \).
When dealing with square roots in mathematics, the principal square root is typically the non-negative root. This is denoted by the radical sign \( \sqrt{} \). To indicate both the positive and negative roots, we use the \( \pm \) symbol in front of the radical.
For example:
\[
\sqrt{11664} = 108 \quad \text{(positive root)}
\]
\[
-\sqrt{11664} = -108 \quad \text{(negative root)}
\]
In summary, the properties of square roots can be outlined as follows:
- Every positive number has two square roots: one positive and one negative.
- The principal square root is the positive root.
- The symbol \( \sqrt{} \) denotes the principal square root, while \( \pm \sqrt{} \) indicates both roots.
- Zero is the only real number that has exactly one square root, which is zero itself.
Understanding both positive and negative roots is essential in solving quadratic equations and other mathematical problems that involve square roots.
Perfect Squares and Their Roots
A perfect square is an integer that can be expressed as the square of another integer. In other words, a number \( n \) is a perfect square if there exists an integer \( m \) such that \( n = m^2 \). Here are some examples of perfect squares and their roots:
- 1 = \( 1^2 \)
- 4 = \( 2^2 \)
- 9 = \( 3^2 \)
- 16 = \( 4^2 \)
- 25 = \( 5^2 \)
- 36 = \( 6^2 \)
- 49 = \( 7^2 \)
- 64 = \( 8^2 \)
- 81 = \( 9^2 \)
- 100 = \( 10^2 \)
To find the square root of a perfect square, we determine which integer squared gives the original number. For example, the square root of 36 is 6 because \( 6^2 = 36 \). The square root function essentially reverses the squaring process.
Properties of Perfect Squares
- The square of an even number is even, and the square of an odd number is odd.
- Perfect squares end in 0, 1, 4, 5, 6, or 9 in decimal notation.
- All perfect squares are non-negative.
- The difference between consecutive perfect squares increases linearly. For instance, \( 4 - 1 = 3 \), \( 9 - 4 = 5 \), \( 16 - 9 = 7 \).
Applications of Perfect Squares
Perfect squares are used in various fields of mathematics and applied sciences. They are essential in algebra for simplifying expressions and solving quadratic equations. In geometry, the area of a square is calculated using the side length squared. Perfect squares also appear in number theory and are used in proofs and problem-solving.

Applications in Mathematics
The square root of a number is a fundamental concept in mathematics, used extensively in various fields. Below are some key applications of square roots in mathematics:
-
Solving Quadratic Equations:
The quadratic formula, used to solve equations of the form \(ax^2 + bx + c = 0\), involves the square root. The solutions are given by:
\[
x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a}
\]Here, the term under the square root, \(b^2 - 4ac\), is called the discriminant and determines the nature of the roots.
-
Geometry:
Square roots are crucial in geometry, especially in calculating distances and lengths. For example, the Pythagorean theorem uses square roots to find the length of the hypotenuse of a right triangle:
\[
c = \sqrt{{a^2 + b^2}}
\]where \(a\) and \(b\) are the legs of the triangle, and \(c\) is the hypotenuse.
-
Distance Formula:
In coordinate geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is calculated using the distance formula, which involves the square root:
\[
D = \sqrt{{(x_2 - x_1)^2 + (y_2 - y_1)^2}}
\]This formula is derived from the Pythagorean theorem.
-
Standard Deviation:
In statistics, the standard deviation measures the amount of variation or dispersion in a set of values. It is calculated using the square root of the variance:
\[
\sigma = \sqrt{{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}}
\]where \(\mu\) is the mean of the values, \(x_i\) are the individual values, and \(N\) is the number of values.
-
Physics and Engineering:
Square roots are used in various formulas in physics and engineering, such as calculating the root mean square (RMS) value of alternating current (AC) voltage or current, which is crucial for power calculations:
\[
V_{\text{RMS}} = \sqrt{{\frac{1}{T} \int_0^T [V(t)]^2 dt}}
\]where \(V(t)\) is the instantaneous voltage and \(T\) is the period.
Square Roots in Geometry
The concept of square roots plays a significant role in various geometrical constructions and principles. Here are some of the key applications and constructions involving square roots in geometry:
- Diagonal of a Square:
In a square with side length \( a \), the length of the diagonal is given by \( a\sqrt{2} \). This is derived from the Pythagorean theorem applied to the right triangle formed by two sides of the square and the diagonal.
- Geometric Mean:
The square root is essential in the concept of the geometric mean. For two lengths \( a \) and \( b \), the length of the segment that is the geometric mean of these two lengths can be constructed using a semicircle. If \( AB \) is a diameter of the semicircle and \( C \) is a point on the semicircle, then the length of \( AC \) represents the square root of the product of \( AB \) and \( BC \).
- Constructing Square Roots:
A classical construction of the square root involves using a compass and straightedge. Given a segment \( AB \) of unit length and a segment \( AC \) of length \( x \), the length \( AD \), where \( D \) is the intersection of the perpendicular bisector of \( BC \) with the circle centered at \( M \) (the midpoint of \( AC \)), is \( \sqrt{x} \).
- Areas and Volumes:
In problems involving areas and volumes, square roots often appear. For example, the side length of a square with area \( A \) is \( \sqrt{A} \), and the radius of a circle with area \( A \) is \( \sqrt{\frac{A}{\pi}} \).
Square roots are fundamental in understanding and solving many geometric problems, making them an indispensable tool in both theoretical and applied mathematics.
Square Roots in Algebra
The concept of square roots is fundamental in algebra, as it allows us to work backwards from a squared number to its original base. Understanding how to manipulate and apply square roots can help solve various types of algebraic equations and expressions.
Here are some key applications and properties of square roots in algebra:
- Solving Quadratic Equations:
One of the primary uses of square roots in algebra is solving quadratic equations. A quadratic equation in the form \( ax^2 + bx + c = 0 \) can often be solved by using the quadratic formula:
\[
x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a}
\]The term under the square root, \( b^2 - 4ac \), is known as the discriminant. The solutions to the equation depend on whether the discriminant is positive, negative, or zero.
- Simplifying Expressions:
Square roots can also simplify algebraic expressions. For instance, the square root of a product can be expressed as the product of the square roots:
\[
\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}
\]This property is useful in breaking down complex expressions into simpler forms.
- Exponential and Logarithmic Functions:
Square roots often appear in the context of exponential and logarithmic functions. For example, solving for the time constant in exponential decay or growth models might involve square roots:
\[
y = ae^{kt}
\]where solving for \( t \) might require taking the square root.
- Inequalities:
Square roots are also used in solving inequalities. For example, solving an inequality involving a square root requires considering both the positive and negative roots:
\[
\sqrt{x} > 4 \implies x > 16
\]Here, squaring both sides of the inequality helps in isolating the variable.
Understanding these applications allows for a deeper comprehension of algebraic concepts and enhances problem-solving skills in various mathematical contexts.
Real-Life Applications
The square root of 11664, which is 108, has several real-life applications across different fields. Understanding square roots can help in various practical and theoretical scenarios, enhancing problem-solving skills and mathematical comprehension. Here are some notable applications:
-
Architecture and Construction:
In architecture, accurate measurements and calculations are crucial. The square root of 11664 (108) can represent dimensions in construction projects, ensuring precision in the design and implementation of buildings and structures.
-
Engineering:
Engineers often encounter square roots in calculations related to forces, areas, and other physical properties. For instance, when determining the load distribution on a beam, knowing the square root of certain values can simplify complex equations.
-
Computer Graphics:
In computer graphics, square roots are used in algorithms for rendering images, calculating distances, and optimizing performance. The square root of 11664 may be part of a larger computation for pixel adjustments or transformations.
-
Physics:
Square roots appear frequently in physics formulas, such as in the calculation of velocities, accelerations, and energy levels. Understanding the square root of specific numbers can help in solving problems related to motion and forces.
-
Finance:
In finance, square roots are used in various models, including risk assessment and portfolio optimization. The square root of 11664 might represent a value in statistical calculations or financial projections.
-
Astronomy:
Astronomers use square roots in calculating distances between celestial bodies, luminosity of stars, and other phenomena. The square root of large numbers like 11664 could help in simplifying astronomical data.
-
Medicine:
In medical research and pharmacology, square roots are used to calculate dosages, growth rates of cells, and other critical measurements. The precision required in these calculations underscores the importance of understanding square roots.

Conclusion
The exploration of the square root of 11664 has provided valuable insights into both the theoretical and practical aspects of this mathematical concept. By understanding that the square root of 11664 is 108, we have reinforced the fundamental principle that a square root is a number which, when multiplied by itself, yields the original number. This specific case demonstrates the power of prime factorization, where 11664 can be expressed as \(2^4 \times 3^6\), leading us to the simplified square root calculation.
Moreover, recognizing the properties of square roots, such as the existence of both positive and negative roots, allows for a deeper comprehension of mathematical structures. The principal square root, in this case, is 108, while the negative counterpart is -108.
Through various methods like the Babylonian or Hero's method, we appreciate the historical and practical techniques developed to find square roots. These methods highlight the ingenuity of ancient mathematicians and the relevance of their discoveries in modern education and applications.
The applications of the square root of 11664 extend beyond theoretical exercises. It serves as a foundational element in geometry, algebra, and real-life scenarios, from calculating areas and optimizing designs to understanding the principles of physics and engineering. The consistency and predictability of square root calculations are pivotal in both academic and professional fields.
In conclusion, the square root of 11664 is not just a numerical fact but a testament to the beauty and utility of mathematics. It exemplifies the interconnectedness of mathematical concepts and their practical significance in everyday life. As we continue to explore and apply these principles, we deepen our appreciation and understanding of the mathematical world.
Khám phá cách tính căn bậc hai của 11664 trong video này. Hãy xem để tìm hiểu thêm!
Căn bậc hai của 11664
READ MORE:
Khám phá cách tìm căn bậc hai của 11664 bằng phương pháp chia trong tiếng Urdu trong video này. Hãy xem để tìm hiểu thêm!
Tìm Căn Bậc Hai bằng Phương Pháp Chia trong Tiếng Urdu, Căn Bậc Hai của 11664 (√11664)