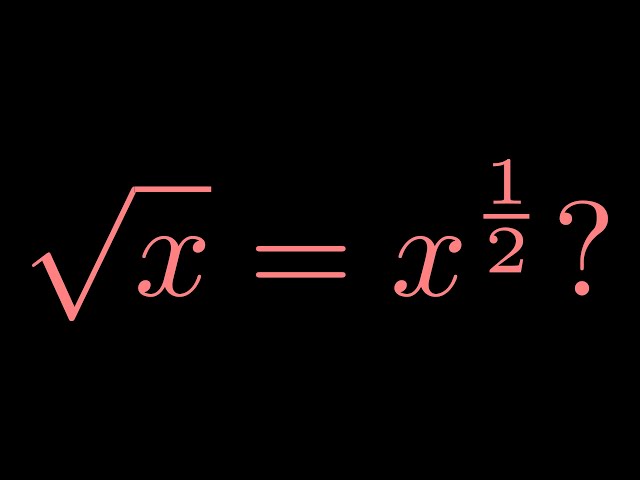Topic what is 169 square root: The square root of 169 is a fundamental mathematical concept that reveals the number 13. Understanding this concept is crucial for various mathematical applications and real-world problem-solving. Dive into this article to explore how to calculate square roots, their importance, and practical examples that showcase the significance of the square root of 169.
Table of Content
- Understanding the Square Root of 169
- Introduction to Square Roots
- Definition of a Square Root
- Importance of Square Roots in Mathematics
- Basic Calculation: Finding the Square Root of 169
- Step-by-Step Guide to Calculating √169
- Mathematical Proof for √169 = 13
- Properties of Perfect Squares
- Real-World Applications of Square Roots
- Square Roots in Geometry
- Common Mistakes in Calculating Square Roots
- Advanced Topics Related to Square Roots
- Conclusion
- YOUTUBE: Tìm hiểu về căn bậc hai của 169 trong video này. Video giải thích chi tiết và dễ hiểu về cách tính căn bậc hai và các ứng dụng thực tế của nó.
Understanding the Square Root of 169
The square root of 169 is a fundamental concept in mathematics. Let's delve into the details and different methods to understand it.
Mathematical Definition
The square root of 169 is the number which, when multiplied by itself, gives 169. Mathematically, it is represented as:
\[
\sqrt{169} = 13
\]
\[
13 \times 13 = 169
\]
Exponential and Radical Forms
The square root of 169 can also be expressed in exponential form and radical form:
- Exponential Form: \(169^{1/2}\) or \(169^{0.5}\)
- Radical Form: \(\sqrt{169}\)
Methods to Calculate the Square Root of 169
-
Prime Factorization
Prime factorization involves breaking down 169 into its prime factors:
\[
169 = 13 \times 13
\]
Thus,
\[
\sqrt{169} = 13
\] -
Long Division Method
The long division method can be used to find the square root of 169 by following these steps:
Step 1: Pair the digits from right to left: (1)(69). Step 2: Find the largest number whose square is less than or equal to the first pair. Here, it is 1. Step 3: Subtract 12 from 1, bring down 69. Step 4: Double the quotient obtained and use it as the new divisor. Here, it becomes 20. Step 5: Find the largest digit that, when added to 20 and multiplied, gives 69 or less. Here, it is 3. Step 6: Complete the division to find the quotient as 13. -
Guess and Check Method
By guessing numbers and refining based on their squares:
- 122 = 144 (too low)
- 142 = 196 (too high)
- 132 = 169 (just right)
Properties of the Square Root of 169
- 169 is a perfect square.
- The square root of 169 is a rational number.
- It lies between the integers 12 and 14.
Applications
Understanding the square root of 169 is crucial in various fields like geometry, algebra, and engineering. It helps in solving problems involving areas, dimensions, and other practical measurements.

READ MORE:
Introduction to Square Roots
Square roots are an essential mathematical concept used to find a number which, when multiplied by itself, results in the given number. For example, the square root of 169 is 13, because \(13 \times 13 = 169\). Square roots are symbolized by the radical sign (√). Here's a detailed introduction to square roots:
- Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\).
- Notation: The square root of \(x\) is denoted as \(\sqrt{x}\).
- Perfect Squares: Numbers like 169, which have integer square roots (13 in this case), are called perfect squares.
To find the square root of a number, follow these steps:
- Estimate: Begin by estimating a number that, when squared, gets close to the target number. For 169, estimate around 12 or 14.
- Refine: Adjust your estimate through trial and error. \(12^2 = 144\) and \(14^2 = 196\). Therefore, the square root is between 12 and 14.
- Exact Calculation: Identify that \(13 \times 13 = 169\), confirming that \(\sqrt{169} = 13\).
Square roots play a crucial role in various mathematical disciplines, including algebra, geometry, and calculus. They are also widely used in practical applications such as engineering, physics, and computer science.
| Number | Square | Square Root |
| 144 | \(12 \times 12\) | 12 |
| 169 | \(13 \times 13\) | 13 |
| 196 | \(14 \times 14\) | 14 |
Understanding square roots helps in simplifying complex equations and solving quadratic equations. Mastery of this concept is essential for advancing in higher mathematics.
Definition of a Square Root
A square root of a number is a value that, when multiplied by itself, yields the original number. It is one of the fundamental operations in mathematics and is denoted using the radical symbol \(\sqrt{}\). Here's a detailed breakdown of the definition and properties of square roots:
- Mathematical Definition: For a given non-negative number \(x\), the square root of \(x\) is a number \(y\) such that \(y^2 = x\). This can be written as:
\[\sqrt{x} = y \quad \text{if and only if} \quad y^2 = x\]
- Principal Square Root: The principal square root is the non-negative root of a number. For example, the principal square root of 169 is 13, as \(13 \times 13 = 169\).
- Positive and Negative Roots: While the principal square root is positive, every positive number actually has two square roots: one positive and one negative. For example:
\[\sqrt{169} = 13 \quad \text{and} \quad -\sqrt{169} = -13\]
- Notation: The square root of a number \(x\) is denoted as \(\sqrt{x}\). For example, \(\sqrt{169} = 13\).
The concept of square roots extends beyond whole numbers to include rational and irrational numbers:
- Whole Numbers: If \(x\) is a perfect square (e.g., 169), then \(\sqrt{x}\) is an integer (e.g., 13).
- Rational Numbers: For non-perfect squares that are rational, the square root is a non-repeating, non-terminating decimal.
- Irrational Numbers: The square root of a non-perfect square (e.g., \(\sqrt{2}\)) is an irrational number.
Here is a table to illustrate square roots of some perfect squares:
| Number | Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
| 121 | 11 |
| 144 | 12 |
| 169 | 13 |
| 196 | 14 |
Understanding the definition of square roots and their properties is fundamental in various branches of mathematics and essential for solving many types of equations.
Importance of Square Roots in Mathematics
Square roots are a cornerstone of mathematics, playing a crucial role in various mathematical concepts and real-world applications. Understanding square roots is fundamental for advancing in many areas of math and science. Here are several reasons why square roots are important:
- Basic Algebra: Square roots are essential in solving quadratic equations. The quadratic formula, used to find the roots of a quadratic equation \(ax^2 + bx + c = 0\), involves square roots:
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
- Geometry: Square roots are used to determine the lengths of sides in right triangles through the Pythagorean theorem:
\[c = \sqrt{a^2 + b^2}\]
where \(c\) is the hypotenuse and \(a\) and \(b\) are the other two sides.
- Measurement and Scaling: Square roots are used in scaling objects, calculating areas, and understanding dimensions in fields such as architecture, engineering, and physics.
- Complex Numbers: Understanding square roots is vital for working with complex numbers, especially when dealing with negative square roots. The imaginary unit \(i\) is defined as:
\[i = \sqrt{-1}\]
- Statistics and Probability: Square roots are used in various statistical measures, such as calculating the standard deviation, which is a measure of the amount of variation or dispersion in a set of values:
\[\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}\]
Square roots also have numerous practical applications:
- Engineering: Engineers use square roots to determine stress, strain, and other properties of materials and structures.
- Physics: Square roots appear in various physical laws and formulas, such as calculating the period of a pendulum:
\[T = 2\pi \sqrt{\frac{L}{g}}\]
where \(T\) is the period, \(L\) is the length of the pendulum, and \(g\) is the acceleration due to gravity.
- Computer Science: Algorithms often utilize square roots, especially in areas such as computer graphics, cryptography, and optimization.
Here is a table summarizing some key areas where square roots are important:
| Field | Application |
| Algebra | Solving quadratic equations |
| Geometry | Calculating side lengths in right triangles |
| Engineering | Determining material properties |
| Physics | Formulas involving time, distance, and force |
| Statistics | Calculating standard deviation |
| Computer Science | Algorithms and optimizations |
Mastering the concept of square roots not only enhances mathematical understanding but also equips individuals with the tools needed to solve complex problems in various scientific and engineering domains.
Basic Calculation: Finding the Square Root of 169
Finding the square root of 169 involves determining a number which, when multiplied by itself, equals 169. Here is a step-by-step guide to understanding and calculating the square root of 169:
- Understand the Concept: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). For 169, we seek a number \( y \) where \( y^2 = 169 \).
- Identify Perfect Squares: Recognize that 169 is a perfect square, meaning its square root is an integer. This can be derived from the properties of squares of whole numbers.
- Estimate: Find two consecutive perfect squares that 169 falls between. Since \( 12^2 = 144 \) and \( 14^2 = 196 \), we know \( 169 \) is between these two squares, narrowing our estimate to around 13.
- Exact Calculation: Verify through multiplication:
\[ 13 \times 13 = 169 \]
Thus, \(\sqrt{169} = 13\).
- Verify Using Factorization: Factor 169 into its prime components.
- 169 is an odd number and divisible by 13:
\[ 169 \div 13 = 13 \]
- Thus,
\[ 169 = 13 \times 13 \]
- 169 is an odd number and divisible by 13:
The square root of 169 is verified as 13, and this calculation can be confirmed by understanding and utilizing basic mathematical principles and multiplication. Here's a summary table to illustrate the calculation:
| Number | Calculation | Result |
| 169 | \(13 \times 13\) | 169 |
This straightforward approach to finding the square root demonstrates the importance of understanding perfect squares and basic multiplication. Mastering these foundational concepts allows for quick and accurate calculations, which are essential in various mathematical applications.
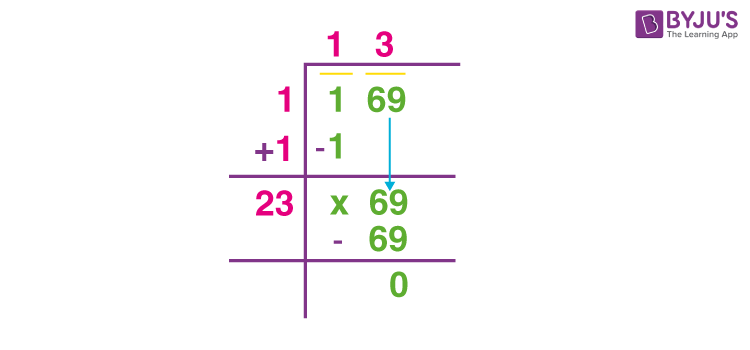
Step-by-Step Guide to Calculating √169
Finding the square root of 169 is a straightforward process, as 169 is a perfect square. Here’s a step-by-step guide to calculating √169:
-
Understand the Problem: You need to find a number that, when multiplied by itself, gives the product 169.
-
Prime Factorization: Start by breaking down 169 into its prime factors.
- 169 is an odd number, so it is not divisible by 2.
- Adding the digits of 169 (1 + 6 + 9 = 16) shows it is not divisible by 3 (since 16 is not divisible by 3).
- 169 ends in a 9, but is not divisible by 5 since it does not end in 0 or 5.
- Divide 169 by 13: \( \frac{169}{13} = 13 \).
This means 169 can be expressed as 13 × 13.
-
Perfect Square Identification: Recognize that 169 is a perfect square because it can be written as the square of an integer (13).
Therefore, \( 169 = 13^2 \).
-
Calculate the Square Root: The square root of a perfect square \( a^2 \) is the integer \( a \).
Hence, \( \sqrt{169} = 13 \).
-
Verification: To confirm, multiply 13 by itself to ensure it equals 169.
\( 13 \times 13 = 169 \).
Therefore, the square root of 169 is 13.
Mathematical Proof for √169 = 13
The mathematical proof for the square root of 169 being 13 can be shown through several steps, including factorization and verification.
-
Prime Factorization: Break down 169 into its prime factors.
- 169 is an odd number, so it is not divisible by 2.
- Sum of digits of 169 is 1 + 6 + 9 = 16, which is not divisible by 3.
- 169 does not end in 0 or 5, so it is not divisible by 5.
- Divide 169 by 13: \( \frac{169}{13} = 13 \). This means 169 can be written as 13 × 13.
Therefore, 169 can be expressed as \( 13 \times 13 \) or \( 13^2 \).
-
Definition of a Square Root: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \).
Given \( x = 169 \), we need to find \( y \) such that \( y^2 = 169 \).
-
Applying the Definition: Since \( 169 = 13^2 \), it follows that:
\( \sqrt{169} = \sqrt{13^2} = 13 \).
-
Verification: To confirm our result, we can square 13 and check if it equals 169.
\( 13 \times 13 = 169 \).
-
Algebraic Proof: Let \( y = 13 \). Then, \( y^2 = 13^2 = 169 \).
Thus, \( \sqrt{169} = 13 \).
Therefore, through prime factorization and definition application, we have proven that the square root of 169 is indeed 13.
Properties of Perfect Squares
A perfect square is an integer that is the square of another integer. In other words, a perfect square results from an integer multiplied by itself. Here are some important properties and characteristics of perfect squares:
- Non-negative Result: The result of squaring any real number is always non-negative. For any integer \( n \), \( n^2 \geq 0 \).
- Even and Odd Patterns: The square of an even number is always even, and the square of an odd number is always odd. For example:
- \( 4^2 = 16 \) (even)
- \( 5^2 = 25 \) (odd)
- End Digits: A perfect square can end only in certain digits in base 10. Specifically, they can end in 0, 1, 4, 5, 6, or 9. For example:
- \( 3^2 = 9 \)
- \( 6^2 = 36 \)
- \( 7^2 = 49 \)
- Sum of Consecutive Odd Numbers: The sum of the first \( n \) odd numbers is always a perfect square. This can be represented as:
\[
1 + 3 + 5 + \cdots + (2n-1) = n^2
\]
For example:
- The sum of the first 4 odd numbers (1 + 3 + 5 + 7) is 16, which is \( 4^2 \).
- Prime Factorization: A number is a perfect square if all the exponents in its prime factorization are even. For instance:
- The prime factorization of 36 is \( 2^2 \times 3^2 \).
- Geometric Interpretation: A perfect square represents the area of a square with integer side lengths. If a square has an area of 169 square units, each side of the square measures \( \sqrt{169} = 13 \) units.
Perfect squares play a crucial role in various mathematical concepts, including solving quadratic equations, analyzing geometric shapes, and understanding number theory.
Real-World Applications of Square Roots
Square roots are fundamental in various real-world applications across different fields. Here are some key examples:
-
Finance:
Square roots are used to calculate stock market volatility, helping investors assess the risk of an investment. The volatility is computed by taking the square root of the variance of stock returns.
-
Architecture and Engineering:
In engineering, square roots help determine the natural frequency of structures like bridges and buildings, which is crucial for predicting their response to loads such as wind and traffic. This application ensures the safety and stability of structures.
-
Science:
Square roots are used in various scientific calculations, such as determining the velocity of moving objects, calculating the intensity of sound waves, and measuring radiation absorption. These calculations help scientists develop new technologies and understand natural phenomena better.
-
Statistics:
In statistics, square roots are essential for calculating standard deviation, which is the square root of the variance. This measure indicates how much data deviates from the mean, aiding in data analysis and decision-making.
-
Geometry:
Square roots are used to compute distances between points in 2D and 3D space, which is essential in fields like navigation and computer graphics. For example, the Pythagorean theorem, which involves square roots, helps in calculating the hypotenuse of a right triangle.
-
Computer Science:
In computer science, square roots are used in algorithms for encryption, image processing, and game physics. These applications include generating secure encryption keys and calculating distances in digital graphics.
-
Cryptography:
Square roots play a role in cryptographic algorithms, including digital signatures and key exchange systems, which are crucial for securing data and communications.
-
Navigation:
Pilots and navigators use square roots to compute distances and directions between points, essential for accurate navigation and plotting flight paths.
-
Electrical Engineering:
Square roots are used to calculate power, voltage, and current in electrical circuits. These calculations are vital for designing and analyzing electrical systems, including power grids and communication networks.
-
Photography:
The aperture of a camera lens is expressed as an f-number, which involves square roots. Changing the f-number by a factor of two changes the amount of light entering the camera by a factor of four, impacting exposure and image quality.
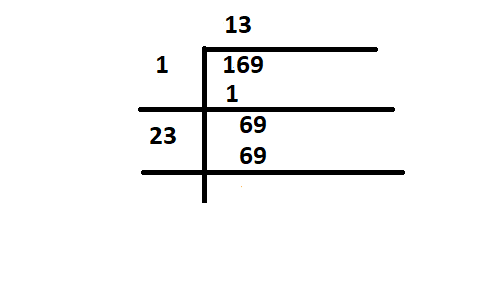
Square Roots in Geometry
The concept of square roots is fundamental in geometry, where they are often used to determine lengths, areas, and other geometric properties. Below are some key applications of square roots in geometric contexts:
- Calculating the Side Length of a Square: Given the area of a square, the side length can be found by taking the square root of the area. For example, if the area of a square is 169 square units, the side length is √169 = 13 units.
- Distance Between Points: In coordinate geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is calculated using the distance formula:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
This formula is derived from the Pythagorean theorem and involves square roots to find the Euclidean distance between the points. - Pythagorean Theorem: One of the most famous applications of square roots in geometry is the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides:
\[
c^2 = a^2 + b^2 \implies c = \sqrt{a^2 + b^2}
\]
Here, \(c\) is the hypotenuse, and \(a\) and \(b\) are the other two sides. This theorem is used to find the length of one side of a triangle when the lengths of the other two sides are known. - Area and Diagonal of a Rectangle: For a rectangle, the length of the diagonal can be found using the Pythagorean theorem. If the length and width of the rectangle are known, the diagonal \(d\) is given by:
\[
d = \sqrt{l^2 + w^2}
\]
where \(l\) is the length and \(w\) is the width. This uses square roots to determine the diagonal distance across the rectangle. - Circles and Spheres: Square roots are also used to calculate the radius of a circle or sphere when the area or volume is known. For example, the radius \(r\) of a circle with area \(A\) is:
\[
r = \sqrt{\frac{A}{\pi}}
\]
Similarly, for a sphere with volume \(V\), the radius is:\[
r = \sqrt[3]{\frac{3V}{4\pi}}
\]
Understanding the role of square roots in these geometric contexts helps in solving various practical problems involving measurements and distances.
Common Mistakes in Calculating Square Roots
Calculating square roots can sometimes lead to common errors, especially if the underlying concepts are misunderstood. Here are some typical mistakes and how to avoid them:
- Misinterpreting the Square Root Symbol:
Often, students confuse the square root of a number with its half. For example, \(\sqrt{25}\) is sometimes incorrectly thought to be \(5/2\). The correct interpretation is that \(\sqrt{25} = 5\).
- Incorrectly Simplifying Expressions:
Errors can occur when simplifying expressions under the square root. For instance, \(\sqrt{x + y} \neq \sqrt{x} + \sqrt{y}\). An example to illustrate this is \(\sqrt{9 + 16} \neq \sqrt{9} + \sqrt{16}\), as \(\sqrt{25} = 5\) while \(3 + 4 = 7\).
- Incorrectly Adding Square Roots:
Students sometimes add square roots incorrectly. For example, \(3\sqrt{5} + 2\sqrt{5} \neq 6\sqrt{5}\). The correct sum is \(5\sqrt{5}\), since the coefficients (3 and 2) should be added first.
- Forgetting to Square Both Sides of an Equation:
When solving equations involving square roots, it’s crucial to square both sides correctly. For example, solving \(\sqrt{x} = 3\) should be done by squaring both sides to get \(x = 9\).
- Ignoring Negative Results:
Students often forget that squaring a negative number results in a positive number. For example, \(( -3 )^2 = 9\), not \(-9\).
- Misunderstanding the Order of Operations:
Incorrect application of the order of operations can lead to mistakes. For example, when calculating \(\sqrt{4 \times 9}\), the correct process is to first multiply and then take the square root: \(\sqrt{36} = 6\), not \(\sqrt{4} \times \sqrt{9} = 2 \times 3 = 6\).
- Errors with Decimal Numbers:
Errors frequently occur when dealing with decimals. For example, \(0.2^2 \neq 0.4\); instead, \(0.2 \times 0.2 = 0.04\).
To avoid these common mistakes, it is important to practice regularly, understand the properties of square roots, and carefully apply mathematical rules. Ensuring a strong foundation in these concepts will help prevent errors and improve accuracy in calculations.
Advanced Topics Related to Square Roots
Square roots extend beyond basic arithmetic into various advanced mathematical concepts and applications. Here are some advanced topics related to square roots:
- Imaginary and Complex Numbers: When dealing with the square roots of negative numbers, we enter the realm of imaginary numbers. The square root of -1 is denoted as \(i\), leading to complex numbers of the form \(a + bi\).
- Polynomial Roots: Understanding square roots is crucial in solving polynomial equations. For instance, the roots of a quadratic equation \(ax^2 + bx + c = 0\) can be found using the quadratic formula, which involves a square root: \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\).
- Eigenvalues and Eigenvectors: In linear algebra, square roots appear when calculating eigenvalues and eigenvectors of a matrix, particularly through the characteristic polynomial.
- Square Root Functions and Transformations: In function analysis, the square root function \(f(x) = \sqrt{x}\) is a fundamental example of a non-linear function, influencing transformations and compositions of functions.
- Square Roots in Calculus: Square roots frequently appear in integration and differentiation, particularly in integrals involving radical expressions and in the calculation of arc lengths.
- Continuity and Limits: The behavior of square root functions is a common topic in the study of limits and continuity in calculus. Understanding how these functions behave as their input approaches certain values is essential.
- Square Roots in Geometry and Trigonometry: In geometry, square roots are used in the Pythagorean theorem and distance formulas. In trigonometry, they appear in the calculation of sine, cosine, and other trigonometric functions.
- Square Roots of Matrices: In advanced linear algebra, the concept of a square root of a matrix is used, which involves finding a matrix \(B\) such that \(B^2 = A\), where \(A\) is the given matrix.
These topics illustrate the broad and deep applications of square roots in higher mathematics, showing their importance in both theoretical and applied contexts.
Conclusion
The exploration of the square root of 169 has provided us with a comprehensive understanding of this mathematical concept and its applications. We have delved into the definition and significance of square roots, specifically focusing on the example of √169, which equals 13. This process has illustrated both the theoretical and practical aspects of square roots.
Through step-by-step calculations, we demonstrated how to determine the square root of a perfect square. Furthermore, we explored the mathematical proof confirming that √169 is indeed 13, underscoring the importance of understanding these fundamental principles in mathematics.
We also examined the properties of perfect squares, noting how they simplify the process of finding square roots, and discussed the wide range of real-world applications, from geometry to various fields requiring precise calculations.
In geometry, square roots play a crucial role in solving problems related to area and length, helping to bridge the gap between algebraic and geometric understanding. Additionally, we highlighted common mistakes made during square root calculations and provided tips on how to avoid them, ensuring accuracy in mathematical computations.
Moreover, we ventured into advanced topics related to square roots, including their behavior in complex numbers and their applications in higher-level mathematics. This exploration has not only deepened our understanding but also highlighted the interconnectedness of mathematical concepts.
In conclusion, the study of square roots, exemplified by the calculation of √169, reveals the elegance and utility of mathematics. Whether in academic settings or real-world applications, mastering the concept of square roots equips us with essential tools for solving a wide array of problems, fostering both logical thinking and practical problem-solving skills.
Tìm hiểu về căn bậc hai của 169 trong video này. Video giải thích chi tiết và dễ hiểu về cách tính căn bậc hai và các ứng dụng thực tế của nó.
Căn Bậc Hai Của 169
READ MORE:
Hướng dẫn cách tính căn bậc hai của 169 nhanh chóng và chính xác bằng phương pháp ngắn gọn.
Cách tính căn bậc hai của 169 bằng phương pháp ngắn gọn