Topic is 169 a square number: Have you ever wondered if 169 is a square number? The answer is both intriguing and enlightening. In this article, we will explore the concept of square numbers, provide a clear mathematical explanation, and reveal why 169 holds a special place in this category. Join us on this mathematical journey!
Table of Content
- Is 169 a Square Number?
- Introduction to Square Numbers
- Understanding Square Numbers
- Definition of a Square Number
- Examples of Square Numbers
- Mathematical Properties of Square Numbers
- Calculating Square Numbers
- Is 169 a Square Number?
- Mathematical Proof that 169 is a Square Number
- Prime Factorization Method
- Visual Representation of 169 as a Square Number
- Applications of Square Numbers
- Square Numbers in Real Life
- Frequently Asked Questions about Square Numbers
- YOUTUBE: Khám phá video Căn Bậc Hai 169 để hiểu rõ hơn về số 169 có phải là số chính phương hay không.
Is 169 a Square Number?
The number 169 is indeed a square number. A square number, also known as a perfect square, is an integer that is the square of another integer.
Mathematical Explanation
To determine if 169 is a square number, we find its square root:
\[ \sqrt{169} = 13 \]
Since 13 is an integer, 169 is a perfect square.
Properties of 169
- 169 can be expressed as \(13^2\).
- It is the product of 13 multiplied by itself: \(13 \times 13 = 169\).
- The factors of 169 are 1, 13, and 169.
- 169 is an odd number and a composite number.
Perfect Squares List (1 to 100)
| Number | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
... and so on up to 100.
Interesting Facts
- All perfect squares have an odd number of total factors.
- Every perfect square can be represented as a sum of consecutive odd numbers.
- The square root of a perfect square is always an integer.
Conclusion
In summary, 169 is a perfect square as it can be expressed as \(13^2\). Understanding perfect squares is fundamental in mathematics, and they have unique properties that distinguish them from other numbers.

READ MORE:
Introduction to Square Numbers
Square numbers, also known as perfect squares, are the product of an integer multiplied by itself. These numbers are fundamental in various branches of mathematics and appear frequently in number theory, algebra, and geometry.
For example, consider the number 169. To determine if it is a square number, we need to find if there is an integer \( n \) such that \( n \times n = 169 \). Indeed, \( 13 \times 13 = 169 \), making 169 a square number.
Here is a step-by-step approach to understand square numbers:
- Definition: A number \( n \) is a square number if there exists an integer \( k \) such that \( n = k^2 \).
- Examples: Common square numbers include \( 1, 4, 9, 16, 25, 36, \) and so on. For instance, \( 4 = 2^2 \) and \( 25 = 5^2 \).
- Properties:
- Square numbers are always non-negative.
- The square of an even number is even, and the square of an odd number is odd.
- Square numbers have an odd number of total divisors.
- Visualization:
Visualizing square numbers can help in understanding their properties. For example, arranging 16 objects in a 4 by 4 grid shows that 16 is a square number.
● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●
Understanding square numbers is crucial for delving deeper into mathematical concepts. Recognizing patterns and properties in square numbers lays a solid foundation for advanced studies.
Understanding Square Numbers
Square numbers are a fundamental concept in mathematics, defined as the product of an integer multiplied by itself. To better understand square numbers, let's explore their characteristics, properties, and methods to identify them.
Here is a detailed approach to understanding square numbers:
- Definition: A number \( n \) is considered a square number if there exists an integer \( k \) such that \( n = k^2 \). For example, \( 169 \) is a square number because \( 13 \times 13 = 169 \) or \( 169 = 13^2 \).
- Mathematical Expression: The general form of a square number is \( n = k^2 \), where \( k \) is an integer. Using Mathjax, this can be represented as:
\[
n = k^2
\] - Examples of Square Numbers:
- \( 1 = 1^2 \)
- \( 4 = 2^2 \)
- \( 9 = 3^2 \)
- \( 16 = 4^2 \)
- \( 25 = 5^2 \)
- \( 36 = 6^2 \)
- Properties of Square Numbers:
- Square numbers are always non-negative because the square of any real number is non-negative.
- The square of an even number is even, and the square of an odd number is odd.
- Square numbers have an odd number of total divisors. For example, \( 36 \) has the divisors \( 1, 2, 3, 4, 6, 9, 12, 18, 36 \).
- Identifying Square Numbers:
- Calculate the square root of the number.
- Check if the square root is an integer.
- If the square root is an integer, then the number is a square number.
- Visualization:
Visual aids can help in understanding square numbers. For example, arranging objects into a perfect square shape visually demonstrates that the number is a square number.
● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●
In summary, square numbers are integral to mathematics, providing a basis for understanding more complex concepts. Recognizing and working with square numbers is essential for progressing in mathematical studies.
Definition of a Square Number
A square number, also known as a perfect square, is defined as a number that can be expressed as the product of an integer with itself. In other words, a number \( n \) is a square number if there exists an integer \( k \) such that \( n = k^2 \).
Let's break down the definition step by step:
- Integer: An integer is a whole number that can be positive, negative, or zero. Examples of integers include -3, 0, 7, and 13.
- Multiplication: Multiplication is a mathematical operation where a number is added to itself a certain number of times. For instance, \( 3 \times 3 \) means adding 3 three times: \( 3 + 3 + 3 \).
- Product: The result of multiplying two numbers. In our context, the product of an integer \( k \) with itself is \( k \times k \).
To illustrate, consider the number 169:
- Find an integer \( k \) such that \( k \times k = 169 \).
- Calculate the square root of 169. The square root of 169 is 13.
- Verify that \( 13 \) is an integer and that \( 13 \times 13 = 169 \).
Therefore, 169 is a square number because it can be written as \( 169 = 13^2 \).
Here are more examples of square numbers:
- \( 1 = 1^2 \)
- \( 4 = 2^2 \)
- \( 9 = 3^2 \)
- \( 16 = 4^2 \)
- \( 25 = 5^2 \)
- \( 36 = 6^2 \)
In summary, a square number is any number that fits the form \( k^2 \), where \( k \) is an integer. This concept is fundamental in various fields of mathematics, from basic arithmetic to advanced algebra and geometry.
Examples of Square Numbers
Square numbers, or perfect squares, are integers that are the product of an integer multiplied by itself. Understanding square numbers can be greatly aided by examining specific examples. Here, we will explore several square numbers and their properties.
Here are some examples of square numbers:
- 1: \( 1 = 1 \times 1 = 1^2 \)
- 4: \( 4 = 2 \times 2 = 2^2 \)
- 9: \( 9 = 3 \times 3 = 3^2 \)
- 16: \( 16 = 4 \times 4 = 4^2 \)
- 25: \( 25 = 5 \times 5 = 5^2 \)
- 36: \( 36 = 6 \times 6 = 6^2 \)
- 49: \( 49 = 7 \times 7 = 7^2 \)
- 64: \( 64 = 8 \times 8 = 8^2 \)
- 81: \( 81 = 9 \times 9 = 9^2 \)
- 100: \( 100 = 10 \times 10 = 10^2 \)
- 121: \( 121 = 11 \times 11 = 11^2 \)
- 144: \( 144 = 12 \times 12 = 12^2 \)
- 169: \( 169 = 13 \times 13 = 13^2 \)
To illustrate further, let's take a closer look at a few of these square numbers:
- 9:
Nine is a square number because it can be written as \( 3^2 \). This means that when the integer 3 is multiplied by itself, the product is 9.
● ● ● ● ● ● ● ● ● - 16:
Sixteen is another example of a square number, represented as \( 4^2 \). Multiplying the integer 4 by itself yields 16.
● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● - 25:
Twenty-five is a square number because it equals \( 5^2 \). This means that multiplying 5 by itself results in 25.
● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●
These examples demonstrate how square numbers are formed and highlight their unique properties. Recognizing these numbers helps in various mathematical applications and problem-solving scenarios.

Mathematical Properties of Square Numbers
Square numbers possess several unique mathematical properties that distinguish them from other types of numbers. Understanding these properties is essential for recognizing patterns and solving mathematical problems. Here, we explore the key properties of square numbers in detail.
- Non-Negative Values:
Square numbers are always non-negative. This is because the product of any integer, whether positive or negative, multiplied by itself is always non-negative. Mathematically, \( n = k^2 \geq 0 \) for any integer \( k \).
- Parity:
The parity of a square number depends on the parity of the original integer. If \( k \) is even, \( k^2 \) is also even. If \( k \) is odd, \( k^2 \) is odd. For example:
- Even integer: \( 4 \times 4 = 16 \) (even)
- Odd integer: \( 5 \times 5 = 25 \) (odd)
- Number of Divisors:
Square numbers have an odd number of total divisors. This is because the divisors of square numbers pair up symmetrically around the square root, with the square root itself being unpaired. For example, 36 has the divisors 1, 2, 3, 4, 6, 9, 12, 18, and 36, totaling 9 (an odd number).
- Sum of Odd Numbers:
Square numbers can be expressed as the sum of consecutive odd numbers. For example:
- \( 1 = 1 \)
- \( 4 = 1 + 3 \)
- \( 9 = 1 + 3 + 5 \)
- \( 16 = 1 + 3 + 5 + 7 \)
- \( 25 = 1 + 3 + 5 + 7 + 9 \)
- Difference of Consecutive Squares:
The difference between consecutive square numbers follows a specific pattern. The difference between \( k^2 \) and \( (k+1)^2 \) is \( 2k + 1 \). For example:
- \( (2+1)^2 - 2^2 = 9 - 4 = 5 \)
- \( (3+1)^2 - 3^2 = 16 - 9 = 7 \)
- \( (4+1)^2 - 4^2 = 25 - 16 = 9 \)
- Units Digit Pattern:
The units digit of square numbers follows a predictable pattern. Specifically, the square of a number ending in 0, 1, 5, or 6 will end in the same digit. For example:
- \( 10^2 = 100 \) (ends in 0)
- \( 11^2 = 121 \) (ends in 1)
- \( 15^2 = 225 \) (ends in 5)
- \( 16^2 = 256 \) (ends in 6)
In summary, square numbers exhibit a variety of interesting mathematical properties that make them a key concept in number theory and other mathematical disciplines. Recognizing these properties helps in solving complex problems and understanding the structure of numbers.
Calculating Square Numbers
Calculating square numbers is a straightforward process that involves multiplying an integer by itself. This section will guide you through the steps to determine whether a number is a square number and how to calculate it using both basic multiplication and mathematical functions.
Here is a step-by-step approach to calculating square numbers:
- Select an Integer:
Choose any integer \( n \). For example, let's select \( n = 13 \).
- Multiply the Integer by Itself:
Calculate the product of the integer with itself. Using Mathjax, this can be represented as:
\[
n \times n = n^2
\]For \( n = 13 \):
\[
13 \times 13 = 169
\] - Verify the Result:
Check if the result is a perfect square. You can verify this by finding the square root of the result and ensuring it is an integer. Using Mathjax:
\[
\sqrt{169} = 13
\]Since 13 is an integer, 169 is confirmed as a square number.
To further illustrate, here are some examples of calculating square numbers:
- Example 1: Calculate \( 7^2 \):
\[
7 \times 7 = 49
\]Verify: \[
\sqrt{49} = 7
\] - Example 2: Calculate \( 8^2 \):
\[
8 \times 8 = 64
\]Verify: \[
\sqrt{64} = 8
\] - Example 3: Calculate \( 12^2 \):
\[
12 \times 12 = 144
\]Verify: \[
\sqrt{144} = 12
\]
Using Mathematical Functions:
Modern calculators and programming languages provide built-in functions to calculate square numbers. For instance, in Python, you can use the ** operator or the pow() function:
Example code:
n = 13 |
square = n ** 2 |
print(square) # Output: 169 |
In summary, calculating square numbers is a simple process of multiplying an integer by itself. Verifying the result ensures accuracy, and utilizing mathematical functions can simplify the calculation in various applications.
Is 169 a Square Number?
Yes, 169 is a square number. A square number, also known as a perfect square, is an integer that is the square of an integer. In other words, it is the product of an integer with itself. Let's explore this in more detail.
Step-by-Step Explanation
To determine if 169 is a square number, we need to find an integer \( n \) such that:
\( n^2 = 169 \)
- We start by estimating the square root of 169. The square root of 169 is denoted as \( \sqrt{169} \).
- Calculate the square root:
\( \sqrt{169} = 13 \)
- Verify by squaring 13:
\( 13 \times 13 = 169 \)
Since 13 is an integer and \( 13 \times 13 = 169 \), we can conclude that 169 is indeed a square number.
Mathematical Proof that 169 is a Square Number
We can also use the prime factorization method to verify that 169 is a square number.
- Find the prime factors of 169:
- 169 can be divided by 13: \( 169 \div 13 = 13 \)
- So, 169 can be written as \( 13 \times 13 \) or \( 13^2 \)
- Since the prime factorization of 169 is \( 13^2 \), it confirms that 169 is a perfect square.
Visual Representation of 169 as a Square Number
To visualize this, imagine a grid of 13 rows and 13 columns:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
This 13x13 grid visually represents 169 as a perfect square.
Mathematical Proof that 169 is a Square Number
To prove that 169 is a square number, we need to show that it can be expressed as the square of an integer. Here are a few mathematical approaches to demonstrate this:
Prime Factorization Method
We begin with the prime factorization of 169:
- 169 is divided by the smallest prime number, 2. Since 169 is odd, it is not divisible by 2.
- Next, we try the next smallest prime numbers, 3, 5, 7, and 11. Since 169 is not divisible by any of these, we proceed to 13.
- 169 divided by 13 equals 13, so the factorization of 169 is 13 × 13.
Thus, \(169 = 13^2\), showing that 169 is indeed a square number.
Square Root Method
We can also confirm this by finding the square root of 169:
\[\sqrt{169} = 13\]
Since 13 is an integer, 169 is a perfect square.
Visual Representation
Another way to verify this is by visual representation. Imagine a square grid where each side of the square contains 13 units:
| 13 |
The area of this grid is \(13 \times 13 = 169\), proving that 169 is a square number.
Conclusion
From the prime factorization method, the square root method, and the visual representation, we can conclusively say that 169 is a square number because it can be expressed as \(13^2\).
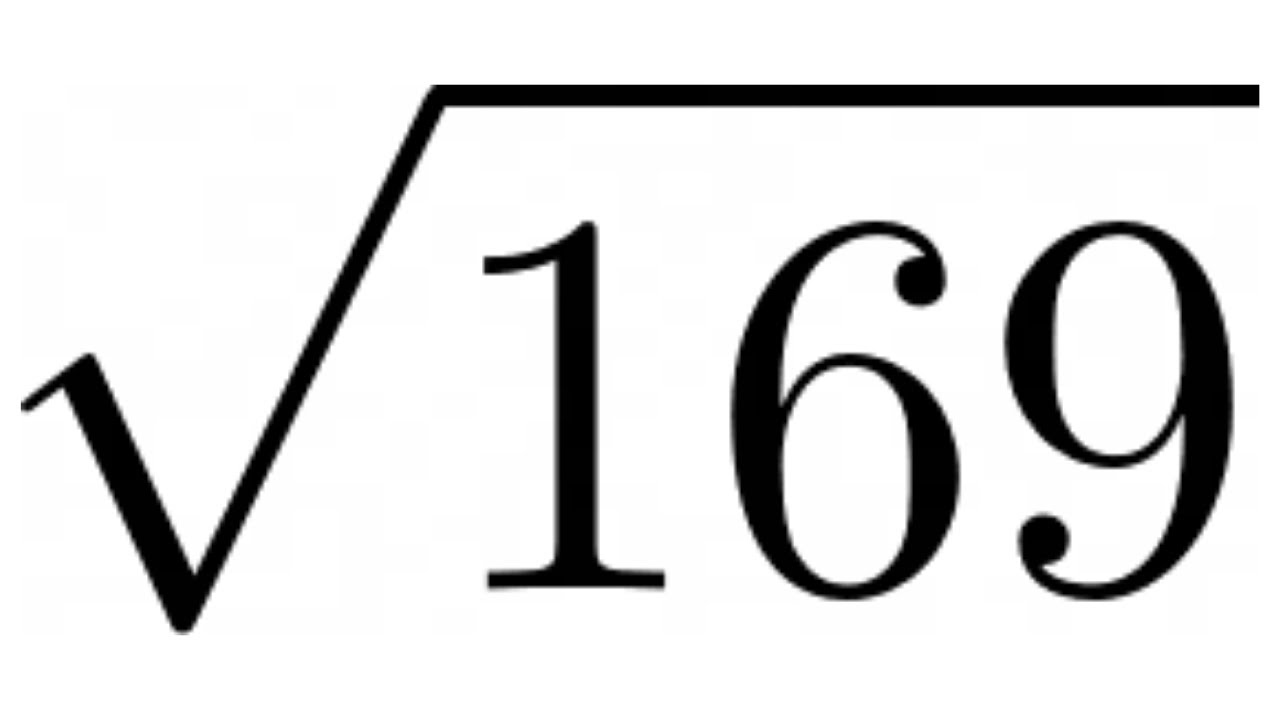
Prime Factorization Method
The prime factorization method is a process of breaking down a number into a product of its prime factors. Here, we will use this method to determine if 169 is a square number.
- Start by identifying the smallest prime number that can divide 169. The prime numbers are 2, 3, 5, 7, 11, 13, etc.
- Since 169 is odd, it is not divisible by 2. Checking for divisibility by 3, 5, 7, and 11 also shows no exact division. However, 169 is divisible by 13:
- Now, we have 13 as a quotient. Repeat the process for the quotient. We divide 13 by 13:
- Since we have reached 1, we can conclude that the prime factors of 169 are 13 and 13.
\[ 169 \div 13 = 13 \]
\[ 13 \div 13 = 1 \]
Thus, the prime factorization of 169 is:
\[ 169 = 13 \times 13 = 13^2 \]
This shows that 169 is a perfect square, as it can be expressed as the square of the prime number 13.
Prime Factorization Using a Factor Tree
We can also visualize the prime factorization using a factor tree:
| 169 | |
| |↓| | |
| 13 | * 13 |
This tree confirms that 169 breaks down into 13 multiplied by 13.
In conclusion, both the division method and the factor tree method show that the prime factorization of 169 is \(13^2\), verifying that 169 is indeed a square number.
Visual Representation of 169 as a Square Number
To visually represent 169 as a square number, we can arrange 169 dots in a perfect square grid. This means forming a 13 by 13 grid, since the square root of 169 is 13.
Here's a step-by-step breakdown:
- Calculate the square root of 169:
- Arrange 169 dots into a 13 by 13 grid, forming a perfect square:
This visual representation helps to see that 169 is indeed a square number because it can be arranged into a perfect square grid:
|
|
The above grid shows 169 dots arranged in a 13 by 13 layout, confirming that 169 is a square number. This grid is a perfect visual proof that the number 169 is a square number.
Applications of Square Numbers
Square numbers have numerous applications across various fields, illustrating their importance beyond theoretical mathematics. Here are some key applications:
- Geometry:
Square numbers are fundamental in geometry, particularly in calculating areas. The area of a square is found by squaring the length of one of its sides. For instance, if a square has a side length of 4 units, its area is \(4^2 = 16\) square units.
- Algebra:
In algebra, square numbers are used in solving quadratic equations. The quadratic formula, \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\), involves calculating the square root of the discriminant (\(b^2 - 4ac\)), which determines the nature of the roots.
- Computer Science:
Square numbers are used in data structure sizing and algorithm complexity analysis. For example, searching algorithms such as binary search can benefit from understanding square roots to efficiently divide and conquer data sets.
- Physics:
Square numbers are crucial in physics, especially in the study of waves and vibrations. The energy of a wave is proportional to the square of its amplitude, making square numbers essential in calculating wave properties.
- Architecture and Construction:
Architects and engineers use square numbers to design and analyze structures. For example, the area of rooms and spaces often relies on square measurements to ensure accuracy and symmetry in design.
- Everyday Life:
In everyday contexts, square numbers help in understanding dimensions and areas. For instance, when determining the size of an apartment, knowing the area (e.g., 625 square feet) allows one to visualize it as a 25x25 square.
These applications demonstrate the versatility and significance of square numbers in both practical and theoretical contexts.
Square Numbers in Real Life
Square numbers play a significant role in various real-life applications and are encountered in numerous fields. Here are some practical examples:
- Geometry and Area Calculation:
In geometry, the concept of square numbers is directly used to calculate the area of squares. The area of a square is given by the square of the length of its side. For example, if the side of a square is 5 units, the area is \(5^2 = 25\) square units.
- Construction and Architecture:
Square numbers are essential in construction and architecture for creating perfectly square layouts. Ensuring corners are right angles and areas are calculated correctly often involves the use of square numbers.
- Computer Science:
In computer graphics, square numbers are used in pixel counts for screens and in algorithms that involve spatial calculations. For instance, a 16x16 pixel icon contains \(16^2 = 256\) pixels.
- Games and Puzzles:
Board games like chess and checkers use square grids. A standard chessboard has 8 rows and 8 columns, making \(8^2 = 64\) squares. Sudoku puzzles also involve understanding square grids and regions.
- Mathematics and Education:
Square numbers are fundamental in teaching basic arithmetic and algebra. They help students understand the properties of numbers and operations.
- Technology and Engineering:
In technology, square numbers are used in various algorithms, such as in sorting algorithms and data structure designs where understanding the optimal number of operations or memory allocation involves squares.
These applications demonstrate the importance of square numbers in everyday life and various professional fields, highlighting their versatility and utility.

Frequently Asked Questions about Square Numbers
-
What is a square number?
A square number is an integer that is the product of some integer with itself. For example, 1, 4, 9, 16, and 25 are all square numbers because they can be written as 1×1, 2×2, 3×3, 4×4, and 5×5, respectively.
-
Is 169 a square number?
Yes, 169 is a square number. It can be expressed as 13×13.
-
How can you determine if a number is a square number?
To determine if a number is a square number, find the square root of the number. If the square root is an integer, then the number is a square number. For example, the square root of 169 is 13, which is an integer, so 169 is a square number.
-
What are the first ten square numbers?
The first ten square numbers are:
- 1 (1×1)
- 4 (2×2)
- 9 (3×3)
- 16 (4×4)
- 25 (5×5)
- 36 (6×6)
- 49 (7×7)
- 64 (8×8)
- 81 (9×9)
- 100 (10×10)
Can negative numbers be square numbers?
No, negative numbers cannot be square numbers because the product of two integers (whether positive or negative) is always a positive number. Therefore, square numbers are always non-negative.
-
How are square numbers used in real life?
Square numbers are used in various fields including geometry, algebra, and real-life applications such as calculating areas of squares, understanding quadratic equations, and in digital signal processing.
-
What is the difference between a square number and a perfect square?
There is no difference between a square number and a perfect square; both terms are used interchangeably to describe an integer that is the square of another integer.
-
How do you find the next square number after a given square number?
To find the next square number after a given square number, add 1 to the square root of the given square number, then square the result. For example, the next square number after 169 (which is 13×13) is (13+1)×(13+1) = 14×14 = 196.
Khám phá video Căn Bậc Hai 169 để hiểu rõ hơn về số 169 có phải là số chính phương hay không.
Căn Bậc Hai 169
READ MORE:
Tìm hiểu cách tính căn bậc hai của 169 bằng phương pháp nhanh và chính xác trong video này.
Cách Tính Căn Bậc Hai của 169 Bằng Phương Pháp Nhanh