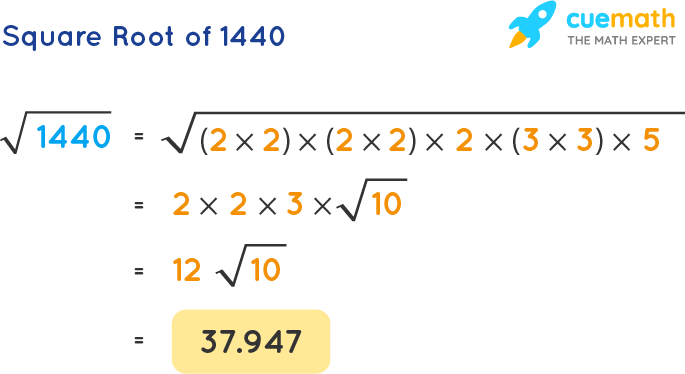Topic square root of 121: The square root of 121 is a fundamental concept in mathematics, revealing the beauty of perfect squares. Understanding how to calculate and verify the square root of 121 provides valuable insight into broader mathematical principles. In this article, we explore the definition, calculation, and significance of the square root of 121.
Table of Content
- Square Root of 121
- Introduction to Square Roots
- Understanding Perfect Squares
- Definition and Calculation of Square Root
- Calculating the Square Root of 121
- Verification of the Square Root of 121
- Properties of Square Roots
- Positive and Negative Roots
- Applications of Square Roots in Mathematics
- Common Mistakes in Finding Square Roots
- FAQs about Square Roots
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai của 121 một cách dễ hiểu và chi tiết. Phù hợp cho học sinh và người yêu thích toán học.
Square Root of 121
The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 121, the square root is:
\[
\sqrt{121} = 11
\]
Explanation
Here's a detailed explanation of how to find the square root of 121:
- 121 is a perfect square, which means it can be expressed as the product of an integer with itself.
- To find the square root of 121, we need to determine which number, when squared (multiplied by itself), equals 121.
- We can try different integers to see which one works:
- \(10 \times 10 = 100\)
- \(12 \times 12 = 144\)
- From the above, we see that \(11 \times 11 = 121\).
Properties of the Square Root of 121
Some important properties of the square root of 121 include:
- Integer Result: The square root of 121 is 11, which is an integer.
- Perfect Square: Since 121 is a perfect square, its square root is an exact integer.
- Positive and Negative Roots: While 11 is the principal (positive) square root, the negative square root of 121 is -11 because \((-11) \times (-11) = 121\).
Conclusion
The square root of 121 is \( \pm 11 \). This result indicates that both 11 and -11 are square roots of 121, with 11 being the principal square root. Understanding square roots is fundamental in mathematics, especially when dealing with quadratic equations and various algebraic expressions.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, providing insight into the properties and relationships of numbers. A square root of a number is a value that, when multiplied by itself, gives the original number. The symbol for the square root is \( \sqrt{} \).
For example, the square root of 121 is denoted as \( \sqrt{121} \). To understand square roots better, let's go through the concept step by step:
- Definition: The square root of a number \( n \) is a number \( x \) such that \( x^2 = n \).
- Perfect Squares: Numbers like 121, which have an integer as their square root, are known as perfect squares.
- Principal Square Root: The non-negative square root of a number is called the principal square root. For 121, the principal square root is 11.
- Negative Square Root: Negative numbers also have square roots. For example, the negative square root of 121 is -11 because \((-11) \times (-11) = 121\).
To find the square root of 121:
- Recognize that 121 is a perfect square.
- Determine the integer that, when squared, equals 121:
- \(10 \times 10 = 100\)
- \(11 \times 11 = 121\)
- \(12 \times 12 = 144\)
- Identify that \(11 \times 11 = 121\).
Thus, \( \sqrt{121} = 11 \). Understanding square roots is essential in various mathematical contexts, from solving equations to analyzing geometric properties.
Understanding Perfect Squares
Perfect squares are numbers that are the product of an integer multiplied by itself. They hold a significant place in mathematics due to their unique properties and the ease with which they can be identified and worked with. Let’s delve into the concept of perfect squares step by step:
- Definition: A perfect square is a number that can be expressed as \( n^2 \), where \( n \) is an integer. For example, \( 121 = 11^2 \), making 121 a perfect square.
- Properties of Perfect Squares:
- They have an odd number of total factors. For example, the factors of 121 are 1, 11, and 121.
- They always end in 0, 1, 4, 5, 6, or 9 in base 10.
- The square root of a perfect square is always an integer.
- Examples: Common perfect squares include:
- \(1^2 = 1\)
- \(2^2 = 4\)
- \(3^2 = 9\)
- \(4^2 = 16\)
- \(5^2 = 25\)
- \(10^2 = 100\)
- \(11^2 = 121\)
Identifying and working with perfect squares is straightforward. For instance, to check if a number is a perfect square, find its square root and verify if the result is an integer. In the case of 121:
- Calculate the square root: \( \sqrt{121} = 11 \).
- Since 11 is an integer, 121 is a perfect square.
Perfect squares are crucial in various areas of mathematics, including algebra, geometry, and number theory. They simplify the process of solving equations and provide insights into the properties of numbers.
Definition and Calculation of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol √. For example, the square root of 121 is written as √121.
The square root of 121 can be calculated as follows:
- Identify that 121 is a perfect square because it can be expressed as a product of an integer by itself: 121 = 11 × 11.
- Since 11 multiplied by itself equals 121, we determine that the square root of 121 is 11.
Using mathematical notation, the calculation can be expressed as:
\[ \sqrt{121} = 11 \]
This can be verified by squaring the result:
- If we take 11 and multiply it by itself: 11 × 11 = 121.
- Therefore, the square root of 121 is indeed 11.
In summary, the square root is the inverse operation of squaring a number. The calculation of the square root of 121 shows that:
\[ \sqrt{121} = 11 \]
Calculating the Square Root of 121
The square root of a number is a value that, when multiplied by itself, gives the original number. For 121, this value is 11, as 11 × 11 = 121. Here's a step-by-step guide on how to calculate the square root of 121 using different methods:
Using Prime Factorization
Prime factorization involves breaking down the number into its prime factors:
- 121 can be expressed as 11 × 11.
- Therefore, the square root of 121 is the square root of 112.
- Thus, √121 = √(112) = 11.
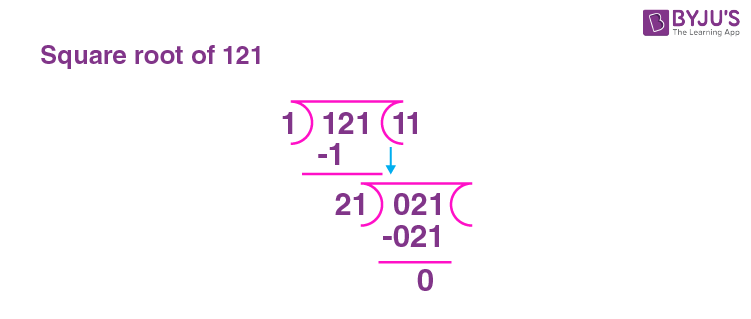
Using the Long Division Method
The long division method is a manual technique to find the square root of a number. Here are the steps:
- Write 121 as the number under the long division symbol.
- Starting from the right, divide the digits into pairs: 1 and 21.
- Find the largest number whose square is less than or equal to the first pair (1). This number is 1.
- Place the quotient (1) above the division symbol and subtract 1 from the first pair, bringing down the next pair to get 21.
- Double the quotient (1) to get 2, and find a digit (x) such that 2x multiplied by x is less than or equal to 21. This digit is 1.
- Place 1 next to the quotient, making it 11. Multiply 2 by 1 and place the result (2) under 21.
- Subtract 2 from 21 to get 19. Bring down the next pair of zeros (if continuing for decimal places) and repeat the process.
Since 121 is a perfect square, this process confirms that the square root is 11.
Using a Calculator
The simplest way to find the square root of 121 is by using a calculator:
- Enter 121 and press the square root (√) button to get the result: 11.
Using Exponentiation
In mathematical terms, the square root can be expressed using an exponent:
- √121 can be written as 1211/2.
- Therefore, 1211/2 = 11.
Verification
To verify, multiply the result by itself:
- 11 × 11 = 121.
- This confirms that the square root of 121 is indeed 11.
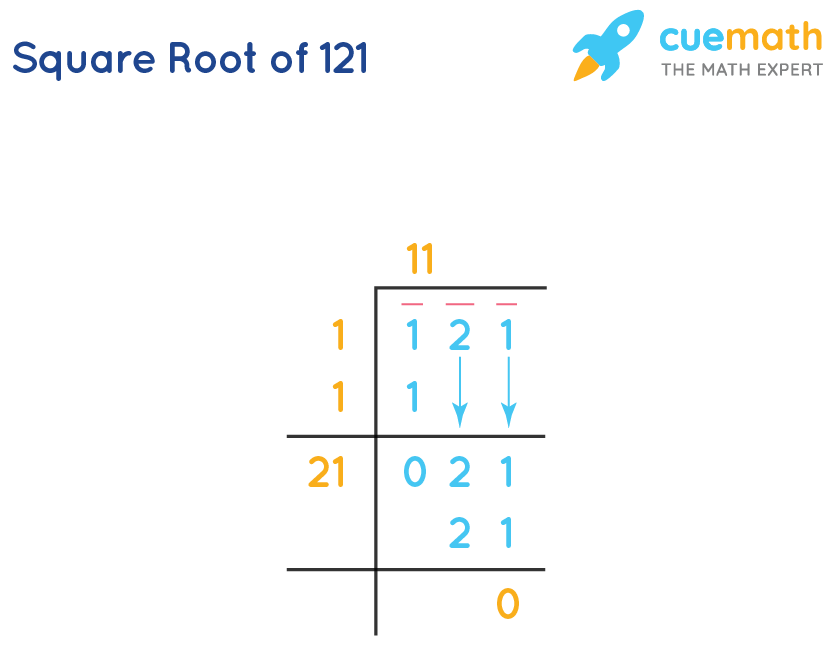
Verification of the Square Root of 121
To verify that the square root of 121 is indeed 11, we can use a couple of different methods: squaring the result and prime factorization. Let's go through these methods step-by-step.
Method 1: Squaring the Result
The most straightforward way to verify the square root of 121 is to square the result and check if it equals the original number.
- Find the square root:
\(\sqrt{121} = 11\) - Square the result:
\(11^2 = 121\) - Verify the equality: Since
11 \times 11 = 121, the square root of 121 is indeed 11.
Method 2: Prime Factorization
We can also verify the square root by using prime factorization.
- Perform prime factorization of 121:
- 121 can be expressed as \(11 \times 11\).
- Express in terms of square roots:
- \(\sqrt{121} = \sqrt{11^2}\)
- Simplify the square root:
- \(\sqrt{11^2} = 11\)
Thus, the prime factorization method confirms that the square root of 121 is 11.
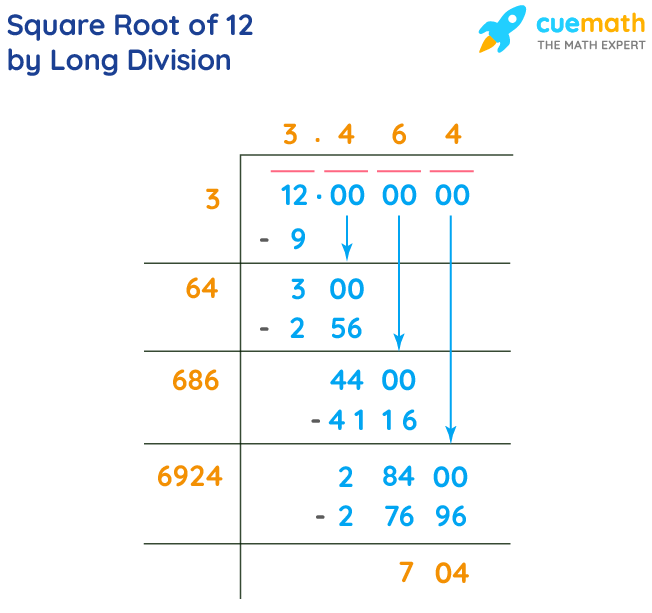
Method 3: Long Division Method
The long division method provides another way to verify the square root, particularly useful for larger numbers.
- Set up 121 for long division:
1 1 1 1 2 1 -1 0 2 1 1 1 -2 0 0 0 - Group the digits into pairs, starting from the right. For 121, we have (1)(21).
- Find the largest number whose square is less than or equal to the first pair (1):
- 1 × 1 = 1
- Subtract and bring down the next pair:
- 21 remains, and the new divisor is 2 (twice the quotient obtained).
- Find the largest digit (X) such that 2X × X ≤ 21:
- 2 × 1 = 2, 2 × 2 = 4, ..., 2 × 1 (with X = 1).
- Subtract and get the remainder as 0. The quotient 11 is the square root of 121.
Therefore, by squaring the result, using prime factorization, and applying the long division method, we can confidently verify that the square root of 121 is 11.
Properties of Square Roots
The properties of square roots are fundamental in understanding how to manipulate and simplify expressions involving square roots. Below are key properties that are essential for working with square roots:
- Product Property: The square root of a product is equal to the product of the square roots of the factors. This can be expressed as:
\[\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\]
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. This is written as:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\] \text{(where } b \neq 0\)
- Square of a Square Root: The square of a square root returns the original number:
\[(\sqrt{a})^2 = a\]
- Even and Odd Properties:
- The square root of an even perfect square is always even.
- The square root of an odd perfect square is always odd.
- Irrational Numbers: If the number inside the square root is not a perfect square, the result is an irrational number. For instance:
\[\sqrt{2} \approx 1.414213562...\]
- Negative Numbers and Imaginary Numbers: The square root of a negative number involves imaginary numbers. For example:
\[\sqrt{-1} = i\]
- Digit Restrictions: A number ending in 2, 3, 7, or 8 cannot be a perfect square, making their square roots irrational.
- Odd Number of Zeros: A number ending with an odd number of zeros is not a perfect square, thus its square root is irrational. For example:
\[\sqrt{3000} \approx 54.772255...\]
Understanding these properties helps in simplifying and calculating expressions involving square roots efficiently.
Positive and Negative Roots
In mathematics, when we talk about the square root of a number, such as the square root of 121, there are typically two solutions: one positive and one negative. Let's explore both:
- Positive Square Root: The principal (or positive) square root of 121 is denoted as \( \sqrt{121} = 11 \). This is because \( 11 \times 11 = 121 \) and \( 11 \) is a positive number.
- Negative Square Root: The negative square root of 121 is \( -11 \), represented as \( -\sqrt{121} = -11 \). This is because \( (-11) \times (-11) = 121 \) and \( -11 \) is a negative number.
Therefore, the square root of 121 has two roots: \( 11 \) and \( -11 \).
Applications of Square Roots in Mathematics
Square roots find extensive applications across various fields within mathematics. Here are some key areas where square roots are utilized:
- Geometry: In geometry, the square root function is fundamental for calculating distances, such as the length of a diagonal across a square.
- Quadratic Equations: Solving quadratic equations often involves finding square roots, especially when completing the square or using the quadratic formula.
- Statistics: Square roots are used in statistics for calculating standard deviations and other measures of variability.
- Physics: In physics, square roots appear in formulas related to energy, wave functions, and in determining magnitudes of physical quantities.
- Engineering: Engineers use square roots in various applications, such as calculating forces, stresses, and in designing structures.
- Computer Science: Square roots are essential in algorithms involving numerical methods, optimization techniques, and in cryptography.
These applications illustrate the versatility and importance of square roots in both theoretical and practical aspects of mathematics and its related disciplines.
Common Mistakes in Finding Square Roots
While finding square roots, there are common mistakes that can lead to errors. Here are some pitfalls to avoid:
- Incorrect Calculation: Carelessness in performing basic arithmetic operations, such as multiplication or addition, can result in incorrect square root values.
- Confusion with Exponents: Incorrectly applying exponent rules can lead to errors when simplifying expressions involving square roots.
- Ignoring Negative Roots: Forgetting that square roots can have both positive and negative solutions, especially in equations where both solutions are valid.
- Using Approximations: Relying solely on approximate methods without verifying using exact calculations can lead to inaccuracies.
- Not Checking Results: Failing to verify if the obtained square root satisfies the original condition or equation can lead to overlooking errors.
By being aware of these common mistakes and taking careful steps in calculations, accurate results can be achieved when finding square roots.
FAQs about Square Roots
Here are some frequently asked questions about square roots, along with their answers:
- What is a square root?
- What is the square root of 121?
- Are there both positive and negative square roots?
- What methods can be used to find the square root of 121?
- Prime Factorization Method
- Long Division Method
- Repeated Subtraction Method
- What is the prime factorization method?
- What is the long division method?
- Is the square root of 121 a rational number?
- Can square roots be decimal numbers?
- What are some common mistakes when finding square roots?
- Why are square roots important in mathematics?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 121 is 11 because 11 x 11 = 121.
The square root of 121 is 11. This can be represented as √121 = 11.
Yes, every positive number has two square roots: one positive and one negative. For 121, the square roots are 11 and -11. This is because both (11 x 11) and (-11 x -11) equal 121.
There are several methods to find the square root of 121, including:
In the prime factorization method, 121 is expressed as the product of prime numbers. Since 121 = 11 x 11, the square root of 121 is 11.
The long division method involves pairing the digits of the number and performing division in steps to find the square root. This method is particularly useful for larger numbers.
Yes, the square root of 121 is a rational number because it can be expressed as a simple fraction (11/1), which is a ratio of two integers.
Yes, square roots can be decimal numbers when the original number is not a perfect square. For example, the square root of 2 is approximately 1.414, which is an irrational number.
Common mistakes include incorrectly pairing digits in the long division method, misidentifying perfect squares, and not considering both positive and negative roots.
Square roots are important in various mathematical applications, including solving quadratic equations, geometry, and in real-world problems such as physics and engineering.
Hướng dẫn cách đơn giản hóa căn bậc hai của 121 một cách dễ hiểu và chi tiết. Phù hợp cho học sinh và người yêu thích toán học.
Cách Đơn Giản Hóa Căn Bậc Hai Của 121: sqrt(121)
READ MORE:
Tìm hiểu căn bậc hai của 121 là gì và cách tính toán đơn giản. Video giải thích chi tiết và dễ hiểu.
Căn Bậc Hai Của 121 Là Gì?