Topic what's the square root of 1/9: Understanding square roots can be fascinating, especially when dealing with fractions. In this article, we’ll explore the square root of 1/9, breaking down the calculation and its significance. Whether you’re a student, teacher, or math enthusiast, this straightforward guide will provide you with the clarity you need. Let's dive in and simplify this concept together!
Table of Content
- Square Root of 1/9
- Introduction to Square Roots
- Mathematical Definition of Square Roots
- Calculating the Square Root of 1/9
- Simplifying the Square Root of Fractions
- Square Root of 1/9: Step-by-Step Calculation
- Practical Applications of Square Roots
- Visual Representation of Square Roots
- Common Mistakes in Calculating Square Roots
- Further Reading and Resources
- YOUTUBE: Khám phá cách tính căn bậc hai của 1/9 trong video này. Hướng dẫn chi tiết và dễ hiểu giúp bạn nắm vững kiến thức toán học cơ bản.
Square Root of 1/9
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 1/9 can be calculated and understood as follows:
Calculation Steps:
- Rewrite the square root of the fraction as the division of the square roots: \(\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}}\).
- Calculate the square roots of the numerator and the denominator separately: \(\sqrt{1} = 1\) and \(\sqrt{9} = 3\).
- Divide the results: \(\frac{1}{3}\).
Therefore, the square root of \(\frac{1}{9}\) is \(\frac{1}{3}\).
Mathematical Representation:
\[\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}\]
Properties of Square Roots:
- Every nonnegative real number \(a\) has a unique nonnegative square root, called the principal square root, denoted as \(\sqrt{a}\).
- The square root of a fraction can be found by taking the square root of the numerator and the denominator separately.
- The principal square root of a perfect square is an integer.
Examples:
| Example | Calculation | Result |
|---|---|---|
| Square root of 4 | \(\sqrt{4} = 2\) | 2 |
| Square root of 16 | \(\sqrt{16} = 4\) | 4 |
| Square root of 25 | \(\sqrt{25} = 5\) | 5 |
For more detailed information, you can use online calculators and resources such as Mathway, Symbolab, Math.net, Microsoft Math Solver, and Byju's to explore and verify square root calculations and other mathematical operations.

READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing a number that, when multiplied by itself, yields the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\). The square root symbol is denoted as \(\sqrt{}\).
When dealing with fractions, the concept remains the same. The square root of a fraction involves finding a number which, when squared, gives the original fraction. For instance, finding the square root of \(\frac{1}{9}\) requires a few straightforward steps:
- Identify the numerator and denominator of the fraction. In this case, the numerator is 1 and the denominator is 9.
- Find the square root of the numerator. The square root of 1 is 1 because \(1 \times 1 = 1\).
- Find the square root of the denominator. The square root of 9 is 3 because \(3 \times 3 = 9\).
- Combine these results to form the square root of the fraction. Thus, the square root of \(\frac{1}{9}\) is \(\frac{1}{3}\).
In mathematical notation, this can be represented as:
\[
\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}
\]
Square roots have practical applications in various fields such as engineering, physics, and finance, making them an essential part of the mathematical toolkit. Understanding how to simplify and calculate square roots, especially with fractions, can enhance problem-solving skills and mathematical comprehension.
Mathematical Definition of Square Roots
The square root of a number is a value that, when multiplied by itself, yields the original number. Mathematically, if \(x\) is the square root of \(y\), then:
\[
x^2 = y
\]
This can also be written using the square root symbol \(\sqrt{}\), where:
\[
x = \sqrt{y}
\]
For example, since \(3^2 = 9\), it follows that:
\[
3 = \sqrt{9}
\]
Square roots apply to both whole numbers and fractions. When dealing with fractions, the process involves finding the square root of both the numerator and the denominator separately. The square root of a fraction \(\frac{a}{b}\) is given by:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
To illustrate, let's find the square root of \(\frac{1}{9}\):
- Identify the numerator (1) and the denominator (9).
- Calculate the square root of the numerator: \(\sqrt{1} = 1\).
- Calculate the square root of the denominator: \(\sqrt{9} = 3\).
- Combine these results to form the square root of the fraction: \(\frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}\).
Thus, the square root of \(\frac{1}{9}\) is \(\frac{1}{3}\), and in mathematical terms:
\[
\sqrt{\frac{1}{9}} = \frac{1}{3}
\]
This process of finding the square root is fundamental in mathematics and is used in various applications such as solving quadratic equations, geometry, and in the analysis of scientific data.
Calculating the Square Root of 1/9
Calculating the square root of a fraction such as \(\frac{1}{9}\) involves a few straightforward steps. Here, we will walk through the process in detail:
- Identify the Fraction:
First, recognize that the fraction in question is \(\frac{1}{9}\). This fraction consists of a numerator (1) and a denominator (9).
- Calculate the Square Root of the Numerator:
The square root of the numerator, which is 1, needs to be determined. Since \(1 \times 1 = 1\), we have:
\[
\sqrt{1} = 1
\] - Calculate the Square Root of the Denominator:
Next, find the square root of the denominator, which is 9. Since \(3 \times 3 = 9\), we get:
\[
\sqrt{9} = 3
\] - Combine the Results:
Combine the square roots of the numerator and the denominator to form the square root of the fraction. This gives us:
\[
\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}
\]
Therefore, the square root of \(\frac{1}{9}\) is \(\frac{1}{3}\). This calculation can be confirmed by squaring the result to see if we return to the original fraction:
\[
\left(\frac{1}{3}\right)^2 = \frac{1^2}{3^2} = \frac{1}{9}
\]
This step-by-step method ensures that you can accurately find the square root of any fraction by separately determining the square roots of the numerator and the denominator, then combining these results. Understanding this process is valuable for solving a wide range of mathematical problems involving fractions.
Simplifying the Square Root of Fractions
Simplifying the square root of fractions involves breaking down the fraction into its numerator and denominator and then finding the square root of each component separately. This process can be performed step by step as follows:
- Identify the Fraction:
Consider a fraction \(\frac{a}{b}\) where both \(a\) and \(b\) are positive integers. For this example, we use \(\frac{1}{9}\).
- Separate the Numerator and Denominator:
Write the fraction under a single square root as the quotient of two square roots:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]For \(\frac{1}{9}\), this becomes:
\[
\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}}
\] - Calculate the Square Root of the Numerator:
Find the square root of the numerator \(a\). Since \(a = 1\), we have:
\[
\sqrt{1} = 1
\] - Calculate the Square Root of the Denominator:
Next, find the square root of the denominator \(b\). Since \(b = 9\), we get:
\[
\sqrt{9} = 3
\] - Combine the Results:
Put the square roots of the numerator and the denominator back together:
\[
\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}
\]
Thus, the square root of \(\frac{1}{9}\) simplifies to \(\frac{1}{3}\). This method of simplification can be applied to any fraction, ensuring a clear and accurate calculation. Simplifying square roots of fractions is a useful skill in algebra, geometry, and other areas of mathematics, aiding in solving equations and understanding mathematical relationships more deeply.

Square Root of 1/9: Step-by-Step Calculation
Calculating the square root of \(\frac{1}{9}\) involves a few clear and simple steps. Here, we will walk through the process in detail:
- Understand the Problem:
The goal is to find the square root of the fraction \(\frac{1}{9}\). This means we need a number that, when multiplied by itself, equals \(\frac{1}{9}\).
- Express the Fraction Under a Single Square Root:
Start by writing the fraction under a single square root:
\[
\sqrt{\frac{1}{9}}
\] - Separate the Numerator and Denominator:
Utilize the property of square roots that allows us to split the fraction into two separate square roots:
\[
\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}}
\] - Calculate the Square Root of the Numerator:
Find the square root of the numerator (1). Since \(1 \times 1 = 1\), we have:
\[
\sqrt{1} = 1
\] - Calculate the Square Root of the Denominator:
Find the square root of the denominator (9). Since \(3 \times 3 = 9\), we get:
\[
\sqrt{9} = 3
\] - Combine the Results:
Combine the square roots of the numerator and the denominator to form the square root of the fraction:
\[
\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}
\] - Verify the Result:
To confirm, we can square the result to check if we return to the original fraction:
\[
\left(\frac{1}{3}\right)^2 = \frac{1^2}{3^2} = \frac{1}{9}
\]The calculation is correct.
By following these steps, you can accurately determine that the square root of \(\frac{1}{9}\) is \(\frac{1}{3}\). This step-by-step approach ensures clarity and precision in your calculations, making it easier to handle similar problems involving the square roots of fractions.
Practical Applications of Square Roots
Square roots are fundamental in various fields of science, engineering, and everyday life. Here are some practical applications where understanding and using square roots is essential:
- Geometry and Trigonometry:
Square roots are crucial in calculating distances and lengths in geometric shapes. For example, the Pythagorean theorem uses square roots to determine the length of the hypotenuse in a right triangle:
\[
c = \sqrt{a^2 + b^2}
\]This formula helps in architectural design, construction, and various engineering applications.
- Physics and Engineering:
In physics, square roots are used to solve equations involving motion, energy, and waves. For instance, the formula for calculating the period of a pendulum involves a square root:
\[
T = 2\pi \sqrt{\frac{L}{g}}
\]where \(T\) is the period, \(L\) is the length of the pendulum, and \(g\) is the acceleration due to gravity.
- Statistics and Probability:
Square roots are used in statistics to calculate standard deviation, which measures the amount of variation or dispersion in a set of values:
\[
\sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2}
\]where \(\sigma\) is the standard deviation, \(N\) is the number of observations, \(x_i\) are the values, and \(\mu\) is the mean.
- Finance and Economics:
In finance, square roots are used to calculate the volatility of stock prices and to model risk and return. For example, the square root of time is used in the calculation of the standard deviation of returns over a given period:
\[
\sigma_{t} = \sigma_{\text{daily}} \sqrt{t}
\]where \(\sigma_{t}\) is the standard deviation over time \(t\) and \(\sigma_{\text{daily}}\) is the daily standard deviation.
- Computer Science:
In computer graphics, square roots are used in algorithms for rendering images, calculating distances between points, and normalizing vectors. Efficient computation of square roots is important for performance in 3D graphics and simulations.
Understanding square roots and their applications helps in solving real-world problems across various disciplines, enhancing analytical and problem-solving skills.
Visual Representation of Square Roots
Visualizing square roots can provide a deeper understanding of their meaning and how they function in mathematics. Here, we explore different ways to represent square roots, including geometric and graphical methods.
Geometric Representation
One common method to visualize square roots is through geometry. For instance, consider a square with an area of 1 square unit. The side length of this square is the square root of the area. In this case, the side length is:
\[
\sqrt{1} = 1
\]
Similarly, for a square with an area of 9 square units, the side length is:
\[
\sqrt{9} = 3
\]
For the fraction \(\frac{1}{9}\), imagine a smaller square with an area of \(\frac{1}{9}\) square units. The side length of this smaller square is:
\[
\sqrt{\frac{1}{9}} = \frac{1}{3}
\]
Graphical Representation
Graphing functions can also help visualize square roots. The function \(y = \sqrt{x}\) represents the square root of \(x\) on a Cartesian plane. Here’s a step-by-step approach to graphing this function:
- Plot Key Points:
Identify key points where the function \(y = \sqrt{x}\) has simple, known values. For example:
- When \(x = 0\), \(y = \sqrt{0} = 0\).
- When \(x = 1\), \(y = \sqrt{1} = 1\).
- When \(x = 4\), \(y = \sqrt{4} = 2\).
- When \(x = 9\), \(y = \sqrt{9} = 3\).
- Draw the Curve:
Connect these points with a smooth curve to represent the function \(y = \sqrt{x}\). The curve will start at the origin (0,0) and increase gradually, illustrating how the square root function grows.
The graph below represents the square root function:
\[
\begin{array}{c|c}
x & y = \sqrt{x} \\
\hline
0 & 0 \\
1 & 1 \\
4 & 2 \\
9 & 3 \\
\end{array}
\]
Number Line Representation
Another way to visualize square roots is on a number line. Plotting \(\sqrt{1}\), \(\sqrt{4}\), \(\sqrt{9}\), and \(\sqrt{\frac{1}{9}}\) on a number line helps in understanding their relative positions and magnitudes. For example, \(\frac{1}{3}\) is smaller than 1, indicating that \(\sqrt{\frac{1}{9}}\) is less than \(\sqrt{1}\).
These visual tools provide a clearer picture of square roots, enhancing comprehension and application in various mathematical contexts.
Common Mistakes in Calculating Square Roots
Calculating square roots, particularly of fractions, can sometimes lead to mistakes. Here are some common errors to watch out for and how to avoid them:
- Forgetting the Definition: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). For fractions, this means finding a number which, when squared, equals the fraction.
- Ignoring Simplification: Simplify the fraction first if possible. For example, \( \sqrt{\frac{4}{9}} \) can be simplified to \( \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3} \).
- Incorrect Application of Square Root to Numerator and Denominator: When dealing with fractions, apply the square root to both the numerator and the denominator separately. For instance, \( \sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3} \).
- Sign Confusion: Remember that both positive and negative numbers can be square roots (e.g., both \( \frac{1}{3} \) and \( -\frac{1}{3} \) are square roots of \( \frac{1}{9} \)). However, in many contexts, the principal (positive) root is used.
- Mistaking Square Root for Division: Do not confuse finding the square root of a fraction with dividing by 2. For example, \( \sqrt{\frac{1}{9}} \neq \frac{1}{9} \div 2 \).
- Using Incorrect Values: Ensure the values used in calculations are accurate. For instance, knowing that \( \sqrt{9} = 3 \) is essential to accurately find \( \sqrt{\frac{1}{9}} \).
To avoid these mistakes, follow these steps:
- Identify the fraction you need the square root of, e.g., \( \frac{1}{9} \).
- Apply the square root to the numerator and the denominator separately: \( \sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} \).
- Calculate the square roots: \( \sqrt{1} = 1 \) and \( \sqrt{9} = 3 \).
- Combine the results to get the final answer: \( \frac{1}{3} \).
By following these steps and being mindful of common mistakes, you can accurately calculate the square roots of fractions like \( \frac{1}{9} \).
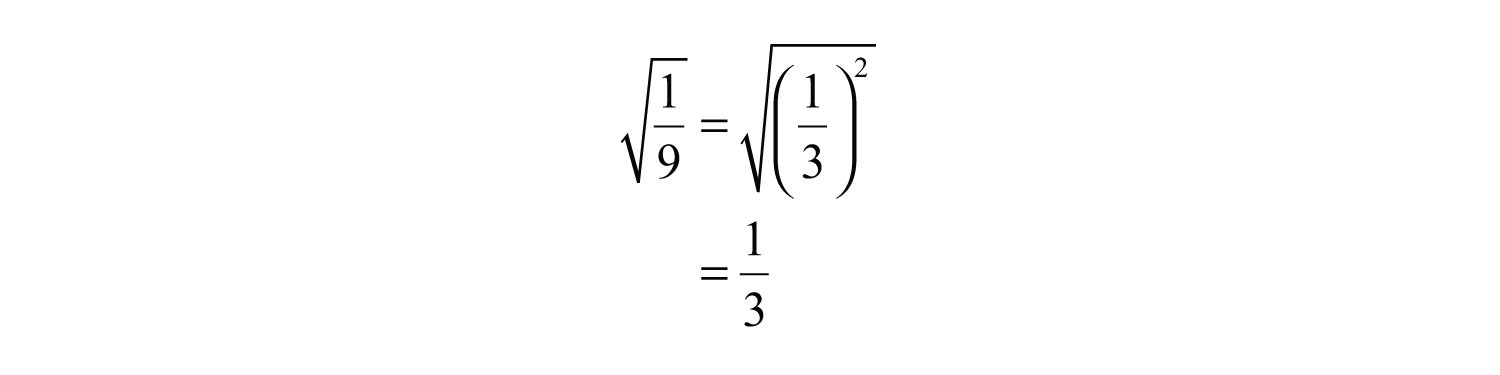
Further Reading and Resources
To deepen your understanding of square roots, particularly the square root of fractions like 1/9, the following resources will be helpful:
-
This resource provides a step-by-step explanation of how to simplify the square root of 1/9, including separating the square root of the numerator and the denominator.
-
Learn about the principal square root, the notation, and use the interactive calculator to explore square roots of various numbers.
-
Explore detailed explanations and community answers on how to simplify the square root of 1/9, including various mathematical properties and methods.
-
Discover intuitive explanations and visual aids to understand squares and square roots, including practical methods to calculate them manually.
These resources will not only help you understand the square root of 1/9 but also provide broader insights into the concept of square roots and their applications in different mathematical contexts.
Khám phá cách tính căn bậc hai của 1/9 trong video này. Hướng dẫn chi tiết và dễ hiểu giúp bạn nắm vững kiến thức toán học cơ bản.
Căn bậc hai của 1/9 | Root(1/9)
READ MORE:
Tìm hiểu cách rút gọn căn bậc hai của 1/9 trong video này. Hướng dẫn chi tiết và dễ hiểu giúp bạn nắm vững kiến thức toán học cơ bản.
Rút gọn căn bậc hai của 1/9, căn bậc hai của 1/9