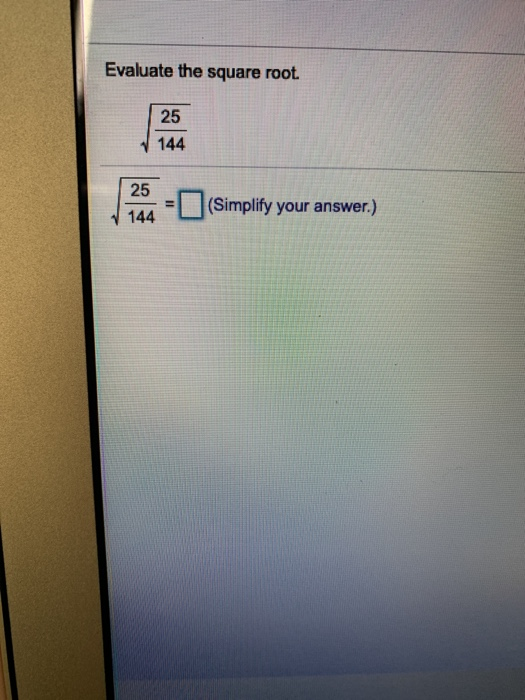
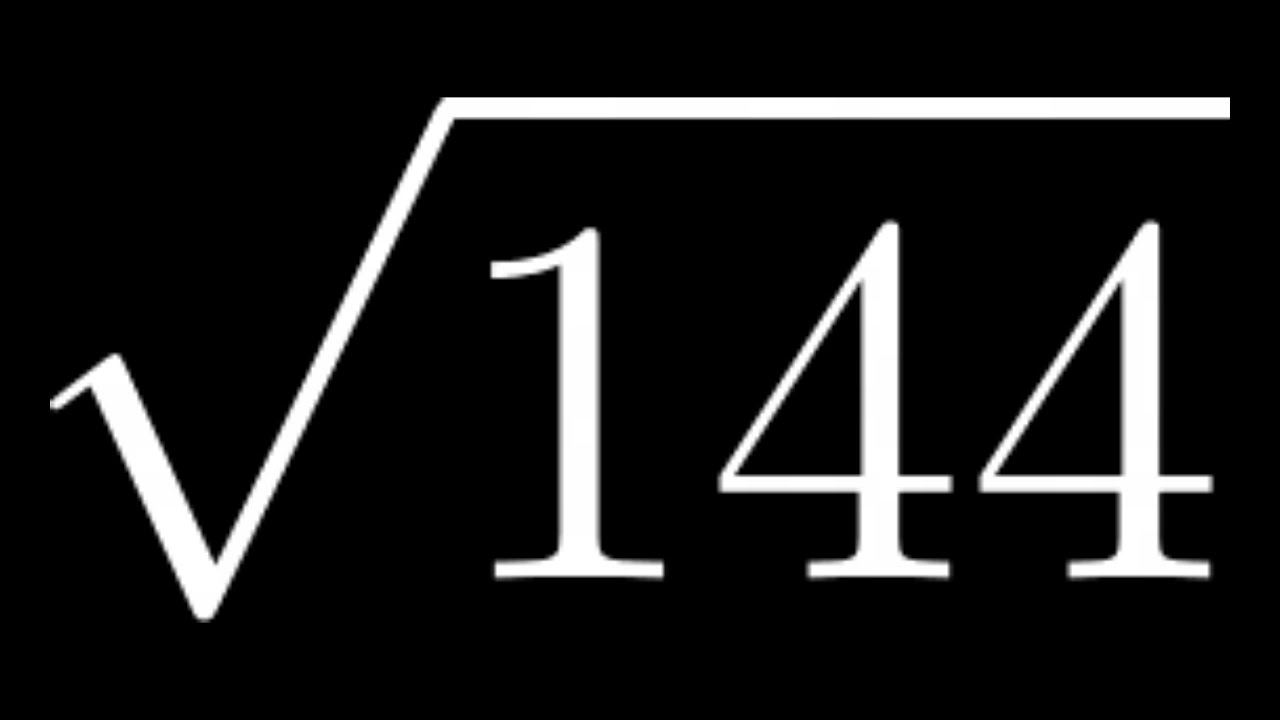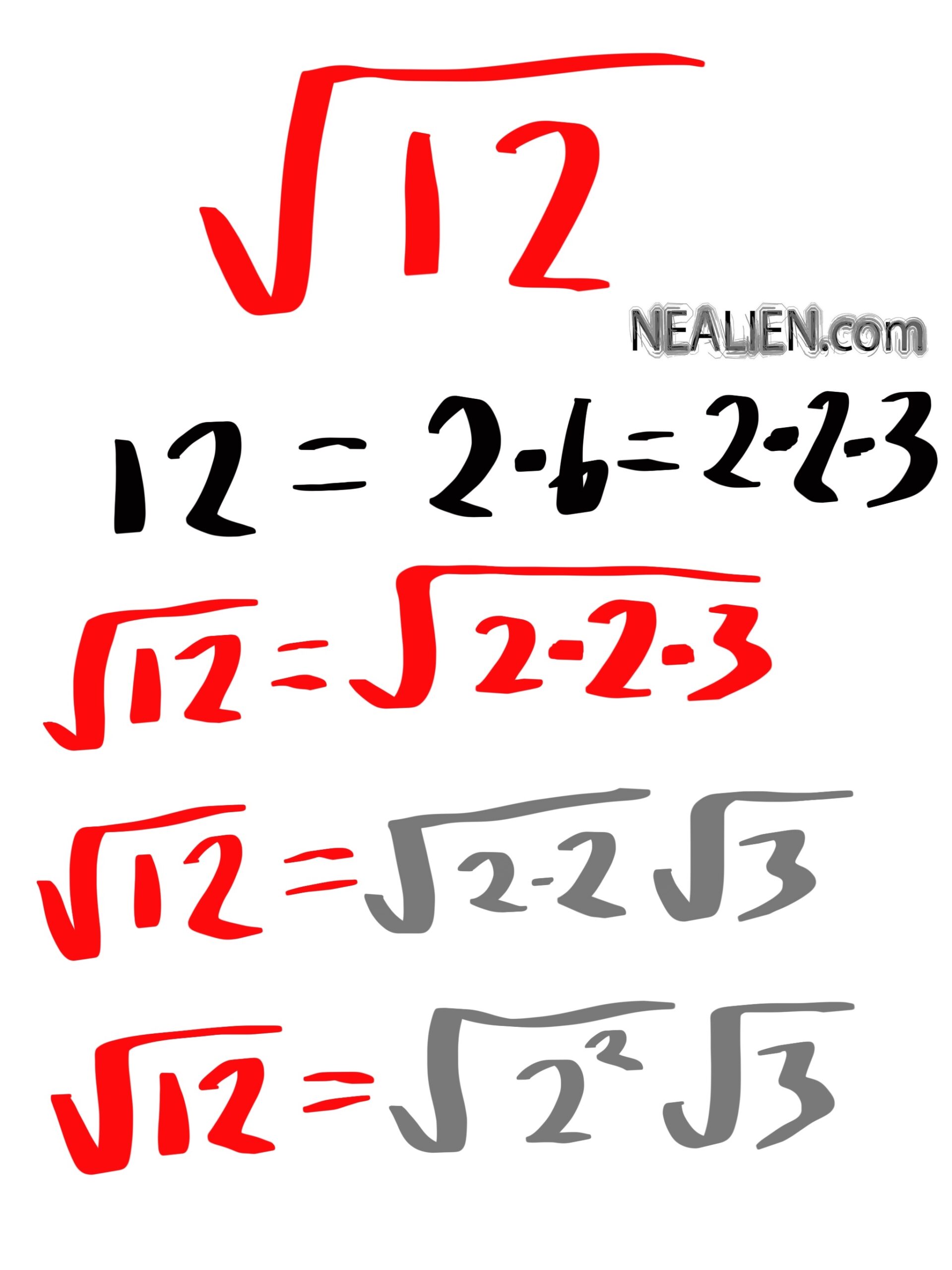Topic square root of 25/144: The square root of 25/144 may seem daunting at first, but with a step-by-step approach, it becomes easy to understand and calculate. In this article, we'll break down the process, simplify the fraction, and explore its significance in practical applications, making it accessible and engaging for learners of all levels.
Table of Content
- Understanding the Square Root of 144
- Introduction to Square Roots
- Basics of Fractions and Rational Numbers
- Square Root Calculation: Step-by-Step Guide
- Understanding Perfect Squares
- Breaking Down the Fraction: 25/144
- Square Root of Numerator: √25
- Square Root of Denominator: √144
- Combining the Square Roots: √(25/144)
- Simplifying Square Roots
- Decimal Approximation of √(25/144)
- Visual Representation of √(25/144)
- Applications of Square Roots in Real Life
- Common Mistakes and How to Avoid Them
- Practice Problems and Solutions
- Further Reading and Resources
- YOUTUBE: Xem video để học cách đơn giản hóa biểu thức với căn bậc hai “√(25) + √(144)” qua từng bước giải đại số. Phù hợp cho người học toán.
Understanding the Square Root of 144
The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 144, the square root is:
$$\sqrt{144} = 12$$
Why is the Square Root of 144 Equal to 12?
The square root of 144 equals 12 because:
- When 12 is multiplied by itself, the result is 144.
- Mathematically, this can be expressed as \( 12 \times 12 = 144 \).
Calculation Steps
- Identify the number: \(144\).
- Determine the number whose square equals \(144\).
- The solution is \( \sqrt{144} = 12 \).
Verification
To verify the result, you can multiply the square root by itself:
Since the product is equal to 144, our calculation is correct.
Properties of the Square Root of 144
- Perfect Square: 144 is a perfect square, meaning its square root is a whole number.
- Positive and Negative Roots: While the principal square root is positive (12), there is also a negative square root: -12. Thus, both \( \sqrt{144} = 12 \) and \( \sqrt{144} = -12 \).
- Applications: The square root of 144 is commonly used in various mathematical and real-life applications, such as geometry and algebra.
Representation in Different Forms
The square root of 144 can also be represented in exponential form as:
\( 144^{0.5} = 12 \)
Or in radical form:
Conclusion
Understanding the square root of 144 and its properties helps in grasping fundamental concepts in mathematics. Knowing that \( \sqrt{144} = 12 \) enables easier calculation and application in various problems.
READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics that involve finding a number which, when multiplied by itself, yields the original number. They are essential in various fields, including algebra, geometry, and real-life applications. Here's a detailed introduction to understanding square roots:
The square root of a number \( x \) is denoted as \( \sqrt{x} \). For instance, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
Basic Properties of Square Roots
- Non-negative Numbers: The square root of a non-negative number is always non-negative.
- Product Rule: The square root of a product is the product of the square roots. \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
- Quotient Rule: The square root of a quotient is the quotient of the square roots. \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25, whose square roots are integers, are called perfect squares.
Calculating Square Roots
To calculate the square root of a fraction, such as \( \frac{25}{144} \), follow these steps:
- Find the square root of the numerator: \( \sqrt{25} = 5 \).
- Find the square root of the denominator: \( \sqrt{144} = 12 \).
- Combine the results: \( \sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}} = \frac{5}{12} \).
Understanding and Using Square Roots
Square roots are not only theoretical concepts but also practical tools used in various scenarios such as:
- Geometry: Calculating the side length of a square given its area.
- Physics: Understanding relationships involving energy, force, and distances.
- Finance: Computing compound interest and growth rates.
With a solid understanding of square roots, you can tackle more complex mathematical problems and appreciate their applications in everyday life.
Basics of Fractions and Rational Numbers
Fractions and rational numbers are core components of mathematics that are used to represent parts of a whole and ratios between numbers. Understanding these concepts is essential for working with square roots of fractions, such as \( \frac{25}{144} \). Let's explore these basics in detail:
Definition of Fractions
A fraction consists of two parts: a numerator and a denominator. The numerator represents the number of parts we have, while the denominator represents the total number of equal parts the whole is divided into. For example, in the fraction \( \frac{3}{4} \), 3 is the numerator, and 4 is the denominator.
Types of Fractions
- Proper Fractions: The numerator is less than the denominator (e.g., \( \frac{3}{4} \)).
- Improper Fractions: The numerator is greater than or equal to the denominator (e.g., \( \frac{5}{4} \)).
- Mixed Numbers: A combination of a whole number and a proper fraction (e.g., \( 1 \frac{1}{2} \)).
Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction \( \frac{p}{q} \) of two integers, where \( p \) (the numerator) and \( q \) (the denominator) are integers, and \( q \) is not zero. This includes all fractions, integers, and finite decimals.
Simplifying Fractions
To simplify a fraction, divide the numerator and the denominator by their greatest common divisor (GCD). For instance, to simplify \( \frac{25}{100} \):
- Find the GCD of 25 and 100, which is 25.
- Divide both the numerator and the denominator by the GCD: \[ \frac{25 \div 25}{100 \div 25} = \frac{1}{4} \]
Equivalent Fractions
Fractions that represent the same value are called equivalent fractions. For example, \( \frac{2}{4} \), \( \frac{3}{6} \), and \( \frac{1}{2} \) are equivalent because they all simplify to \( \frac{1}{2} \).
Operations with Fractions
- Addition/Subtraction: To add or subtract fractions, make sure they have a common denominator, then add or subtract the numerators. \[ \frac{1}{4} + \frac{1}{4} = \frac{1+1}{4} = \frac{2}{4} = \frac{1}{2} \]
- Multiplication: Multiply the numerators together and the denominators together. \[ \frac{2}{3} \times \frac{4}{5} = \frac{2 \times 4}{3 \times 5} = \frac{8}{15} \]
- Division: Invert the second fraction (reciprocal) and multiply. \[ \frac{2}{3} \div \frac{4}{5} = \frac{2}{3} \times \frac{5}{4} = \frac{2 \times 5}{3 \times 4} = \frac{10}{12} = \frac{5}{6} \]
Applying Fractions and Rational Numbers
Understanding fractions and rational numbers is crucial for solving real-world problems, including those involving ratios, proportions, and rates. They are used in various fields such as cooking, construction, finance, and science.
By mastering these basic concepts, you can confidently tackle more complex mathematical challenges, including the calculation of square roots of fractions like \( \frac{25}{144} \).
Square Root Calculation: Step-by-Step Guide
Calculating the square root of a fraction, such as \( \frac{25}{144} \), can be simplified by following a clear, step-by-step process. This guide will walk you through each step to ensure a thorough understanding.
Step 1: Understand the Fraction
Identify the numerator and the denominator of the fraction \( \frac{25}{144} \). Here, 25 is the numerator, and 144 is the denominator.
Step 2: Find the Square Root of the Numerator
Calculate the square root of the numerator (25):
\[
\sqrt{25} = 5
\]
Since 25 is a perfect square, its square root is 5.
Step 3: Find the Square Root of the Denominator
Calculate the square root of the denominator (144):
\[
\sqrt{144} = 12
\]
Similarly, 144 is a perfect square, and its square root is 12.
Step 4: Combine the Results
Combine the square roots of the numerator and the denominator to find the square root of the fraction:
\[
\sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}} = \frac{5}{12}
\]
Step 5: Simplify (if needed)
In this case, the fraction \( \frac{5}{12} \) is already in its simplest form. If the fraction were not simplified, you would need to find the greatest common divisor (GCD) of the numerator and the denominator and divide both by this number.
Additional Example for Practice
To further illustrate the process, consider another fraction \( \frac{16}{81} \):
- Find the square root of the numerator: \[ \sqrt{16} = 4 \]
- Find the square root of the denominator: \[ \sqrt{81} = 9 \]
- Combine the results: \[ \sqrt{\frac{16}{81}} = \frac{4}{9} \]
Understanding the Result
The square root of \( \frac{25}{144} \) is \( \frac{5}{12} \), which means if you square \( \frac{5}{12} \), you will get \( \frac{25}{144} \):
\[
\left(\frac{5}{12}\right)^2 = \frac{5^2}{12^2} = \frac{25}{144}
\]
By following these steps, you can confidently calculate the square root of any fraction, simplifying the process and ensuring accuracy.
Understanding Perfect Squares
Perfect squares are numbers that are the squares of integers. They play a crucial role in simplifying square roots and understanding mathematical relationships. This section delves into the concept of perfect squares, providing detailed insights and examples.
Definition of Perfect Squares
A perfect square is a number that can be expressed as the product of an integer with itself. For example, \( n \) is a perfect square if there exists an integer \( m \) such that:
\[
n = m \times m = m^2
\]
Examples of perfect squares include 1, 4, 9, 16, 25, 36, and so on.
Properties of Perfect Squares
- Non-negative: All perfect squares are non-negative since they result from multiplying an integer by itself.
- Odd and Even: The square of an even number is even, and the square of an odd number is odd.
- Digit Patterns: Perfect squares end in specific digits (0, 1, 4, 5, 6, or 9 in base 10).
Identifying Perfect Squares
To determine if a number is a perfect square, find its square root and check if the result is an integer. For instance:
\[
\sqrt{25} = 5 \quad \text{(5 is an integer, so 25 is a perfect square)}
\]
\[
\sqrt{26} \approx 5.099 \quad \text{(not an integer, so 26 is not a perfect square)}
\]
List of Common Perfect Squares
| 1 | \(1^2\) |
| 4 | \(2^2\) |
| 9 | \(3^2\) |
| 16 | \(4^2\) |
| 25 | \(5^2\) |
| 36 | \(6^2\) |
| 49 | \(7^2\) |
| 64 | \(8^2\) |
| 81 | \(9^2\) |
| 100 | \(10^2\) |
Importance in Simplifying Square Roots
Perfect squares are particularly useful when simplifying square roots. For example, knowing that 25 and 144 are perfect squares helps simplify \( \sqrt{\frac{25}{144}} \):
\[
\sqrt{25} = 5 \quad \text{and} \quad \sqrt{144} = 12
\]
Therefore:
\[
\sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}} = \frac{5}{12}
\]
Practical Applications of Perfect Squares
- Geometry: Calculating areas of squares and rectangles.
- Algebra: Solving quadratic equations and simplifying expressions.
- Engineering: Determining dimensions and optimizing designs.
Understanding perfect squares is fundamental to many areas of mathematics and practical problem-solving. Recognizing and working with perfect squares simplifies complex calculations and enhances mathematical fluency.

Breaking Down the Fraction: 25/144
The fraction \( \frac{25}{144} \) can be understood and simplified by examining its components and mathematical properties. This section will break down the fraction step by step to provide a clear understanding.
Numerator and Denominator
In the fraction \( \frac{25}{144} \), the numerator is 25, and the denominator is 144. Both numbers are perfect squares, which simplifies the process of finding their square roots.
Prime Factorization
One way to understand fractions better is through prime factorization. Here, we find the prime factors of both the numerator and the denominator:
- Prime factors of 25: \[ 25 = 5 \times 5 = 5^2 \]
- Prime factors of 144: \[ 144 = 12 \times 12 = (2 \times 6) \times (2 \times 6) = (2^2 \times 3) \times (2^2 \times 3) = 2^4 \times 3^2 \]
Perfect Squares
Recognizing that both the numerator and the denominator are perfect squares:
\[
25 = 5^2 \quad \text{and} \quad 144 = 12^2
\]
This allows us to simplify the square root calculation.
Simplifying the Fraction
Since 25 and 144 are perfect squares, we can simplify \( \frac{25}{144} \) by taking the square root of both the numerator and the denominator:
- Find the square root of 25: \[ \sqrt{25} = 5 \]
- Find the square root of 144: \[ \sqrt{144} = 12 \]
- Combine the results: \[ \sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}} = \frac{5}{12} \]
Verifying the Result
To ensure the fraction is simplified correctly, you can verify by squaring the simplified result:
\[
\left(\frac{5}{12}\right)^2 = \frac{5^2}{12^2} = \frac{25}{144}
\]
This confirms that \( \frac{5}{12} \) is indeed the square root of \( \frac{25}{144} \).
Applications of the Simplified Fraction
- Mathematical Problems: Simplified fractions are easier to use in algebraic equations and other mathematical problems.
- Practical Applications: In fields like engineering and physics, simplified fractions help in making precise calculations and measurements.
Breaking down the fraction \( \frac{25}{144} \) and understanding its components not only simplifies calculations but also enhances comprehension of the mathematical concepts involved.
Square Root of Numerator: √25
Calculating the square root of the numerator, 25, is a straightforward process since 25 is a perfect square. This section will guide you through the steps to understand and calculate \( \sqrt{25} \).
Understanding Perfect Squares
A perfect square is a number that can be expressed as the product of an integer with itself. In this case, 25 is a perfect square because it can be written as:
\[
25 = 5 \times 5 = 5^2
\]
Calculating the Square Root
The square root of a number is the value that, when multiplied by itself, gives the original number. For 25:
\[
\sqrt{25} = 5
\]
This is because:
\[
5 \times 5 = 25
\]
Step-by-Step Calculation
Here are the steps to calculate the square root of 25:
- Identify the number: In this case, the number is 25.
- Check if the number is a perfect square: Since 25 can be written as \( 5^2 \), it is a perfect square.
- Find the integer value: Determine the integer whose square is 25. This integer is 5. \[ \sqrt{25} = 5 \]
Verification
To verify the calculation, square the result to see if you get the original number:
\[
5 \times 5 = 25
\]
Since the calculation holds true, \( \sqrt{25} = 5 \) is correct.
Applications of √25
- Geometry: In geometry, the square root is used to determine the side length of a square given its area. For instance, a square with an area of 25 square units has a side length of 5 units.
- Algebra: The square root function is fundamental in solving quadratic equations and simplifying expressions.
- Real-Life Scenarios: Understanding square roots can help in various practical scenarios, such as calculating distances, areas, and in financial mathematics.
By understanding and calculating the square root of 25, you gain a deeper appreciation of how perfect squares and their roots function in both theoretical and practical applications.
Square Root of Denominator: √144
The denominator of the fraction \( \frac{25}{144} \) is 144. Calculating the square root of 144 is straightforward because 144 is a perfect square. This section will provide a detailed, step-by-step guide to understanding and calculating \( \sqrt{144} \).
Understanding Perfect Squares
A perfect square is a number that can be expressed as the product of an integer with itself. In this case, 144 is a perfect square because it can be written as:
\[
144 = 12 \times 12 = 12^2
\]
Calculating the Square Root
The square root of a number is the value that, when multiplied by itself, gives the original number. For 144:
\[
\sqrt{144} = 12
\]
This is because:
\[
12 \times 12 = 144
\]
Step-by-Step Calculation
Here are the steps to calculate the square root of 144:
- Identify the number: In this case, the number is 144.
- Check if the number is a perfect square: Since 144 can be written as \( 12^2 \), it is a perfect square.
- Find the integer value: Determine the integer whose square is 144. This integer is 12. \[ \sqrt{144} = 12 \]
Verification
To verify the calculation, square the result to see if you get the original number:
\[
12 \times 12 = 144
\]
Since the calculation holds true, \( \sqrt{144} = 12 \) is correct.
Prime Factorization Method
Another way to understand the square root is through prime factorization:
\ul>
Applications of √144
- Geometry: In geometry, the square root is used to determine the side length of a square given its area. For instance, a square with an area of 144 square units has a side length of 12 units.
- Algebra: The square root function is fundamental in solving quadratic equations and simplifying expressions.
- Real-Life Scenarios: Understanding square roots can help in various practical scenarios, such as calculating distances, areas, and in financial mathematics.
By understanding and calculating the square root of 144, you gain a deeper appreciation of how perfect squares and their roots function in both theoretical and practical applications.
Combining the Square Roots: √(25/144)
Combining the square roots of the numerator and the denominator of the fraction \( \frac{25}{144} \) involves calculating the square root of the entire fraction. This section will provide a detailed, step-by-step guide to understanding and calculating \( \sqrt{\frac{25}{144}} \).
Square Root of a Fraction
The square root of a fraction can be determined by taking the square root of the numerator and the square root of the denominator separately:
\[
\sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}}
\]
Step-by-Step Calculation
Here are the steps to calculate \( \sqrt{\frac{25}{144}} \):
- Identify the numerator and denominator: The numerator is 25, and the denominator is 144.
- Calculate the square root of the numerator: \[ \sqrt{25} = 5 \]
- Calculate the square root of the denominator: \[ \sqrt{144} = 12 \]
- Combine the results: Place the square roots of the numerator and denominator into the fraction: \[ \sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}} = \frac{5}{12} \]
Verification
To ensure the calculation is correct, square the result to see if you get the original fraction:
\[
\left(\frac{5}{12}\right)^2 = \frac{5^2}{12^2} = \frac{25}{144}
\]
Since the calculation holds true, \( \sqrt{\frac{25}{144}} = \frac{5}{12} \) is correct.
Applications of Square Root of a Fraction
- Mathematical Problems: Simplifying fractions and solving algebraic equations often require finding the square root of a fraction.
- Geometry: Determining dimensions and areas in geometric problems can involve square roots of fractions.
- Real-Life Scenarios: Practical applications in engineering, physics, and finance often involve square roots of fractions for precise calculations.
Visualization
Visualizing the process can help in understanding the concept. Consider a square with an area of \( \frac{25}{144} \) square units. The side length of this square would be:
\[
\sqrt{\frac{25}{144}} = \frac{5}{12} \text{ units}
\]
By breaking down the fraction \( \frac{25}{144} \) into its numerator and denominator, and calculating the square root of each separately, you can easily find the square root of the entire fraction. This method simplifies complex fractions and enhances your mathematical problem-solving skills.

Simplifying Square Roots
Understanding how to simplify square roots is essential in mathematics. Simplifying the square root of a fraction, such as \( \sqrt{\frac{25}{144}} \), involves a few straightforward steps. Here's a detailed guide on how to do it:
-
Identify the Numerator and Denominator: The fraction \( \frac{25}{144} \) consists of a numerator (25) and a denominator (144).
-
Find the Square Root of the Numerator: Calculate \( \sqrt{25} \). Since 25 is a perfect square, \( \sqrt{25} = 5 \).
-
Find the Square Root of the Denominator: Calculate \( \sqrt{144} \). Since 144 is a perfect square, \( \sqrt{144} = 12 \).
-
Combine the Square Roots: According to the property of square roots, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). Therefore, \( \sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}} \).
-
Simplify the Fraction: Substitute the simplified square roots back into the fraction:
\[
\sqrt{\frac{25}{144}} = \frac{5}{12}
\]
Thus, the simplified form of \( \sqrt{\frac{25}{144}} \) is \( \frac{5}{12} \). This method can be applied to any fraction where both the numerator and the denominator are perfect squares.
Decimal Approximation of √(25/144)
While we can simplify \( \sqrt{\frac{25}{144}} \) to \( \frac{5}{12} \), finding the decimal approximation involves converting this fraction into a decimal. Here is a step-by-step guide:
-
Simplify the Square Root: We have already determined that \( \sqrt{\frac{25}{144}} = \frac{5}{12} \).
-
Convert the Fraction to Decimal: To find the decimal approximation, divide the numerator by the denominator:
\[
\frac{5}{12} = 0.416666...
\] -
Round the Decimal (if necessary): For practical purposes, you might round the decimal to a certain number of places. Commonly, two decimal places are sufficient:
\[
0.416666... \approx 0.42
\] -
Verify the Result: It's always good to double-check your calculations, especially when rounding:
- \( \frac{5}{12} = 0.416666... \)
- Rounded to two decimal places: \( 0.42 \)
Thus, the decimal approximation of \( \sqrt{\frac{25}{144}} \) is approximately \( 0.42 \). This method can be applied to find the decimal approximation of any simplified square root of a fraction.
Visual Representation of √(25/144)
The square root of the fraction 25/144 can be visually represented using the properties of square roots and fractions.
First, let's rewrite the expression:
\(\sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}} = \frac{5}{12}\)
To help visualize this, we can use a number line and a geometric representation:
- On a number line, mark the point 0 and the point 1.
- Divide the segment between 0 and 1 into 12 equal parts to represent twelfths.
- Mark the point corresponding to 5/12. This is the decimal approximation of the square root of 25/144, which is approximately 0.4167.
We can also use a square to visualize the square root. Consider a square with a side length of 1 unit:
- Divide this square into 144 smaller equal squares.
- Highlight 25 of these smaller squares to represent the numerator.
- The side length of the highlighted area will be the square root of 25/144, which corresponds to 5/12 of the unit square's side length.
Another way to represent it is using MathJax:
\[\sqrt{\frac{25}{144}} = \frac{5}{12}\]
This representation shows that taking the square root of a fraction is equivalent to taking the square roots of the numerator and the denominator separately and then forming a new fraction from these results.
The simplified form is an exact representation of the square root of 25/144 in its simplest fractional form, demonstrating the consistency and accuracy of mathematical operations involving square roots and fractions.
Applications of Square Roots in Real Life
Square roots are used in numerous real-life applications across various fields. Here are some key examples:
- Geometry and Architecture: Square roots are essential in calculating distances and dimensions. For example, the Pythagorean theorem, which involves square roots, is used to determine the lengths of sides in right triangles, aiding in the design and construction of buildings and other structures.
- Physics and Engineering: Square roots are used to calculate physical quantities such as velocity, acceleration, and energy. In engineering, they help determine the natural frequency of structures, which is crucial for ensuring stability and safety under various loads.
- Finance: In finance, square roots are used to compute stock market volatility, which helps investors assess risk. The standard deviation, a measure of risk, is the square root of the variance of a stock's returns.
- Statistics: Square roots play a vital role in statistical analysis, particularly in calculating the standard deviation, which measures the dispersion of data points from the mean.
- Computer Science: Square roots are utilized in algorithms for encryption, graphics, and data analysis. For example, they are used in calculating distances between points in computer graphics and in developing secure communication protocols in cryptography.
- Navigation: Pilots and navigators use square roots to calculate distances between points on a map, ensuring accurate and efficient route planning.
- Telecommunications: The inverse square law, which involves square roots, describes how signal strength decreases with distance, helping engineers design better communication systems.
These examples illustrate the wide-ranging importance of square roots in both everyday life and specialized fields.

Common Mistakes and How to Avoid Them
Finding the square root of a fraction like \( \sqrt{\frac{25}{144}} \) can lead to several common mistakes. Here are some of these mistakes and how to avoid them:
-
Forgetting to Simplify the Fraction:
It's essential to simplify the fraction before taking the square root. Simplifying \( \frac{25}{144} \) is not necessary here as both are already in simplest form, but always check this step.
-
Incorrectly Applying the Square Root:
The square root of a fraction should be taken by separately finding the square roots of the numerator and the denominator:
\( \sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}} \)
Which simplifies to:
\( \frac{5}{12} \)
-
Ignoring Both Positive and Negative Roots:
Remember that the square root of a number has both a positive and a negative solution. Thus, \( \sqrt{\frac{25}{144}} \) is both \( \frac{5}{12} \) and \( -\frac{5}{12} \).
-
Decimal Approximation Errors:
When approximating the square root as a decimal, ensure to use sufficient decimal places for accuracy. For example:
\( \sqrt{\frac{25}{144}} \approx \frac{5}{12} \approx 0.4167 \) (to 4 decimal places)
-
Not Checking the Result:
After computing the square root, always verify your result by squaring it to see if it returns to the original fraction:
\( \left(\frac{5}{12}\right)^2 = \frac{25}{144} \)
If it does, then the calculation is correct.
By being aware of these common mistakes and following these steps, you can accurately find the square root of fractions like \( \frac{25}{144} \).
Practice Problems and Solutions
To reinforce your understanding of finding the square root of a fraction, here are some practice problems along with detailed solutions:
Problem 1: Basic Square Root of a Fraction
Calculate the square root of \( \frac{25}{144} \).
- Identify the numerator and denominator:
- Numerator: 25
- Denominator: 144
- Take the square root of the numerator and the denominator separately:
- \( \sqrt{25} = 5 \)
- \( \sqrt{144} = 12 \)
- Combine the results to get:
\[
\sqrt{\frac{25}{144}} = \frac{\sqrt{25}}{\sqrt{144}} = \frac{5}{12}
\]
Problem 2: Square Root of a Simplified Fraction
Calculate the square root of \( \frac{9}{16} \).
- Identify the numerator and denominator:
- Numerator: 9
- Denominator: 16
- Take the square root of the numerator and the denominator separately:
- \( \sqrt{9} = 3 \)
- \( \sqrt{16} = 4 \)
- Combine the results to get:
\[
\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}
\]
Problem 3: Square Root of a More Complex Fraction
Calculate the square root of \( \frac{49}{121} \).
- Identify the numerator and denominator:
- Numerator: 49
- Denominator: 121
- Take the square root of the numerator and the denominator separately:
- \( \sqrt{49} = 7 \)
- \( \sqrt{121} = 11 \)
- Combine the results to get:
\[
\sqrt{\frac{49}{121}} = \frac{\sqrt{49}}{\sqrt{121}} = \frac{7}{11}
\]
Problem 4: Square Root of a Fraction with a Larger Denominator
Calculate the square root of \( \frac{81}{400} \).
- Identify the numerator and denominator:
- Numerator: 81
- Denominator: 400
- Take the square root of the numerator and the denominator separately:
- \( \sqrt{81} = 9 \)
- \( \sqrt{400} = 20 \)
- Combine the results to get:
\[
\sqrt{\frac{81}{400}} = \frac{\sqrt{81}}{\sqrt{400}} = \frac{9}{20}
\]
Solutions Recap
| Problem | Fraction | Square Root |
|---|---|---|
| 1 | \( \frac{25}{144} \) | \( \frac{5}{12} \) |
| 2 | \( \frac{9}{16} \) | \( \frac{3}{4} \) |
| 3 | \( \frac{49}{121} \) | \( \frac{7}{11} \) |
| 4 | \( \frac{81}{400} \) | \( \frac{9}{20} \) |
These practice problems will help solidify your understanding of how to find and simplify the square root of fractions. Keep practicing to master this concept!
Further Reading and Resources
For a deeper understanding of the concepts covered in this article, you may find the following resources helpful:
- - This resource provides comprehensive lessons and exercises on square roots, including detailed explanations and practice problems.
- - A useful guide to understanding radicals, including how to simplify and calculate square roots of fractions.
- - An accessible resource that explains the concept of square roots with interactive examples and visual aids.
- - Offers detailed explanations and practice exercises for simplifying square roots, including those of fractions.
- - Provides a step-by-step guide to finding the square roots of fractions, with helpful examples and tips.
Additionally, the following books and articles can further enhance your understanding:
- Understanding Algebra by James Brennan - A comprehensive book covering a wide range of algebraic concepts, including square roots and their applications.
- Elementary Algebra by Harold R. Jacobs - This book offers clear explanations and numerous practice problems related to square roots and fractions.
- - An article exploring different methods for teaching square roots, with a focus on visual learning techniques.
These resources will provide you with a wealth of information and practice opportunities to master the calculation and application of square roots, particularly for fractions like 25/144.
Xem video để học cách đơn giản hóa biểu thức với căn bậc hai “√(25) + √(144)” qua từng bước giải đại số. Phù hợp cho người học toán.
Đơn Giản Hóa Biểu Thức với Căn Bậc Hai “√(25) + √(144)” | Hướng Dẫn Từng Bước Giải Đại Số
READ MORE:
Xem video để tìm hiểu cách đơn giản hóa biểu thức (√(225/729)-√(25/144))+√(16/81). Phù hợp cho người học toán.
(√(225/729)-√(25/144))+√(16/81)