Topic what is the square root of 122: What is the square root of 122? Dive into this article to find out! We explore its mathematical properties, methods of calculation, and practical applications. Whether you're a student or just curious, this comprehensive guide will enhance your understanding of this fascinating topic.
Table of Content
- Square Root of 122
- Introduction to the Square Root of 122
- Definition and Basic Properties
- Methods to Calculate the Square Root
- Prime Factorization
- Long Division Method
- Decimal Form and Exact Form
- Applications in Geometry
- Examples and Real-World Problems
- Use in Technology
- FAQ on Square Root of 122
- Comparative Table of Square Roots Around 122
- Conclusion
- YOUTUBE: Khám phá căn bậc hai của 122 qua video này để hiểu rõ hơn về khái niệm và ứng dụng thực tế của nó. Thích hợp cho học sinh và những người đam mê toán học.
Square Root of 122
The square root of 122 is approximately 11.045. This value can be expressed in both decimal and radical forms, and it is an important concept in various mathematical contexts.
Definition and Calculation
The square root of a number is defined as a value that, when multiplied by itself, gives the original number. For 122, the square root is:
$$ \sqrt{122} \approx 11.045 $$
Methods to Calculate
- Prime Factorization: This method is typically used for perfect squares but can show that 122 is not a perfect square, hence leading to an irrational number.
- Long Division: This method is more suitable for numbers that result in a decimal value. Using long division, the square root of 122 is calculated to be approximately 11.045.
Examples
- Solve the equation \( x^2 - 122 = 0 \)
Solution: \( x = \pm \sqrt{122} = \pm 11.045 \)
- If the area of an equilateral triangle is \( 122\sqrt{3} \, \text{in}^2 \), find the side length.
Solution: \( a = \sqrt{488} = 2\sqrt{122} \approx 22.091 \, \text{in} \)
- If the surface area of a sphere is \( 488\pi \, \text{in}^2 \), find the radius.
Solution: \( r = \sqrt{122} \approx 11.045 \, \text{in} \)
Properties
The square root of 122 is an irrational number because it cannot be expressed as a simple fraction and its decimal form is non-terminating and non-repeating.
Table of Roots for 122
| Index | Root Symbol | Value |
| 2 | \(\sqrt[2]{122}\) | ±11.045 |
| 3 | \(\sqrt[3]{122}\) | 4.960 |
| 4 | \(\sqrt[4]{122}\) | ±3.323 |
| 5 | \(\sqrt[5]{122}\) | 2.614 |
| 6 | \(\sqrt[6]{122}\) | ±2.227 |
Knowing the square root of 122 and understanding its properties can be useful in various mathematical applications and problem-solving scenarios.
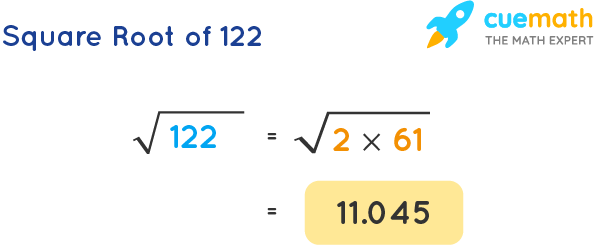
READ MORE:
Introduction to the Square Root of 122
The square root of 122, denoted as √122, is a number that, when multiplied by itself, equals 122. Mathematically, it can be expressed as follows:
\[
\sqrt{122} \approx 11.045361017187
\]
This value is an irrational number, meaning it cannot be precisely expressed as a fraction and its decimal representation is non-repeating and non-terminating. The principal (positive) square root of 122 is approximately 11.045, while the negative square root is approximately -11.045.
Below are the steps and methods to understand and calculate the square root of 122:
- Basic Calculation: Using a calculator, you can find the square root by entering 122 and pressing the square root button (√). This gives a value of approximately 11.045.
- Manual Calculation: Historically, long division methods were used to manually compute square roots, which involves iterative approximation techniques.
- Excel and Google Sheets: You can use the SQRT function in these spreadsheet programs. For instance, =SQRT(122) yields 11.045361017187.
The square root of 122 is not a perfect square, meaning it does not result in a whole number. However, it can be expressed in radical form and approximated to various decimal places as needed:
- To the nearest integer: √122 ≈ 11
- To one decimal place: √122 ≈ 11.0
- To two decimal places: √122 ≈ 11.05
Furthermore, the square root can also be represented with an exponent: \[ \sqrt{122} = 122^{1/2} \].
For practical applications, such as engineering and science, these approximations are often sufficient to solve problems requiring the square root of 122.
Definition and Basic Properties
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 122 is represented as √122, which is approximately equal to 11.045. Here are some important points about the square root of 122:
- The square root of 122 is an irrational number because it cannot be expressed as a simple fraction.
- The positive square root of 122 is called the principal square root and is approximately 11.045.
- When calculating the square root of 122, it can be represented in both radical form (√122) and decimal form (11.045).
- Square roots can be calculated using various methods such as factorization, estimation, or using a calculator.
To understand the square root of 122 more clearly, consider the following examples:
- If x2 = 122, then x = ±√122. This means x can be either +11.045 or -11.045.
- If the area of a square is 122 square units, then the length of each side of the square is √122, which is approximately 11.045 units.
Here is a table summarizing the key properties:
| Number | Square Root | Property |
| 122 | √122 ≈ 11.045 | Irrational |
Methods to Calculate the Square Root
There are several methods to calculate the square root of a number, such as the square root of 122. Here, we will discuss three common methods: prime factorization, the long division method, and the Babylonian (or Heron’s) method.
Prime Factorization
Prime factorization involves breaking down the number into its prime factors and simplifying the radical. However, since 122 is a product of two primes, 2 and 61, it cannot be simplified further:
\[
\sqrt{122} = \sqrt{2 \times 61}
\]
Thus, the square root of 122 is approximately 11.045361017187 in its decimal form.
Long Division Method
The long division method is a manual technique to find the square root of a number to a desired degree of accuracy. Here are the steps to find the square root of 122 using this method:
- Pair the digits of the number from right to left.
- Find the largest number whose square is less than or equal to the first pair or single digit.
- Subtract the square of the number found in step 2 from the first pair or single digit, and bring down the next pair of digits.
- Double the number found in step 2 and write it down with a blank space on its right.
- Find a digit to fill the blank space such that when the new number is multiplied by the digit, the product is less than or equal to the current dividend.
- Repeat steps 3-5 until you reach the desired precision.
Babylonian (or Heron's) Method
The Babylonian method is an iterative algorithm to approximate the square root of a number. Here are the steps:
- Make an initial guess for the square root (e.g., half of 122).
- Calculate the error by dividing 122 by the guess and finding the arithmetic mean of the guess and the result.
- Use the mean as the new guess and repeat the process until the error is less than a predefined tolerance.
For 122, the steps would look like this:
- Initial guess: 61 (122/2).
- Calculate: \(\frac{61 + \frac{122}{61}}{2} = 31.5\)
- Calculate: \(\frac{31.5 + \frac{122}{31.5}}{2} = 17.6865\)
- Calculate: \(\frac{17.6865 + \frac{122}{17.6865}}{2} = 12.2922\)
- Continue iterations until the result stabilizes around 11.0454.
Using these methods, one can calculate the square root of 122 with varying degrees of accuracy and efficiency.
Prime Factorization
The prime factorization of a number involves breaking it down into its smallest prime factors. Here is the detailed process for finding the prime factorization of 122:
- Start by dividing the number by the smallest prime number, which is 2.
- 122 ÷ 2 = 61
- Check if the resulting quotient is a prime number.
- 61 is a prime number.
- Write the prime factorization of 122.
- Prime factorization of 122 = 2 × 61
Thus, the prime factors of 122 are 2 and 61. This method shows that 122 can be expressed as the product of these two prime numbers.
| Number | Prime Factors |
| 122 | 2, 61 |
By understanding the prime factorization of 122, we can simplify its square root. Since neither of the prime factors repeats, the square root of 122 cannot be simplified further. In mathematical notation:
\[
\sqrt{122} = \sqrt{2 \times 61}
\]
This represents the simplest radical form of the square root of 122.

Long Division Method
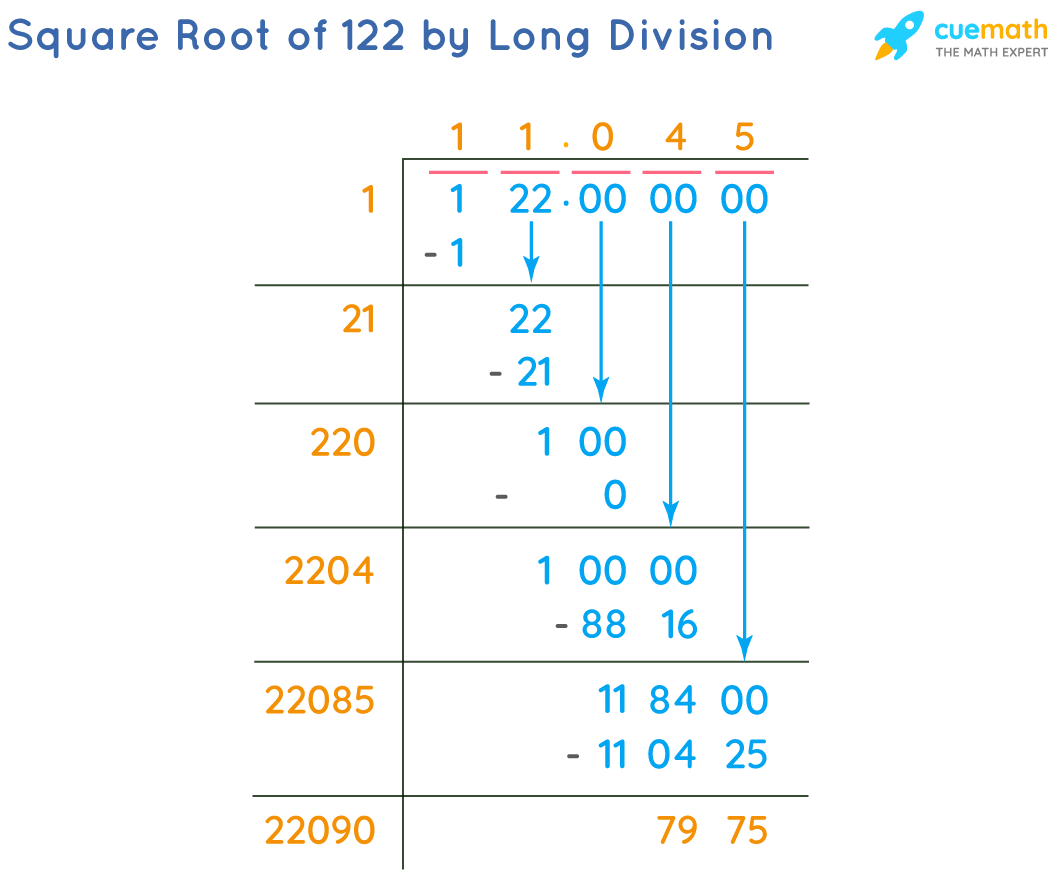
The long division method is a systematic way to find the square root of a number. Below are the detailed steps to find the square root of 122 using this method:
-
Start by pairing the digits of the number from the decimal point. For 122, we pair it as (1)(22).
-
Find the largest number whose square is less than or equal to the first pair (1). In this case, the number is 1 because \(1^2 = 1\).
-
Subtract the square of this number from the first pair and bring down the next pair of digits to the right. This gives us (22).
-
Double the quotient obtained so far (1), which gives 2, and place it as the new divisor with a blank digit on its right (20_).
-
Determine the largest digit (X) that fits into the blank so that \(20X \times X\) is less than or equal to 22. Here, \(20 \times 1 = 20\) is the best fit.
-
Place this digit in the quotient and the divisor. Subtract \(20\) from \(22\) to get a remainder of \(2\).
-
Bring down two zeros (since 122 is an integer), making the new number 200. Repeat the process to find more decimal places if needed.
Following these steps, the square root of 122 can be approximated to several decimal places, ensuring a precise result.
Decimal Form and Exact Form
The square root of 122 can be expressed in both decimal and exact forms. Understanding these forms helps in various mathematical calculations and practical applications.
Exact Form: The exact form of the square root of 122 is represented as √122. Since 122 cannot be simplified further into a product of smaller square roots, it remains in this radical form.
Decimal Form: The decimal form of the square root of 122 is approximately 11.045361017187. This form is obtained through numerical methods such as long division or using a calculator.
- The square root of 122 in decimal form is an irrational number, meaning it has non-repeating, non-terminating decimal digits.
- The value in decimal form is crucial for practical calculations where an approximate value is sufficient.
Knowing both forms is essential: the exact form is used for theoretical work, while the decimal form is often used in practical applications and problem-solving.
Applications in Geometry
The square root of 122, approximately 11.045, finds several applications in geometry. These applications often involve calculations related to distances, areas, and other geometric properties.
1. Calculating the Diagonal of a Rectangle
In a rectangle with sides of 11 units and another side of approximately 11.045 units, the diagonal can be calculated using the Pythagorean theorem:
\[ \text{Diagonal} = \sqrt{(11^2 + 11.045^2)} \]
This results in a diagonal length of:
\[ \sqrt{(121 + 122)} = \sqrt{243} \approx 15.59 \]
2. Finding the Side Length of an Equilateral Triangle
If the area of an equilateral triangle is given as \(122 \sqrt{3}\) square units, we can find the side length as follows:
Using the formula for the area of an equilateral triangle:
\[ \text{Area} = \frac{\sqrt{3}}{4} a^2 \]
Setting the area equal to \(122 \sqrt{3}\):
\[ 122 \sqrt{3} = \frac{\sqrt{3}}{4} a^2 \]
Solving for \(a\):
\[ a^2 = 488 \]
\[ a = \sqrt{488} = \sqrt{4 \times 122} = 2 \sqrt{122} \]
Since \(\sqrt{122} \approx 11.045\), the side length \(a\) is:
\[ a \approx 22.09 \text{ units} \]
3. Determining the Radius of a Sphere
If a sphere has a surface area of \(488 \pi\) square units, the radius can be determined as follows:
Using the formula for the surface area of a sphere:
\[ \text{Surface Area} = 4 \pi r^2 \]
Setting the surface area equal to \(488 \pi\):
\[ 4 \pi r^2 = 488 \pi \]
Solving for \(r^2\):
\[ r^2 = 122 \]
\[ r = \sqrt{122} \approx 11.045 \text{ units} \]
4. Distance Between Two Points
The square root of 122 can also be used to find the distance between two points in a plane. For example, the distance \(D\) between points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
If the calculated distance is approximately \(\sqrt{122}\), it represents a distance of about 11.045 units.
5. Application in Special Right Triangles
In special right triangles like 45-45-90 and 30-60-90 triangles, the side lengths involve square roots. For instance, in a 30-60-90 triangle, the ratio of the sides is \(1 : \sqrt{3} : 2\). If one of the sides involves the square root of 122, the calculations can leverage this value directly.
These examples illustrate the practical uses of the square root of 122 in various geometric contexts, highlighting its importance in solving real-world geometric problems.
Examples and Real-World Problems
Understanding the square root of 122 can be applied to various real-world scenarios. Here are some practical examples and problems involving the square root of 122:
Example 1: Estimating Distance
Imagine you are trying to estimate the diagonal distance across a rectangular field where the length is approximately 100 meters and the width is approximately 22 meters. Using the Pythagorean theorem, the diagonal distance (d) can be calculated as:
\[
d = \sqrt{100^2 + 22^2} = \sqrt{10000 + 484} = \sqrt{10484} \approx 102.4 \text{ meters}
\]
This is close to the square root of 122 multiplied by 10, highlighting its use in approximating distances in geometry.
Example 2: Architecture and Design
In architectural design, precise measurements are crucial. Suppose you are designing a square window with an area close to 122 square feet. The side length (s) of the window can be determined by finding the square root:
\[
s = \sqrt{122} \approx 11.05 \text{ feet}
\]
This allows architects to create a square window with each side approximately 11 feet.
Example 3: Engineering Calculations
Engineers often need to solve for values that involve square roots. For example, if a certain material has a stress limit that is proportional to the square root of 122, and they need to determine the maximum allowable stress, they would use:
\[
\text{Maximum Stress} = k \cdot \sqrt{122}
\]
where \( k \) is a constant based on material properties.
Word Problems
- Problem 1: A square garden has an area of 122 square feet. What is the length of one side of the garden?
Solution: The side length \( s \) is:
\[
s = \sqrt{122} \approx 11.05 \text{ feet}
\] - Problem 2: A rectangular park is 122 meters long. If the width is 1/5th of the length, what is the approximate diagonal distance across the park?
Solution:
Let the width be \( w \):
\[
w = \frac{122}{5} = 24.4 \text{ meters}
\]Using the Pythagorean theorem:
\[
d = \sqrt{122^2 + 24.4^2} \approx \sqrt{14884.16} \approx 122 \text{ meters}
\] - Problem 3: A square tile has an area of 122 square inches. What is the length of one side of the tile to the nearest hundredth?
Solution:
The side length \( s \) is:
\[
s = \sqrt{122} \approx 11.05 \text{ inches}
\]
These examples illustrate how the square root of 122 can be used in practical calculations, highlighting its relevance in different fields such as geometry, architecture, and engineering.
Use in Technology
The square root of 122, approximately 11.045, finds applications in various technological fields. Here are some notable examples:
- Engineering:
In engineering, precise measurements and calculations are essential. The square root of 122 can be used to determine dimensions in construction and design projects. For instance, it can help in calculating the length of a diagonal in a rectangular section where the sum of the squares of the sides is 122.
- Computer Graphics:
In computer graphics, the square root function is often used to normalize vectors, calculate distances, and in algorithms for rendering and image processing. For example, finding the Euclidean distance between two points in a 3D space might involve computing the square root of the sum of squared differences of their coordinates, where such calculations can involve values like 122.
- Signal Processing:
Signal processing algorithms frequently use square root operations. The square root of 122 can be part of calculations in digital filters or when analyzing signal power, as it often involves the root-mean-square (RMS) value of signals.
- Robotics:
In robotics, determining the exact positions, distances, and movements often requires precise calculations. For example, calculating the hypotenuse of a right-angled triangle, where the sum of the squares of the legs is 122, involves the square root of 122, which helps in path planning and navigation.
- Machine Learning:
In machine learning, distance metrics like Euclidean distance are used in clustering algorithms such as k-means. Calculating these distances may involve square roots of values around 122, helping to determine the similarity between data points.
- Physics Simulations:
Simulations in physics often require precise mathematical computations, including square roots. For instance, calculating the resultant vector magnitude when the squared components add up to 122 uses the square root of 122.
FAQ on Square Root of 122
-
What is the square root of 122?
The square root of 122 is approximately \( \sqrt{122} \approx 11.0453610172 \).
-
Is the square root of 122 a rational number?
No, the square root of 122 is an irrational number because it cannot be expressed as a simple fraction and its decimal form is non-terminating and non-repeating.
-
How can we express the square root of 122 in radical form?
In radical form, it is expressed as \( \sqrt{122} \).
-
What is the principal square root of 122?
The principal square root of 122 is the positive root, which is approximately 11.045.
-
How can the square root of 122 be used in mathematical problems?
It can be used in various calculations, such as determining the length of the side of a square with an area of 122 square units, or in solving quadratic equations where 122 is involved.
-
What methods can be used to calculate the square root of 122?
The square root of 122 can be calculated using methods like the long division method or using a calculator.
-
What are some approximate fractional representations of the square root of 122?
One rational approximation of \( \sqrt{122} \) is \( \frac{5357}{485} \), which is about 11.0453608.
-
What is the significance of knowing the square root of 122 in practical applications?
Knowing the square root of 122 is useful in fields such as engineering, physics, and computer science where precise calculations are needed.
-
Can the square root of 122 be simplified further?
No, \( \sqrt{122} \) cannot be simplified further because 122 does not have any repeated prime factors.
Comparative Table of Square Roots Around 122
The square root of 122 is approximately 11.045. Understanding how this value compares to the square roots of nearby numbers can be helpful for various mathematical and practical applications. Below is a comparative table showing the square roots of numbers around 122:
| Number | Square Root |
|---|---|
| 117 | 10.817 |
| 118 | 10.863 |
| 119 | 10.909 |
| 120 | 10.954 |
| 121 | 11.000 |
| 122 | 11.045 |
| 123 | 11.091 |
| 124 | 11.136 |
| 125 | 11.180 |
| 126 | 11.225 |
| 127 | 11.269 |
This table provides a clear comparison of the square roots of numbers immediately surrounding 122. These values are useful in estimating and understanding the relationship between the square roots of close numerical values.
Conclusion
The square root of 122 is approximately 11.045. Understanding this value involves recognizing its implications across various mathematical and practical applications. While 122 is not a perfect square, its square root is a non-repeating, non-terminating decimal, classifying it as an irrational number.
Throughout this guide, we have explored several methods to calculate the square root, including prime factorization and the long division method, highlighting their practical applications in different scenarios. We have also examined the geometric and technological applications of the square root of 122, showcasing its relevance in fields such as construction, engineering, and computer science.
In geometry, the square root of 122 can help determine the lengths of sides in right triangles and other geometric shapes. In technology, it plays a role in algorithms, computer graphics, and optimization problems, demonstrating its significance beyond theoretical mathematics.
By delving into real-world problems and examples, we've seen how this mathematical concept aids in solving practical issues, from architecture to digital design. The comparative analysis with other square roots provides a broader perspective on where 122 stands among its numerical neighbors.
In conclusion, the square root of 122 is a fascinating number that exemplifies the intersection of pure mathematics and practical utility. Its study not only enriches our understanding of numerical relationships but also equips us with tools to tackle diverse problems in various fields.
Khám phá căn bậc hai của 122 qua video này để hiểu rõ hơn về khái niệm và ứng dụng thực tế của nó. Thích hợp cho học sinh và những người đam mê toán học.
Căn bậc hai của 122
READ MORE:
Khám phá căn bậc hai của 122 qua video này để hiểu rõ hơn về khái niệm và ứng dụng thực tế của nó. Phù hợp cho học sinh và những người yêu thích toán học.
Căn Bậc Hai Của 122













