Topic square root of negative 1: The square root of negative 1, commonly represented as the imaginary unit "i", is a fundamental concept in mathematics that extends the real number system to the complex number plane. This introduction to imaginary numbers allows for the solution of equations that have no real solutions and plays a critical role in various fields such as engineering, physics, and signal processing.
Table of Content
- Understanding the Square Root of Negative One
- Introduction
- Definition of Imaginary Numbers
- Square Root of Negative Numbers
- Examples and Calculations
- Applications of Imaginary Numbers
- History and Development
- Complex Numbers and Their Uses
- YOUTUBE: Video về căn bậc hai của số âm giải thích khái niệm số ảo một cách dễ hiểu và hấp dẫn.
Understanding the Square Root of Negative One
In mathematics, the square root of a negative number is not a real number. Instead, it is defined as an imaginary number. The principal square root of -1 is denoted by the imaginary unit i, which is defined as follows:
\[\sqrt{-1} = i\]
This means that:
\[i^2 = -1\]
Properties of Imaginary Numbers
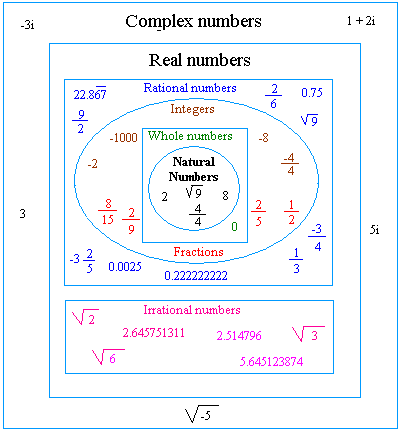
- Imaginary numbers are used in conjunction with real numbers to form complex numbers.
- The general form of a complex number is \(a + bi\), where a and b are real numbers.
Examples
Here are some examples to illustrate how to compute the square root of negative numbers:
| Expression | Calculation | Result |
|---|---|---|
| \(\sqrt{-4}\) | \(\sqrt{4 \times -1} = \sqrt{4} \times \sqrt{-1}\) | 2i |
| \(\sqrt{-9}\) | \(\sqrt{9 \times -1} = \sqrt{9} \times \sqrt{-1}\) | 3i |
| \(\sqrt{-25}\) | \(\sqrt{25 \times -1} = \sqrt{25} \times \sqrt{-1}\) | 5i |
Applications
Imaginary and complex numbers have various applications in different fields:
- Electrical Engineering: Complex numbers are used to analyze AC circuits.
- Signal Processing: Fourier transforms, which are essential for analyzing sound and image signals, use complex numbers.
- Quantum Mechanics: The wave functions used in quantum mechanics are often expressed in terms of complex numbers.
- Control Systems: Complex numbers help in the design and analysis of control systems.
Complex Plane
The complex plane, also known as the Argand plane, is used to represent complex numbers graphically. In this plane:
- The horizontal axis represents the real part of the number.
- The vertical axis represents the imaginary part of the number.
Summary
The square root of negative one is a fundamental concept in mathematics that leads to the introduction of imaginary numbers. These numbers are crucial for extending real numbers to complex numbers, allowing for a broader range of mathematical operations and applications.

READ MORE:
Introduction
The square root of negative one, represented as
Definition of Imaginary Numbers
Imaginary numbers are a fundamental concept in mathematics, essential for extending the real number system. The unit imaginary number is denoted by \( i \), which is defined as the square root of -1, expressed as \( \sqrt{-1} = i \). This definition allows us to handle the square roots of negative numbers, which are not possible within the real number system.
The key properties and uses of imaginary numbers can be summarized as follows:
- Imaginary Unit: The imaginary unit \( i \) satisfies \( i^2 = -1 \). This property is foundational for all computations involving imaginary numbers.
- Complex Numbers: Imaginary numbers combine with real numbers to form complex numbers, expressed in the form \( a + bi \), where \( a \) and \( b \) are real numbers.
- Operations: Basic arithmetic operations (addition, subtraction, multiplication, division) can be performed with imaginary and complex numbers using their properties and the definition of \( i \).
- Applications: Imaginary numbers are widely used in various fields, including engineering, physics, and signal processing. They are crucial in solving equations that have no real solutions and in analyzing oscillatory phenomena.
To understand imaginary numbers better, let's look at an example:
Example: What is the square root of -9?
The solution can be approached step by step:
- Express -9 as a product: \( -9 = 9 \times (-1) \).
- Apply the property of square roots: \( \sqrt{-9} = \sqrt{9 \times (-1)} \).
- Separate the square roots: \( \sqrt{9} \times \sqrt{-1} = 3 \times i \).
- Thus, \( \sqrt{-9} = 3i \).
In summary, imaginary numbers, through the introduction of the imaginary unit \( i \), enable the extension of the real number system and open up a broader range of mathematical possibilities.
Square Root of Negative Numbers
Calculating the square root of negative numbers introduces the concept of imaginary numbers, denoted by the symbol \( i \), where \( i \) is defined as the square root of -1. This concept allows us to extend our number system from real numbers to complex numbers, providing solutions to equations that do not have real solutions.
Here are some key points about the square root of negative numbers:
- Definition: For any positive real number \( p \), the square root of \( -p \) is defined as \( i\sqrt{p} \). This is because \( i^2 = -1 \), and thus \( (i\sqrt{p})^2 = i^2 \cdot p = -p \).
- Examples:
- \(\sqrt{-4} = i\sqrt{4} = 2i\)
- \(\sqrt{-9} = i\sqrt{9} = 3i\)
- Properties:
- Imaginary numbers follow the same arithmetic rules as real numbers, but with the additional property that \( i^2 = -1 \).
- When multiplying square roots of negative numbers, the property \( \sqrt{a} \cdot \sqrt{b} = \sqrt{ab} \) does not hold. For example, \( \sqrt{-1} \cdot \sqrt{-1} \neq \sqrt{1} \), since \( i \cdot i = i^2 = -1 \).
- Complex Numbers: Imaginary numbers are used to form complex numbers, which are numbers of the form \( a + bi \), where \( a \) and \( b \) are real numbers. This system extends the real number line into a complex plane.
In conclusion, the introduction of imaginary numbers allows us to solve equations and perform calculations that are not possible within the realm of real numbers alone, expanding our understanding and capabilities in mathematics.
Examples and Calculations
Understanding how to work with the square root of negative numbers is fundamental in complex number theory. Here are some detailed examples and calculations to illustrate this concept.
- Example 1:
- Find the square root of -16.
- Solution: The square root of -16 is calculated as follows:
Thus, \(\sqrt{-16} = 4i\).\(\sqrt{-16}\) = \(\sqrt{(-1) \cdot 16}\) = \(\sqrt{-1} \cdot \sqrt{16}\) = \(i \cdot 4\) = \(4i\) - Example 2:
- Find the square root of -9.
- Solution: The square root of -9 is calculated as follows:
Thus, \(\sqrt{-9} = 3i\).\(\sqrt{-9}\) = \(\sqrt{(-1) \cdot 9}\) = \(\sqrt{-1} \cdot \sqrt{9}\) = \(i \cdot 3\) = \(3i\) - Example 3:
- Find the square root of -25.
- Solution: The square root of -25 is calculated as follows:
Thus, \(\sqrt{-25} = 5i\).\(\sqrt{-25}\) = \(\sqrt{(-1) \cdot 25}\) = \(\sqrt{-1} \cdot \sqrt{25}\) = \(i \cdot 5\) = \(5i\)
These examples show the step-by-step process of finding the square roots of negative numbers using imaginary numbers.

Applications of Imaginary Numbers
Imaginary numbers, represented as multiples of the imaginary unit \(i\) where \(i\) is the square root of \(-1\), play a crucial role in various fields. Here are some of the key applications of imaginary numbers:
-
Electrical Engineering:
In electrical engineering, imaginary numbers are used to analyze and design alternating current (AC) circuits. The impedance of a circuit, which combines resistance and reactance, is expressed as a complex number \(Z = R + jX\), where \(R\) is resistance, \(X\) is reactance, and \(j\) is the imaginary unit (used instead of \(i\) to avoid confusion with current).
-
Control Systems:
Control engineers use imaginary numbers for stability analysis in control systems. The stability of a system can be determined by examining the poles of its transfer function in the complex plane.
-
Quantum Mechanics:
Imaginary numbers are essential in quantum mechanics, where they appear in the Schrödinger equation to describe the behavior of quantum systems. The wave function, which encodes the probabilities of a particle's position and momentum, often involves complex numbers.
-
Signal Processing:
In signal processing, complex numbers are used to represent sinusoidal signals. The Fourier transform, a mathematical technique to transform a signal into its frequency components, extensively uses complex numbers to simplify calculations and interpretations.
-
Fractals:
The Mandelbrot set and other fractals are generated using complex numbers. These fascinating mathematical structures are created by iterating complex functions and analyzing their behavior.
-
Fluid Dynamics:
In fluid dynamics, complex numbers help in solving potential flow problems. The velocity potential and stream function can be combined into a complex potential function, simplifying the analysis of fluid flows.
Imaginary numbers, once considered purely theoretical, now provide indispensable tools across science and engineering, facilitating the understanding and solving of complex real-world problems.
History and Development
The concept of the square root of negative one, denoted as \(i\), has a rich history dating back to ancient times. Initially, negative numbers were considered nonsensical, and their square roots were even more perplexing. However, mathematical advancements over centuries led to the formalization and acceptance of imaginary numbers.
Here is a timeline outlining the key developments in the history of imaginary numbers:
- Ancient Greece: Greek mathematicians, such as Pythagoras and Euclid, focused on geometric interpretations of numbers and avoided the concept of negative numbers.
- 16th Century: Italian mathematician Gerolamo Cardano is one of the first to consider the square roots of negative numbers in his work "Ars Magna" (1545). Although he didn't fully understand them, he recognized their necessity in solving cubic equations.
- 17th Century: Rafael Bombelli made significant strides by systematically working with complex numbers and providing rules for their arithmetic operations. He introduced the notation \(i\) for the square root of -1.
- 18th Century: Leonhard Euler and Carl Friedrich Gauss contributed greatly to the field. Euler popularized the notation \(i\) and explored its properties extensively. Gauss provided a rigorous foundation for complex numbers, demonstrating their applications in number theory and geometry.
- 19th Century: Augustin-Louis Cauchy and William Rowan Hamilton further developed the theory. Hamilton introduced the concept of quaternions, extending complex numbers to four dimensions. Cauchy's work on complex analysis laid the groundwork for modern mathematical analysis.
- 20th Century and Beyond: The advent of electrical engineering and quantum mechanics saw imaginary numbers become indispensable. They are now fundamental in fields such as signal processing, control theory, and fluid dynamics.
The development of imaginary numbers highlights the evolution of mathematical thought and its ability to embrace abstract concepts. Today, imaginary numbers are a crucial component of complex numbers, represented as \(a + bi\), where \(a\) and \(b\) are real numbers.
Complex Numbers and Their Uses
Complex numbers, represented in the form \(a + bi\), where \(a\) and \(b\) are real numbers and \(i\) is the imaginary unit with the property \(i^2 = -1\), play a crucial role in various fields of science and engineering.
Here are some key uses of complex numbers:
- Electrical Engineering:
- AC Circuit Analysis: Complex numbers are essential in analyzing alternating current (AC) circuits. They help in representing impedance, voltage, and current, allowing for easier calculations of phase differences and power consumption.
- Signal Processing: Complex numbers facilitate the analysis and manipulation of signals, particularly in Fourier transforms, which decompose signals into their frequency components.
- Quantum Mechanics:
Complex numbers are fundamental in quantum mechanics, where they are used to describe wave functions. The Schrödinger equation, which predicts how quantum systems evolve over time, relies on complex-valued functions.
- Control Theory:
In control systems, complex numbers are used to analyze and design systems for stability and performance. The use of the Laplace transform, which converts differential equations into algebraic equations in the complex plane, is a key application.
- Fluid Dynamics:
Complex analysis is employed to solve problems in fluid dynamics, especially in potential flow theory. Complex potentials simplify the study of incompressible and irrotational flows.
- Vibration Analysis:
In mechanical engineering, complex numbers are used to analyze vibrations and oscillations in structures and machinery. They help in solving differential equations that describe the motion of these systems.
- Computer Graphics:
Complex numbers are used in computer graphics for rotations and transformations. The manipulation of points in the complex plane allows for efficient algorithms in rendering images and animations.
- Dynamic Systems:
Complex numbers are used in the study of dynamic systems, including weather prediction, population models, and financial markets. They help in understanding the behavior of these systems over time.
The utility of complex numbers extends far beyond these examples, demonstrating their versatility and importance in both theoretical and applied sciences.
Video về căn bậc hai của số âm giải thích khái niệm số ảo một cách dễ hiểu và hấp dẫn.
Căn Bậc Hai Của Số Âm
READ MORE:
Video hướng dẫn cách tìm căn bậc hai của số âm, giải thích rõ ràng và dễ hiểu về số ảo.
Cách Tìm Căn Bậc Hai Của Một Số Âm