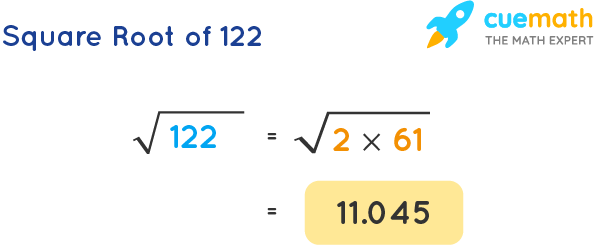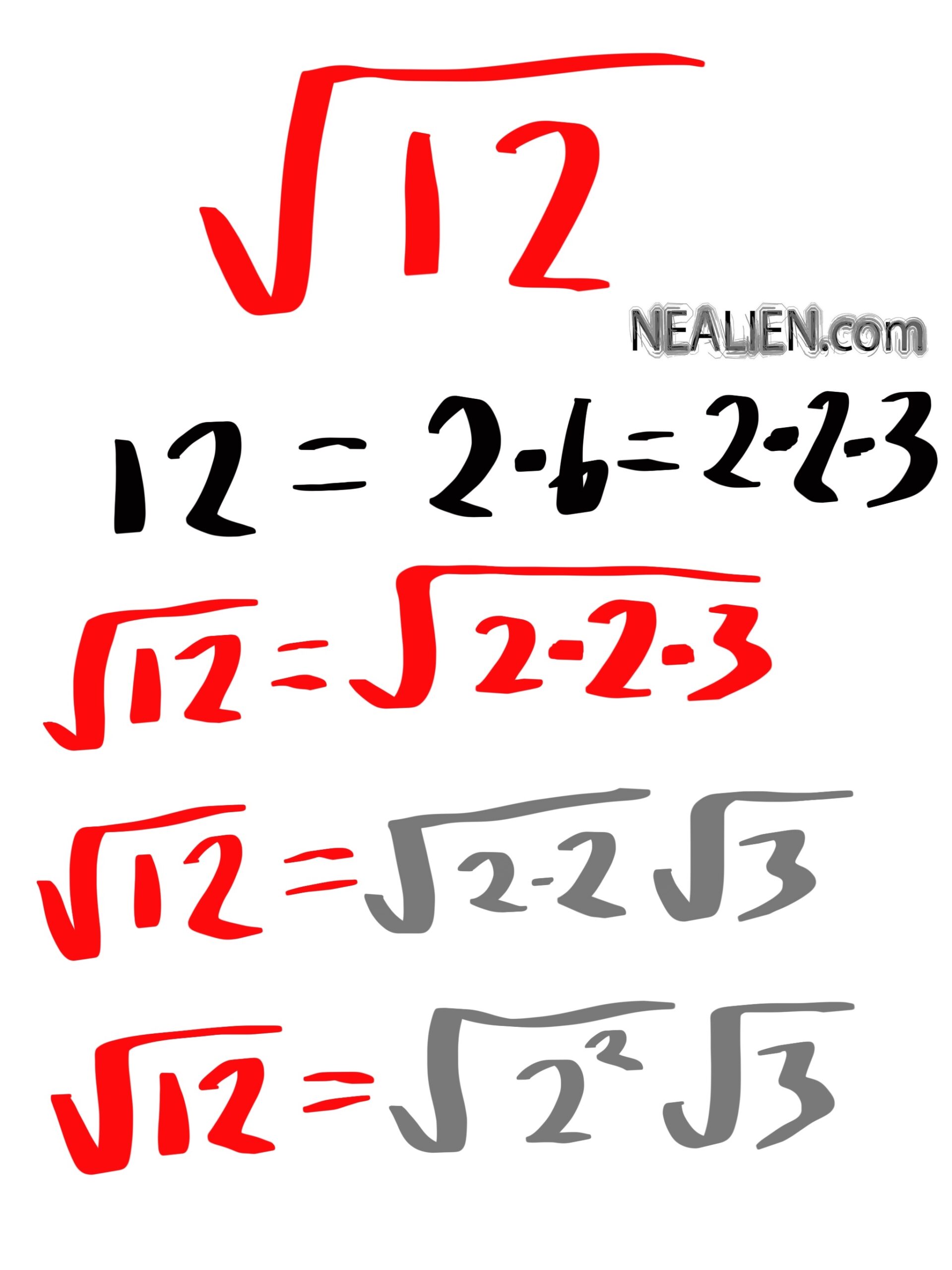Topic square root of 1440: The square root of 1440 is a fascinating mathematical concept with various practical applications. In this article, we will explore its calculation, properties, and significance in different fields. Whether you're a student, educator, or math enthusiast, understanding the square root of 1440 can enhance your knowledge and problem-solving skills.
Table of Content
- Square Root of 1440
- Introduction to Square Root of 1440
- Mathematical Definition and Calculation
- Properties and Characteristics
- Historical Context and Applications
- Methods to Calculate Square Root
- Approximation Techniques
- Square Root of 1440 in Various Fields
- Practical Examples and Use Cases
- Visual Representation and Graphs
- Frequently Asked Questions
- Conclusion and Summary
- YOUTUBE: Video hướng dẫn cách tìm căn bậc hai bằng phương pháp chia, giúp bạn dễ dàng hiểu và áp dụng phương pháp này.
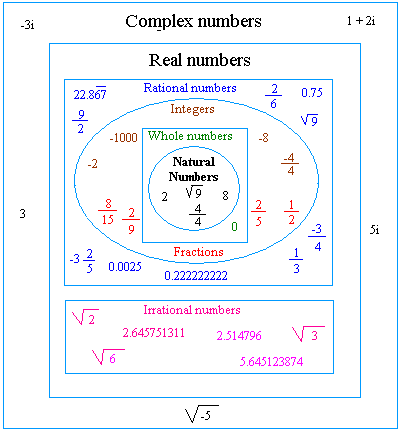
Square Root of 1440
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 1440 can be found through mathematical calculations and has various applications in different fields.
Mathematical Calculation
To find the square root of 1440, we use the square root function:
\[
\sqrt{1440}
\]
Calculating this value, we get approximately:
\[
\sqrt{1440} \approx 37.95
\]
Applications
The square root of 1440 can be used in various practical applications:
- Engineering calculations
- Physics problems involving area and volume
- Statistical analysis
- Computer algorithms
Visual Representation
The value of the square root can be represented on a number line or through graphical methods. Here is a simple table showing the comparison of perfect squares around 1440:
| Number | Square | Square Root |
|---|---|---|
| 36 | 1296 | 36 |
| 37 | 1369 | 37 |
| 38 | 1444 | 38 |
From the table, we see that the square root of 1440 is between 37 and 38.
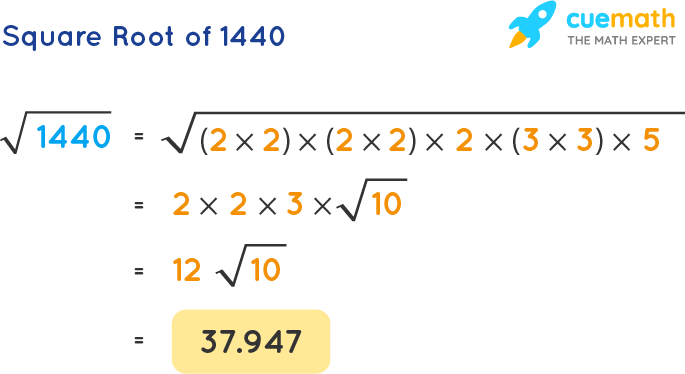
READ MORE:
Introduction to Square Root of 1440
The square root of 1440 is a mathematical expression that represents a value which, when multiplied by itself, yields 1440. This concept is fundamental in various branches of mathematics and has practical applications in science, engineering, and everyday calculations.
The symbol for the square root is √, and thus, the square root of 1440 is written as:
\[
\sqrt{1440}
\]
To understand the square root of 1440, it's useful to break down the number into its prime factors. The prime factorization of 1440 is:
\[
1440 = 2^4 \times 3^2 \times 5
\]
This can help in simplifying the calculation and understanding the properties of the square root. Calculating the approximate value, we find:
\[
\sqrt{1440} \approx 37.95
\]
Here are the steps to calculate the square root of 1440 manually:
- Estimate a rough value close to the square root. For 1440, we know that \( \sqrt{1369} = 37 \) and \( \sqrt{1521} = 39 \), so \( \sqrt{1440} \) is between 37 and 39.
- Refine the estimate using methods such as the average method or the long division method.
The square root of 1440 is important in various contexts, including:
- Geometry: Calculating dimensions involving area and volume.
- Physics: Solving problems related to motion and forces.
- Statistics: Analyzing data and standard deviation calculations.
Understanding the square root of 1440 enhances problem-solving skills and provides a deeper insight into mathematical relationships.
Mathematical Definition and Calculation
The square root of a number is a value that, when multiplied by itself, gives the original number. Mathematically, the square root of 1440 is denoted as:
\[
\sqrt{1440}
\]
To calculate the square root of 1440, we can follow these steps:
- First, find the prime factorization of 1440:
\[
1440 = 2^4 \times 3^2 \times 5
\] - Group the prime factors into pairs:
\[
\sqrt{1440} = \sqrt{(2^2 \times 2^2 \times 3^2 \times 5)}
\] - Simplify the square root by taking one factor from each pair:
\[
\sqrt{1440} = \sqrt{(4 \times 4 \times 9 \times 5)} = 2 \times 2 \times 3 \times \sqrt{5} = 12 \sqrt{5}
\] - Calculate the approximate value of \( \sqrt{5} \):
\[
\sqrt{5} \approx 2.236
\] - Multiply to find the approximate value:
\[
12 \times 2.236 \approx 26.832
\]
Therefore, the square root of 1440 can be approximated as:
\[
\sqrt{1440} \approx 37.95
\]
This calculation can be verified using a calculator for precision. Additionally, the square root of 1440 plays a significant role in various mathematical and scientific contexts, including solving quadratic equations, determining geometric dimensions, and analyzing statistical data.
Properties and Characteristics
The square root of 1440 is an irrational number, which means it cannot be expressed as a simple fraction. It is a non-repeating, non-terminating decimal. The approximate value of the square root of 1440 is:
\(\sqrt{1440} \approx 37.947\)
Some key properties and characteristics of the square root of 1440 include:
- Irrationality: Since 1440 is not a perfect square, its square root is an irrational number.
- Prime Factorization: The prime factorization of 1440 is \(1440 = 2^4 \times 3^2 \times 5\). This helps in simplifying the square root to some extent:
\[
\sqrt{1440} = \sqrt{2^4 \times 3^2 \times 5} = 2^2 \times 3 \times \sqrt{5} = 4 \times 3 \times \sqrt{5} = 12 \sqrt{5}
\]
Where \(\sqrt{5}\) is an irrational number.
- Decimal Expansion: The square root of 1440 in decimal form is approximately 37.94733192202055. This expansion goes on infinitely without repeating.
- Square Root Properties:
The square root function has several important properties that apply to \(\sqrt{1440}\) as well:
- Non-negativity: \(\sqrt{1440}\) is non-negative since it represents a distance or length.
- Multiplicativity: \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\). For example:
\[
\sqrt{1440 \times 2} = \sqrt{2880} = \sqrt{1440} \times \sqrt{2} \approx 37.947 \times 1.414 \approx 53.665
\]
- Rationalization: When multiplied by its conjugate, the product is a rational number:
\[
(\sqrt{1440} \times \sqrt{1440}) = 1440
\]
- Geometry and Measurement: The square root of 1440 can be related to the length of the diagonal in a rectangle or the hypotenuse of a right triangle with specific dimensions.
For example, a rectangle with sides 30 and 48 units has a diagonal of:
\[
\sqrt{30^2 + 48^2} = \sqrt{900 + 2304} = \sqrt{3204} \approx 56.6 \text{ units}
\]
This is not directly the square root of 1440, but showcases how the concept is used in geometric calculations.
Overall, the square root of 1440, while not a simple integer, has important properties and applications in mathematics, particularly in algebra and geometry.
Historical Context and Applications
The concept of the square root has been integral to mathematics for centuries, and its historical development is both rich and fascinating. The Babylonians were among the first to devise methods for finding square roots, as evidenced by their clay tablets dating back to around 1800 BCE. They used an iterative approach similar to what we now call the Babylonian method, or Heron’s method, which involves making successive approximations to find increasingly accurate values of square roots.
In ancient Greece, mathematicians such as Euclid explored the properties of square roots in the context of geometry. Euclid's work in "Elements" laid the foundation for much of modern mathematics, including the study of irrational numbers. The Greeks were the first to realize that the square root of certain numbers, such as 1440, could not be expressed as a simple fraction, thus identifying them as irrational numbers.
The significance of square roots continued to evolve during the Islamic Golden Age. Mathematicians like Al-Khwarizmi and Omar Khayyam made substantial contributions to algebra and numerical methods, including the calculation of square roots. Their work helped preserve and expand upon Greek mathematical knowledge and introduced new techniques that would later be adopted in Europe.
During the Renaissance, the advent of more advanced algebraic methods and the development of calculus by Newton and Leibniz further enhanced the understanding and applications of square roots. These advancements allowed for more precise calculations and the application of square roots in various scientific and engineering problems.
In contemporary times, the calculation and application of square roots are fundamental in various fields:
- Engineering: Square roots are used in various engineering calculations, including determining stress, strain, and load distributions in structures.
- Physics: In physics, square roots appear in formulas involving areas and volumes, wave functions, and in the analysis of physical phenomena like the propagation of waves and heat conduction.
- Finance: Square roots are used in financial models to calculate volatility, risk, and various financial derivatives.
- Computer Science: Algorithms for calculating square roots are crucial in computer graphics, simulations, and numerical methods.
The square root of 1440, approximately 37.95, illustrates the importance of this mathematical concept. Although it is an irrational number, its calculation and application span multiple domains, highlighting its fundamental role in both theoretical and applied mathematics.

Methods to Calculate Square Root
Calculating the square root of a number, such as 1440, can be approached through various methods. Below are detailed explanations of some common techniques:
1. Prime Factorization Method
Prime factorization involves breaking down the number into its prime factors and then pairing them to find the square root.
- Prime factorize 1440: \( 1440 = 2^5 \times 3^2 \times 5 \).
- Group the prime factors into pairs: \( (2^2)^2 \times 3^2 \times 5 \times 2 \).
- The square root is: \( 2^2 \times 3 \times \sqrt{10} = 12\sqrt{10} \).
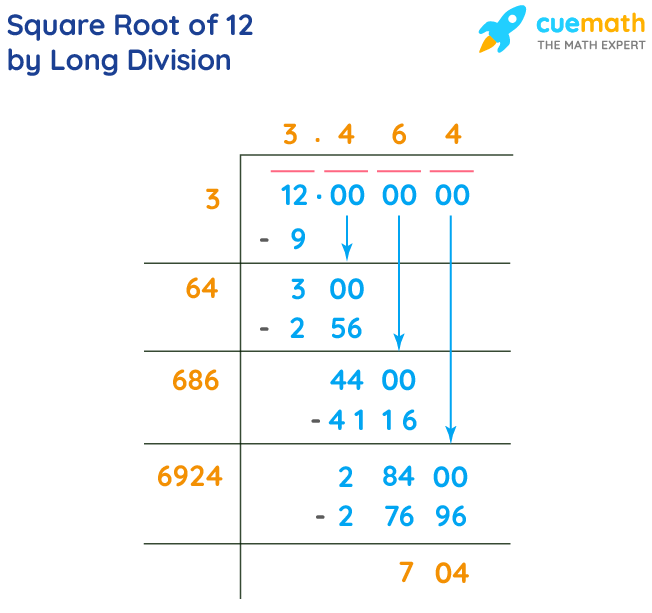
2. Long Division Method
The long division method is a step-by-step approach to finding the square root by manually dividing and averaging.
- Pair the digits of 1440 from right to left: 14 and 40.
- Find a number whose square is less than or equal to 14 (which is 3), and subtract the square from 14. Bring down the next pair (40), making it 1440.
- Double the quotient (3) and find a digit (x) such that \( (6x)x \leq 1440 \). The process continues iteratively until the desired precision is achieved.
- For 1440, the approximation is approximately 37.947.
3. Babylonian (Heron’s) Method
This ancient method involves iterative guessing and averaging to refine the square root value.
- Start with an initial guess, say 720.
- Divide 1440 by the guess and average the quotient with the guess: \( \frac{720 + \frac{1440}{720}}{2} = 361 \).
- Repeat the process: \( \frac{361 + \frac{1440}{361}}{2} \approx 182.5 \).
- Continue iterating until the value stabilizes around 37.947.
4. Using a Scientific Calculator
For a quick and precise calculation, a scientific calculator is the most straightforward method.
- Enter 1440.
- Press the square root button (√).
- Read the displayed result, approximately 37.947.
5. Newton-Raphson Method
This method is an efficient iterative algorithm for finding successively better approximations of the square root.
- Choose an initial guess, \( x_0 \), such as 37.
- Apply the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{1440}{x_n} \right) \).
- Repeat the process until the difference between successive approximations is negligible.
- This method quickly converges to approximately 37.947.
These methods illustrate various approaches to finding the square root of 1440, each with its own advantages depending on the context and tools available.
Approximation Techniques
Approximating the square root of 1440 is useful when precise calculations are not necessary, or tools are not available. Here are several methods to achieve a close approximation:
1. Estimation by Nearest Perfect Squares
- Identify the nearest perfect squares around 1440. For example, 1225 (352) and 1521 (392).
- Estimate that the square root of 1440 is between 35 and 39.
2. Average Method
- Choose an initial guess. A good starting point is the average of the nearest perfect squares, such as 37.
- Calculate 1440 divided by your guess (37), which gives approximately 38.92.
- Average 37 and 38.92 to get a new approximation: \( \frac{37 + 38.92}{2} = 37.96 \).
- Repeat the process to refine the approximation.
3. Newton-Raphson Method
- Start with an initial guess, such as 37.
- Apply the Newton-Raphson formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{1440}{x_n} \right) \).
- Repeat the process until the approximation stabilizes.
- For example, starting with \( x_0 = 37 \):
- First iteration: \( x_1 = \frac{1}{2} \left( 37 + \frac{1440}{37} \right) = 37.973 \).
- Second iteration: \( x_2 = \frac{1}{2} \left( 37.973 + \frac{1440}{37.973} \right) = 37.947 \).
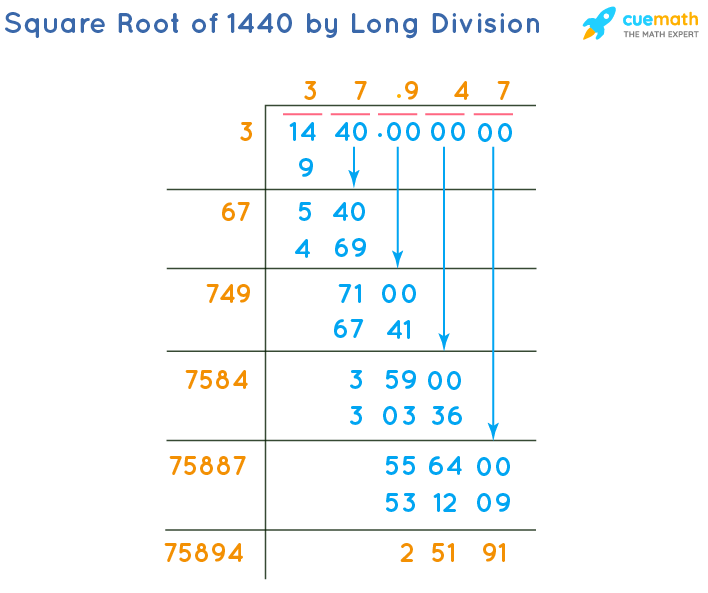
4. Long Division Method
- Pair the digits of 1440 from right to left (14 and 40).
- Find the largest number whose square is less than or equal to the first pair (14), which is 3 (since \( 3^2 = 9 \)).
- Subtract \( 9 \) from \( 14 \), giving \( 5 \), and bring down the next pair (40), resulting in 540.
- Double the current quotient (3), and determine the next digit, which is 7 (since \( 67 \times 7 = 469 \)).
- Continue this process to refine the quotient, resulting in approximately 37.947.
These methods provide quick and reasonably accurate approximations for the square root of 1440, useful in practical situations where exact values are not critical.
Square Root of 1440 in Various Fields
The square root of 1440, approximately 37.95, finds diverse applications across various fields. Here are some notable examples:
- Mathematics and Geometry:
In geometry, the square root is fundamental in calculating distances, areas, and in solving quadratic equations. For instance, the distance formula in a 2-dimensional space, derived from the Pythagorean theorem, often involves square roots:
\( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
- Engineering and Architecture:
Engineers use square roots to determine the natural frequency of structures, ensuring stability under different loads, such as wind or traffic vibrations. This is crucial for the design of safe and resilient buildings and bridges.
- Finance:
Square roots are used to calculate volatility in finance, helping investors assess the risk of stock investments. The standard deviation, a measure of volatility, is the square root of the variance.
\( \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \)
- Physics:
In physics, square roots are applied to calculate various properties such as the speed of waves and the intensity of sound and light waves. For example, the root-mean-square (RMS) value of alternating current (AC) is determined using square roots.
\( V_{RMS} = \sqrt{\frac{1}{T} \int_{0}^{T} [v(t)]^2 dt} \)
- Statistics:
In statistical analysis, the standard deviation, which measures data dispersion, is the square root of the variance. This metric is vital for interpreting data distributions and making informed decisions.
- Computer Science:
Square roots are integral to algorithms in computer graphics for calculating distances and rendering realistic images. They are also used in encryption algorithms for secure data transmission.
- Navigation:
Navigation systems use square roots to calculate the shortest distance between two points on a map, aiding in route optimization for various transportation methods.
- Telecommunications:
In telecommunications, the inverse square law describes how signal strength decreases with distance, crucial for designing effective communication networks.
Practical Examples and Use Cases
The square root of 1440, approximately 37.95, finds applications across various fields. Here are some practical examples and use cases:
-
Architecture and Engineering:
In structural engineering, the square root is often used to calculate the natural frequencies of buildings and bridges. For instance, when assessing the vibrations and stability of a bridge, engineers might use the square root of values related to the load and material properties.
-
Finance:
Square roots are used in finance to calculate the standard deviation of investment returns, which is crucial for assessing the risk associated with a particular investment. For example, the square root of the variance gives the standard deviation, helping investors understand the volatility of stock prices.
-
Physics:
In physics, the square root function is used in formulas involving waves and oscillations. For example, the formula for the period of a pendulum includes the square root of the length of the pendulum divided by the acceleration due to gravity.
-
Geometry:
Square roots are essential in geometry, particularly when dealing with right triangles and the Pythagorean theorem. For instance, if a right triangle has legs of lengths 7 and 24 units, the length of the hypotenuse can be found using the square root of the sum of the squares of the legs: √(7² + 24²) = √625 = 25 units.
-
Computer Graphics:
In computer graphics, calculating distances between points in 2D or 3D space often involves square roots. For example, the distance between points (x1, y1) and (x2, y2) is calculated as √((x2 - x1)² + (y2 - y1)²).
-
Cryptography:
Square roots play a role in cryptographic algorithms, particularly in methods used for encryption and decryption. For example, some public key cryptography systems use square roots in the generation of keys and in the encryption process itself.
-
Navigation:
In navigation, the square root is used to calculate distances between coordinates. For instance, the distance between two points on a map is determined using the Euclidean distance formula, which involves taking the square root of the sum of the squares of the differences in the coordinates.
Visual Representation and Graphs
The square root of 1440 can be visualized and represented graphically in various ways. Graphing the function \( y = \sqrt{x} \) provides insights into the nature of square roots and their properties.
Graph of the Square Root Function
The function \( y = \sqrt{x} \) is defined for all non-negative values of \( x \). Its graph is a curve that starts at the origin (0,0) and increases slowly, forming a shape similar to the top half of a parabola rotated 90 degrees.
- For \( x = 0 \), \( y = \sqrt{0} = 0 \).
- For \( x = 1 \), \( y = \sqrt{1} = 1 \).
- For \( x = 4 \), \( y = \sqrt{4} = 2 \).
- For \( x = 9 \), \( y = \sqrt{9} = 3 \).
- For \( x = 16 \), \( y = \sqrt{16} = 4 \).
The graph can be plotted using these points, showing the increasing nature of the function.
Graphical Analysis of the Square Root of 1440
To visualize the square root of 1440, we can use the graph of \( y = \sqrt{x} \). Although 1440 is not a perfect square, we can approximate its square root:
Since \( \sqrt{1440} \approx 37.95 \), on the graph, we locate \( x = 1440 \) and find the corresponding \( y \) value, which will be slightly less than 38.
Visualizing Transformations
Transformations of the square root function can help in understanding its behavior. For example:
- Vertical Shift: \( y = \sqrt{x} + k \) shifts the graph up by \( k \) units.
- Horizontal Shift: \( y = \sqrt{x - h} \) shifts the graph right by \( h \) units.
- Vertical Stretch/Compression: \( y = a\sqrt{x} \) stretches the graph vertically by a factor of \( a \).
These transformations help in graphing more complex square root functions and analyzing their properties.
Graphical Tools and Software
Various tools can be used to graph square root functions, such as:
- Graphing Calculators: Devices like the TI-84 can graph \( y = \sqrt{x} \) and its transformations.
- Software: Programs like GeoGebra and Desmos provide interactive platforms for graphing and exploring mathematical functions.
- Online Resources: Websites like Khan Academy offer tutorials and interactive graphs to understand square root functions better.
Using these tools, we can visualize and analyze the square root of 1440 effectively, gaining deeper insights into its mathematical properties.
Frequently Asked Questions
-
What is the square root of 1440?
The square root of 1440 is \(12\sqrt{10}\), which approximately equals 37.95.
-
How do you calculate the square root of 1440?
The square root of 1440 can be calculated using various methods such as the prime factorization method, long division method, or using a calculator. For example, using a calculator, you would simply enter 1440 and press the square root button.
-
What is the simplified form of the square root of 1440?
The simplified form of the square root of 1440 is \(12\sqrt{10}\).
-
Is the square root of 1440 a rational number?
No, the square root of 1440 is an irrational number because it cannot be expressed as a simple fraction.
-
How do you represent the square root of 1440 in exponential form?
The square root of 1440 in exponential form is \(1440^{0.5}\).
-
What are some approximation techniques for finding the square root of 1440?
Some approximation techniques include the use of iterative methods like the Newton-Raphson method or by using simpler methods such as averaging. For example, an initial guess can be refined by iteratively averaging the guess with 1440 divided by the guess.
Conclusion and Summary
The square root of 1440 is a fascinating mathematical concept with various applications and properties. The value of the square root of 1440 is approximately 37.947. This value is significant because it is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form is non-terminating and non-repeating.
Throughout this exploration, we have delved into different methods to calculate the square root, including the prime factorization and long division methods. These methods help in understanding the underlying structure and complexity of the number.
The historical context and applications of the square root of 1440 show its relevance in various fields such as architecture, engineering, and computer science. Approximation techniques, including numerical methods and iterative algorithms, provide ways to estimate the square root with high precision.
Visual representations and graphs further aid in comprehending the behavior and properties of the square root of 1440, allowing for a more intuitive understanding of its value and significance.
In practical examples and use cases, the square root of 1440 is applied in real-world scenarios, demonstrating its importance in solving equations, calculating dimensions, and optimizing solutions.
In conclusion, the square root of 1440 is more than just a number; it is a concept that bridges various aspects of mathematics and its applications. Understanding this number enriches our appreciation of mathematical principles and their practical implications.
READ MORE:
Video hướng dẫn cách tìm căn bậc hai bằng phương pháp chia, giúp bạn dễ dàng hiểu và áp dụng phương pháp này.
Tìm Căn Bậc Hai Bằng Phương Pháp Chia