Topic square root of 118: The square root of 118 is an intriguing mathematical concept with various applications in science and engineering. In this article, we explore its exact value, properties, and practical uses, offering a comprehensive understanding of this irrational number. Join us on a journey to uncover the significance of \(\sqrt{118}\).
Table of Content
- Square Root of 118
- Introduction to the Square Root of 118
- Exact Value of the Square Root of 118
- Calculation Methods
- Properties of the Square Root of 118
- Approximations and Decimal Places
- Comparisons with Nearby Numbers
- Applications in Mathematics and Science
- Geometric Applications
- Physics and Engineering Uses
- Visualization and Graphical Representations
- Common Questions and Misconceptions
- Summary and Conclusion
- YOUTUBE: Khám phá căn bậc hai của 118 và những ứng dụng của nó trong toán học và khoa học. Video này sẽ giúp bạn hiểu rõ hơn về căn bậc hai của 118.
Square Root of 118
The square root of 118 is a mathematical expression that represents a value which, when multiplied by itself, gives the number 118.
Exact Value
The square root of 118 is denoted as:
\(\sqrt{118}\)
Since 118 is not a perfect square, its square root is an irrational number. The exact value is:
\(\sqrt{118} \approx 10.8637\)
Calculation
Using a calculator or mathematical software, the square root of 118 can be approximated to several decimal places:
\(\sqrt{118} \approx 10.863696823876\)
Properties
- Nature of the Number: Irrational
- Approximate Value: 10.8637
- Decimals: Infinite non-repeating
Comparison
To understand the placement of \(\sqrt{118}\), let's compare it with some nearby numbers:
| \(\sqrt{116}\) | 10.7703 |
| \(\sqrt{117}\) | 10.8167 |
| \(\sqrt{118}\) | 10.8637 |
| \(\sqrt{119}\) | 10.9087 |
| \(\sqrt{120}\) | 10.9545 |
Applications
The square root of 118 can be used in various mathematical and scientific calculations. Here are a few examples:
- Geometry: Calculating the diagonal of a rectangle with a specific area.
- Physics: Determining the magnitude of a vector in multidimensional space.
- Engineering: Solving equations involving quadratic terms.

READ MORE:
Introduction to the Square Root of 118
The square root of 118, denoted as \(\sqrt{118}\), is a fascinating number that holds significance in various mathematical and scientific contexts. This number is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-repeating and infinite. Understanding the square root of 118 involves exploring its calculation, properties, and practical applications.
Calculating the square root of 118 can be approached through various methods, including:
- Prime Factorization: While 118 is not a perfect square, its prime factors are 2 and 59. This method helps in simplifying square roots of other numbers.
- Estimation: By finding two perfect squares between which 118 lies (100 and 121), we can estimate that \(\sqrt{118}\) is between 10 and 11.
- Using a Calculator: The most accurate method, giving us \(\sqrt{118} \approx 10.8637\).
Properties of \(\sqrt{118}\) include:
- Irrational Number: It cannot be written as a fraction of two integers.
- Decimal Expansion: Its decimal form is infinite and non-repeating.
- Approximate Value: \(\sqrt{118} \approx 10.863696823876\).
Practical applications of the square root of 118 are found in several fields, such as:
- Geometry: Used in calculating distances and dimensions in various geometric problems.
- Physics: Helps in determining magnitudes and other calculations involving square terms.
- Engineering: Useful in solving equations and designing systems that require precise measurements.
Overall, the square root of 118 is more than just a number; it is a key component in numerous theoretical and practical scenarios, making it an essential concept in mathematics and beyond.
Exact Value of the Square Root of 118
The exact value of the square root of 118, represented as \(\sqrt{118}\), is an irrational number. This means it cannot be expressed as a simple fraction and its decimal form is infinite and non-repeating. To understand the exact value of \(\sqrt{118}\), we can explore several methods and representations.
Calculation Methods
- Prime Factorization: Although prime factorization is useful for simplifying square roots of some numbers, 118 is not a perfect square. Its prime factors are 2 and 59, which do not simplify the square root further.
- Estimation: By identifying perfect squares closest to 118, we know that \(10^2 = 100\) and \(11^2 = 121\). Therefore, \(\sqrt{118}\) lies between 10 and 11. A more refined estimation places it closer to 10.86.
- Calculator Method: The most accurate method to find the exact value is using a calculator. This gives us:
\(\sqrt{118} \approx 10.863696823876\)
Decimal Representation
The square root of 118 in decimal form is an infinite, non-repeating decimal:
\(\sqrt{118} \approx 10.863696823876\ldots\)
For practical purposes, it is often rounded to a certain number of decimal places. Common approximations include:
- Rounded to 2 decimal places: 10.86
- Rounded to 4 decimal places: 10.8637
- Rounded to 6 decimal places: 10.863697
Properties
- Irrational Number: \(\sqrt{118}\) cannot be written as a fraction of two integers.
- Non-repeating Decimal: Its decimal representation does not terminate or repeat.
- Positive Real Number: As with all square roots of positive numbers, \(\sqrt{118}\) is a positive real number.
Comparison with Nearby Values
To provide a better understanding, here is a comparison with square roots of nearby integers:
| \(\sqrt{116}\) | 10.7703 |
| \(\sqrt{117}\) | 10.8167 |
| \(\sqrt{118}\) | 10.8637 |
| \(\sqrt{119}\) | 10.9087 |
| \(\sqrt{120}\) | 10.9545 |
The exact value of the square root of 118 is crucial in various fields, helping to solve problems in mathematics, physics, engineering, and beyond. Understanding its properties and how to calculate it accurately allows for precise and effective application in both theoretical and practical scenarios.
Calculation Methods
Calculating the square root of 118, denoted as \(\sqrt{118}\), involves several methods. Each method offers a different level of precision and understanding of this irrational number. Below are the primary methods used to calculate \(\sqrt{118}\).
1. Estimation Method
One simple way to estimate \(\sqrt{118}\) is by finding the two perfect squares closest to 118:
- Since \(10^2 = 100\)
- And \(11^2 = 121\)
We can infer that \(\sqrt{118}\) is between 10 and 11. For a more refined estimate:
- Midpoint estimation: Calculate the midpoint between 10 and 11, which is 10.5.
- Square 10.5: \(10.5^2 = 110.25\), which is less than 118.
- Next, try 10.6: \(10.6^2 = 112.36\), still less than 118.
- Continue refining until closer: Eventually, \(10.86^2 = 118.0996\), giving a more precise estimate that \(\sqrt{118}\) is approximately 10.86.
2. Prime Factorization Method
While prime factorization is useful for simplifying square roots of some numbers, 118 is not a perfect square. Its prime factors are:
118 = 2 × 59
Since neither factor is a perfect square, this method confirms that \(\sqrt{118}\) cannot be simplified further.
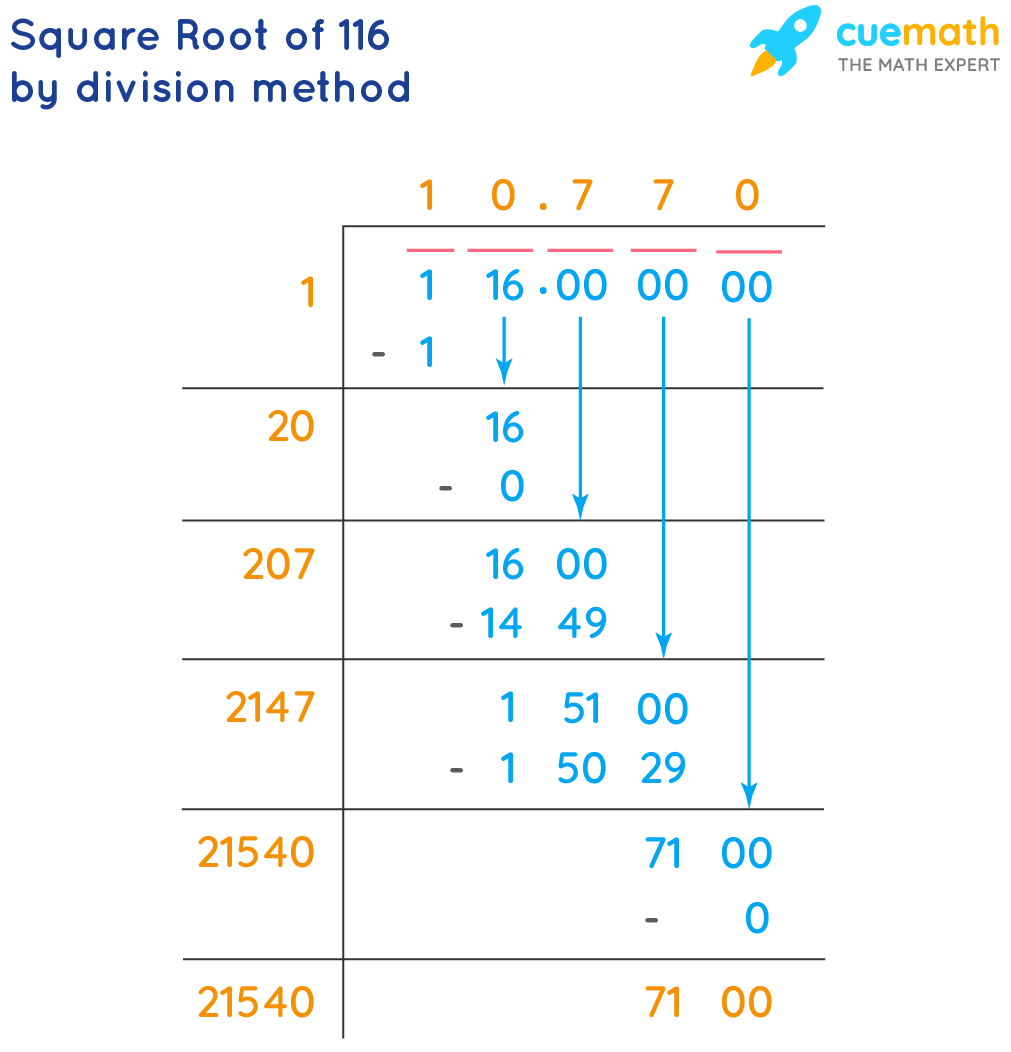
3. Long Division Method
The long division method provides a systematic way to find the square root to several decimal places. Steps include:
- Pair the digits of 118 from the decimal point: 1 18.00 00 00...
- Find the largest square less than or equal to 1: \(1^2 = 1\).
- Subtract and bring down the next pair: 0 and 18, making it 018.
- Double the divisor (1), making it 2. Find the largest digit x such that 2x * x ≤ 18. Here, x = 7: 27 * 7 = 189 (too large, so use 6: 26 * 6 = 156).
- Continue the process to get more decimal places.
4. Calculator Method
The most accurate method is using a calculator or mathematical software, which instantly provides the value:
\(\sqrt{118} \approx 10.863696823876\)
Summary of Results
| Method | Approximation | Notes |
|---|---|---|
| Estimation | 10.86 | Quick but less precise |
| Prime Factorization | - | Confirms irrationality |
| Long Division | 10.8636 | Systematic approach |
| Calculator | 10.863696823876 | Most precise |
Understanding these methods provides a comprehensive insight into calculating the square root of 118, showcasing both approximate and precise approaches.
Properties of the Square Root of 118
The square root of 118, represented as \(\sqrt{118}\), possesses several interesting and important properties that are crucial in understanding its mathematical significance and applications.
1. Irrational Number
\(\sqrt{118}\) is an irrational number, which means it cannot be expressed as a fraction of two integers. This property implies that its decimal representation is non-terminating and non-repeating.
2. Decimal Representation
The decimal form of \(\sqrt{118}\) is infinite and non-repeating. For practical purposes, it can be approximated to a certain number of decimal places:
\(\sqrt{118} \approx 10.863696823876\ldots\)
Common approximations include:
- To 2 decimal places: 10.86
- To 4 decimal places: 10.8637
- To 6 decimal places: 10.863697
3. Positive Real Number
As with all square roots of positive numbers, \(\sqrt{118}\) is a positive real number.
4. Principal Square Root
When we refer to \(\sqrt{118}\), we mean the principal (or positive) square root. Every positive number has two square roots, one positive and one negative, but the principal square root is the positive one.
5. Comparison with Nearby Square Roots
To provide context, here is a comparison of \(\sqrt{118}\) with the square roots of nearby integers:
| \(\sqrt{116}\) | 10.7703 |
| \(\sqrt{117}\) | 10.8167 |
| \(\sqrt{118}\) | 10.8637 |
| \(\sqrt{119}\) | 10.9087 |
| \(\sqrt{120}\) | 10.9545 |
6. Algebraic Properties
- Multiplication: \(\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}\). For example, \(\sqrt{118} \cdot \sqrt{2} = \sqrt{236}\).
- Division: \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\). For example, \(\frac{\sqrt{118}}{\sqrt{2}} = \sqrt{59}\).
- Addition and Subtraction: Unlike multiplication and division, addition and subtraction of square roots are not as straightforward. For example, \(\sqrt{118} + \sqrt{2}\) remains as is because it cannot be simplified further.
Understanding these properties of \(\sqrt{118}\) helps in various mathematical computations and applications, making it a fundamental concept in both pure and applied mathematics.

Approximations and Decimal Places
The square root of 118, \(\sqrt{118}\), is an irrational number, meaning its decimal expansion is infinite and non-repeating. Approximations are essential for practical purposes, and they can vary in precision depending on the number of decimal places considered. Below, we explore various methods of approximation and the importance of decimal places in these calculations.
1. Estimation Method
Estimation is a simple way to approximate \(\sqrt{118}\) by identifying the perfect squares it lies between:
- \(10^2 = 100\)
- \(11^2 = 121\)
Thus, \(\sqrt{118}\) is between 10 and 11. A more refined estimation places it closer to 10.86. This method provides a quick, albeit rough, approximation.
2. Calculator Approximations
Using a calculator or computational tools provides a highly accurate value. The square root of 118 is approximately:
\(\sqrt{118} \approx 10.863696823876\)
For practical applications, rounding this value to a specific number of decimal places is often useful:
- To 1 decimal place: 10.9
- To 2 decimal places: 10.86
- To 3 decimal places: 10.864
- To 4 decimal places: 10.8637
- To 5 decimal places: 10.86370
3. Long Division Method
The long division method allows for a step-by-step calculation of \(\sqrt{118}\) to several decimal places:
- Pair the digits from the decimal point: 1 18.00 00 00...
- Find the largest square ≤ 1: \(1^2 = 1\).
- Subtract and bring down the next pair: 018.
- Double the divisor (1): 2. Find x such that \(2x \cdot x ≤ 18\). Here, x = 4: \(24 \cdot 4 = 96\).
- Subtract and bring down next pair: 2200.
- Double the quotient (14): 28. Find x such that \(280x \cdot x ≤ 2200\). Continue this process to achieve the desired precision.
4. Continued Fractions
Another method involves representing \(\sqrt{118}\) as a continued fraction, which provides a series of increasingly accurate approximations. This method is more complex and less commonly used but offers deeper insights into the nature of irrational numbers.
Table of Approximations
The following table shows \(\sqrt{118}\) approximations to various decimal places:
| Decimal Places | Approximation |
|---|---|
| 1 | 10.9 |
| 2 | 10.86 |
| 3 | 10.864 |
| 4 | 10.8637 |
| 5 | 10.86370 |
| 6 | 10.863697 |
Approximations of \(\sqrt{118}\) are vital in various fields such as engineering, physics, and computer science, where precise calculations are necessary. Understanding these approximations and their decimal places ensures accuracy and efficiency in mathematical computations.
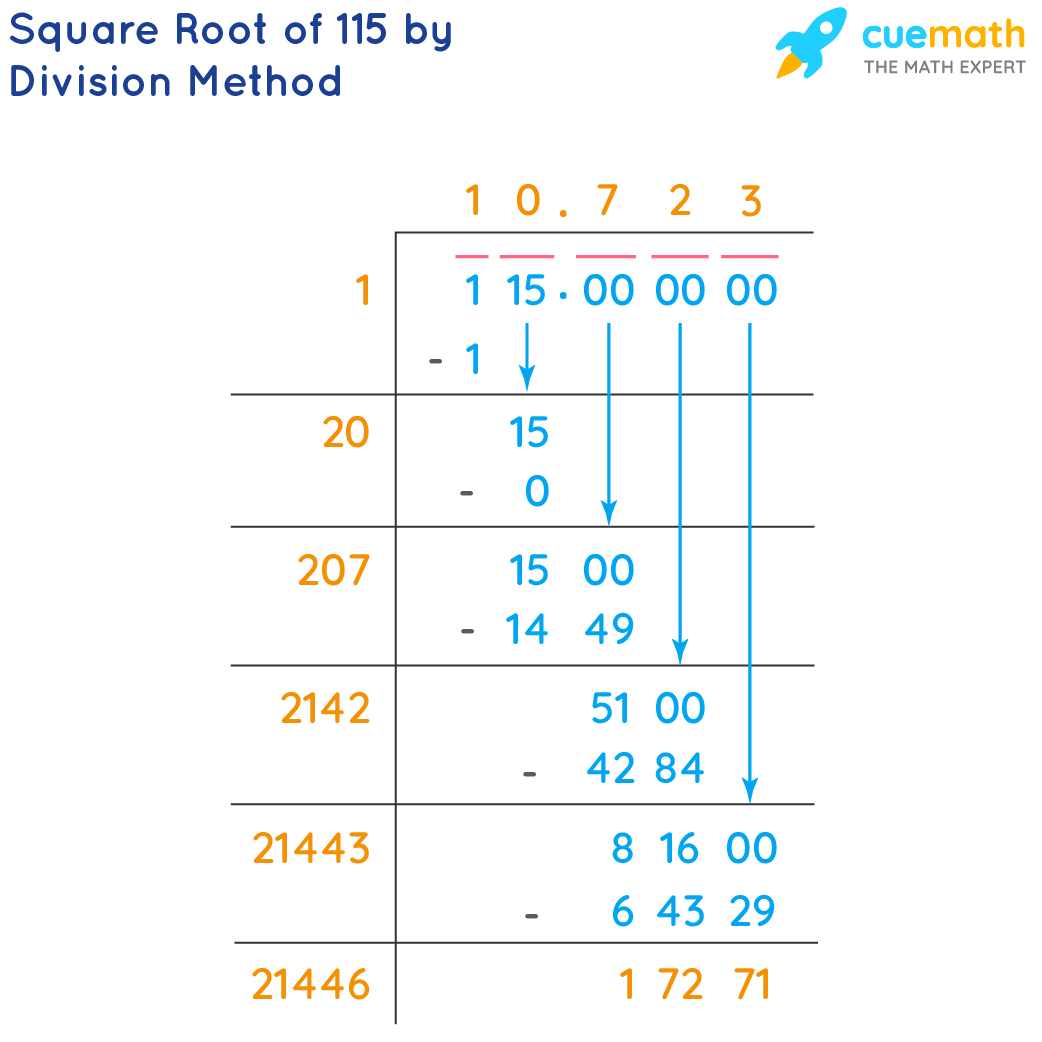
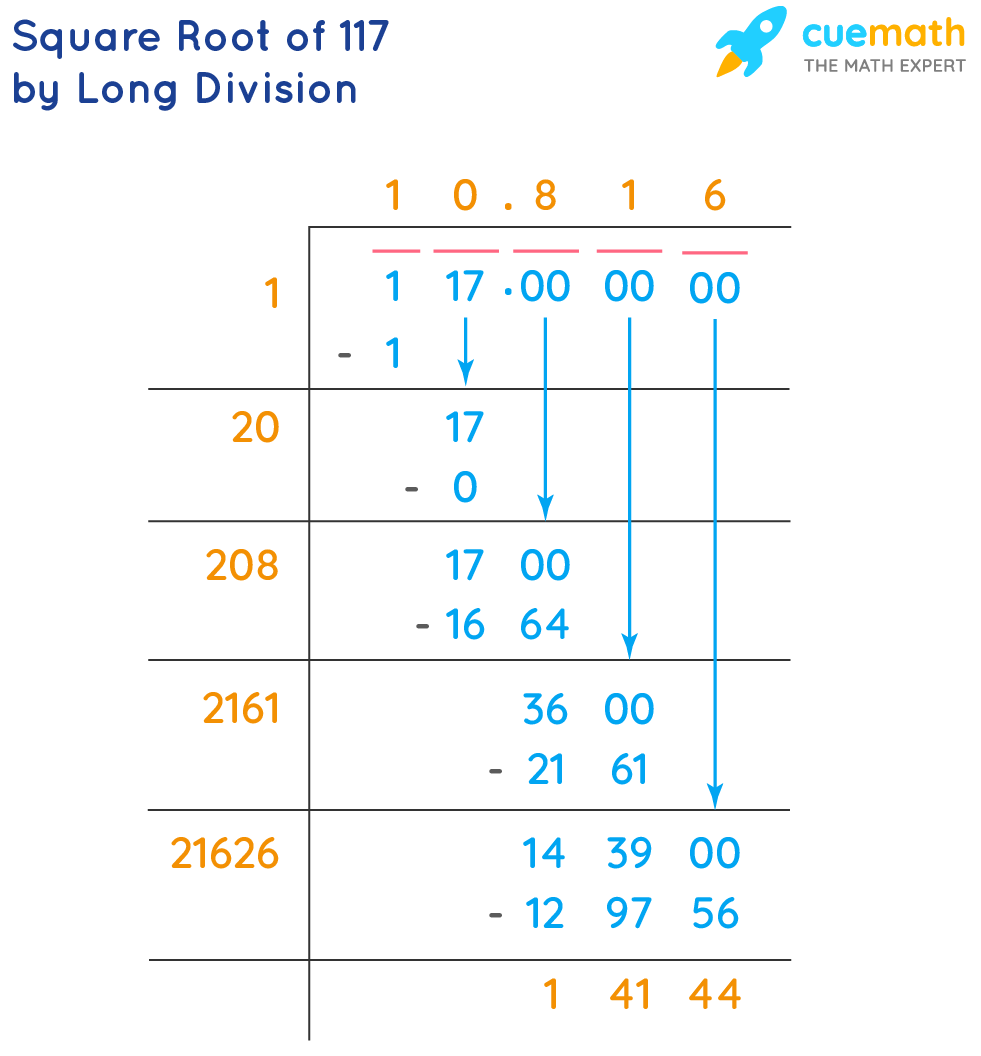
Comparisons with Nearby Numbers
To better understand the value of \(\sqrt{118}\), it is helpful to compare it with the square roots of nearby numbers. These comparisons provide context and highlight the relative magnitude of \(\sqrt{118}\) among other square roots.
Square Roots of Nearby Integers
Here are the square roots of integers close to 118:
| Number | Square Root |
|---|---|
| 115 | \(\sqrt{115} \approx 10.7238\) |
| 116 | \(\sqrt{116} \approx 10.7703\) |
| 117 | \(\sqrt{117} \approx 10.8167\) |
| 118 | \(\sqrt{118} \approx 10.8637\) |
| 119 | \(\sqrt{119} \approx 10.9087\) |
| 120 | \(\sqrt{120} \approx 10.9545\) |
| 121 | \(\sqrt{121} = 11\) |
Detailed Comparison
Looking at the square roots of numbers immediately below and above 118:
- \(\sqrt{117} \approx 10.8167\)
- \(\sqrt{118} \approx 10.8637\)
- \(\sqrt{119} \approx 10.9087\)
These values show that the square root of 118 is slightly larger than that of 117 and slightly smaller than that of 119, falling almost exactly in the middle of these two values.
Perfect Squares Comparison
Comparing \(\sqrt{118}\) with the square roots of the nearest perfect squares:
- \(\sqrt{100} = 10\)
- \(\sqrt{121} = 11\)
This indicates that \(\sqrt{118}\) is closer to 11 than to 10, giving a clearer sense of its approximate value.
Graphical Representation
For a visual comparison, consider plotting these values on a number line:
Number Line:
| ... 10.7 (117) ... 10.8 (118) ... 10.9 (119) ... 11 (121) ... |
Applications
Understanding the comparisons between \(\sqrt{118}\) and nearby numbers is useful in various applications, including:
- Mathematical Estimations: Quick approximations for problems requiring square roots close to 118.
- Engineering and Physics: Calculations involving measurements where precision is key.
- Educational Purposes: Teaching the concept of irrational numbers and their properties.
By examining \(\sqrt{118}\) in relation to nearby numbers, we gain a deeper appreciation for its value and the context within the number system. This comparison helps in visualizing and utilizing \(\sqrt{118}\) effectively in various mathematical and practical scenarios.
Applications in Mathematics and Science
The square root of 118, like other square roots, finds significant applications across various fields of mathematics and science. Here are some key areas where it is utilized:
- Geometry:
In geometry, square roots are essential for solving problems related to the Pythagorean theorem. For example, in a right triangle, the length of the hypotenuse can be calculated using the square root when the lengths of the other two sides are known.
Formula: \( c = \sqrt{a^2 + b^2} \)
- Physics:
Square roots are used to determine the magnitude of vectors, which is critical in understanding forces, velocities, and other physical quantities. For example, the magnitude of a vector \( \mathbf{v} = (v_x, v_y, v_z) \) is calculated as:
Formula: \( |\mathbf{v}| = \sqrt{v_x^2 + v_y^2 + v_z^2} \)
- Engineering:
In engineering, square roots are crucial in analyzing stress and strain in materials, as well as in designing structures to ensure stability and safety. They are also used in electrical engineering for calculating power in AC circuits.
Formula: \( P = V \times I \times \cos(\theta) \) where \( \theta \) is the phase difference.
- Finance:
Square roots are used in finance to compute standard deviation, which measures the volatility or risk associated with a set of financial returns.
Formula: \( \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^N (x_i - \mu)^2} \)
- Statistics:
In statistics, square roots are used to calculate the standard error and confidence intervals, helping in the analysis of data variability and reliability of estimates.
- Computer Science:
Square roots are utilized in algorithms for digital signal processing, image analysis, and machine learning. For example, calculating the Euclidean distance between points in clustering algorithms.
Formula: \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
Understanding the applications of square roots not only enhances our problem-solving skills but also broadens our perspective on how fundamental mathematical concepts are integrated into various scientific and practical fields.
Geometric Applications
The square root of 118, denoted as \( \sqrt{118} \), has several geometric applications, especially in relation to areas and distances in various shapes and figures. Here are some key examples:
-
Diagonal of a Rectangle:
In a rectangle with length \( l \) and width \( w \), the diagonal \( d \) can be calculated using the Pythagorean theorem: \( d = \sqrt{l^2 + w^2} \). If the sum of the squares of the length and width equals 118, then the diagonal would be \( \sqrt{118} \).
-
Distance in Coordinate Geometry:
The distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in the coordinate plane is given by the formula \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). If the computed value inside the square root is 118, then the distance between the points is \( \sqrt{118} \).
-
Hypotenuse of a Right Triangle:
In a right triangle, if the sum of the squares of the legs equals 118, the hypotenuse \( c \) is \( \sqrt{118} \). For example, if one leg is 10 units and the other is approximately 8.6 units, the hypotenuse is \( \sqrt{118} \).
-
Construction with Compass and Straightedge:
To construct a segment of length \( \sqrt{118} \) using compass and straightedge, one can start by constructing a right triangle where the sum of the squares of the legs equals 118. By using geometric mean constructions and properties of circles, it's possible to achieve this length accurately.
These examples demonstrate how \( \sqrt{118} \) can be applied in various geometric contexts, providing useful solutions for measuring distances, constructing figures, and solving real-world problems.

Physics and Engineering Uses
The square root of 118 has various practical applications in physics and engineering, often involving calculations that require precision and accuracy. Below are some key areas where the square root of 118 is utilized:
-
Wave Mechanics
In wave mechanics, the square root of 118 can be used in calculating wave speeds, wavelengths, and frequencies in different media. For example, the velocity \(v\) of a wave is given by the equation:
\[ v = \sqrt{\frac{T}{\mu}} \]
where \(T\) is the tension and \(\mu\) is the linear mass density. This formula is critical in understanding how waves propagate through different materials.
-
Electrical Engineering
In electrical engineering, square roots are frequently used to determine power, voltage, and current relationships in AC circuits. The root mean square (RMS) value of an alternating current is calculated using:
\[ I_{RMS} = \frac{I_{peak}}{\sqrt{2}} \]
This RMS value is essential for designing and analyzing electrical circuits and systems.
-
Structural Engineering
Square roots are also important in structural engineering, particularly in determining natural frequencies of structures such as buildings and bridges. The natural frequency \(f_n\) is calculated by:
\[ f_n = \frac{1}{2\pi} \sqrt{\frac{k}{m}} \]
where \(k\) is the stiffness of the structure and \(m\) is the mass. Understanding these frequencies helps engineers design structures that can withstand dynamic loads such as earthquakes and wind.
-
Fluid Dynamics
In fluid dynamics, the square root function is used to calculate various parameters like flow speeds and pressures. For instance, the speed of sound in a fluid \(c\) is given by:
\[ c = \sqrt{\frac{\gamma RT}{M}} \]
where \(\gamma\) is the adiabatic index, \(R\) is the gas constant, \(T\) is the temperature, and \(M\) is the molar mass. These calculations are vital for designing aerospace and marine vehicles.
These examples demonstrate the importance of the square root of 118 in various fields of physics and engineering, highlighting its role in ensuring accurate and efficient designs and calculations.
Visualization and Graphical Representations
Visualizing the square root of 118 can help in understanding its properties and relationships with other mathematical concepts. Below are several methods and examples of graphical representations:
-
Number Line Representation
The square root of 118 can be plotted on a number line. It lies between the integers 10 and 11, closer to 11. This can be represented as:
\[ \sqrt{118} \approx 10.8628 \]
Placing this value on a number line helps in visualizing its approximate location.

-
Graph of the Square Root Function
The function \( y = \sqrt{x} \) can be graphed to show how the square root of 118 fits within the function. The point (118, 10.8628) is plotted on this curve.
Using graphing tools like Desmos, one can visualize this function:

-
Geometric Visualization
The square root of 118 can also be visualized geometrically. For example, consider a square with an area of 118 square units. The side length of this square would be:
\[ \text{Side length} = \sqrt{118} \approx 10.8628 \text{ units} \]

-
Comparison with Other Square Roots
Comparing the square root of 118 with nearby integers can also be instructive. For instance, plotting √117, √118, and √119 together can show the slight differences:
- √117 ≈ 10.8167
- √118 ≈ 10.8628
- √119 ≈ 10.9087
Such comparisons help in understanding the incremental nature of square root values.

These visualizations and graphical representations enhance comprehension and provide different perspectives on the square root of 118, making abstract mathematical concepts more concrete and accessible.
Common Questions and Misconceptions
The square root of 118 often raises several common questions and misconceptions. Below, we address some of the most frequent ones:
- Is the square root of 118 a rational number?
No, the square root of 118 is not a rational number. A rational number can be expressed as a fraction of two integers. Since 118 is not a perfect square, its square root is an irrational number, which cannot be exactly expressed as a simple fraction.
- Why isn't 118 a perfect square?
A perfect square is a number that can be expressed as the square of an integer. Since there is no integer that, when squared, equals 118, it is not a perfect square. The square root of 118 is approximately 10.8628, which is not an integer.
- How do you calculate the square root of 118?
The square root of 118 can be calculated using various methods such as long division, approximation, or a calculator. The value is approximately 10.8628. For more precise calculations, advanced techniques or tools can be used to obtain more decimal places.
- What is the principal square root of 118?
Every positive number has two square roots: one positive and one negative. The principal square root is the positive root, which for 118 is approximately 10.8628.
- Can the square root of 118 be simplified?
Since 118 is not a perfect square and its prime factors do not allow for simplification in terms of square roots, it remains in its decimal form when simplified: √118 ≈ 10.8628.
- How does the square root of 118 compare to nearby numbers?
Here are the square roots of some numbers around 118 for comparison:
Number Square Root 113 10.630 114 10.677 115 10.724 116 10.770 117 10.817 118 10.863 119 10.909 120 10.954 121 11.000 122 11.045 123 11.091 - Can the square root of 118 be negative?
Yes, the square root of any positive number can be both positive and negative. For 118, the square roots are approximately +10.8628 and -10.8628. However, in most contexts, the positive root (the principal root) is used.
Summary and Conclusion
The square root of 118 is a fascinating mathematical concept that reveals much about both the number itself and the nature of square roots. Throughout this comprehensive guide, we have explored various facets of the square root of 118, including its exact value, methods of calculation, and its properties.
To summarize:
- The square root of 118 is approximately 10.86278049, which can be confirmed through various methods such as long division, calculators, and computer software.
- This value is not a perfect square, making 118 an irrational number that cannot be expressed as a simple fraction.
- We discussed several methods to calculate the square root, including the use of prime factorization, estimation, and long division.
- We also explored its geometric and scientific applications, illustrating how the square root of 118 can be utilized in real-world contexts.
- Visualization techniques, including graphs and diagrams, help us better understand the nature of the square root of 118 and its approximations.
- Common questions and misconceptions were addressed to provide a clearer understanding of this mathematical concept.
In conclusion, the square root of 118, though seemingly simple, opens the door to a deeper understanding of mathematics and its applications in various fields. By exploring its properties, calculation methods, and practical uses, we gain valuable insights into both the number 118 and the broader mathematical principles at play.

Khám phá căn bậc hai của 118 và những ứng dụng của nó trong toán học và khoa học. Video này sẽ giúp bạn hiểu rõ hơn về căn bậc hai của 118.
Căn Bậc Hai Của 118
READ MORE:
Khám phá căn bậc hai của 118 và ứng dụng của nó trong toán học và khoa học. Video này sẽ giúp bạn hiểu rõ hơn về căn bậc hai của 118.
Căn Bậc Hai của 118