Topic square root of 1 to 100: Discover the fascinating world of square roots with our comprehensive guide, covering the square root of numbers from 1 to 100. Learn how to calculate, apply, and understand the significance of square roots in various fields. Perfect for students, educators, and math enthusiasts looking to deepen their knowledge and skills.
Table of Content
- Square Roots of Numbers from 1 to 100
- Introduction
- What is a Square Root?
- Properties of Square Roots
- Calculating Square Roots
- Square Roots Table: 1 to 100
- Methods to Find Square Roots
- Applications of Square Roots
- Square Roots in Real Life
- Square Roots and Geometry
- Common Square Roots
- Square Roots and Algebra
- Historical Significance of Square Roots
- Tips for Learning Square Roots
- Practice Problems
- FAQs about Square Roots
- Conclusion
- YOUTUBE:
Square Roots of Numbers from 1 to 100
The square root of a number is a value that, when multiplied by itself, gives the original number. Below is a detailed list of the square roots of numbers from 1 to 100.
Square Roots List
- \(\sqrt{1} = 1\)
- \(\sqrt{2} \approx 1.414\)
- \(\sqrt{3} \approx 1.732\)
- \(\sqrt{4} = 2\)
- \(\sqrt{5} \approx 2.236\)
- \(\sqrt{6} \approx 2.449\)
- \(\sqrt{7} \approx 2.646\)
- \(\sqrt{8} \approx 2.828\)
- \(\sqrt{9} = 3\)
- \(\sqrt{10} \approx 3.162\)
- \(\sqrt{11} \approx 3.317\)
- \(\sqrt{12} \approx 3.464\)
- \(\sqrt{13} \approx 3.606\)
- \(\sqrt{14} \approx 3.742\)
- \(\sqrt{15} \approx 3.873\)
- \(\sqrt{16} = 4\)
- \(\sqrt{17} \approx 4.123\)
- \(\sqrt{18} \approx 4.243\)
- \(\sqrt{19} \approx 4.359\)
- \(\sqrt{20} \approx 4.472\)
- \(\sqrt{21} \approx 4.583\)
- \(\sqrt{22} \approx 4.690\)
- \(\sqrt{23} \approx 4.796\)
- \(\sqrt{24} \approx 4.899\)
- \(\sqrt{25} = 5\)
- \(\sqrt{26} \approx 5.099\)
- \(\sqrt{27} \approx 5.196\)
- \(\sqrt{28} \approx 5.291\)
- \(\sqrt{29} \approx 5.385\)
- \(\sqrt{30} \approx 5.477\)
- \(\sqrt{31} \approx 5.568\)
- \(\sqrt{32} \approx 5.657\)
- \(\sqrt{33} \approx 5.745\)
- \(\sqrt{34} \approx 5.831\)
- \(\sqrt{35} \approx 5.916\)
- \(\sqrt{36} = 6\)
- \(\sqrt{37} \approx 6.083\)
- \(\sqrt{38} \approx 6.164\)
- \(\sqrt{39} \approx 6.245\)
- \(\sqrt{40} \approx 6.325\)
- \(\sqrt{41} \approx 6.403\)
- \(\sqrt{42} \approx 6.481\)
- \(\sqrt{43} \approx 6.557\)
- \(\sqrt{44} \approx 6.633\)
- \(\sqrt{45} \approx 6.708\)
- \(\sqrt{46} \approx 6.782\)
- \(\sqrt{47} \approx 6.856\)
- \(\sqrt{48} \approx 6.928\)
- \(\sqrt{49} = 7\)
- \(\sqrt{50} \approx 7.071\)
- \(\sqrt{51} \approx 7.141\)
- \(\sqrt{52} \approx 7.211\)
- \(\sqrt{53} \approx 7.280\)
- \(\sqrt{54} \approx 7.348\)
- \(\sqrt{55} \approx 7.416\)
- \(\sqrt{56} \approx 7.483\)
- \(\sqrt{57} \approx 7.550\)
- \(\sqrt{58} \approx 7.616\)
- \(\sqrt{59} \approx 7.681\)
- \(\sqrt{60} \approx 7.746\)
- \(\sqrt{61} \approx 7.810\)
- \(\sqrt{62} \approx 7.874\)
- \(\sqrt{63} \approx 7.937\)
- \(\sqrt{64} = 8\)
- \(\sqrt{65} \approx 8.062\)
- \(\sqrt{66} \approx 8.124\)
- \(\sqrt{67} \approx 8.185\)
- \(\sqrt{68} \approx 8.246\)
- \(\sqrt{69} \approx 8.307\)
- \(\sqrt{70} \approx 8.366\)
- \(\sqrt{71} \approx 8.426\)
- \(\sqrt{72} \approx 8.485\)
- \(\sqrt{73} \approx 8.544\)
- \(\sqrt{74} \approx 8.602\)
- \(\sqrt{75} \approx 8.660\)
- \(\sqrt{76} \approx 8.718\)
- \(\sqrt{77} \approx 8.775\)
- \(\sqrt{78} \approx 8.832\)
- \(\sqrt{79} \approx 8.888\)
- \(\sqrt{80} \approx 8.944\)
- \(\sqrt{81} = 9\)
- \(\sqrt{82} \approx 9.055\)
- \(\sqrt{83} \approx 9.110\)
- \(\sqrt{84} \approx 9.165\)
- \(\sqrt{85} \approx 9.220\)
- \(\sqrt{86} \approx 9.274\)
- \(\sqrt{87} \approx 9.327\)
- \(\sqrt{88} \approx 9.381\)
- \(\sqrt{89} \approx 9.434\)
- \(\sqrt{90} \approx 9.487\)
- \(\sqrt{91} \approx 9.539\)
- \(\sqrt{92} \approx 9.592\)
- \(\sqrt{93} \approx 9.644\)
- \(\sqrt{94} \approx 9.695\)
- \(\sqrt{95} \approx 9.747\)
- \(\sqrt{96} \approx 9.798\)
- \(\sqrt{97} \approx 9.849\)
- \(\sqrt{98} \approx 9.899\)
- \(\sqrt{99} \approx 9.950\)
- \(\sqrt{100} = 10\)

READ MORE:
Introduction
Understanding the square root of numbers from 1 to 100 is fundamental in mathematics. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, \(\sqrt{25} = 5\) because \(5 \times 5 = 25\). This concept is essential for solving equations, understanding geometric properties, and various real-life applications.
Square roots are often represented using the radical symbol (√), and each number from 1 to 100 has a unique square root. While some square roots are whole numbers, others are irrational and continue indefinitely without repeating. Knowing how to calculate and approximate these values is crucial for academic and professional success in fields such as engineering, physics, and computer science.
Below, we provide a step-by-step approach to understanding and calculating the square roots of numbers from 1 to 100:
- Identify perfect squares (numbers whose square roots are whole numbers).
- Learn and use prime factorization for non-perfect squares.
- Use the long division method for manual calculation of square roots.
- Apply approximation techniques and tools for quick estimates.
- Understand the properties of square roots to simplify calculations.
Mastering these steps will enable you to calculate square roots efficiently and apply this knowledge in various mathematical contexts.
What is a Square Root?
A square root of a number is a value that, when multiplied by itself, results in the original number. It is denoted by the radical symbol (√). For example, the square root of 9 is 3, because \(3 \times 3 = 9\). In mathematical terms, if \(x^2 = y\), then \(x\) is the square root of \(y\).
Square roots can be classified into two categories:
- Perfect Squares: Numbers that have whole number square roots. Examples include \(\sqrt{1} = 1\), \(\sqrt{4} = 2\), \(\sqrt{9} = 3\), and so on.
- Non-Perfect Squares: Numbers that do not have whole number square roots and result in irrational numbers. Examples include \(\sqrt{2} \approx 1.414\), \(\sqrt{3} \approx 1.732\), \(\sqrt{5} \approx 2.236\), etc.
Here are some key properties of square roots:
- Non-Negative Results: Square roots of non-negative numbers are always non-negative. The principal square root is the non-negative root.
- Multiplication: The square root of a product is the product of the square roots: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).
- Division: The square root of a quotient is the quotient of the square roots: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- Exponents: The square root of a number can be expressed as an exponent: \(\sqrt{a} = a^{\frac{1}{2}}\).
Understanding these properties helps in simplifying complex mathematical expressions and solving various algebraic and geometric problems.
Properties of Square Roots
Square roots have several important properties that make them useful in various mathematical operations and problem-solving scenarios. Understanding these properties helps simplify expressions and perform calculations more efficiently.
Here are the key properties of square roots:
- Non-Negative Results: The principal square root of a non-negative number is always non-negative. For example, \(\sqrt{16} = 4\) and not -4, although both 4 and -4 are square roots of 16.
- Multiplicative Property: The square root of a product is equal to the product of the square roots of the factors. For example: \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \] This property holds for any non-negative numbers \(a\) and \(b\).
- Divisive Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator. For example: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] This property is applicable for any non-negative numbers \(a\) and \(b\), with \(b \neq 0\).
- Exponential Form: The square root of a number can be expressed as the number raised to the power of 1/2. For example: \[ \sqrt{a} = a^{\frac{1}{2}} \] This representation is useful in algebra and calculus for simplifying expressions and solving equations.
- Square of a Square Root: The square of the square root of a number returns the original number. For example: \[ (\sqrt{a})^2 = a \] This property highlights the inverse relationship between squaring a number and taking the square root.
- Additive Property: The square root of a sum is not generally equal to the sum of the square roots. For example: \[ \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \] This property indicates that square roots do not distribute over addition.
- Zero and One: The square root of zero is zero, and the square root of one is one: \[ \sqrt{0} = 0 \quad \text{and} \quad \sqrt{1} = 1 \] These are straightforward cases but important to remember in calculations.
By understanding and applying these properties, one can handle square root operations more effectively in various mathematical contexts.
Calculating Square Roots
Calculating square roots can be approached in various ways depending on the number and the desired level of precision. Here, we outline several methods to calculate square roots, from simple estimations to more precise algorithms.
Method 1: Estimation
For quick estimations, find the two closest perfect squares between which the number lies. For example, to estimate \(\sqrt{50}\), note that it lies between \(\sqrt{49} = 7\) and \(\sqrt{64} = 8\). Therefore, \(\sqrt{50}\) is slightly more than 7.
Method 2: Prime Factorization
Prime factorization involves expressing the number as a product of prime numbers. Pair the prime factors and take one from each pair. For example:
- Find the prime factorization of 36: \(36 = 2 \times 2 \times 3 \times 3\).
- Pair the prime factors: \((2 \times 2) \times (3 \times 3)\).
- Take one from each pair: \(2 \times 3 = 6\).
- Thus, \(\sqrt{36} = 6\).
Method 3: Long Division Method
The long division method is a manual algorithm for finding square roots to a high degree of precision. Here’s a step-by-step process:
- Group the digits in pairs starting from the decimal point.
- Find the largest number whose square is less than or equal to the first group. This is the first digit of the square root.
- Subtract the square of the first digit from the first group and bring down the next pair of digits.
- Double the first digit and find a new digit to append, which, when multiplied by the doubled number plus the new digit, is less than or equal to the current number.
- Repeat the process for the desired number of decimal places.
Method 4: Newton’s Method (Babylonian Method)
Newton’s Method is an iterative approach to approximate square roots. The formula is:
where \(S\) is the number whose square root you are finding, and \(x_n\) is the current approximation. For example, to find \(\sqrt{10}\):
- Start with an initial guess \(x_0\) (e.g., \(x_0 = 3\)).
- Apply the formula: \(x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667\).
- Repeat until the desired accuracy is achieved: \(x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) = 3.1623\).
Method 5: Using Calculators and Software
For practical purposes, calculators and software tools provide quick and accurate square root calculations. Simply input the number and use the square root function.
By mastering these methods, you can calculate square roots effectively for any number, enhancing your mathematical skills and problem-solving abilities.

Square Roots Table: 1 to 100
Below is a comprehensive table of the square roots of numbers from 1 to 100. This table helps in quick reference and is useful for various mathematical calculations and problem-solving tasks.
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| 6 | \(\sqrt{6} \approx 2.449\) |
| 7 | \(\sqrt{7} \approx 2.646\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 9 | \(\sqrt{9} = 3\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
| 11 | \(\sqrt{11} \approx 3.317\) |
| 12 | \(\sqrt{12} \approx 3.464\) |
| 13 | \(\sqrt{13} \approx 3.606\) |
| 14 | \(\sqrt{14} \approx 3.742\) |
| 15 | \(\sqrt{15} \approx 3.873\) |
| 16 | \(\sqrt{16} = 4\) |
| 17 | \(\sqrt{17} \approx 4.123\) |
| 18 | \(\sqrt{18} \approx 4.243\) |
| 19 | \(\sqrt{19} \approx 4.359\) |
| 20 | \(\sqrt{20} \approx 4.472\) |
| 21 | \(\sqrt{21} \approx 4.583\) |
| 22 | \(\sqrt{22} \approx 4.690\) |
| 23 | \(\sqrt{23} \approx 4.796\) |
| 24 | \(\sqrt{24} \approx 4.899\) |
| 25 | \(\sqrt{25} = 5\) |
| 26 | \(\sqrt{26} \approx 5.099\) |
| 27 | \(\sqrt{27} \approx 5.196\) |
| 28 | \(\sqrt{28} \approx 5.291\) |
| 29 | \(\sqrt{29} \approx 5.385\) |
| 30 | \(\sqrt{30} \approx 5.477\) |
| 31 | \(\sqrt{31} \approx 5.568\) |
| 32 | \(\sqrt{32} \approx 5.657\) |
| 33 | \(\sqrt{33} \approx 5.745\) |
| 34 | \(\sqrt{34} \approx 5.831\) |
| 35 | \(\sqrt{35} \approx 5.916\) |
| 36 | \(\sqrt{36} = 6\) |
| 37 | \(\sqrt{37} \approx 6.083\) |
| 38 | \(\sqrt{38} \approx 6.164\) |
| 39 | \(\sqrt{39} \approx 6.245\) |
| 40 | \(\sqrt{40} \approx 6.325\) |
| 41 | \(\sqrt{41} \approx 6.403\) |
| 42 | \(\sqrt{42} \approx 6.481\) |
| 43 | \(\sqrt{43} \approx 6.557\) |
| 44 | \(\sqrt{44} \approx 6.633\) |
| 45 | \(\sqrt{45} \approx 6.708\) |
| 46 | \(\sqrt{46} \approx 6.782\) |
| 47 | \(\sqrt{47} \approx 6.856\) |
| 48 | \(\sqrt{48} \approx 6.928\) |
| 49 | \(\sqrt{49} = 7\) |
| 50 | \(\sqrt{50} \approx 7.071\) |
| 51 | \(\sqrt{51} \approx 7.141\) |
| 52 | \(\sqrt{52} \approx 7.211\) |
| 53 | \(\sqrt{53} \approx 7.280\) |
| 54 | \(\sqrt{54} \approx 7.348\) |
| 55 | \(\sqrt{55} \approx 7.416\) |
| 56 | \(\sqrt{56} \approx 7.483\) |
| 57 | \(\sqrt{57} \approx 7.550\) |
| 58 | \(\sqrt{58} \approx 7.616\) |
| 59 | \(\sqrt{59} \approx 7.681\) |
| 60 | \(\sqrt{60} \approx 7.746\) |
| 61 | \(\sqrt{61} \approx 7.810\) |
| 62 | \(\sqrt{62} \approx 7.874\) |
| 63 | \(\sqrt{63} \approx 7.937\) |
| 64 | \(\sqrt{64} = 8\) |
| 65 | \(\sqrt{65} \approx 8.062\) |
| 66 | \(\sqrt{66} \approx 8.124\) |
| 67 | \(\sqrt{67} \approx 8.185\) |
| 68 | \(\sqrt{68} \approx 8.246\) |
| 69 | \(\sqrt{69} \approx 8.307\) |
| 70 | \(\sqrt{70} \approx 8.367\) |
| 71 | \(\sqrt{71} \approx 8.426\) |
| 72 | \(\sqrt{72} \approx 8.485\) |
| 73 | \(\sqrt{73} \approx 8.544\) |
| 74 | \(\sqrt{74} \approx 8.602\) |
| 75 | \(\sqrt{75} \approx 8.660\) |
| 76 | \(\sqrt{76} \approx 8.718\) |
| 77 | \(\sqrt{77} \approx 8.775\) |
| 78 | \(\sqrt{78} \approx 8.832\) |
| 79 | \(\sqrt{79} \approx 8.888\) |
| 80 | \(\sqrt{80} \approx 8.944\) |
| 81 | \(\sqrt{81} = 9\) |
| 82 | \(\sqrt{82} \approx 9.055\) |
| 83 | \(\sqrt{83} \approx 9.110\) |
| 84 | \(\sqrt{84} \approx 9.165\) |
| 85 | \(\sqrt{85} \approx 9.220\) |
| 86 | \(\sqrt{86} \approx 9.274\) |
| 87 | \(\sqrt{87} \approx 9.327\) |
| 88 | \(\sqrt{88} \approx 9.381\) |
| 89 | \(\sqrt{89} \approx 9.434\) |
| 90 | \(\sqrt{90} \approx 9.487\) |
| 91 | \(\sqrt{91} \approx 9.539\) |
| 92 | \(\sqrt{92} \approx 9.592\) |
| 93 | \(\sqrt{93} \approx 9.644\) |
| 94 | \(\sqrt{94} \approx 9.695\) |
| 95 | \(\sqrt{95} \approx 9.747\) |
| 96 | \(\sqrt{96} \approx 9.798\) |
| 97 | \(\sqrt{97} \approx 9.849\) |
| 98 | \(\sqrt{98} \approx 9.899\) |
| 99 | \(\sqrt{99} \approx 9.950\) |
| 100 | \(\sqrt{100} = 10\) |
Methods to Find Square Roots
Finding the square root of a number can be approached in several ways. Here, we discuss various methods, ranging from basic arithmetic techniques to more advanced algorithms. These methods are useful for different levels of mathematical understanding and applications.
-
Prime Factorization
Prime factorization involves breaking down a number into its prime factors and pairing them to find the square root. This method works best for perfect squares.
- Factorize the number into its prime factors.
- Group the prime factors into pairs.
- Take one factor from each pair and multiply them to get the square root.
-
Long Division Method
The long division method is a systematic approach to find the square root of any number, whether it is a perfect square or not.
- Pair the digits of the number starting from the decimal point.
- Find the largest number whose square is less than or equal to the first pair.
- Subtract the square of this number from the first pair and bring down the next pair of digits.
- Double the divisor and find the next digit of the quotient.
- Continue the process until you have the desired precision.
-
Using Estimation and Approximation
This method involves estimating the square root by finding two close perfect squares and interpolating between them.
- Identify the two closest perfect squares between which the number lies.
- Estimate the square root by averaging the bounds.
- Refine the estimate by considering the distance from the perfect squares.
-
Newton's Method (Newton-Raphson)
Newton's method is an iterative numerical technique to approximate the square root of a number.
- Start with an initial guess for the square root.
- Use the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \) where \( x_n \) is the current guess and \( S \) is the number whose square root is to be found.
- Repeat the iteration until the desired level of accuracy is achieved.
-
Using a Calculator
Modern calculators and computing devices can quickly find the square root of any number using built-in functions.
- Enter the number into the calculator.
- Press the square root function key (\(\sqrt{}\)).
- Read the result displayed on the screen.
Applications of Square Roots
Square roots have numerous applications across various fields. Here are some key areas where square roots are essential:
- Mathematics and Geometry
- Calculating the length of the sides of a right triangle using the Pythagorean theorem: \( c = \sqrt{a^2 + b^2} \).
- Finding the area of a square when the length of one side is known: \( \text{Area} = s^2 \), where \( s = \sqrt{\text{Area}} \).
- Physics
- Determining the root mean square velocity of gas molecules: \( v_{rms} = \sqrt{\frac{3kT}{m}} \), where \( k \) is the Boltzmann constant, \( T \) is temperature, and \( m \) is the mass of a molecule.
- Calculating the distance traveled in uniformly accelerated motion: \( s = \sqrt{2a t} \), where \( a \) is acceleration and \( t \) is time.
- Engineering
- Analyzing stresses and strains in materials to ensure safety and durability of structures.
- Calculating the square root of the sum of the squares of the components in vector analysis: \( |v| = \sqrt{x^2 + y^2 + z^2} \).
- Statistics
- Finding the standard deviation, which is a measure of the amount of variation or dispersion in a set of values: \( \sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}} \).
- Computer Science
- Optimizing algorithms for efficiency, such as using the square root decomposition technique in data structures and algorithms.
- Finance
- Calculating the volatility of stock prices using the standard deviation formula in stock market analysis.
- Astronomy
- Determining the luminosity of stars based on their apparent brightness and distance: \( L = \sqrt{4 \pi d^2 F} \), where \( L \) is luminosity, \( d \) is distance, and \( F \) is flux.
Square Roots in Real Life
Square roots are more than just a mathematical concept; they have a variety of practical applications in everyday life. Here are some of the key areas where square roots are used:
- Architecture and Engineering: Square roots are crucial in calculating areas and dimensions, which are essential for designing buildings and other structures. For instance, determining the length of the diagonal of a square or rectangular plot requires the use of the Pythagorean theorem, which involves square roots.
- Physics: Square roots are often used in physics to solve equations related to waves, such as sound and light waves. The intensity of these waves is proportional to the square of the amplitude, and thus calculating the root is necessary for understanding their properties.
- Finance: In finance, square roots are used to calculate standard deviation, which is a measure of the amount of variation or dispersion of a set of values. This is critical for assessing the risk associated with investments.
- Medicine: In medical research, square roots are used in various statistical calculations, including the analysis of variance (ANOVA) and other tests that help in understanding the data distribution and variability.
- Agriculture: Farmers use square roots to calculate the proper spacing for planting crops. For example, if a farmer wants to plant crops in a square area, they might need to determine the length of each side of the square root of the total area.
- Computer Science: Algorithms often involve square roots, especially in graphics programming and encryption. For example, calculating the distance between two points in a digital image involves square roots.
Understanding and using square roots can simplify many practical problems and help in making precise calculations in various fields. They are fundamental tools in both scientific research and everyday problem-solving.

Square Roots and Geometry
Square roots play a fundamental role in various aspects of geometry, enabling us to calculate distances, areas, and dimensions with precision. Here are some key applications of square roots in geometry:
1. Calculating Distances
The distance formula in coordinate geometry, used to find the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\), involves square roots:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
This formula is derived from the Pythagorean theorem and is crucial for determining the straight-line distance between points in a plane.
2. Pythagorean Theorem
The Pythagorean theorem states that in a right-angled triangle, the square of the hypotenuse (\(c\)) is equal to the sum of the squares of the other two sides (\(a\) and \(b\)):
\[
c = \sqrt{a^2 + b^2}
\]
This theorem is foundational in geometry, allowing us to solve for any side of a right-angled triangle given the other two.
3. Finding Areas
Square roots are essential when dealing with areas of geometric shapes:
- Square: The side length (\(s\)) of a square can be found if the area (\(A\)) is known:
\[
s = \sqrt{A}
\] - Circle: The radius (\(r\)) of a circle can be determined from its area (\(A = \pi r^2\)):
\[
r = \sqrt{\frac{A}{\pi}}
\]
4. Diagonals of Polygons
The length of the diagonal (\(d\)) of a rectangle with sides \(a\) and \(b\) is calculated using the Pythagorean theorem:
\[
d = \sqrt{a^2 + b^2}
\]
For a square with side length \(s\), the diagonal is:
\[
d = s\sqrt{2}
\]
5. Conic Sections
Square roots are involved in the equations of conic sections (ellipses, hyperbolas) where they help in defining distances and dimensions.
6. Transformations
In transformations, especially scaling, square roots help determine the new dimensions of geometric shapes when scaling up or down.
Understanding and applying square roots in geometry allows for accurate calculations and a deeper comprehension of spatial relationships and properties.
Common Square Roots
Square roots are fundamental in mathematics, and understanding the square roots of common numbers can be very useful. Below is a table of square roots for numbers from 1 to 100:
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 2 | \(\sqrt{2} \approx 1.414\) |
| 3 | \(\sqrt{3} \approx 1.732\) |
| 4 | \(\sqrt{4} = 2\) |
| 5 | \(\sqrt{5} \approx 2.236\) |
| 6 | \(\sqrt{6} \approx 2.449\) |
| 7 | \(\sqrt{7} \approx 2.646\) |
| 8 | \(\sqrt{8} \approx 2.828\) |
| 9 | \(\sqrt{9} = 3\) |
| 10 | \(\sqrt{10} \approx 3.162\) |
Here are some of the most commonly known square roots:
- \(\sqrt{16} = 4\) - 16 is a perfect square, and its square root is 4.
- \(\sqrt{25} = 5\) - 25 is a perfect square, and its square root is 5.
- \(\sqrt{36} = 6\) - 36 is a perfect square, and its square root is 6.
- \(\sqrt{49} = 7\) - 49 is a perfect square, and its square root is 7.
- \(\sqrt{64} = 8\) - 64 is a perfect square, and its square root is 8.
- \(\sqrt{81} = 9\) - 81 is a perfect square, and its square root is 9.
- \(\sqrt{100} = 10\) - 100 is a perfect square, and its square root is 10.
Understanding these common square roots can help in various mathematical calculations and problem-solving scenarios.
Square Roots and Algebra
Square roots play a significant role in algebra, appearing in various equations and expressions. Understanding how to manipulate and solve square root equations is crucial for mastering algebra. Here are some key concepts and examples:
Basic Concepts
- Definition: The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\).
- Notation: The square root of \(x\) is denoted as \(\sqrt{x}\).
- Properties:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
Solving Square Root Equations
To solve equations involving square roots, follow these steps:
- Isolate the square root expression.
- Square both sides of the equation to eliminate the square root.
- Solve the resulting equation.
- Check all solutions in the original equation to avoid extraneous solutions.
Example:
Solve \(\sqrt{x + 3} = 5\).
- Isolate the square root: \(\sqrt{x + 3} = 5\).
- Square both sides: \((\sqrt{x + 3})^2 = 5^2\).
- Simplify: \(x + 3 = 25\).
- Solve for \(x\): \(x = 22\).
- Check the solution: \(\sqrt{22 + 3} = \sqrt{25} = 5\). The solution \(x = 22\) is correct.
Quadratic Equations
Square roots are often used to solve quadratic equations of the form \(ax^2 + bx + c = 0\). The quadratic formula is:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Example:
Solve \(2x^2 - 4x - 6 = 0\) using the quadratic formula.
- Identify \(a = 2\), \(b = -4\), and \(c = -6\).
- Calculate the discriminant: \(b^2 - 4ac = (-4)^2 - 4(2)(-6) = 16 + 48 = 64\).
- Apply the quadratic formula: \[ x = \frac{-(-4) \pm \sqrt{64}}{2(2)} = \frac{4 \pm 8}{4} \]
- Simplify: \[ x = \frac{4 + 8}{4} = 3 \quad \text{and} \quad x = \frac{4 - 8}{4} = -1 \]
- The solutions are \(x = 3\) and \(x = -1\).
Rationalizing the Denominator
When an expression has a square root in the denominator, it is often useful to rationalize the denominator.
Example:
Simplify \(\frac{5}{\sqrt{2}}\).
- Multiply the numerator and denominator by \(\sqrt{2}\): \(\frac{5}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{5\sqrt{2}}{2}\).
- The simplified form is \(\frac{5\sqrt{2}}{2}\).
By understanding and applying these principles, you can effectively handle square roots in various algebraic contexts.
Historical Significance of Square Roots
The concept of square roots has a rich history that spans several millennia and civilizations. Here, we explore the historical significance of square roots and their development over time.
Ancient Civilizations
- Babylonians: The Babylonians, around 2000 BCE, were among the first to use approximations for square roots. They used a method similar to the modern-day algorithm for finding square roots.
- Egyptians: The Rhind Mathematical Papyrus (circa 1650 BCE) shows that ancient Egyptians had an understanding of square roots and used them in their calculations.
- Greeks: Greek mathematicians like Pythagoras (circa 500 BCE) and Euclid (circa 300 BCE) made significant contributions to the understanding of square roots. Euclid's Elements includes geometric methods for finding square roots.
Middle Ages
- Islamic Scholars: Islamic mathematicians made significant advances in algebra and the study of square roots. Al-Khwarizmi (circa 800 CE) included methods for extracting square roots in his works, which influenced later European mathematics.
- Indian Mathematicians: Aryabhata (476-550 CE) and Brahmagupta (598-668 CE) made notable contributions to the methods of calculating square roots. Brahmagupta's formula for the area of a cyclic quadrilateral uses square roots.
Renaissance and Enlightenment
- Europe: During the Renaissance, European mathematicians such as Leonardo of Pisa (Fibonacci) and later, René Descartes, continued to develop and refine methods for working with square roots. The development of algebraic notation by Descartes made it easier to express and manipulate square roots algebraically.
Modern Era
- Development of Calculators and Computers: The invention of mechanical calculators in the 17th century and electronic computers in the 20th century revolutionized the way square roots are computed, making it possible to find square roots of large numbers quickly and accurately.
- Educational Importance: Today, square roots are a fundamental concept taught in mathematics education worldwide. They are essential for understanding higher-level mathematics, physics, engineering, and various applied sciences.
Significance in Mathematics
Square roots are not only crucial in solving quadratic equations but also play a significant role in various branches of mathematics, including:
- Geometry: Used in the Pythagorean theorem to determine the length of the sides of a right triangle.
- Algebra: Essential in simplifying expressions and solving equations.
- Calculus: Appear in derivative and integral calculations involving square root functions.
- Number Theory: Used in the study of perfect squares, irrational numbers, and modular arithmetic.
Throughout history, the development and understanding of square roots have been pivotal in advancing mathematical thought and its applications. From ancient civilizations to modern technology, square roots continue to be a vital component of mathematics.

Tips for Learning Square Roots
Learning square roots can be challenging, but with the right strategies and practice, it can become much easier. Here are some tips to help you master square roots:
Understand the Concept
Before diving into calculations, make sure you understand what a square root is. The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\). For example, \(\sqrt{9} = 3\) because \(3^2 = 9\).
Memorize Perfect Squares
Knowing the perfect squares from 1 to 100 can greatly speed up your ability to recognize square roots. Here are the perfect squares up to 100:
- \(1^2 = 1\)
- \(2^2 = 4\)
- \(3^2 = 9\)
- \(4^2 = 16\)
- \(5^2 = 25\)
- \(6^2 = 36\)
- \(7^2 = 49\)
- \(8^2 = 64\)
- \(9^2 = 81\)
- \(10^2 = 100\)
Use Estimation
When dealing with non-perfect squares, use estimation to find approximate square roots. For example, to find \(\sqrt{50}\), note that it lies between \(\sqrt{49} = 7\) and \(\sqrt{64} = 8\). Thus, \(\sqrt{50} \approx 7.1\).
Learn the Prime Factorization Method
Use prime factorization to simplify square roots. For instance, to find \(\sqrt{72}\), write 72 as \(2^3 \cdot 3^2\). Then, \(\sqrt{72} = \sqrt{2^3 \cdot 3^2} = \sqrt{2^2 \cdot 2 \cdot 3^2} = 6\sqrt{2}\).
Practice with Worksheets and Online Tools
Regular practice is key. Use worksheets, online quizzes, and apps to practice calculating square roots. Consistent practice helps reinforce your understanding and improve your speed.
Visualize with Geometry
Use geometric representations to understand square roots. For example, the side length of a square with an area of 16 units is \(\sqrt{16} = 4\) units. Visualizing square roots as side lengths of squares can aid in comprehension.
Understand the Properties of Square Roots
Learn and apply the properties of square roots, such as:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
Use the Square Root Algorithm
For more complex square roots, use the long division-like square root algorithm to find precise values. This method involves grouping digits, finding the largest possible square, and subtracting iteratively.
Apply Square Roots in Real Life
Connecting square roots to real-life applications can make learning more interesting. For example, use square roots in measuring distances, areas, and understanding scientific formulas.
By following these tips and practicing regularly, you can develop a strong understanding of square roots and improve your mathematical skills.
Practice Problems
Practicing square root problems is essential to solidify your understanding and improve your skills. Below are a variety of practice problems ranging from basic to advanced levels. Work through each problem step-by-step and check your answers to ensure accuracy.
Basic Problems
- Find the square root of 16.
- Calculate \(\sqrt{25}\).
- What is \(\sqrt{81}\)?
- Determine the square root of 64.
- Simplify \(\sqrt{49}\).
Intermediate Problems
- Simplify \(\sqrt{50}\).
- Find the square root of 72 using prime factorization.
- Calculate \(\sqrt{121}\).
- What is \(\sqrt{225}\)?
- Determine the value of \(\sqrt{144}\).
Advanced Problems
- Solve for \(x\) if \(\sqrt{x} = 12\).
- If \(\sqrt{2x + 3} = 5\), what is the value of \(x\)?
- Simplify \(\sqrt{75}\).
- Find the value of \(\sqrt{256}\).
- If \(\sqrt{x^2 + 6x + 9} = 7\), solve for \(x\).
Application Problems
- The area of a square is 49 square units. What is the length of one side?
- A right triangle has legs of lengths 3 and 4. What is the length of the hypotenuse?
- The distance between two points on a coordinate plane is given by \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\). Find the distance between the points \((1, 2)\) and \((4, 6)\).
- A square garden has an area of 100 square feet. What is the length of each side of the garden?
- If the diagonal of a square is 10 units, what is the length of one side of the square?
Challenge Problems
- Simplify the expression \(\sqrt{18} + \sqrt{8}\).
- Rationalize the denominator: \(\frac{5}{\sqrt{3}}\).
- If \(\sqrt{x + 2} + \sqrt{x - 2} = 4\), solve for \(x\).
- Find the square root of \(0.0004\).
- Solve the equation \(\sqrt{3x + 4} - \sqrt{x - 1} = 2\).
By working through these problems, you will gain a deeper understanding of square roots and improve your problem-solving skills. Be sure to review your work and understand each step to ensure you have mastered the concepts.
FAQs about Square Roots
Below are some frequently asked questions about square roots, along with detailed explanations to help you better understand this important mathematical concept.
What is a square root?
A square root of a number \(x\) is a value \(y\) such that \(y^2 = x\). For example, the square root of 25 is 5 because \(5^2 = 25\).
How do you find the square root of a number?
To find the square root of a number, you can use several methods:
- For perfect squares (e.g., 1, 4, 9, 16), the square root is an integer.
- For non-perfect squares, use estimation, prime factorization, or a calculator for more accuracy.
What are perfect squares?
Perfect squares are numbers that are the product of an integer multiplied by itself. Examples include \(1, 4, 9, 16, 25, 36, 49, 64, 81,\) and \(100\).
Can square roots be negative?
The principal square root of a number is always non-negative. However, every positive number has two square roots: one positive and one negative. For example, the square roots of 9 are 3 and -3 because both \(3^2 = 9\) and \((-3)^2 = 9\).
What is an irrational number?
An irrational number is a number that cannot be expressed as a simple fraction. The square roots of non-perfect squares are often irrational. For example, \(\sqrt{2}\) is an irrational number.
How do you simplify square roots?
To simplify square roots, factor the number into its prime factors and then simplify:
- Find the prime factorization of the number.
- Group the factors into pairs.
- Move each pair of factors out of the square root as a single factor.
Example: Simplify \(\sqrt{72}\).
- Prime factorization of 72 is \(2^3 \cdot 3^2\).
- Group the factors: \(\sqrt{2^3 \cdot 3^2} = \sqrt{2^2 \cdot 2 \cdot 3^2}\).
- Simplify: \(\sqrt{2^2} \cdot \sqrt{3^2} \cdot \sqrt{2} = 2 \cdot 3 \cdot \sqrt{2} = 6\sqrt{2}\).
What is the difference between \(\sqrt{x}\) and \(x^{1/2}\)?
There is no difference; \(\sqrt{x}\) and \(x^{1/2}\) are two notations for the same mathematical operation. Both represent the square root of \(x\).
What are the applications of square roots?
Square roots have numerous applications in various fields, including:
- Geometry: Calculating distances and areas.
- Algebra: Solving quadratic equations.
- Physics: Describing physical laws and properties.
- Engineering: Designing and analyzing systems and structures.
- Statistics: Calculating standard deviations and variances.
How do calculators find square roots?
Calculators use efficient algorithms like the Newton-Raphson method to compute square roots quickly and accurately. These methods involve iterative approximations to reach a precise value.
What is the square root of 0?
The square root of 0 is 0 because \(0^2 = 0\).
By understanding these FAQs, you can deepen your knowledge of square roots and their applications in various mathematical contexts.
Conclusion
Understanding square roots is a fundamental aspect of mathematics that has applications in various fields including geometry, algebra, physics, and engineering. From the historical significance of square roots to their practical applications, we have explored the many facets of this important concept.
By memorizing perfect squares, practicing estimation, and using prime factorization, one can efficiently calculate square roots. Additionally, the use of modern technology such as calculators and computer algorithms has made it easier to compute square roots with high precision.
Square roots also play a crucial role in solving real-world problems, from calculating distances and areas to understanding scientific principles. The development and use of square roots throughout history demonstrate their enduring importance in advancing mathematical thought and application.
As you continue to explore square roots, remember to practice regularly and apply the concepts to various problems. Utilize the methods and tips discussed, such as simplifying square roots, using visual aids, and connecting square roots to real-life scenarios, to strengthen your understanding and proficiency.
In summary, mastering square roots not only enhances your mathematical skills but also opens up a deeper appreciation for the elegance and utility of mathematics in our daily lives. Keep practicing and exploring, and you will continue to grow in your mathematical journey.
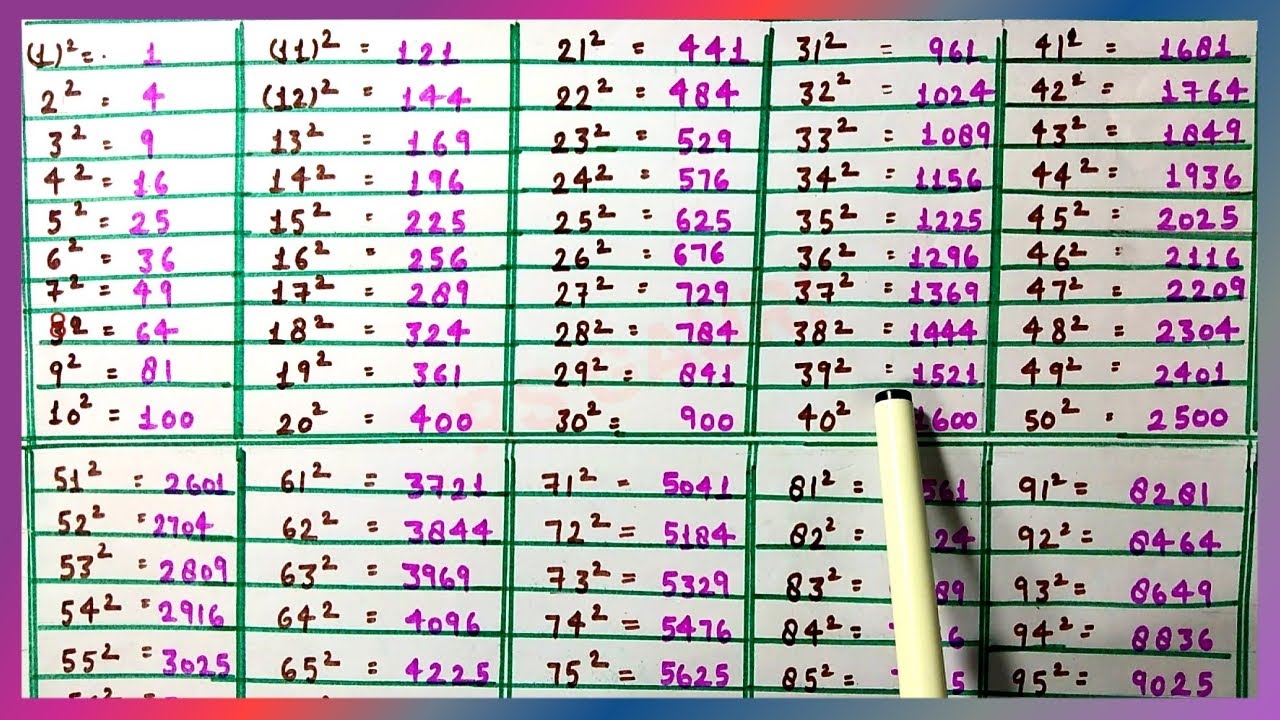
Toán Lớp 8 | Bình Phương và Căn Bậc Hai | Bình Phương từ 1 đến 100
READ MORE:
Xem video về bảng căn bậc hai từ 1 đến 100 và bảng bình phương từ 1 đến 100. Tìm hiểu cách tính căn bậc hai của các số từ 1 đến 100 một cách dễ dàng.
Bảng căn bậc hai từ 1 đến 100. Bảng bình phương và căn bậc hai từ 1 đến 100 toán học. (√1, √2, √3...√100)