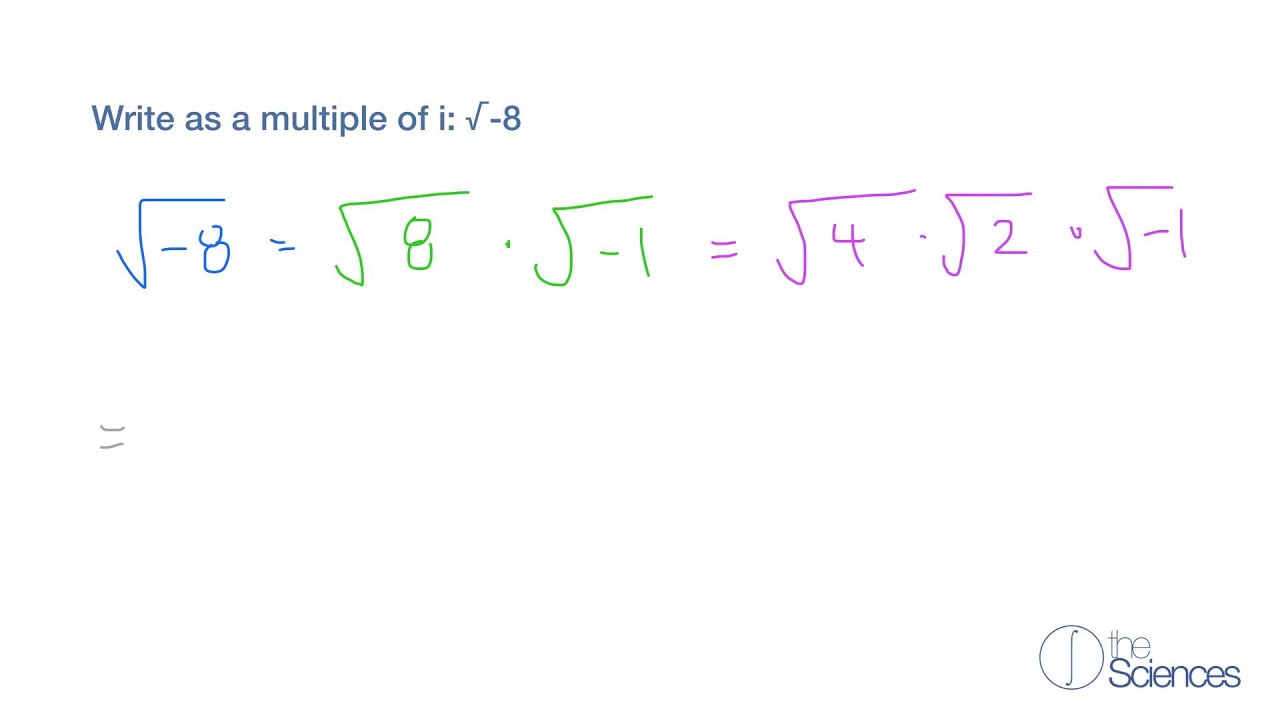Topic negative square root of 1: The negative square root of 1, represented as √-1, is a fundamental concept in mathematics, especially within the realm of complex numbers. This introduction will explore its significance and applications, providing a comprehensive overview for readers looking to deepen their understanding of imaginary numbers and their properties.
Table of Content
The Square Root of Negative One
The square root of negative one is a fundamental concept in mathematics, represented by the imaginary unit i. This concept extends beyond real numbers into the complex number system.
Definition
In mathematics, the imaginary unit i is defined as the square root of -1:
\[
i = \sqrt{-1}
\]
This means that:
\[
i^2 = -1
\]
Finding the Square Root of Negative Numbers
To find the square root of a negative number, we use the property of the imaginary unit. For any positive real number x, the square root of -x can be expressed as:
\[
\sqrt{-x} = i\sqrt{x}
\]
This is because:
\[
(i\sqrt{x})^2 = i^2 \cdot (\sqrt{x})^2 = -1 \cdot x = -x
\]
Examples
- Example 1: \[ \sqrt{-25} = \sqrt{(-1) \cdot 25} = \sqrt{-1} \cdot \sqrt{25} = i \cdot 5 = 5i \]
- Example 2: \[ \sqrt{-9} = \sqrt{(-1) \cdot 9} = \sqrt{-1} \cdot \sqrt{9} = i \cdot 3 = 3i \]
Complex Numbers
Complex numbers are numbers that have both a real part and an imaginary part, typically written in the form a + bi where a and b are real numbers, and i is the imaginary unit.
Examples of complex numbers include:
- 3 + 4i
- 5 - 2i
- -7 + 6i
Applications
Imaginary and complex numbers are used in various fields including engineering, physics, and signal processing. For instance, in electrical engineering, complex numbers are used to analyze alternating current (AC) circuits.
Conclusion
Understanding the square root of negative one and its applications in complex numbers provides a deeper insight into mathematical concepts that extend beyond real numbers. The imaginary unit i plays a crucial role in these advanced topics.

READ MORE:
Introduction
The concept of the negative square root of 1 leads us to the realm of complex numbers. By definition, the square root of -1 is denoted as the imaginary unit \(i\), where \(i^2 = -1\). Understanding this fundamental concept allows us to explore a range of mathematical and real-world applications, from solving equations with no real solutions to complex signal processing in engineering.
Complex Numbers and Imaginary Units
Complex numbers extend the concept of one-dimensional real numbers to the two-dimensional complex plane by using the imaginary unit, \(i\), where \(i\) is defined as the square root of -1 (\(\sqrt{-1} = i\)). This allows for the square roots of negative numbers to be represented in terms of \(i\).
Here are some important points about complex numbers and imaginary units:
- The imaginary unit \(i\) is defined by the property \(i^2 = -1\).
- Any complex number can be written as \(a + bi\), where \(a\) and \(b\) are real numbers.
- The number \(a\) is called the real part, and \(b\) is the imaginary part of the complex number.
- To find the square root of a negative number, such as -x, we use the property \(\sqrt{-x} = i\sqrt{x}\).
For example, the square root of -9 can be calculated as follows:
\[
\sqrt{-9} = \sqrt{9 \times -1} = \sqrt{9} \times \sqrt{-1} = 3i
\]
This shows that the square root of -9 is \(3i\). Similarly, the square root of any negative number involves the imaginary unit \(i\).
Using imaginary units allows us to solve equations that have no real solutions. For instance, the equation \(x^2 + 1 = 0\) has solutions \(x = \pm i\), which are complex numbers.
Imaginary and complex numbers are crucial in many fields of science and engineering, including signal processing, quantum mechanics, and electrical engineering.
Principal Square Root
The principal square root of a number is its non-negative square root. For negative numbers, this concept extends to the realm of complex numbers. The principal square root of -1 is denoted by the imaginary unit "i", where \( i^2 = -1 \).
Mathematically, to find the principal square root of any negative number \(-x\), we can express it as follows:
- \(\sqrt{-x} = \sqrt{(-1) \cdot x}\)
- Using the property of square roots, we can split this into: \(\sqrt{-x} = \sqrt{-1} \cdot \sqrt{x}\)
- Since \(\sqrt{-1} = i\), it simplifies to: \(\sqrt{-x} = i \cdot \sqrt{x}\)
Let's look at a few examples to understand this better:
| Example | Calculation | Result |
|---|---|---|
| \(\sqrt{-4}\) | \(\sqrt{-4} = \sqrt{4 \cdot -1} = \sqrt{4} \cdot \sqrt{-1} = 2i\) | 2i |
| \(\sqrt{-25}\) | \(\sqrt{-25} = \sqrt{25 \cdot -1} = \sqrt{25} \cdot \sqrt{-1} = 5i\) | 5i |
| \(\sqrt{-81}\) | \(\sqrt{-81} = \sqrt{81 \cdot -1} = \sqrt{81} \cdot \sqrt{-1} = 9i\) | 9i |
In general, the principal square root of a negative number \(-x\) is \(i \cdot \sqrt{x}\). This extension to complex numbers allows us to handle square roots of negative values, which are not possible within the realm of real numbers alone.
Properties and Examples
Understanding the properties and examples of the square root of negative numbers is crucial for working with complex numbers. Here are some key properties and examples to help illustrate these concepts:
- When dealing with negative numbers under a square root, the result is an imaginary number. For example, the square root of -1 is denoted as i, where \(i^2 = -1\).
- The property \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) does not hold if both \(a\) and \(b\) are negative. Instead, we use imaginary units to represent the results correctly.
- For any negative number \( -a \), its square root can be written as \( \sqrt{-a} = \sqrt{a} \cdot i \).
Here are some examples demonstrating these properties:
| Expression | Result |
|---|---|
| \(i^2\) | \(-1\) |
| \(\sqrt{-4}\) | \(2i\) |
| \((5i)^2\) | \(-25\) |
| \(\sqrt{-(16)}\) | \(4i\) |
| \((3i)^2\) | \(-9\) |
These examples demonstrate the unique nature of imaginary numbers and how they interact with negative values under square roots. Understanding these properties is essential for solving complex equations and applying these concepts in various fields such as engineering and physics.

Applications of Imaginary Numbers
Imaginary numbers have a wide range of applications in various fields, including engineering, physics, and applied mathematics. They are particularly useful in dealing with problems that involve periodic functions and waveforms.
-
Electrical Engineering:
In electrical engineering, imaginary numbers are used to analyze and design circuits. For instance, in alternating current (AC) circuit analysis, complex numbers simplify the calculation of impedance, voltage, and current. The impedance of an AC circuit is represented as a complex number \(Z = R + jX\), where \(R\) is resistance and \(X\) is reactance.
-
Signal Processing:
Imaginary numbers play a crucial role in signal processing. They are used in the representation and manipulation of signals, particularly in the Fourier transform, which converts signals between time and frequency domains. The Fourier transform uses complex numbers to handle sinusoidal components of signals.
-
Control Theory:
In control theory, complex numbers help in analyzing the stability of systems. The roots of the characteristic equation of a system, which are generally complex numbers, determine the system's stability. If the real parts of these roots are negative, the system is stable.
-
Quantum Mechanics:
Quantum mechanics relies heavily on complex numbers. The state of a quantum system is described by a complex-valued wave function, and the probabilities of different outcomes are calculated using these complex functions.
-
Vibrations and Waves:
In the study of vibrations and wave phenomena, complex numbers simplify the mathematics involved. For example, the solution to the differential equations describing wave motion often involves complex exponentials.
Overall, imaginary numbers provide a powerful tool for simplifying and solving problems in various scientific and engineering disciplines, enabling precise and efficient analysis of complex systems.
Hướng dẫn về căn bậc hai của số âm một và các thuật toán liên quan.
The Square Root Of Negative One | Căn bậc hai của Số Âm Một
READ MORE:
Hướng dẫn cách đơn giản hóa các căn bậc hai âm và các phép toán liên quan.
Đơn giản hóa các căn bậc hai âm | Simplifying negative radicals