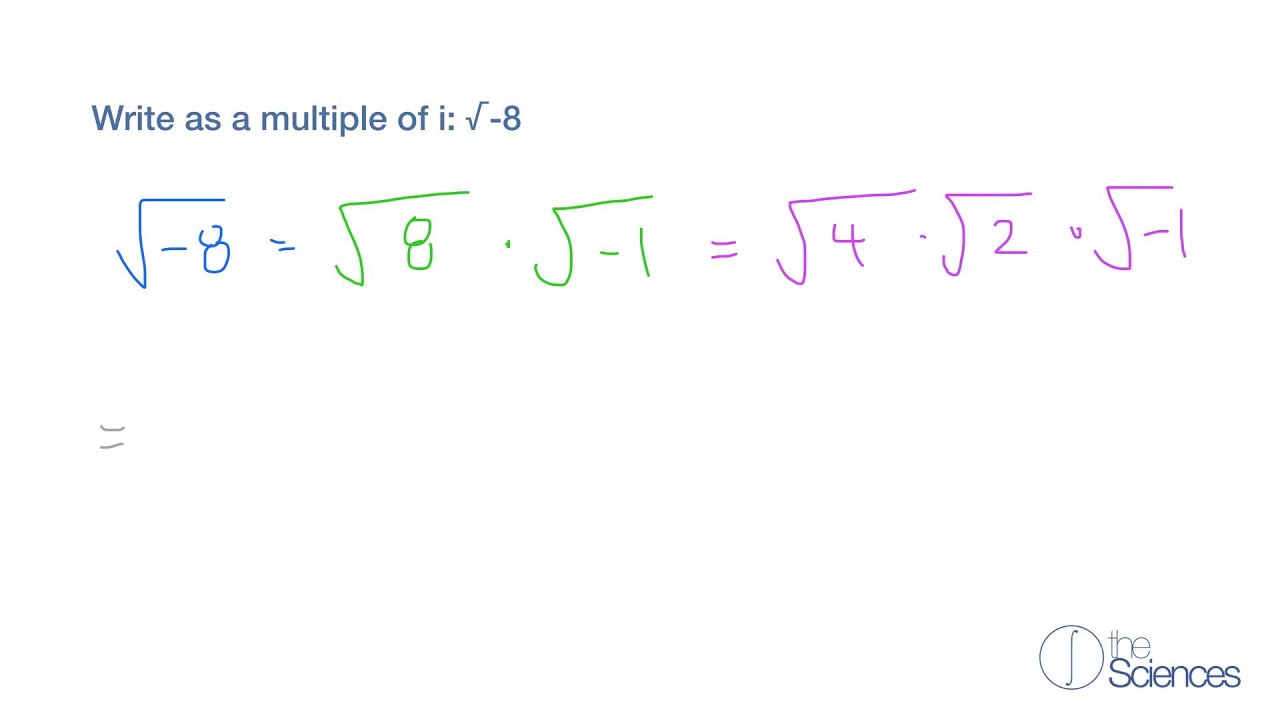Topic square root of negative 7: The square root of negative 7 introduces us to the fascinating world of imaginary numbers. Understanding how to handle these complex calculations is essential for advanced mathematics, particularly in fields like engineering and physics. This guide will help you navigate the concept of the square root of negative 7 and its applications.
Table of Content
- Understanding the Square Root of Negative 7
- Introduction to Square Roots
- Imaginary Numbers and Square Roots
- Calculation Methods
- Practical Applications
- Examples and Exercises
- Related Concepts
- YOUTUBE: Hướng dẫn cách tìm căn bậc hai của số âm, rất phù hợp cho những ai muốn hiểu rõ về số phức và ứng dụng của chúng.
Understanding the Square Root of Negative 7
The square root of a negative number is a concept that extends beyond the realm of real numbers and into the domain of complex numbers. This concept is essential in various fields of mathematics, including algebra and calculus.
Imaginary Numbers
An imaginary number is defined as a number that gives a negative result when squared. The most fundamental imaginary number is \(i\), which is the square root of -1:
$$i = \sqrt{-1}$$
Using this, we can express the square root of any negative number. For example, the square root of -7 can be written as:
$$\sqrt{-7} = \sqrt{7} \cdot i$$
Properties of Imaginary Numbers
Imaginary numbers follow specific arithmetic rules similar to real numbers but include the crucial property:
$$i^2 = -1$$
Calculating the Square Root of -7
To calculate the square root of -7, we can follow these steps:
- Identify the positive counterpart: \(7\)
- Calculate the square root of the positive number: \(\sqrt{7}\)
- Multiply the result by \(i\):
Thus, the result is:
$$\sqrt{-7} = \sqrt{7} \cdot i \approx 2.6457513110645906i$$
Applications
Understanding imaginary numbers and their properties is crucial in various applications:
- Electrical Engineering: Used in analyzing AC circuits.
- Signal Processing: Used in Fourier transforms and related calculations.
- Quantum Physics: Imaginary numbers are part of the Schrödinger equation.
Conclusion
The concept of imaginary numbers, including the square root of negative numbers, extends our ability to solve equations and understand phenomena that cannot be explained by real numbers alone. The square root of -7, expressed as \(2.6457513110645906i\), demonstrates the elegant complexity of mathematical concepts beyond the real number line.

READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing the value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3, as \(3^2 = 9\). Square roots can be both positive and negative, but the principal square root is always the non-negative value.
For positive numbers, calculating the square root is straightforward. However, for negative numbers, the concept involves imaginary numbers. The square root of a negative number, such as \(-7\), is expressed using the imaginary unit \(i\), where \(i = \sqrt{-1}\). Thus, the square root of \(-7\) is represented as \(\sqrt{-7} = \sqrt{7}i\).
There are several methods to calculate square roots, such as the Babylonian Method (or Hero's Method), which is an iterative approximation technique. This method starts with a guess and repeatedly averages it with the quotient of the original number and the guess until the result stabilizes.
Understanding square roots is crucial as they are used in various mathematical applications, from solving quadratic equations to complex number calculations. Square roots also play a significant role in geometry, physics, and engineering.
Below is a step-by-step breakdown of how to approximate the square root of a number using the Babylonian Method:
- Guess a convenient value for the square root.
- Divide the number by your guess.
- Take the average of your guess and the quotient to get a new guess.
- Repeat the process until the guesses stabilize.
For example, to approximate \(\sqrt{7}\):
- Start with a guess, say 3.
- Divide 7 by 3 to get approximately 2.33.
- Average 3 and 2.33 to get a new guess, 2.67.
- Repeat with the new guess: 7 / 2.67 ≈ 2.62, average 2.67 and 2.62 to get 2.645.
Repeating this process will yield an increasingly accurate approximation of \(\sqrt{7}\).
By understanding and applying these principles, you can effectively handle square roots in various mathematical contexts.
Imaginary Numbers and Square Roots
Imaginary numbers arise when we take the square root of a negative number. This concept extends our number system to include values that are not real, but still useful in many mathematical applications. The fundamental imaginary unit is denoted as \(i\), where \(i = \sqrt{-1}\). This allows us to express the square root of any negative number as a multiple of \(i\).
For instance, the square root of -7 can be written as:
\[\sqrt{-7} = \sqrt{7} \cdot \sqrt{-1} = \sqrt{7} \cdot i\]
Thus, the square root of -7 is expressed as \(\sqrt{7}i\).
Imaginary numbers are part of a larger system called complex numbers, which combine real and imaginary parts. A complex number is written as \(a + bi\), where \(a\) and \(b\) are real numbers, and \(i\) is the imaginary unit.
Here is a step-by-step process to understand this better:
- Identify the negative number: For example, -7.
- Express the negative number as a product: Rewrite -7 as 7 multiplied by -1.
- Separate the square roots: Apply the property of square roots to get \(\sqrt{7} \cdot \sqrt{-1}\).
- Substitute the imaginary unit: Recognize that \(\sqrt{-1} = i\), so the expression becomes \(\sqrt{7}i\).
Understanding imaginary numbers and their square roots is crucial in fields such as engineering, physics, and computer science, where they help solve equations that do not have real solutions.
Calculation Methods
Calculating the square root of negative numbers involves understanding the concept of imaginary numbers. Here's a detailed, step-by-step method to find the square root of negative numbers, specifically focusing on -7:
- Identify the negative number whose square root you need to find. For example, -7.
- Recognize that the square root of a negative number is not a real number, but an imaginary number. The imaginary unit \( i \) is defined as \( i = \sqrt{-1} \).
- Rewrite the square root of the negative number using the imaginary unit. For \( \sqrt{-7} \), this can be expressed as \( \sqrt{7} \cdot \sqrt{-1} \), which simplifies to \( \sqrt{7} \cdot i \).
- Therefore, the square root of -7 is \( i\sqrt{7} \).
This method is consistent for any negative number. Here’s a summary table for better understanding:
| Negative Number | Square Root |
|---|---|
| -1 | \( i \) |
| -4 | \( 2i \) |
| -9 | \( 3i \) |
| -16 | \( 4i \) |
| -25 | \( 5i \) |
Understanding this concept allows you to handle the square roots of all negative numbers by converting them into their imaginary form using the imaginary unit \( i \).
Practical Applications
The concept of the square root of negative numbers, including the square root of negative 7, plays a significant role in various fields such as engineering, physics, and computer science. These square roots are known as imaginary numbers, denoted with the imaginary unit i, where i = √-1. Let's explore some practical applications of these concepts.
- Electrical Engineering:
Imaginary numbers are essential in the analysis of electrical circuits, particularly in alternating current (AC) circuit analysis. They help in representing the phase difference between the voltage and the current.
- Signal Processing:
In signal processing, imaginary numbers are used in the Fourier transform, which converts a time-domain signal into its frequency-domain components. This is crucial for understanding and manipulating signals.
- Quantum Mechanics:
Quantum mechanics heavily relies on complex numbers (comprising real and imaginary parts) to describe the state of a quantum system. The Schrödinger equation, which predicts the behavior of particles, utilizes imaginary numbers.
- Control Systems:
In control systems engineering, imaginary numbers are used in the analysis of system stability and response. They help in designing systems that can maintain desired performance under various conditions.
- Fluid Dynamics:
Complex analysis, involving imaginary numbers, is used in fluid dynamics to solve problems related to fluid flow. This includes potential flow theory, which models the flow of incompressible fluids.
Examples and Exercises
Understanding the square root of negative numbers, such as the square root of negative 7, involves grasping the concept of imaginary numbers. Below are some examples and exercises to help reinforce this understanding.
- Example 1: Calculate the square root of -7.
- Example 2: Simplify the expression \( √(-9) + √(-16) \).
- Exercise 1: Solve for x in the equation \( x^2 + 7 = 0 \).
- Exercise 2: Express the product of √(-5) and √(-2) in simplest form.
- Example 3: Verify if \( x = i√7 \) is a solution to the equation \( x^2 + 7 = 0 \).
The square root of -7 can be expressed as √(-7) = √(7) * √(-1). Since √(-1) is represented by the imaginary unit \( i \), the result is: √(-7) = \( i√7 \).
First, express each square root in terms of \( i \):
√(-9) = 3i and √(-16) = 4i.
Then add the imaginary components: 3i + 4i = 7i.
First, isolate \( x^2 \) by subtracting 7 from both sides: \( x^2 = -7 \).
Taking the square root of both sides gives \( x = ± i√7 \).
First, use the property of square roots: √(-5) * √(-2) = √(10) * √(-1) * √(-1) = √10 * -1 = -√10.
Substitute \( x = i√7 \) into the equation:
\((i√7)^2 + 7 = -7 + 7 = 0\).
This confirms that \( x = i√7 \) is indeed a solution.
Related Concepts
Understanding the square root of negative numbers opens the door to several advanced mathematical concepts. Here are a few related topics that further explore the world of complex and imaginary numbers:
-
Complex Numbers
Complex numbers consist of a real part and an imaginary part, expressed as \( a + bi \), where \( a \) and \( b \) are real numbers, and \( i \) is the imaginary unit. Complex numbers are fundamental in various fields, including electrical engineering, quantum physics, and applied mathematics.
-
Arithmetic of Complex Numbers
Operations with complex numbers include addition, subtraction, multiplication, and division. For example:
- \((3 + 4i) + (2 - 3i) = 5 + i\)
- \((3 + 4i) - (2 - 3i) = 1 + 7i\)
- \((3 + 4i) \cdot (2 - 3i) = 6 - 9i + 8i - 12i^2 = 18 + i\) (since \(i^2 = -1\))
- \(\frac{3 + 4i}{2 - 3i} = \frac{(3 + 4i)(2 + 3i)}{(2 - 3i)(2 + 3i)} = \frac{6 + 9i + 8i + 12}{4 + 9} = \frac{18 + 17i}{13}\)
-
Polar Form of Complex Numbers
Complex numbers can also be represented in polar form as \( r(\cos \theta + i \sin \theta) \), where \( r \) is the modulus and \( \theta \) is the argument of the complex number.
-
Arithmetic of Complex Numbers
-
Euler's Formula
Euler's formula, \( e^{i\theta} = \cos \theta + i \sin \theta \), connects complex exponentiation with trigonometric functions. This formula is crucial for understanding the behavior of complex numbers in various applications.
-
Roots of Complex Numbers
Finding roots of complex numbers involves using De Moivre's theorem, which states that \((r(\cos \theta + i \sin \theta))^n = r^n (\cos n\theta + i \sin n\theta)\). This theorem helps in calculating powers and roots of complex numbers.
-
Applications in Engineering
Imaginary and complex numbers are extensively used in engineering fields, particularly in signal processing, control systems, and electrical engineering. They help in analyzing and solving differential equations, representing waveforms, and more.
-
History of Imaginary Numbers
The concept of imaginary numbers has a rich history, dating back to the work of mathematicians like Girolamo Cardano and Rafael Bombelli. Over time, these numbers have become essential in modern mathematics and science.
Hướng dẫn cách tìm căn bậc hai của số âm, rất phù hợp cho những ai muốn hiểu rõ về số phức và ứng dụng của chúng.
Cách Tìm Căn Bậc Hai của Số Âm
READ MORE:
Hướng dẫn chi tiết về cách tính căn bậc hai của số thực âm, phù hợp với người học muốn hiểu rõ về số phức và ứng dụng của chúng.
Số Phức(7) - Căn bậc hai của số thực âm