Topic square root of negative 8: The square root of negative 8 can be intriguing as it involves imaginary numbers. Learn how to calculate and simplify the square root of negative 8, and explore its significance in mathematics.
Table of Content
Square Root of Negative 8
The square root of a negative number involves imaginary numbers since the square root of a negative number is not defined in the set of real numbers.
Understanding Imaginary Numbers
The square root of -1 is denoted as i, which stands for the imaginary unit. Using this, we can express the square root of any negative number. For example, the square root of -8 can be expressed as:
Calculation Steps
- Factor the number under the square root: \( \sqrt{-8} = \sqrt{8 \cdot -1} \)
- Separate the factors: \( \sqrt{8} \cdot \sqrt{-1} \)
- Simplify the square root of 8: \( 2\sqrt{2} \)
- Combine with the imaginary unit: \( 2\sqrt{2}i \)
Approximate Value
To approximate the value, we can use the decimal equivalent of \( \sqrt{2} \approx 1.414 \):
Graphical Representation
In the complex plane, the number \( 2\sqrt{2}i \) is represented as a point 2.828 units along the imaginary axis.
Additional Information
For further information on how to calculate square roots of negative numbers and explore more examples, you can refer to resources like , , and .
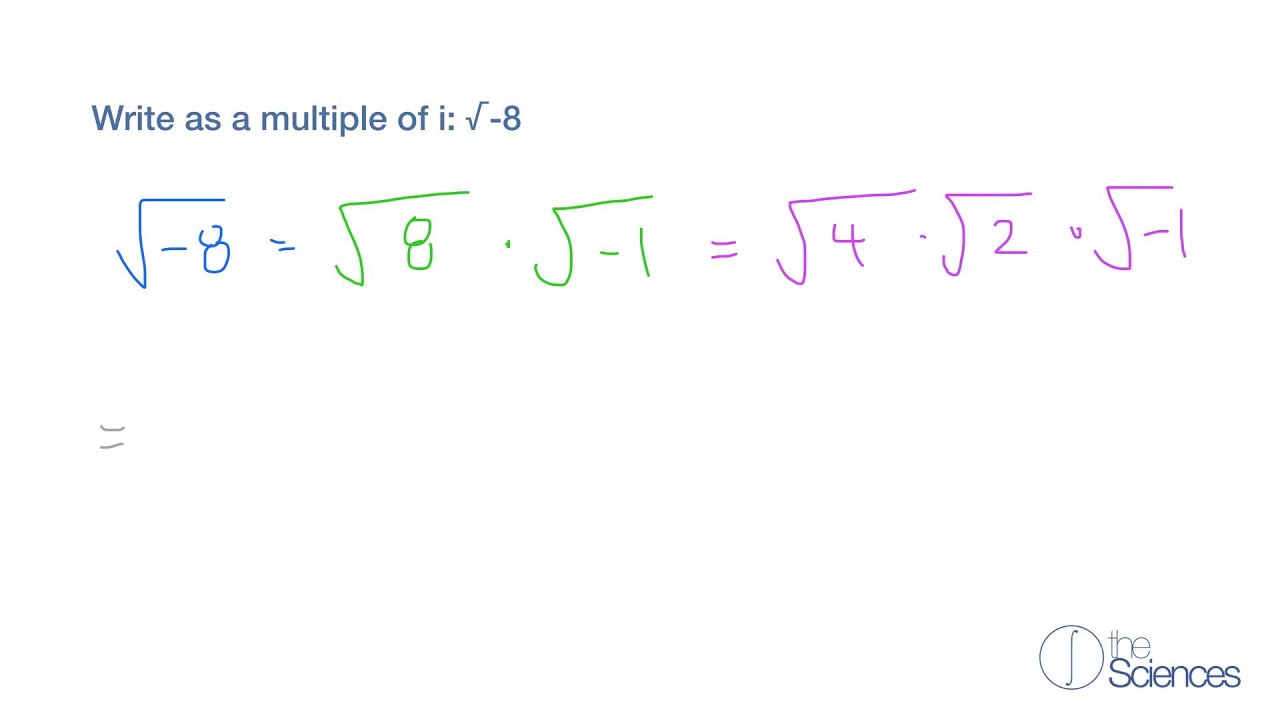
READ MORE:
Introduction
The square root of negative 8 can be an intriguing concept to understand, as it introduces the realm of imaginary numbers. When dealing with the square roots of negative numbers, we enter into the field of complex numbers. The principal square root of a negative number involves the imaginary unit "i," which is defined as the square root of -1. Let's delve into the steps to simplify and calculate the square root of negative 8.
- First, express the square root of -8 as the product of its factors: \( \sqrt{-8} = \sqrt{8 \times -1} \).
- Next, separate the factors under the square root: \( \sqrt{8} \times \sqrt{-1} \).
- Simplify \( \sqrt{8} \): \( \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} \).
- Recognize that \( \sqrt{-1} \) is represented by the imaginary unit "i": \( \sqrt{-1} = i \).
- Combine the simplified parts: \( \sqrt{-8} = 2\sqrt{2} \times i = 2i\sqrt{2} \).
Thus, the square root of -8 is expressed as \( 2i\sqrt{2} \). Understanding this process is crucial in various mathematical and engineering applications where complex numbers play a significant role.
Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. Square roots can be positive or negative, but when we use the radical symbol (√), it usually refers to the principal (non-negative) square root.
Calculating square roots for perfect squares is straightforward. For instance:
- The square root of 16 is 4 because 4 × 4 = 16.
- The square root of 25 is 5 because 5 × 5 = 25.
For non-perfect squares, the square root can be irrational, meaning it cannot be expressed as a simple fraction and its decimal form is non-terminating and non-repeating. For example, the square root of 10 is approximately 3.162.
Square Root of Negative Numbers
Negative numbers do not have real square roots because no real number squared equals a negative number. However, in the realm of complex numbers, we use the imaginary unit 'i', where i² = -1.
To find the square root of a negative number like -8, we express it in terms of 'i':
- First, express -8 as -1 multiplied by 8.
- Then, find the square root of 8 and the square root of -1 separately.
- The square root of 8 is 2√2.
- The square root of -1 is i.
- Thus, the square root of -8 is 2√2i.
This shows how the concept of imaginary numbers extends our ability to find square roots of negative numbers, which is not possible within the set of real numbers alone.
Imaginary Numbers
Imaginary numbers are a fundamental concept in mathematics that extend the real number system to solve equations that do not have solutions within the set of real numbers. The most basic imaginary number is i, which is defined as the square root of -1, written as \(i = \sqrt{-1}\).
When we deal with the square root of a negative number, such as -8, we use the imaginary unit i. The square root of -8 can be expressed as follows:
\[ \sqrt{-8} = \sqrt{8 \cdot -1} = \sqrt{8} \cdot \sqrt{-1} = \sqrt{8} \cdot i = 2\sqrt{2} \cdot i \]
This means that the square root of -8 is \(2\sqrt{2}i\), where \(2\sqrt{2}\) is a real number, and i represents the imaginary unit.
Imaginary numbers are essential for solving quadratic equations with negative discriminants, which do not intersect the x-axis. These solutions involve complex numbers, which are combinations of real and imaginary numbers. A complex number is typically written in the form \(a + bi\), where a and b are real numbers, and i is the imaginary unit.
To better understand imaginary numbers and their applications, it is useful to explore how they are used in solving equations and representing values in the complex plane. The complex plane is a two-dimensional plane where the horizontal axis represents the real part of a number, and the vertical axis represents the imaginary part. This visual representation helps in understanding the operations and properties of complex numbers.
Here is a step-by-step approach to dealing with imaginary numbers:
- Identify the negative number under the square root.
- Express the number as a product of a positive number and -1.
- Separate the square root of the positive number and the square root of -1.
- Simplify the square root of the positive number if possible.
- Multiply the result by i (the square root of -1).
Understanding imaginary numbers allows us to solve a broader range of mathematical problems, making them an invaluable tool in various fields such as engineering, physics, and computer science.
Square Root of Negative 8
Understanding the square root of a negative number, such as -8, involves delving into the concept of imaginary numbers. The square root of a negative number is not a real number, but an imaginary number. Here's a detailed explanation of how to find and understand the square root of -8 step by step:
Start with the expression for the square root of -8:
$$ \sqrt{-8} $$
Rewrite -8 as the product of -1 and 8:
$$ \sqrt{-8} = \sqrt{-1 \times 8} $$
Separate the square root of the product into the product of the square roots:
$$ \sqrt{-1 \times 8} = \sqrt{-1} \times \sqrt{8} $$
Identify the square root of -1, which is the imaginary unit \( i \):
$$ \sqrt{-1} = i $$
Simplify the square root of 8:
$$ \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2\sqrt{2} $$
Combine the results:
$$ \sqrt{-8} = i \times 2\sqrt{2} = 2i\sqrt{2} $$
Thus, the square root of -8 is expressed in terms of imaginary numbers as:
$$ 2i\sqrt{2} $$
If you need to approximate the value, \( \sqrt{2} \approx 1.414 \), so:
$$ 2i\sqrt{2} \approx 2i \times 1.414 \approx 2.828i $$
Therefore, the approximate value of the square root of -8 is:
$$ \pm 2.828i $$
Decimal Approximation
The square root of a negative number involves an imaginary component. When we find the square root of -8, we can express it in terms of the imaginary unit 'i'.
Firstly, we rewrite -8 as -1 * 8 and use the property of square roots:
- √(-8) = √(-1 * 8) = √(-1) * √(8)
- Since √(-1) = i, we get √(-8) = i * √(8)
Now, we simplify √(8):
- 8 can be factored into 4 * 2, so √(8) = √(4 * 2) = √(4) * √(2) = 2√(2)
Thus, we have:
- √(-8) = i * 2√(2) = 2i√(2)
Next, we approximate the value of √(2):
- √(2) is approximately 1.414
- So, 2√(2) ≈ 2 * 1.414 = 2.828
Therefore, the square root of -8 in decimal form is approximately:
- √(-8) ≈ 2.828i
This decimal approximation allows for easier application in various fields, including engineering and physics, where precise numerical values are often required.
Using online calculators, such as those provided by Mathway and Math Warehouse, can simplify these computations, providing exact and approximate forms for complex roots. These tools are invaluable for verifying results and understanding the step-by-step process of finding square roots of negative numbers.
Examples and Applications
Imaginary numbers, including the square root of negative 8, play a significant role in various fields. Here are some practical examples and applications:
- Electrical Engineering: Complex numbers are used to analyze and design electrical circuits, especially those involving alternating current (AC). They help in understanding impedance, phase relationships, and resonance phenomena. For instance, the square root of -8, expressed as 2i√2, can be used to model certain AC circuit behaviors.
- Quantum Mechanics: In quantum mechanics, complex numbers describe the state of particles and probability amplitudes. The use of √-8 as part of complex numbers allows for the representation of quantum states and the calculation of observables in wave functions.
- Signal Processing: Complex numbers are crucial in signal processing for analyzing and manipulating signals. They are used in Fourier transforms, which decompose signals into their frequency components. The term 2i√2 can appear in the context of these transformations and filtering operations.
- Control Theory: Control systems often use complex numbers to analyze system stability and behavior. Imaginary numbers help in plotting poles and zeros on the complex plane, providing insights into system dynamics and stability. For example, the square root of -8 can be used in the analysis of feedback systems and transfer functions.
- Fractal Geometry: The Mandelbrot set and other fractals use complex numbers to generate intricate patterns. The iterative processes that create these fractals often involve complex numbers, including terms like 2i√2, showcasing their beauty and complexity in mathematical art.
These applications highlight the importance of imaginary numbers in solving real-world problems and advancing technology. Understanding the square root of negative numbers opens up numerous possibilities in science and engineering, demonstrating the practical relevance of these abstract mathematical concepts.
Calculators and Tools
Several online calculators and tools can assist in computing the square root of negative numbers, including -8. These tools simplify the process and provide accurate results quickly. Below are some recommended calculators and how to use them:
-
Mathway:
Mathway offers a comprehensive square root calculator that handles both real and imaginary numbers. To use it:
- Go to the Mathway Square Root Calculator.
- Enter "-8" in the input field.
- Click the blue arrow to calculate the square root. Mathway will show the result as \(2i\sqrt{2}\) and provide a step-by-step explanation.
-
Omni Calculator:
Omni Calculator provides an easy-to-use interface for finding the square roots of both positive and negative numbers. Follow these steps:
- Visit the Omni Calculator Square Root page.
- Input "-8" in the designated field.
- The calculator will display the result \(2i\sqrt{2}\) along with a decimal approximation.
-
Mathwarehouse:
Mathwarehouse's square root calculator simplifies complex numbers and provides detailed results. Here's how to use it:
- Navigate to the Mathwarehouse Square Root Calculator.
- Type "-8" into the text box.
- Click "Calculate" to get the simplified form \(2i\sqrt{2}\) and a decimal approximation.
-
US Calculator:
This tool is straightforward and user-friendly. To find the square root of -8:
- Go to the US Calculator Square Root page.
- Enter "-8" in the input box.
- Press "Calculate" to view the result as \(2i\sqrt{2}\).
Using these calculators can simplify the process of finding the square roots of negative numbers, making complex mathematical concepts more accessible.

Conclusion
Understanding the square root of negative numbers, such as -8, introduces the fascinating concept of imaginary numbers. By expressing negative square roots using the imaginary unit \( i \), which is defined as \(\sqrt{-1}\), we can solve and work with these otherwise non-real numbers. The square root of -8 simplifies to \(2i\sqrt{2}\), which highlights the elegance and utility of complex numbers in mathematical problem-solving.
Imaginary numbers are not just abstract concepts but have practical applications in various fields including engineering, physics, and advanced mathematics. They allow for the modeling of phenomena that cannot be represented using only real numbers, making them indispensable in theoretical and applied sciences.
Furthermore, with the advent of advanced calculators and online tools, performing calculations involving imaginary numbers has become more accessible. Tools such as graphing calculators and online platforms like Mathway provide step-by-step solutions, making it easier for students and professionals to engage with complex numbers.
In conclusion, the study of imaginary numbers and their applications broadens our understanding of mathematics and its capabilities. By embracing these concepts, we can solve more complex problems and appreciate the depth and beauty of mathematical theory.
Hướng dẫn - Cách đơn giản hóa căn bậc hai của số âm sử dụng đơn vị ảo i ví dụ 8
READ MORE:
Cách Đơn Giản Hóa Căn Bậc Hai Âm: -sqrt(8)