Topic square root of negative 6: Understanding the square root of negative 6 involves delving into the realm of complex numbers. This concept, rooted in mathematical principles, can be explained using imaginary units. In this article, we explore the theoretical background, practical applications, and step-by-step methods to simplify and compute complex square roots.
Table of Content
- Square Root of Negative 6
- Introduction to Square Roots
- Understanding Negative Square Roots
- Methods to Calculate Square Roots
- Properties and Applications of Square Roots
- Square Roots in Mathematics and Physics
- Properties and Applications of Square Roots
- Methods to Calculate Square Roots
- Common Square Roots and Their Values
- Babylonian Method for Square Root Calculation
- Square Root Calculation Using Calculators
- Practical Examples and Problem Solving
- Conclusion
- YOUTUBE:
Square Root of Negative 6
The square root of negative 6 is not a real number because the square root of a negative number is an imaginary number. This concept can be better understood using complex numbers.
Definition
A square root of a number \( a \) is a number \( x \) such that \( x^2 = a \). For real numbers, this definition applies directly. However, for negative numbers, we need to use imaginary numbers.
Imaginary Numbers
The imaginary unit is denoted as \( i \), where \( i \) is defined as \( \sqrt{-1} \). Therefore, the square root of -6 can be expressed using \( i \) as follows:
\[ \sqrt{-6} = \sqrt{6} \cdot \sqrt{-1} = \sqrt{6} \cdot i \]
Calculation
Using the property of imaginary numbers:
\[ \sqrt{-6} = \sqrt{6} \cdot i \approx 2.449 \cdot i \]
Applications
Understanding the square root of negative numbers is crucial in fields such as electrical engineering, signal processing, and quantum mechanics where complex numbers are extensively used.
Examples of Square Roots
- The square root of 81 is \( \pm 9 \).
- The square root of 25 is \( \pm 5 \).
- The square root of 100 is \( \pm 10 \).
- The square root of 10 is approximately \( \pm 3.162 \).
Additional Resources
For more information, you can explore various online square root calculators and resources to understand how to calculate and simplify square roots, including complex and imaginary numbers.

READ MORE:
Introduction to Square Roots
Square roots are fundamental in mathematics, representing a value that, when multiplied by itself, yields the original number. For example, the square root of 9 is 3, because 3 × 3 = 9. The concept of square roots extends to both positive and negative numbers, though the square roots of negative numbers involve imaginary numbers.
To understand square roots better, let's delve into some important concepts:
- Definition: The square root of a number \(a\) is a number \(x\) such that \(x^2 = a\). For instance, \( \sqrt{25} = 5 \) because \(5^2 = 25\).
- Imaginary Numbers: The square root of a negative number involves imaginary units. For example, the square root of -6 is written as \( \sqrt{-6} = \sqrt{6} \cdot i \), where \(i\) is the imaginary unit (\(i^2 = -1\)).
Square roots are used in various mathematical applications, including solving quadratic equations and analyzing geometrical shapes. They are also critical in higher-level mathematics, such as calculus and complex number theory.
| Number | Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
Understanding square roots can enhance problem-solving skills and provide a deeper insight into mathematical principles.
Understanding Negative Square Roots
In mathematics, the square root of a negative number introduces the concept of imaginary numbers. While square roots of positive numbers are straightforward, negative numbers require a different approach.
To understand negative square roots, we need to introduce the imaginary unit, denoted as i, where \(i = \sqrt{-1}\). This allows us to express the square root of any negative number as a product involving i.
For example, the square root of -6 can be written as:
\[
\sqrt{-6} = \sqrt{6} \cdot \sqrt{-1} = \sqrt{6} \cdot i = i\sqrt{6}
\]
Here is a step-by-step explanation:
- Identify the negative number under the square root, such as -6.
- Separate the negative sign and express it as \(\sqrt{-1}\), which is equal to i.
- Take the square root of the positive part of the number. For 6, it remains as \(\sqrt{6}\).
- Combine the results to form \(i\sqrt{6}\).
Understanding this concept helps in various fields such as engineering, physics, and complex number theory, where imaginary numbers are frequently used. It is important to note that imaginary numbers are essential for solving certain types of equations that have no real solutions.
Methods to Calculate Square Roots
Calculating square roots can be approached in several ways. Below, we outline some of the most common methods used to find the square root of a number, including manual calculations and the use of calculators.
- Manual Calculation
- Prime Factorization
- Using a Calculator
- Newton's Method
- Estimation and Approximation
Manual Calculation
For small numbers and perfect squares, manual calculation is often straightforward. For instance, the square root of 16 is 4 because \(4^2 = 16\).
Prime Factorization
To find the square root using prime factorization, express the number as a product of prime factors. For example, to find the square root of 36:
- Prime factorize 36: \(36 = 2^2 \times 3^2\)
- Take the square root of each factor: \( \sqrt{36} = \sqrt{2^2 \times 3^2} = 2 \times 3 = 6\)
Using a Calculator
Most modern calculators have a square root function. Simply enter the number and press the square root button (\( \sqrt{} \)). For example, to find the square root of 25, input 25 and press \( \sqrt{} \) to get 5.
Newton's Method
Newton's Method (also known as the Newton-Raphson method) is an iterative process. For finding \( \sqrt{N} \), the formula is:
\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{N}{x_n} \right) \]
Start with an initial guess \( x_0 \), and iterate using the formula until the desired precision is achieved.
Estimation and Approximation
For numbers that are not perfect squares, use estimation to find a close approximation. For example, to find \( \sqrt{10} \):
- Note that \(3^2 = 9\) and \(4^2 = 16\)
- Since 10 is closer to 9, start with 3.1: \(3.1^2 = 9.61\)
- Adjust to get closer to 10, e.g., \(3.2^2 = 10.24\), so the approximation \( \sqrt{10} \approx 3.16 \)
Each of these methods provides a different approach to finding square roots, ranging from simple manual techniques to more complex iterative methods.
Properties and Applications of Square Roots
Square roots are fundamental mathematical operations with various properties and applications across different fields. Understanding these properties helps in solving complex equations and in practical applications such as engineering, physics, and finance.
- Basic Properties
- The square root of a number \(x\) is a value that, when multiplied by itself, gives \(x\).
- Square roots are denoted by the radical symbol \(\sqrt{}\).
- For any non-negative number \(x\), there are two square roots: a positive and a negative (e.g., \(\sqrt{25} = 5\) and \(\sqrt{25} = -5\)).
- Imaginary Numbers
- The square root of a negative number is an imaginary number.
- Imaginary numbers are represented using \(i\), where \(i = \sqrt{-1}\).
- For example, the square root of -6 is represented as \(\sqrt{-6} = \sqrt{6}i\).
- Applications
- Square roots are used in solving quadratic equations.
- They are essential in geometry for finding the lengths of sides of right-angled triangles using the Pythagorean theorem.
- Square roots are utilized in physics to calculate distances and speeds under uniform acceleration.
- In finance, they are used in the calculation of standard deviation and variance in statistics, which measure the spread of a set of values.
Understanding the properties and applications of square roots enhances problem-solving skills and enables their effective use in various scientific and real-world scenarios.

Square Roots in Mathematics and Physics
The concept of square roots is fundamental in both mathematics and physics, where it has a variety of applications and properties.
In mathematics, the square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). For example, the square root of 9 is 3, since \( 3 \times 3 = 9 \). Square roots can be both positive and negative; thus, \( \sqrt{9} = 3 \) and \( \sqrt{9} = -3 \). However, when dealing with negative numbers, the square root is not a real number but an imaginary one. For instance, the square root of -6 is expressed as \( \sqrt{-6} = i\sqrt{6} \), where \( i \) is the imaginary unit defined as \( \sqrt{-1} \).
Properties and Applications of Square Roots
- Non-Negative Property: The square root function only returns non-negative results for non-negative inputs in real numbers.
- Product Property: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). This is useful in simplifying complex expressions.
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), provided \( b \neq 0 \).
- Application in Geometry: Square roots are used to determine the side length of a square given its area and in the Pythagorean theorem to find the length of a hypotenuse.
- Application in Physics: Square roots appear in various formulas, such as those involving the calculation of energy in quantum mechanics, wave functions, and standard deviations in statistics.
Methods to Calculate Square Roots
There are several methods to calculate square roots, ranging from manual techniques to algorithmic approaches implemented in calculators and computers.
- Prime Factorization: By expressing the number as a product of prime factors, you can simplify the square root calculation.
- Babylonian Method (Hero's Method): An iterative method that improves an initial guess through averaging.
- Using Calculators: Most scientific calculators have a square root function that allows for quick computation.
- Newton's Method: An efficient numerical technique for finding successively better approximations to the roots of a real-valued function.
Common Square Roots and Their Values
Understanding the values of common square roots is fundamental in mathematics. Below is a table of perfect squares and their corresponding square roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
In addition to these perfect squares, we also have common square roots that are not whole numbers:
- √2 ≈ 1.414
- √3 ≈ 1.732
- √5 ≈ 2.236
- √6 ≈ 2.449
- √7 ≈ 2.646
- √8 ≈ 2.828
- √10 ≈ 3.162
When dealing with negative numbers, their square roots involve imaginary numbers. For example, the square root of -1 is represented by the imaginary unit 'i'. Hence, the square root of -6 can be written as:
√-6 = √6 * √-1 = 2.449i
Here, 'i' is used to denote the imaginary unit where i² = -1. Understanding these values is crucial for various applications in mathematics and science.

Babylonian Method for Square Root Calculation
The Babylonian method, also known as Heron's method, is an ancient technique for approximating the square root of a number. This iterative method is simple yet effective and can be used to find the square root of any positive number.
Here is a step-by-step explanation of the Babylonian method:
- Start with a number \( S \) for which you want to find the square root.
- Make an initial guess \( x_0 \). A reasonable starting point is \( x_0 = \frac{S}{2} \) or any positive number close to the actual square root.
- Apply the iterative formula:
\[ x_{n+1} = \frac{x_n + \frac{S}{x_n}}{2} \]
This formula is derived from the idea of averaging the number \( x_n \) and \( \frac{S}{x_n} \). - Repeat step 3 until the difference between \( x_{n+1} \) and \( x_n \) is less than a predetermined tolerance level (e.g., \( \epsilon = 0.0001 \)).
The iteration process ensures that with each step, the estimate gets closer to the actual square root. Here is an example to illustrate this method:
| Iteration (n) | Guess (xn) |
|---|---|
| 0 | Initial guess: \( x_0 = \frac{S}{2} \) |
| 1 | \( x_1 = \frac{x_0 + \frac{S}{x_0}}{2} \) |
| 2 | \( x_2 = \frac{x_1 + \frac{S}{x_1}}{2} \) |
| ... | ... |
For example, to find the square root of 25:
- Let \( S = 25 \).
- Initial guess: \( x_0 = 12.5 \).
- First iteration: \( x_1 = \frac{12.5 + \frac{25}{12.5}}{2} = 7.25 \).
- Second iteration: \( x_2 = \frac{7.25 + \frac{25}{7.25}}{2} \approx 5.349 \).
- Third iteration: \( x_3 = \frac{5.349 + \frac{25}{5.349}}{2} \approx 5.011 \).
- Continue iterations until the change is smaller than the tolerance level, eventually converging to 5.
This method is effective due to its quadratic convergence, meaning that the number of correct digits approximately doubles with each iteration.
The Babylonian method is not only a historical technique but also serves as the foundation for modern algorithms used in calculators and computers to compute square roots.
Square Root Calculation Using Calculators
Calculators are essential tools for quickly and accurately finding square roots, especially for complex or non-perfect square numbers. Here is a step-by-step guide to calculating square roots using calculators:
-
Accessing the Square Root Function:
- Most calculators have a dedicated square root (√) button. On scientific calculators, this is usually labeled as
√orsqrt. - If using an online calculator, such as those available on or , find the square root function in the calculator interface.
- Most calculators have a dedicated square root (√) button. On scientific calculators, this is usually labeled as
-
Input the Number:
- Enter the number for which you want to calculate the square root. For example, to find the square root of 36, press
3followed by6.
- Enter the number for which you want to calculate the square root. For example, to find the square root of 36, press
-
Calculate the Square Root:
- Press the square root button
√. The calculator will display the result. For 36, the display should show6since √36 = 6.
- Press the square root button
-
Understanding the Result:
- If the number is a perfect square, the result will be an integer. For example, √25 = 5.
- If the number is not a perfect square, the calculator will display a decimal approximation. For example, √10 ≈ 3.162278.
Calculators are also capable of handling more complex inputs and can provide imaginary solutions for negative numbers:
-
Square Roots of Negative Numbers:
- For negative numbers, such as finding the square root of -6, the calculator will display an imaginary number result. For example, √-6 = 0 + 2.44949i.
- This is because the square root of a negative number is not a real number, but an imaginary one, denoted by
i.
Using these methods, you can efficiently calculate the square roots of both positive and negative numbers, whether they are perfect squares or not.
Practical Examples and Problem Solving
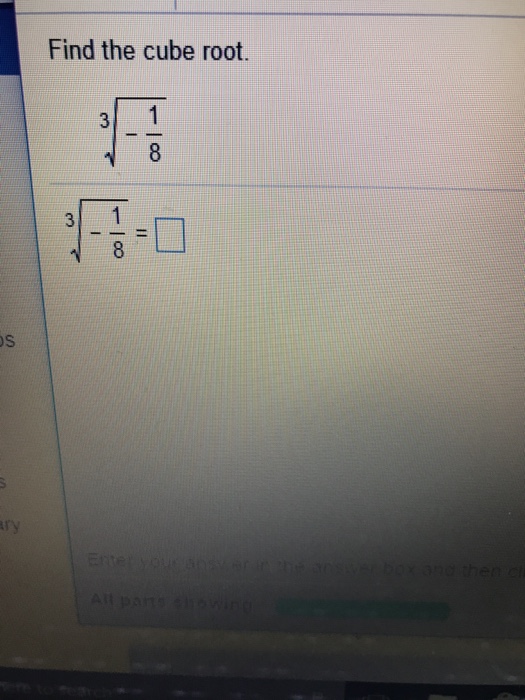
Understanding the square root of negative numbers requires knowledge of imaginary numbers. The square root of -6 can be represented as \( \sqrt{-6} = \sqrt{6} \cdot i \), where \( i \) is the imaginary unit defined by \( i^2 = -1 \).
Example 1: Simplifying Expressions
Let's simplify the expression \( \sqrt{-6} \).
- Identify the negative square root: \( \sqrt{-6} \).
- Express in terms of \( i \): \( \sqrt{-6} = \sqrt{6} \cdot i \).
Example 2: Solving Quadratic Equations
Consider the quadratic equation \( x^2 + 6 = 0 \).
- Isolate the \( x^2 \) term: \( x^2 = -6 \).
- Take the square root of both sides: \( x = \pm \sqrt{-6} \).
- Express the solutions in terms of \( i \): \( x = \pm \sqrt{6} \cdot i \).
Example 3: Complex Number Operations
Let's multiply \( \sqrt{-6} \) by \( \sqrt{-3} \).
- Express each square root in terms of \( i \):
- \( \sqrt{-6} = \sqrt{6} \cdot i \)
- \( \sqrt{-3} = \sqrt{3} \cdot i \)
- Multiply the expressions:
- \( \sqrt{6} \cdot i \times \sqrt{3} \cdot i = \sqrt{6 \cdot 3} \cdot i^2 \)
- \( \sqrt{18} \cdot -1 = -\sqrt{18} = -3\sqrt{2} \)
Practice Problems
- Simplify \( \sqrt{-8} \).
- Solve the equation \( x^2 + 8 = 0 \).
- Multiply \( \sqrt{-2} \) by \( \sqrt{-5} \).
By practicing these problems, you can gain a better understanding of how to handle square roots of negative numbers and apply them in various mathematical contexts.
Conclusion
The concept of square roots extends beyond simple arithmetic, especially when dealing with negative numbers. The square root of negative 6, represented as \( \sqrt{-6} \), highlights the necessity of complex numbers in mathematics. This root can be expressed as \( \sqrt{6} \cdot i \), where \( i \) is the imaginary unit defined by \( i^2 = -1 \).
Throughout this guide, we have explored the fundamental principles of square roots, the methods to calculate them, and their properties and applications. We delved into specific techniques like the Babylonian method and the use of calculators for efficient calculation. Additionally, practical examples demonstrated the real-world applications and problem-solving approaches involving square roots.
Understanding square roots, including those of negative numbers, is crucial for various fields such as engineering, physics, and complex number theory. This comprehensive guide aims to equip readers with the knowledge and tools necessary to navigate and apply these mathematical concepts effectively.
In conclusion, mastering square roots, especially in the realm of complex numbers, opens up a deeper appreciation and capability in mathematical problem-solving and theoretical exploration.
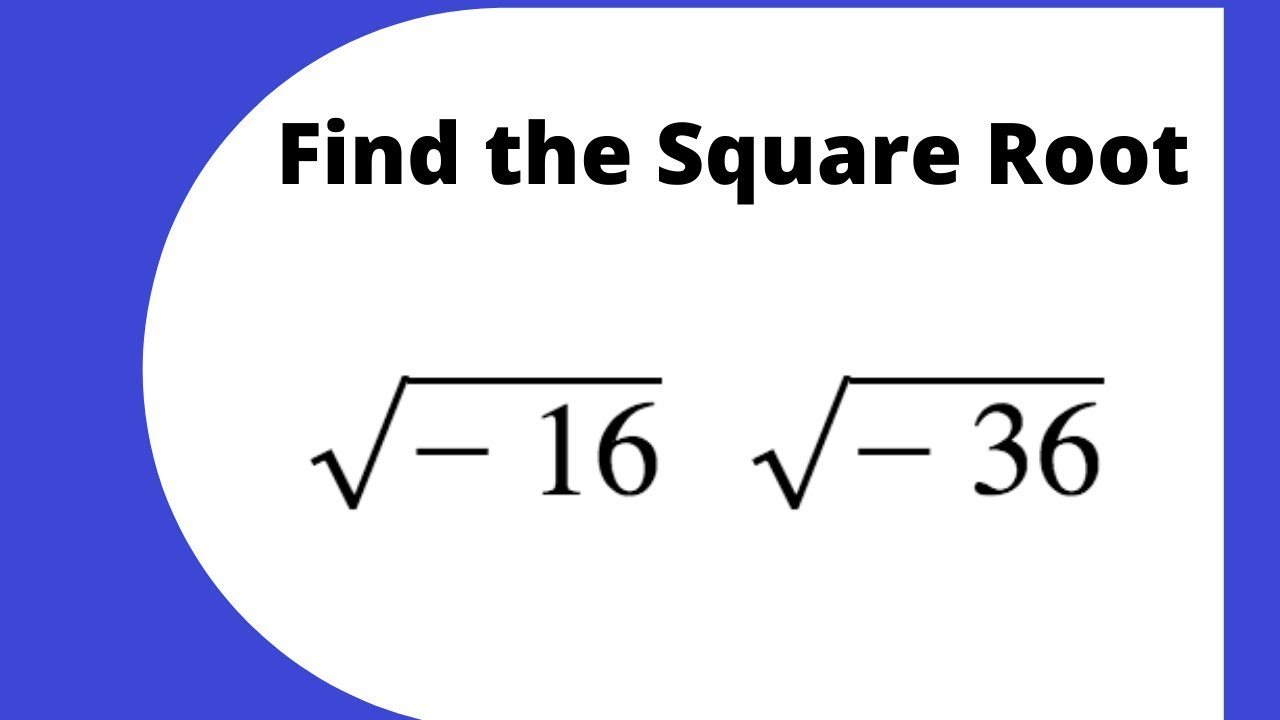
Tại sao căn bậc hai của 36 chỉ là 6 dương
READ MORE:
A2 - (6) Số phức; căn bậc hai của số âm