Topic square root 300: Discover the fascinating world of the square root of 300 in this comprehensive article. Learn various calculation methods, understand its properties, and explore real-life applications. Whether you're a math enthusiast or just curious about numbers, delve into the intricacies of this mathematical concept with us.
Table of Content
- Square Root of 300
- Introduction to Square Root of 300
- Understanding the Mathematical Calculation
- Methods to Calculate Square Root of 300
- Decimal Representation and Approximations
- Is Square Root of 300 Rational or Irrational?
- Properties and Mathematical Relationships
- Historical Context and Significance
- Real-Life Applications and Examples
- Conclusion: Key Takeaways about Square Root of 300
- YOUTUBE: Khám phá cách đơn giản hóa căn bậc hai của 300 một cách dễ hiểu và chi tiết trong video này. Học cách tính toán và áp dụng trong thực tế.
Square Root of 300
The square root of 300 is a number which, when multiplied by itself, equals 300. It is an irrational number, often represented in both its radical form and its decimal form.
Decimal Form
The square root of 300 in decimal form is approximately \(17.3205\).
Radical Form
The square root of 300 in its simplest radical form is \(10\sqrt{3}\).
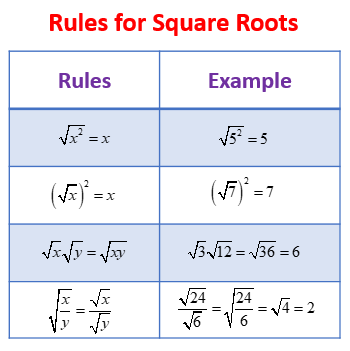
Calculation Methods
There are several methods to calculate the square root of 300:
- Prime Factorization Method: By expressing 300 as the product of its prime factors, we get \(300 = 2^2 \times 3 \times 5^2\). Therefore, \( \sqrt{300} = \sqrt{2^2 \times 3 \times 5^2} = 10\sqrt{3}\).
- Long Division Method: This method is particularly useful for finding the square root of numbers that are not perfect squares. Using this method, the square root of 300 is found to be approximately 17.3205.
Examples and Applications
- Area of a Square: If the area of a square is 90,000 sq. cm, the length of each side of the square is \( \sqrt{90000} = 300 \) cm.
- Radius of a Circle: For a circle with an area of \(300\pi\) square inches, the radius is \( \sqrt{300} = 17.321 \) inches.
- Quadratic Equation: Solving the equation \( x^2 - 300 = 0 \) gives \( x = \pm \sqrt{300} = \pm 17.3205 \).
Additional Information
The square root of 300 is an irrational number because it cannot be expressed as a simple fraction. Its decimal representation is non-terminating and non-repeating.
Table of n-th Roots of 300
| n | n-th Root of 300 |
|---|---|
| 2 | 17.3205 |
| 3 | 6.6943 |
| 4 | 4.1618 |
| 5 | 3.1291 |
| 6 | 2.5873 |
| 7 | 2.2588 |
| 8 | 2.0400 |
| 9 | 1.8847 |
| 10 | 1.7689 |

READ MORE:
Introduction to Square Root of 300
The square root of 300 is a mathematical value denoted as √300. It represents the value which, when multiplied by itself, gives the number 300. Understanding the square root of 300 involves exploring its properties and various methods to calculate it.
In mathematical terms, √300 is an irrational number, meaning it cannot be expressed as a simple fraction. It falls between whole numbers 17 and 18, indicating its approximate value lies around 17.32. This number is crucial in fields such as geometry, physics, and engineering, where precise calculations are essential.
To calculate √300, several methods can be employed, including the prime factorization method, the estimation method using successive approximations, or using a scientific calculator for accuracy.
Understanding the Mathematical Calculation
To calculate the square root of 300, several methods can be used depending on the level of precision required:
- Prime Factorization Method: Start by finding the prime factors of 300 (2, 2, 3, 5, 5). Pair them up (2, 2), (5, 5), take one from each pair, and multiply: √(2 * 5) = √10. Since there's one 2 left, the square root of 300 is 10√3.
- Estimation Method: Begin with an initial guess, such as √289 = 17. Adjust based on whether the square of the estimate is too high or too low relative to 300.
- Using a Calculator: For precise results, enter √300 directly into a scientific calculator, yielding approximately 17.32.
These methods provide various approaches to understanding and calculating the square root of 300, each suitable for different contexts and needs.
Methods to Calculate Square Root of 300
There are several methods to calculate the square root of 300, ranging from manual calculation techniques to the use of calculators and software. Below are some of the most common methods:
1. Prime Factorization Method
This method involves breaking down the number 300 into its prime factors and then simplifying the square root.
- Factorize 300: \(300 = 2^2 \times 3 \times 5^2\).
- Express the square root in terms of these factors: \[ \sqrt{300} = \sqrt{2^2 \times 3 \times 5^2} = \sqrt{2^2} \times \sqrt{3} \times \sqrt{5^2}. \]
- Simplify the expression: \[ \sqrt{300} = 2 \times \sqrt{3} \times 5 = 10\sqrt{3}. \]
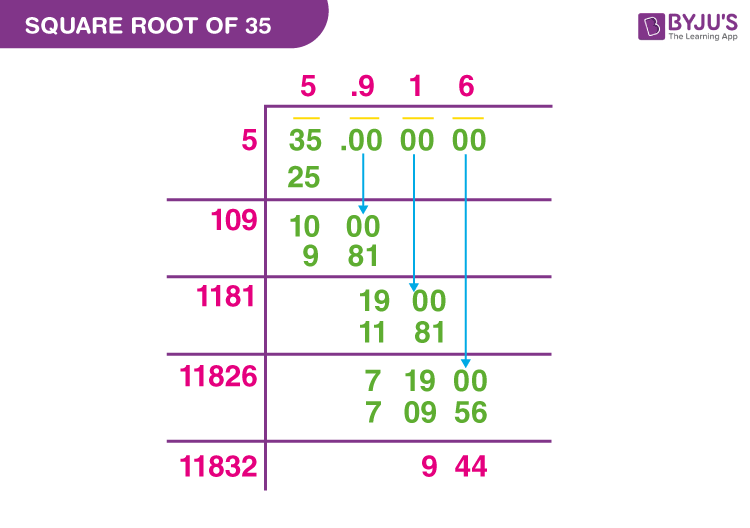
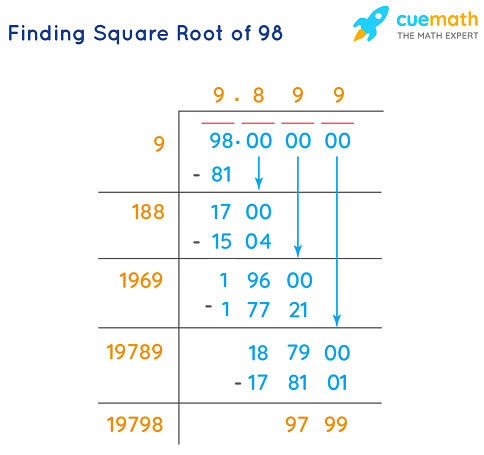
2. Long Division Method
The long division method is a manual technique that provides an accurate decimal representation of the square root.
- Pair the digits of the number from right to left: 300 becomes 3 00.
- Find the largest number whose square is less than or equal to the first pair (3): \[ 1^2 = 1 \quad (\text{since } 2^2 = 4 \text{ is greater than } 3). \]
- Subtract 1 from 3 to get 2 and bring down the next pair of zeros to make it 200.
- Double the quotient obtained so far (1) and place it as the new divisor with a blank digit to its right (i.e., 20_).
- Find the largest digit (X) to fill in the blank such that \(20X \times X \leq 200\): \[ 202 \times 2 = 404 \quad (\text{too large, so use 1}). \]
- Place 1 in the quotient and subtract \(201\) from \(200\), then bring down another pair of zeros (00) to get 9900.
- Continue the process until you reach the desired decimal places.
3. Newton's Method (Iterative Approximation)
Newton's method, also known as the Newton-Raphson method, is an iterative process that starts with an initial guess and converges to the actual square root.
- Start with an initial guess \( x_0 \). For simplicity, let's use \( x_0 = 10 \) (since \( 10^2 = 100 \), which is close to 300).
- Apply the formula: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{300}{x_n} \right). \]
- Iterate until the values converge to a stable number:
- First iteration: \[ x_1 = \frac{1}{2} \left( 10 + \frac{300}{10} \right) = \frac{1}{2} (10 + 30) = 20. \]
- Second iteration: \[ x_2 = \frac{1}{2} \left( 20 + \frac{300}{20} \right) = \frac{1}{2} (20 + 15) = 17.5. \]
- Continue this process until \( x_n \) stabilizes around 17.32.
4. Using a Calculator
The simplest and most straightforward method to find the square root of 300 is to use a scientific calculator:
- Turn on the calculator.
- Enter the number 300.
- Press the square root (√) button.
- Read the displayed result: approximately 17.32.
5. Software Tools
Various software tools and programming languages can compute the square root of 300 efficiently:
- Using Python:
import math print(math.sqrt(300)) # Output: 17.320508075688775 - Using Excel:
=SQRT(300)
Decimal Representation and Approximations
The square root of 300 can be represented in decimal form, and this section will provide detailed steps to understand its decimal representation and approximations.
Exact Value and Initial Approximation
The exact value of the square root of 300 is an irrational number. Therefore, it cannot be expressed as a simple fraction and has an infinite number of decimal places without repeating.
The square root of 300 is approximately:
\[
\sqrt{300} \approx 17.320508075688775
\]
Step-by-Step Decimal Calculation
Using the long division method, we can approximate the square root of 300 step by step:
- Start by pairing the digits of 300 from right to left: 3 00.
- Find the largest number whose square is less than or equal to 3: \[ 1^2 = 1. \] The first digit of the quotient is 1.
- Subtract 1 from 3 and bring down the next pair of zeros to get 200.
- Double the quotient so far (1) to get 2 and place it as the new divisor (20_).
- Find the largest digit (X) such that \(20X \times X \leq 200\). Here, X is 1: \[ 201 \times 1 = 201. \]
- Subtract 201 from 200 to get -1 and bring down another pair of zeros to get 9900.
- Double the current quotient (11) to get 22 and find the largest digit X such that \(220X \times X \leq 9900\). Here, X is 4: \[ 2244 \times 4 = 8976. \]
- Continue this process to get more decimal places, resulting in an approximate value: \[ 17.3205. \]
Using a Calculator
To get a quick and precise value, you can use a scientific calculator:
- Enter 300.
- Press the square root (√) button.
- The calculator displays: 17.320508075688775.
Approximation Methods
When a high level of precision is not required, you can use different approximation methods:
- Rounding: For simplicity, you can round the value to a specific decimal place. For instance, rounding to two decimal places gives: \[ \sqrt{300} \approx 17.32. \]
- Using fractions: You can use a nearby fraction to approximate the square root: \[ \sqrt{300} \approx \frac{173}{10} = 17.3. \]
Using Software Tools
Various software tools can help compute and verify the square root of 300:
- Python: Use the
mathmodule:import math print(math.sqrt(300)) # Output: 17.320508075688775 - Excel: Use the formula:
=SQRT(300)
Both methods will give you the precise decimal representation of the square root of 300.

Is Square Root of 300 Rational or Irrational?
To determine whether the square root of 300 is rational or irrational, we need to understand the definitions and properties of rational and irrational numbers.
Definitions
- Rational Numbers: A rational number can be expressed as a fraction \(\frac{p}{q}\) where \(p\) and \(q\) are integers, and \(q \neq 0\).
- Irrational Numbers: An irrational number cannot be expressed as a simple fraction. It has non-repeating, non-terminating decimal expansion.
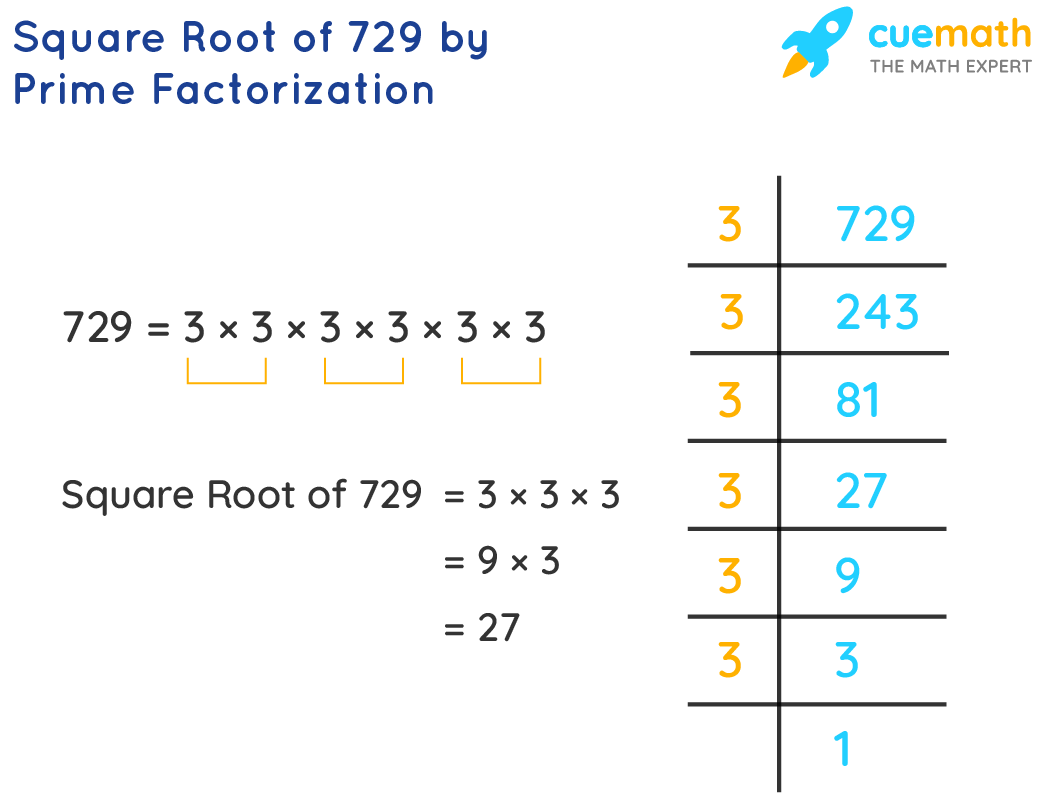
Prime Factorization of 300
We can use the prime factorization method to help determine the nature of the square root of 300.
- Prime factorize 300: \[ 300 = 2^2 \times 3 \times 5^2. \]
- Express the square root of 300 in terms of its prime factors: \[ \sqrt{300} = \sqrt{2^2 \times 3 \times 5^2} = \sqrt{2^2} \times \sqrt{3} \times \sqrt{5^2} = 2 \times \sqrt{3} \times 5 = 10\sqrt{3}.
Analyzing the Expression
We need to determine if \(10\sqrt{3}\) is a rational or irrational number.
- \(\sqrt{3}\) is known to be an irrational number because it cannot be expressed as a fraction and its decimal expansion is non-repeating and non-terminating.
- Multiplying an irrational number (\(\sqrt{3}\)) by a rational number (10) still results in an irrational number.
Conclusion
Based on the above analysis, we can conclude that:
\[
\sqrt{300} = 10\sqrt{3}
\]
is an irrational number because it cannot be expressed as a fraction and its decimal expansion does not terminate or repeat.
Properties and Mathematical Relationships
The square root of 300 has several interesting properties and mathematical relationships. Understanding these can provide deeper insights into its nature and applications in various mathematical contexts.
Basic Properties
- Non-negative: The square root of a non-negative number is also non-negative. Hence, \(\sqrt{300} \geq 0\).
- Product Property: The square root of a product is equal to the product of the square roots: \[ \sqrt{300} = \sqrt{3 \times 100} = \sqrt{3} \times \sqrt{100} = \sqrt{3} \times 10 = 10\sqrt{3}.
- Exponential Form: The square root can be expressed in exponential form as: \[ \sqrt{300} = 300^{\frac{1}{2}}.
- Irrationality: As established earlier, \(\sqrt{300}\) is irrational, meaning its decimal expansion is non-terminating and non-repeating.
Mathematical Relationships
There are various mathematical relationships involving the square root of 300:
- Square Relationship: If \(x = \sqrt{300}\), then \(x^2 = 300\). This means: \[ (\sqrt{300})^2 = 300.
- Proportional Relationships: \(\sqrt{300}\) can be used to understand proportions involving 300. For example, in geometry, if the area of a square is 300 square units, then the side length is \(\sqrt{300}\) units.
- Relation to Other Roots: The square root of 300 is related to other roots and powers. For instance: \[ 300^{\frac{1}{2}} = (30 \times 10)^{\frac{1}{2}} = \sqrt{30 \times 10} = \sqrt{30} \times \sqrt{10}.
Geometric Interpretation
The square root of 300 can be visualized geometrically:
- Square Area: A square with an area of 300 square units has each side of length \(\sqrt{300}\) units.
- Diagonal of a Rectangle: For a rectangle with sides 10 and \(\sqrt{30}\), the diagonal is \(\sqrt{10^2 + (\sqrt{30})^2} = \sqrt{100 + 30} = \sqrt{130}\), highlighting a relationship with \(\sqrt{300}\).
Applications in Real-Life Problems
Understanding the properties of \(\sqrt{300}\) can aid in solving real-life problems:
- Engineering: Calculations involving materials and dimensions often require square roots, including \(\sqrt{300}\).
- Physics: Various physical formulas and principles, such as those involving area and force, use square roots.
In summary, the square root of 300, while primarily a mathematical concept, has broad applications and relationships that extend into various fields of science and everyday problem-solving.
Historical Context and Significance
The concept of square roots has a rich historical background, deeply rooted in ancient civilizations. The earliest recorded methods of calculating square roots date back to the Babylonian era, around 1800-1600 BC. The Babylonians developed a sophisticated algorithm, which involved successive approximations to find the square root of numbers. This method is remarkably similar to the modern-day iterative methods used for the same purpose.
One of the most famous artifacts from this period is the clay tablet YBC 7289, which shows an approximation of the square root of 2 accurate to several decimal places. This artifact highlights the advanced mathematical understanding of the Babylonians.
In ancient Egypt, the Rhind Mathematical Papyrus (circa 1650 BC) provides evidence of methods used to extract square roots. The Egyptians employed a technique based on inverse proportions to approximate square roots, demonstrating their practical approach to solving mathematical problems.
Indian mathematicians also made significant contributions to the understanding of square roots. The Sulba Sutras, dating from around 800-500 BC, contain rules for finding the square root of numbers. Later, Aryabhata, in his work Aryabhatiya (circa 500 AD), provided methods for extracting square roots and solving quadratic equations.
The Greeks further advanced the theory of square roots. The Pythagoreans are credited with the discovery of irrational numbers, including the realization that the square root of a non-square integer is irrational. Euclid's Elements, particularly Book X, systematically explored the properties of irrational numbers, building on earlier discoveries by Theaetetus around 380 BC.
In summary, the historical significance of square roots spans multiple ancient civilizations, each contributing to the development of mathematical methods and theories. From the Babylonians and Egyptians to the Indians and Greeks, the journey of understanding square roots reflects the evolution of mathematical thought over millennia.
Real-Life Applications and Examples
The square root of 300 has various real-life applications across different fields. Here are a few examples and methods where the square root of 300, as well as square roots in general, play a significant role:
-
Architecture and Engineering
In architecture and engineering, square roots are used to calculate dimensions, distances, and structural integrity. For instance, when designing a square area or structure with a specific area, the side length is determined using the square root of the area. If an engineer needs to design a square with an area of 300 square units, they would calculate the side length as \( \sqrt{300} \approx 17.32 \) units.
-
Physics and Gravity
Square roots are also used in physics, especially in formulas related to gravity and motion. For example, the time \( t \) it takes for an object to fall from a certain height \( h \) is given by the formula \( t = \frac{\sqrt{h}}{4} \). If an object is dropped from a height of 300 feet, the time it takes to hit the ground can be calculated as \( t = \frac{\sqrt{300}}{4} \approx 4.33 \) seconds.
-
Finance
In finance, square roots are used to calculate the rate of return on investments over a period of time. The formula to find the annualized return \( R \) over two periods involves the square root: \( R = \sqrt{\frac{V_2}{V_0}} - 1 \), where \( V_0 \) is the initial value and \( V_2 \) is the value after two periods.
-
Distance Measurement
Square roots are crucial in measuring distances between points in two-dimensional (2D) or three-dimensional (3D) space. Using the distance formula derived from the Pythagorean theorem, the distance \( D \) between two points \((x_1, y_1)\) and \((x_2, y_2)\) in 2D is calculated as \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \). For 3D space, the formula extends to \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \).
-
Accident Investigation
In forensic science, particularly in accident investigations, the length of skid marks left by vehicles is used to estimate the speed before braking. The formula involves the square root of the product of a constant and the skid distance: \( \text{Speed} = \sqrt{24 \times \text{Skid Distance}} \). If the skid marks measure 300 feet, the speed can be estimated as \( \sqrt{24 \times 300} \approx 84.85 \) mph.
These examples illustrate how the mathematical concept of square roots extends beyond theoretical calculations to practical, everyday applications in various fields.

Conclusion: Key Takeaways about Square Root of 300
The square root of 300 is an intriguing number with several important mathematical properties and applications. Here are the key takeaways:
- Value and Approximation: The square root of 300 is approximately \(\sqrt{300} \approx 17.3205\).
- Decimal Representation: As an irrational number, the square root of 300 has a non-repeating, non-terminating decimal expansion. It cannot be expressed exactly as a simple fraction.
- Prime Factorization Method: The square root of 300 can be simplified using its prime factors. The prime factorization of 300 is \(2^2 \times 3 \times 5^2\). Thus, \(\sqrt{300} = \sqrt{2^2 \times 3 \times 5^2} = 10\sqrt{3}\).
- Rationality: Since it cannot be expressed as a fraction of two integers, the square root of 300 is classified as an irrational number.
- Mathematical Relationships: The square root function is fundamental in various mathematical operations and is crucial for solving quadratic equations, understanding geometric relationships, and in calculus for finding the rate of change.
- Historical Context: Historically, the concept of square roots dates back to ancient civilizations, where mathematicians sought to understand and compute roots of numbers for practical and theoretical purposes.
- Real-Life Applications: The square root of 300, like other square roots, is used in various real-life scenarios such as calculating areas, in engineering for understanding stress and strain in materials, in physics for wave functions, and in financial models for risk assessment.
Understanding the square root of 300 provides a glimpse into the broader world of mathematics, illustrating both the complexity and the elegance of numerical relationships. Whether approached through manual calculation methods or modern computational tools, the exploration of square roots remains a foundational element of mathematical education and application.
Khám phá cách đơn giản hóa căn bậc hai của 300 một cách dễ hiểu và chi tiết trong video này. Học cách tính toán và áp dụng trong thực tế.
Căn bậc hai của 300, đơn giản hóa căn bậc hai của 300
READ MORE:
Khám phá cách tính toán và ý nghĩa của căn bậc hai của 300 trong video này. Tìm hiểu phương pháp và ứng dụng thực tế một cách dễ hiểu.
Căn Bậc Hai Của 300