Topic what is the square root of 80 simplified: Unlock the secrets to simplifying the square root of 80 with our easy-to-follow guide. Learn the step-by-step process, understand the prime factorization method, and master the techniques to simplify radicals effectively. Perfect for students, educators, and math enthusiasts looking to deepen their understanding and enhance their skills.
Table of Content
- Understanding the Simplified Square Root of 80
- Introduction to Square Roots
- Understanding the Square Root of 80
- Prime Factorization Method
- Step-by-Step Simplification Process
- Breaking Down the Radicals
- Combining the Simplified Factors
- Verifying the Simplified Form
- Practical Applications of Simplifying Square Roots
- Common Mistakes to Avoid
- Advanced Simplification Techniques
- YOUTUBE: Hướng dẫn đơn giản hóa căn bậc hai của 80 bằng cách sử dụng phương pháp phân tích số nguyên tố. Phù hợp cho những ai muốn tìm hiểu toán học cơ bản.
Understanding the Simplified Square Root of 80
The square root of 80 can be simplified by finding the prime factorization of 80 and then simplifying the radical.
Step-by-Step Guide to Simplifying the Square Root of 80
- Find the prime factorization of 80.
- 80 = 2 × 40
- 40 = 2 × 20
- 20 = 2 × 10
- 10 = 2 × 5
- Therefore, 80 = 2 × 2 × 2 × 2 × 5 or 80 = 24 × 5
- Rewrite the square root of 80 using its prime factors:
\(\sqrt{80} = \sqrt{2^4 \times 5}\)
- Simplify the square root by separating the factors inside the radical:
\(\sqrt{80} = \sqrt{2^4} \times \sqrt{5}\)
- Since the square root of 24 is 22 or 4:
\(\sqrt{2^4} = 2^2 = 4\)
- Combine the simplified parts:
\(\sqrt{80} = 4 \sqrt{5}\)
Conclusion
The simplified form of the square root of 80 is \(4 \sqrt{5}\). This means that the square root of 80 can be expressed as 4 times the square root of 5.
READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing a value that, when multiplied by itself, gives the original number. Understanding square roots is crucial for solving various mathematical problems and is widely used in algebra, geometry, and beyond. In this section, we will explore the basics of square roots and the process of simplifying them.
A square root is denoted by the radical symbol (√). For example, the square root of 9 is written as √9, which equals 3 because 3 × 3 = 9. Every positive number has two square roots: a positive root and a negative root. However, we typically refer to the positive root when discussing square roots.
Here are some key points to understand about square roots:
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are whole numbers.
- Non-Perfect Squares: Numbers like 2, 3, 5, 7, and 80 are non-perfect squares because their square roots are not whole numbers and are often expressed in simplified radical form.
- Prime Factorization: Breaking down a number into its prime factors can help simplify square roots, especially for non-perfect squares.
- Simplifying Square Roots: The process involves expressing the number under the radical as a product of its prime factors and then simplifying by taking out pairs of factors.
In the next sections, we will delve deeper into the methods and steps to simplify the square root of 80, making it easy to understand and apply.
Understanding the Square Root of 80
The square root of 80, represented as \( \sqrt{80} \), is a value that, when multiplied by itself, equals 80. To understand how to simplify \( \sqrt{80} \), we need to break it down into its prime factors and identify perfect squares.
First, let's express 80 as a product of its prime factors:
- 80 = 2 × 2 × 2 × 2 × 5
We can group the prime factors to identify the perfect squares:
- 80 = (2 × 2) × (2 × 2) × 5 = 4 × 4 × 5
Next, we take the square root of each group:
- \( \sqrt{80} = \sqrt{(4 \times 4 \times 5)} = \sqrt{4} \times \sqrt{4} \times \sqrt{5} = 2 \times 2 \times \sqrt{5} = 4\sqrt{5} \)
Thus, the simplified form of the square root of 80 is:
- \( \sqrt{80} = 4\sqrt{5} \)
This means that \( \sqrt{80} \) in its simplest radical form is \( 4\sqrt{5} \). In decimal form, this is approximately 8.944.
Understanding the simplification process helps in various mathematical applications, making it easier to work with square roots in equations and other calculations.
Prime Factorization Method
The prime factorization method is a systematic way to simplify the square root of a number by breaking it down into its prime factors. Here, we will use this method to simplify the square root of 80.
- Find the Prime Factors of 80:
First, we need to express 80 as a product of its prime factors. The prime factorization of 80 is:
80 = 2 × 2 × 2 × 2 × 5
- Group the Prime Factors:
Next, we group the prime factors into pairs of identical factors:
80 = (2 × 2) × (2 × 2) × 5
- Rewrite the Expression Using Square Roots:
We can rewrite the expression to separate the pairs and the remaining factor:
\(\sqrt{80} = \sqrt{(2^2) \times (2^2) \times 5}\)
- Take the Square Roots of the Pairs:
Since the square root of a squared number is the number itself, we simplify each pair:
\(\sqrt{(2^2)} = 2\)
So, we have:
\(\sqrt{80} = 2 \times 2 \times \sqrt{5}\)
- Simplify the Expression:
Multiplying the constants gives us the simplified form:
\(\sqrt{80} = 4\sqrt{5}\)
Therefore, the square root of 80 simplified using the prime factorization method is \(4\sqrt{5}\).
Step-by-Step Simplification Process
Simplifying the square root of 80 involves a few clear steps. Let's break it down:
-
Prime Factorization: Begin by finding the prime factors of 80.
80 can be factored into \(2 \times 2 \times 2 \times 2 \times 5\).
-
Pair the Factors: Identify pairs of prime factors.
\(80 = 2^4 \times 5\) which can be written as \((2^2) \times (2^2) \times 5\).
-
Apply the Square Root: Apply the square root to each pair.
\(\sqrt{80} = \sqrt{(2^2) \times (2^2) \times 5}\)
\(\sqrt{(2^2)} = 2\), so we have two pairs of 2's:
\(\sqrt{80} = 2 \times 2 \times \sqrt{5}\)
-
Simplify: Combine the simplified factors.
\(2 \times 2 = 4\), so:
\(\sqrt{80} = 4\sqrt{5}\)
Therefore, the simplified form of the square root of 80 is \(4\sqrt{5}\).

Breaking Down the Radicals
Breaking down radicals involves simplifying the expression under the radical sign to its prime factors and then simplifying further where possible. Let’s break down the square root of 80 step-by-step.
- First, identify the prime factors of 80. The prime factorization of 80 is:
- 80 = 2 × 2 × 2 × 2 × 5
- Group the prime factors into pairs of equal factors:
- 80 = (2 × 2) × (2 × 2) × 5 = 4 × 4 × 5
- Rewrite the expression using the square root properties:
- \(\sqrt{80} = \sqrt{(2 \times 2) \times (2 \times 2) \times 5}\)
- \(\sqrt{80} = \sqrt{4 \times 4 \times 5}\)
- Take the square root of the perfect squares (4 in this case):
- \(\sqrt{80} = \sqrt{4} \times \sqrt{4} \times \sqrt{5}\)
- \(\sqrt{80} = 2 \times 2 \times \sqrt{5}\)
- Combine the simplified factors:
- \(\sqrt{80} = 4\sqrt{5}\)
Thus, the square root of 80 simplified is \(4\sqrt{5}\). This process of breaking down the radicals allows us to express the square root in its simplest radical form, making it easier to work with in various mathematical applications.
Combining the Simplified Factors
After breaking down the square root of 80 into its prime factors and simplifying the radicals, we combine the simplified factors to get the final simplified form.
We start with the square root of 80:
\[\sqrt{80}\]
First, we perform prime factorization on 80:
\[80 = 2 \times 2 \times 2 \times 2 \times 5 = 2^4 \times 5\]
Next, we group the factors in pairs of squares:
\[80 = (2^2 \times 2^2) \times 5\]
Now, we take the square root of each group:
\[\sqrt{80} = \sqrt{(2^2 \times 2^2) \times 5} = \sqrt{2^2} \times \sqrt{2^2} \times \sqrt{5} = 2 \times 2 \times \sqrt{5} = 4\sqrt{5}\]
Thus, the simplified form of the square root of 80 is:
\[\sqrt{80} = 4\sqrt{5}\]
This process demonstrates how we combine the simplified factors to express the square root of 80 in its simplest radical form. By factoring out the perfect squares and simplifying, we achieve the final result of \(4\sqrt{5}\).
Verifying the Simplified Form
To verify that our simplification of the square root of 80 is correct, we need to ensure that the expression 4√5 is equivalent to the original √80.
-
Calculate the square root of the simplified form:
The simplified form we obtained is 4√5. First, let's compute the square of this expression:
\[(4\sqrt{5})^2 = 4^2 \times (\sqrt{5})^2 = 16 \times 5 = 80\]
-
Compare it to the original value:
We see that squaring 4√5 returns the original value of 80, verifying that the simplification is indeed correct.
-
Verify using decimal approximation:
We know that:
\[\sqrt{80} \approx 8.94427191\]
And, calculating the decimal form of 4√5:
\[4 \times \sqrt{5} \approx 4 \times 2.236 = 8.944\]
The decimal values match, providing further verification of our simplification.
Thus, through both exact and decimal verification, we confirm that the simplified form 4√5 is accurate for the square root of 80.
Practical Applications of Simplifying Square Roots
The process of simplifying square roots, such as finding the simplest form of the square root of 80, has numerous practical applications across various fields. Here are some key examples:
- Mathematics and Engineering: Simplified square roots are essential in solving equations and optimizing calculations. For instance, in engineering, they are used to determine natural frequencies of structures like bridges, aiding in predicting how they will respond to loads.
- Science: Square roots are frequently used in scientific calculations, such as determining velocities, calculating the amount of radiation absorbed by materials, and analyzing sound wave intensities. These calculations help scientists develop new technologies and understand natural phenomena.
- Statistics: In statistical analysis, square roots are used to calculate standard deviation, which measures how much data varies from the mean. This is crucial for interpreting data and making informed decisions.
- Architecture: Architects use simplified square roots to accurately calculate areas and volumes of spaces. This helps in creating precise models and structures, ensuring stability and efficiency in designs.
- Finance: Square roots are used to assess stock market volatility, which is crucial for evaluating investment risks. This involves calculating the variance of stock returns and then taking the square root to understand the level of fluctuation.
- Computer Science: In programming, simplified expressions involving square roots are used to enhance computational efficiency. They play a role in encryption algorithms, image processing, and game development.
- Navigation: Pilots and navigators use square roots to calculate distances between points on maps, helping in plotting accurate courses and estimating travel times.
- Accident Investigations: Police officers use square roots to determine the speed of vehicles based on skid mark measurements. This helps in reconstructing accidents and understanding vehicle dynamics before a crash.
The ability to simplify square roots thus plays a pivotal role in various academic and professional disciplines, making mathematical processes more efficient and applications more precise.
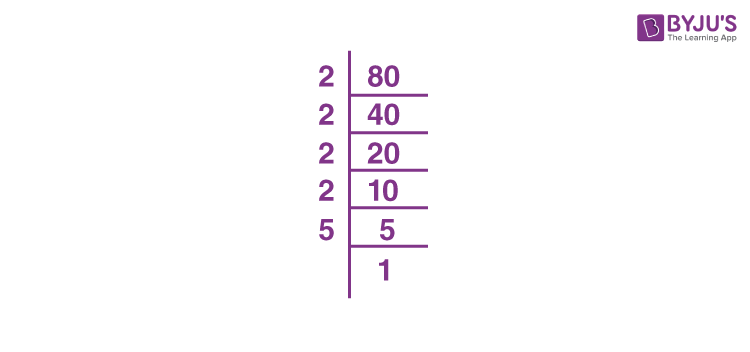
Common Mistakes to Avoid
When simplifying square roots, such as the square root of 80, several common mistakes can hinder the process. Here are some key errors to watch out for:
- Overlooking Prime Factorization: Skipping the step of breaking down the number into its prime factors can lead to incomplete or incorrect simplification. Always start by finding the prime factors.
- Ignoring Square Factors: Failing to correctly identify and extract square factors can result in a simplified form that is not fully reduced. Ensure you identify all possible square factors.
- Miscalculating Square Roots: Incorrectly calculating the square roots of factors, especially larger numbers, can derail the entire simplification process. Double-check your calculations for accuracy.
- Mixing Radicands: Combining or simplifying different radicands without proper methods can lead to inaccuracies. Each square root should be simplified individually unless they can be combined under the same radicand.
- Confusing Multiplication and Addition: Misapplying the properties of square roots, such as assuming \( \sqrt{a} + \sqrt{b} = \sqrt{a+b} \), which is incorrect, can lead to significant errors. Remember that square roots should be simplified according to multiplication, not addition.
By recognizing and avoiding these common mistakes, you can improve your proficiency in simplifying square roots and achieve more accurate results.
Advanced Simplification Techniques
To further simplify square roots, like the square root of 80, several advanced techniques can be applied. These methods not only streamline the process but also enhance accuracy and understanding.
1. Prime Factorization
Prime factorization involves breaking down a number into its prime factors. For example, for \(\sqrt{80}\), we have:
\(\sqrt{80} = \sqrt{2^4 \times 5} = \sqrt{2^4} \times \sqrt{5} = 4\sqrt{5}\)
2. Radical Simplification Calculators
Using online calculators or software tools that specialize in mathematical operations can simplify square roots quickly and accurately.
3. Algebraic Identities
Applying algebraic identities can help simplify complex square roots. For instance:
- Using \((a \cdot b)^2 = a^2 \cdot b^2\) to separate terms under the square root.
- Simplifying expressions like \(\sqrt{a^2 \cdot b} = a\sqrt{b}\).
4. Rationalizing the Denominator
When dealing with fractions, rationalizing the denominator can simplify the expression. For example:
\(\frac{1}{\sqrt{80}} = \frac{1}{4\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{20}\)
5. Graphical Representation
Visual aids, such as graphs, can illustrate the relationships between values, making it easier to understand the concept of square roots and their simplifications.
6. Mathematical Software
Programs like Mathematica, MATLAB, or Python libraries (e.g., NumPy) offer advanced functions for simplifying square roots and conducting precise mathematical computations.
Example Problem
Let's simplify \(\sqrt{200}\) using these techniques:
\(\sqrt{200} = \sqrt{2^3 \times 5^2} = \sqrt{4 \times 5^2} \times \sqrt{2} = 10\sqrt{2}\)
By employing these advanced techniques, the simplification of square roots becomes a more accessible and efficient process, opening up a world of possibilities for applying these concepts in various mathematical contexts.
Hướng dẫn đơn giản hóa căn bậc hai của 80 bằng cách sử dụng phương pháp phân tích số nguyên tố. Phù hợp cho những ai muốn tìm hiểu toán học cơ bản.
Cách Đơn Giản Hóa Căn Bậc Hai Của 80: sqrt(80)
READ MORE:
Hướng dẫn cách đơn giản hóa căn bậc hai của một số bằng cách sử dụng cây nhân tố. Ví dụ minh họa với căn bậc hai của 80.
Đơn Giản Hóa Căn Bậc Hai Của Một Số Bằng Cây Nhân Tố, Sqrt(80)











