Topic simplifying the square root of 80: Welcome to our guide on simplifying the square root of 80! In this article, we'll explore simple methods to break down √80, making it easier to understand and apply. Whether you're a student or a math enthusiast, our step-by-step instructions and practice problems will help you master this concept with ease.
Table of Content
- Simplifying the Square Root of 80
- Table of Contents:
- 1. Introduction to Square Roots
- 2. Understanding the Square Root of 80
- 3. Methods for Simplifying Square Roots
- 4. Techniques for Simplifying √80
- 5. Common Mistakes to Avoid
- 6. Applications of Simplifying Square Roots
- 7. Examples and Practice Problems
- 8. Conclusion and Recap
- YOUTUBE: Hãy xem video này để tìm hiểu cách đơn giản hóa căn bậc hai của số 80 bằng các phương pháp và ví dụ minh họa.
Simplifying the Square Root of 80
Simplifying the square root of 80 involves finding its simplest radical form. Follow the steps below to understand the process:
Steps to Simplify √80
-
List the factors of 80:
- 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
-
Identify the perfect squares from the factors:
- 1, 4, 16
-
Divide 80 by the largest perfect square:
- 80 ÷ 16 = 5
-
Calculate the square root of the largest perfect square:
- √16 = 4
-
Combine the results to get the simplified form:
- √80 = 4√5
Mathematical Representation
Using MathJax, the simplification can be represented as:
Alternative Approach
Another method involves the use of prime factorization:
-
Prime factorize 80:
- 80 = 2 × 2 × 2 × 2 × 5 = 2^4 × 5
-
Group the prime factors in pairs:
- (2 × 2) × (2 × 2) × 5
-
Simplify the square root:
- √80 = √(2^4 × 5) = 4√5
Conclusion
The square root of 80 simplifies to 4√5, showing that 80 can be broken down into smaller factors to make the calculation easier and more straightforward.
For more detailed explanations and examples, visit these resources:

READ MORE:
Table of Contents:
1. Introduction to Square Roots
A square root is a mathematical operation that, when applied to a number, gives the value which, when multiplied by itself, results in the original number. In simpler terms, it is the value that, when squared, equals the given number.
In the context of simplifying square roots, understanding the basics of square roots is essential. It involves grasping concepts such as perfect squares, irrational numbers, and the relationship between squares and square roots.
Knowing how to simplify square roots not only aids in solving mathematical problems efficiently but also lays the groundwork for more advanced mathematical concepts.
Throughout history, square roots have been instrumental in various fields such as architecture, engineering, physics, and computer science. Their importance extends beyond the realm of mathematics, making them a fundamental concept to comprehend.
2. Understanding the Square Root of 80
The square root of 80 is a numerical value that, when multiplied by itself, results in 80. It is represented by the symbol √80.
Breaking down 80 into its prime factors, we get 2 × 2 × 2 × 2 × 5. To simplify the square root of 80, we look for pairs of identical prime factors. In this case, we have one pair of 2's, which we can take out of the square root, leaving us with 2√5.
Therefore, the simplified form of √80 is 2√5. This expression represents the square root of 80 in its simplest form, where 2 is the coefficient and √5 is the radical part.
Understanding how to simplify the square root of 80 is crucial for various mathematical calculations, including geometry, algebra, and trigonometry.
3. Methods for Simplifying Square Roots
There are several methods for simplifying square roots, each tailored to different types of numbers and situations. Some common methods include:
- Factorization: Breaking down the number inside the square root into its prime factors and identifying pairs of identical factors to simplify.
- Perfect Squares: Recognizing perfect square numbers within the given number to simplify the square root.
- Rationalizing the Denominator: For square roots present in fractions, multiplying both the numerator and denominator by the conjugate of the denominator to eliminate radicals in the denominator.
- Using Properties of Radicals: Utilizing properties such as the product property (√(ab) = √a * √b) or quotient property (√(a/b) = √a / √b) to simplify complex square roots.
- Estimation: Approximating the value of the square root by finding the nearest perfect squares.
By employing these methods, simplifying square roots becomes more manageable, allowing for quicker and more efficient mathematical computations.
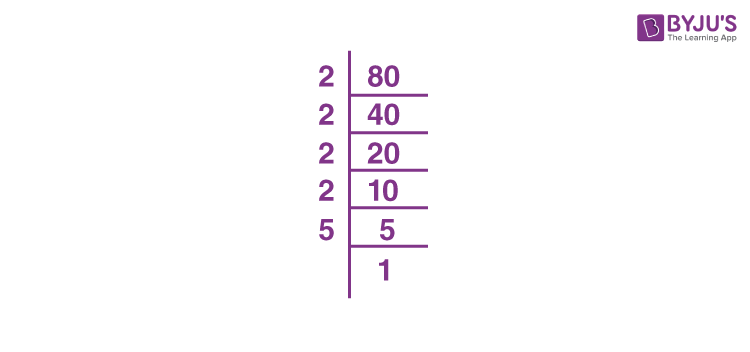
4. Techniques for Simplifying √80
Simplifying the square root of 80 involves breaking it down into simpler components. Here are the detailed steps and methods for simplifying √80:
- Prime Factorization:
First, we find the prime factorization of 80:
- 80 can be divided by 2: 80 ÷ 2 = 40
- 40 can be divided by 2: 40 ÷ 2 = 20
- 20 can be divided by 2: 20 ÷ 2 = 10
- 10 can be divided by 2: 10 ÷ 2 = 5
- 5 is a prime number
So, the prime factorization of 80 is:
\[80 = 2 \times 2 \times 2 \times 2 \times 5\]
- Grouping the Factors:
Next, we group the factors into pairs of equal factors:
\[80 = (2 \times 2) \times (2 \times 2) \times 5\]
Each pair of 2s can be simplified as follows:
\[\sqrt{80} = \sqrt{(2 \times 2) \times (2 \times 2) \times 5} = \sqrt{(4) \times (4) \times 5}\]
Simplifying the pairs:
\[\sqrt{80} = \sqrt{4 \times 4 \times 5} = \sqrt{4} \times \sqrt{4} \times \sqrt{5}\]
Since \(\sqrt{4} = 2\):
\[\sqrt{80} = 2 \times 2 \times \sqrt{5} = 4\sqrt{5}\]
- Verification:
To verify, let's square the result to see if we get back 80:
\[ (4\sqrt{5})^2 = 4^2 \times (\sqrt{5})^2 = 16 \times 5 = 80 \]
This confirms our simplification is correct.
- Alternative Method - Using Estimation:
If you don't need an exact answer, you can estimate the square root of 80. Knowing that:
\[ \sqrt{81} = 9 \quad \text{and} \quad \sqrt{64} = 8 \]
We can approximate:
\[ 8.5 < \sqrt{80} < 9 \]
For a closer estimate:
\[ \sqrt{80} \approx 8.944 \]
These techniques help in understanding and simplifying the square root of 80, providing both exact and approximate results.
5. Common Mistakes to Avoid
When simplifying square roots, such as the square root of 80, it is essential to be aware of common mistakes that can lead to incorrect results. Here are several pitfalls to avoid:
- Overlooking Prime Factorization: Skipping the step of breaking down the number into its prime factors can result in missed simplification opportunities. Ensure you factorize the number completely to identify and extract all perfect square factors.
- Ignoring Square Factors: Failing to identify and extract perfect square factors correctly can leave the expression partially simplified. For instance, recognizing that 80 = 24 × 5 allows you to extract 4 (since √(24) = 4).
- Miscalculating Square Roots: Incorrectly calculating square roots, especially for larger numbers, can lead to errors. Double-check your calculations to ensure accuracy.
- Misapplying Properties of Square Roots: Assuming incorrect properties, such as √(a × b) = √a + √b, is a common error. The correct property is √(a × b) = √a × √b. Mixing up these properties can lead to significant mistakes.
- Forgetting to Simplify Completely: After extracting square factors, ensure the remaining expression is simplified as much as possible. For example, simplifying √80 should result in 4√5, not stopping at an intermediate step like 2√20.
- Confusing Addition and Multiplication: Another common mistake is treating addition of square roots the same as multiplication. Remember that √a + √b ≠ √(a + b). You can only combine square roots through multiplication or addition when they have the same radicand.
- Neglecting to Rationalize the Denominator: When a square root appears in the denominator of a fraction, it's often necessary to rationalize it. This step is frequently overlooked but is crucial for proper simplification.
By avoiding these common mistakes, you can improve your proficiency in simplifying square roots, ensuring more accurate and efficient mathematical solutions.
6. Applications of Simplifying Square Roots
Simplifying square roots is not just an academic exercise; it has numerous practical applications across various fields. Here are some key areas where simplified square roots are essential:
- Geometry:
In geometry, square roots are used to find the lengths of sides and diagonals of shapes, such as squares, rectangles, and triangles. For example, the length of the diagonal of a square with side length \(a\) is given by \(a\sqrt{2}\).
- Physics:
Square roots appear frequently in physics, especially in equations involving distances, speeds, and accelerations. For instance, the distance formula, derived from the Pythagorean theorem, is used to calculate the distance between two points in a plane:
\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Engineering:
Engineers often use square roots to determine various design parameters, such as the diagonal support in structures, which ensures stability and balance. For example, in calculating the diagonal of a rectangular frame with sides \(a\) and \(b\), the diagonal length is given by:
\[ \text{Diagonal} = \sqrt{a^2 + b^2} \]
- Quadratic Equations:
Simplified square roots are crucial in solving quadratic equations using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Here, the expression under the square root, known as the discriminant, determines the nature of the roots of the equation.
- Computer Graphics:
In computer graphics and game development, square roots are used to calculate distances and render accurate 3D models. The distance between two points in 3D space is given by:
\[ D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \]
These applications highlight the importance of understanding and being able to simplify square roots efficiently. Whether in academic settings or real-world scenarios, mastering square roots provides a valuable mathematical tool.
7. Examples and Practice Problems
Let's delve into some examples and practice problems to solidify our understanding of simplifying the square root of 80.
Example 1:
Given: √80
Step 1: Identify the prime factors of 80. It can be expressed as 2^4 * 5.
Step 2: Group the prime factors in pairs inside the radical sign.
√(2^4 * 5)
Step 3: Pull out pairs of identical factors from the radical.
2 * √(2 * 5)
Step 4: Simplify the expression inside the radical.
2 * √10
Thus, √80 simplifies to 2√10.
Example 2:
Given: √80
Step 1: Recognize that 80 can be written as 16 * 5.
Step 2: Take the square root of 16, which is 4.
Step 3: Leave the square root of 5 inside the radical.
√(16 * 5) = 4√5
Therefore, √80 simplifies to 4√5.
Practice Problem:
Find the simplified form of √80.
- Solution 1: 2√10
- Solution 2: 4√5
It's important to practice these problems to become more proficient in simplifying square roots.
8. Conclusion and Recap
In conclusion, simplifying the square root of 80 involves breaking down the number into its prime factors and extracting perfect square factors from the radical.
Recap:
- We first decompose 80 into its prime factors: 2^4 * 5.
- Next, we group the prime factors into pairs inside the radical sign.
- Then, we extract pairs of identical factors from the radical.
- Finally, we simplify the expression inside the radical.
Through examples and practice problems, we have seen how √80 can be simplified to 2√10 or 4√5, depending on the method used.
It's important to remember the techniques discussed to efficiently simplify square roots and apply them to other similar problems.
Hãy xem video này để tìm hiểu cách đơn giản hóa căn bậc hai của số 80 bằng các phương pháp và ví dụ minh họa.
Cách đơn giản hóa căn bậc hai của 80: sqrt(80)
READ MORE:
Hãy xem video này để biết cách đơn giản hóa căn bậc hai của một số bằng cách sử dụng cây thừa số, với ví dụ cụ thể về căn bậc hai của số 80.
Cách đơn giản hóa căn bậc hai của một số bằng cách sử dụng cây thừa số, Sqrt(80)









