Topic simplifying radicals square roots: Unlock the secrets of simplifying radicals and square roots with our comprehensive guide. Whether you're a student or a math enthusiast, mastering these techniques will boost your algebra skills and confidence. Dive into step-by-step methods, practical examples, and expert tips to make simplifying radicals and square roots a breeze.
Table of Content
- Understanding and Simplifying Radicals and Square Roots
- Introduction to Radicals and Square Roots
- Basic Definitions and Concepts
- Simplifying Square Roots: Step-by-Step Guide
- Simplifying Higher-Order Roots
- Prime Factorization Method
- Pairing Factors to Simplify Radicals
- Special Cases in Simplifying Radicals
- Rationalizing the Denominator
- Examples and Practice Problems
- Common Mistakes to Avoid
- Applications of Simplified Radicals in Algebra
- Advanced Techniques and Tips
- Conclusion and Summary
- Additional Resources and Further Reading
- YOUTUBE:
Understanding and Simplifying Radicals and Square Roots
Radicals and square roots are fundamental concepts in algebra that involve expressing numbers in a specific form. Simplifying these expressions helps in solving equations and understanding mathematical relationships.
Basic Concepts
A radical expression involves a root, such as a square root, cube root, or higher roots. The square root of a number \(x\) is a number \(y\) such that \(y^2 = x\).
- Square Root: \( \sqrt{x} \)
- Cube Root: \( \sqrt[3]{x} \)
- n-th Root: \( \sqrt[n]{x} \)
Properties of Radicals
Understanding the properties of radicals is essential for simplifying them:
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \(\sqrt{a^2} = |a|\)
Steps to Simplify Radicals
To simplify a radical expression, follow these steps:
- Factor the number inside the radical: Break down the number into its prime factors.
- Pair the factors: For square roots, pair the prime factors. For cube roots, group them in triples, and so on.
- Move pairs outside the radical: Each pair of factors comes out of the radical as a single number.
Examples
Let's look at some examples to illustrate the simplification process:
- \(\sqrt{18}\):
- Factor 18: \(18 = 2 \times 3^2\)
- Pair the factors: \(2 \times (3 \times 3)\)
- Move pairs outside the radical: \(3\sqrt{2}\)
- \(\sqrt{50}\):
- Factor 50: \(50 = 2 \times 5^2\)
- Pair the factors: \(2 \times (5 \times 5)\)
- Move pairs outside the radical: \(5\sqrt{2}\)
Special Cases
There are some special cases to be aware of when simplifying radicals:
- When the radicand is a perfect square, such as \(\sqrt{25}\), it simplifies to an integer (in this case, 5).
- Radicals can sometimes be simplified by rationalizing the denominator, for example, \(\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\).
Practice Problems
Try simplifying these radicals on your own:
- \(\sqrt{72}\)
- \(\sqrt{200}\)
- \(\sqrt[3]{54}\)

READ MORE:
Introduction to Radicals and Square Roots
Radicals and square roots are fundamental concepts in mathematics, particularly in algebra. Understanding these concepts is crucial for solving various types of equations and for simplifying expressions. This section will introduce you to the basic idea of radicals and square roots, their properties, and their significance in mathematics.
Definition:
A radical is an expression that includes a root symbol (√). The most common type of radical is the square root, but there are also cube roots, fourth roots, and higher-order roots. The general form of a radical is written as:
\(\sqrt[n]{x}\)
where \(n\) is the index of the radical, and \(x\) is the radicand.
Square Root:
The square root is the most frequently encountered radical. It is the value that, when multiplied by itself, gives the original number. The square root of \(x\) is written as:
\(\sqrt{x}\)
For example:
- \(\sqrt{9} = 3\), because \(3 \times 3 = 9\)
- \(\sqrt{16} = 4\), because \(4 \times 4 = 16\)
Properties of Radicals:
Understanding the properties of radicals is essential for simplifying them. Some key properties include:
- Product Property: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Power Property: \(\sqrt[n]{a^m} = a^{\frac{m}{n}}\)
Why Learn About Radicals and Square Roots?
Radicals and square roots are used in various fields such as engineering, physics, and computer science. They are essential for solving quadratic equations, working with geometric shapes, and understanding scientific measurements.
By mastering radicals and square roots, you'll be able to simplify complex mathematical expressions and solve a wide range of problems more efficiently.
Basic Definitions and Concepts
Understanding the basics of radicals and square roots is essential for simplifying these expressions. Here are some fundamental definitions and concepts to get started:
- Radical: A radical expression includes a root symbol (√) with an expression underneath. It represents the root of a number.
- Square Root: The square root of a number a is a number b such that \(b^2 = a\). It is denoted as \(\sqrt{a}\).
- Radicand: The number or expression inside the radical symbol. For \(\sqrt{a}\), a is the radicand.
- Index: The small number written just outside and to the left of the radical sign, indicating the degree of the root. The default index is 2 for square roots.
Here are some important properties and concepts related to radicals:
- Product Property: The square root of a product is equal to the product of the square roots of the factors: \[ \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \]
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
- Power of a Radical: A radical expression can be written with fractional exponents. For example: \[ \sqrt{a} = a^{\frac{1}{2}} \]
These properties help simplify and manipulate radical expressions effectively. Understanding and applying them is crucial for further exploration and simplification of radicals and square roots.
Simplifying Square Roots: Step-by-Step Guide
Simplifying square roots involves breaking down the number under the radical sign into its prime factors and then simplifying it using the properties of square roots. Follow these detailed steps to simplify square roots:
-
Identify Perfect Square Factors:
Find the largest perfect square factor of the number under the radical. A perfect square is a number like 1, 4, 9, 16, etc., which are squares of integers (1, 2, 3, 4, etc.).
-
Rewrite the Radicand:
Express the number under the radical as a product of its perfect square factor and another number.
For example, to simplify \( \sqrt{72} \):
- List the factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72.
- Identify the largest perfect square factor: 36.
- Rewrite: \( 72 = 36 \times 2 \).
-
Separate and Simplify:
Use the property \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \) to separate the square root into two parts.
Continuing with \( \sqrt{72} \):
- \( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} \).
- Simplify: \( \sqrt{36} = 6 \), so \( \sqrt{72} = 6 \times \sqrt{2} \).
Let's look at another example for clarity:
Example: Simplify \( \sqrt{50} \)
- Identify perfect square factors: The factors of 50 are 1, 2, 5, 10, 25, 50. The largest perfect square factor is 25.
- Rewrite: \( 50 = 25 \times 2 \).
- Separate and simplify: \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5 \times \sqrt{2} \).
Therefore, \( \sqrt{50} = 5\sqrt{2} \).
By following these steps, you can simplify any square root. Practice with various examples to become proficient in this method. Remember, the key is to find the largest perfect square factor and then use the properties of square roots to simplify.
Simplifying Higher-Order Roots
Higher-order roots involve roots beyond the square root, such as cube roots (∛) and fourth roots (∜). Simplifying these radicals follows a similar process to simplifying square roots but with some additional considerations.
Step-by-Step Guide to Simplifying Higher-Order Roots
-
Identify the Index and the Radicand: The index is the small number outside the radical sign that indicates the degree of the root. The radicand is the number inside the radical. For example, in ∛27, the index is 3, and the radicand is 27.
-
Factor the Radicand: Break down the radicand into its prime factors. This helps in identifying groups that match the index of the root.
- Example: To simplify ∜16, factor 16 into its prime factors: \(16 = 2^4\).
-
Group Factors According to the Index: Group the prime factors into sets that match the index of the root. Each group can be taken out of the radical.
- Example: For ∜16, since the index is 4, group the factors into sets of 4: \(2^4\).
- Take one factor out for each complete group: ∜16 = 2.
-
Multiply the Results Outside the Radical: If there are multiple groups, multiply the results outside the radical.
- Example: ∛(8 * 27) = ∛8 * ∛27 = 2 * 3 = 6.
-
Combine Like Terms: If simplifying results in terms that can be combined, do so to simplify the expression further.
Examples
Here are a few examples to illustrate the process:
-
Example 1: Simplify ∛(64).
- Factor 64: \(64 = 2^6\).
- Group the factors by the index (3): \(2^6 = (2^3) \cdot (2^3)\).
- Take one factor out of each group: ∛64 = 2 * 2 = 4.
-
Example 2: Simplify ∜(81x^8).
- Factor 81 and \(x^8\): \(81 = 3^4\) and \(x^8 = (x^2)^4\).
- Group the factors by the index (4): \(\left(3^4\right) \cdot \left((x^2)^4\right)\).
- Take one factor out of each group: ∜(81x^8) = 3 * \(x^2\) = 3\(x^2\).
Key Properties
When working with higher-order roots, keep these properties in mind:
- \(\sqrt[n]{a \cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b}\): The product of roots is the root of the product.
- \(\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}\): The quotient of roots is the root of the quotient.
- \(\sqrt[n]{a^m} = a^{\frac{m}{n}}\): A root can be expressed as a fractional exponent.

Prime Factorization Method
The prime factorization method is a systematic approach to simplify radicals by breaking down the radicand (the number under the radical sign) into its prime factors. Here are the detailed steps to simplify radicals using the prime factorization method:
-
Find the Prime Factorization: Start by finding the prime factors of the radicand. Prime factors are the prime numbers that multiply together to give the original number.
- For example, to simplify
\\(\sqrt{72}\\) , start by finding the prime factorization of 72. - The prime factorization of 72 is
\\(72 = 2 \times 2 \times 2 \times 3 \times 3\\) .
- For example, to simplify
-
Group the Factors: Group the prime factors in pairs for square roots, triples for cube roots, and so on, depending on the index of the root.
- In our example, group the factors of 72:
\\(72 = (2 \times 2) \times (3 \times 3) \times 2\\) .
- In our example, group the factors of 72:
-
Simplify by Taking Out Pairs: For each pair of factors, take one factor out of the radical.
- From
\\(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2}\\) , take out one 2 and one 3:\\(\sqrt{72} = 2 \times 3 \times \sqrt{2}\\) .
- From
-
Write the Simplified Radical: Multiply the factors outside the radical and leave the remaining factors inside.
- The simplified form of
\\(\sqrt{72}\\) is\\(6\sqrt{2}\\) .
- The simplified form of
Let's see another example to reinforce the concept:
Example: Simplify
- Prime factorization of 180:
\\(180 = 2 \times 2 \times 3 \times 3 \times 5\\) - Group the factors:
\\((2 \times 2) \times (3 \times 3) \times 5\\) - Simplify by taking out pairs:
\\(\sqrt{180} = \sqrt{(2 \times 2) \times (3 \times 3) \times 5} = 2 \times 3 \times \sqrt{5}\\) - Simplified form:
\\(\sqrt{180} = 6\sqrt{5}\\)
By using the prime factorization method, you can systematically simplify any radical expression. This method is particularly useful for higher-order roots and for understanding the structure of the numbers involved.
Pairing Factors to Simplify Radicals
When simplifying radicals, pairing factors is a crucial step. This method helps to reduce the radical to its simplest form. Here are the detailed steps to follow:
- Factor the Radicand:
Start by factoring the number under the radical (the radicand) into its prime factors. For example, if the radicand is 72, we factor it as follows:
\(72 = 2 \times 2 \times 2 \times 3 \times 3\)
- Pair the Factors:
Group the prime factors into pairs. Each pair of the same number can be simplified to a single factor outside the radical. For instance, in the factorization of 72:
\(72 = (2 \times 2) \times (3 \times 3) \times 2\)
- Move Pairs Outside the Radical:
For each pair of factors, take one factor out of the radical. Any unpaired factors remain inside the radical. Continuing with our example:
\(\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
This method can be applied to both square roots and higher-order roots. Here are some additional examples:
- Simplifying \(\sqrt{50}\):
Factorize: \(50 = 2 \times 5 \times 5\)
Pair the factors: \(50 = 2 \times (5 \times 5)\)
Move pairs outside the radical: \(\sqrt{50} = 5\sqrt{2}\)
- Simplifying \(\sqrt[3]{54}\):
Factorize: \(54 = 2 \times 3 \times 3 \times 3\)
Group the factors into triplets for cube root: \(54 = 2 \times (3 \times 3 \times 3)\)
Move triplets outside the radical: \(\sqrt[3]{54} = 3\sqrt[3]{2}\)
By following these steps, you can simplify radicals efficiently and accurately. Practice with different numbers to become more comfortable with the process.
Special Cases in Simplifying Radicals
Simplifying radicals can sometimes involve special cases that require careful attention to ensure accuracy. These special cases often arise due to unique properties of numbers and radicals. Here, we will explore some of these special cases and provide steps to handle them.
1. Simplifying Radicals with Negative Numbers
When dealing with square roots of negative numbers, the result involves imaginary numbers. The imaginary unit is denoted as \(i\), where \(i = \sqrt{-1}\). For example:
- \(\sqrt{-9} = \sqrt{-1 \times 9} = \sqrt{-1} \times \sqrt{9} = i \times 3 = 3i\)
2. Simplifying Radicals with Even and Odd Powers
For higher-order roots, such as cube roots or fourth roots, the simplification depends on whether the exponent is even or odd:
- Even Powers: When simplifying even powers under a radical, the result must account for the absolute value to ensure non-negativity. For example, \(\sqrt[4]{x^4} = |x|\).
- Odd Powers: When simplifying odd powers, the result directly takes the value of the variable, as odd roots preserve the sign of the base. For example, \(\sqrt[3]{x^3} = x\).
3. Simplifying Radicals with Fractions
When simplifying square roots that involve fractions, both the numerator and the denominator should be simplified separately:
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Example: \(\sqrt{\frac{49}{9}} = \frac{\sqrt{49}}{\sqrt{9}} = \frac{7}{3}\)
4. Simplifying Radicals with Non-Perfect Square Radicands
Sometimes the number inside the radical (the radicand) is not a perfect square. The goal is to factor the radicand into a product of perfect squares and other factors:
- Example: \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\)
5. Simplifying Higher-Order Radicals
For higher-order radicals, the approach involves factoring the radicand into perfect powers of the radical's degree:
- Example: \(\sqrt[3]{54} = \sqrt[3]{27 \times 2} = \sqrt[3]{27} \times \sqrt[3]{2} = 3\sqrt[3]{2}\)
6. Rationalizing the Denominator
Rationalizing the denominator involves removing radicals from the denominator of a fraction. This is done by multiplying both the numerator and the denominator by a suitable radical:
- Example: \(\frac{1}{\sqrt{3}} = \frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}\)
Rationalizing the Denominator
Rationalizing the denominator involves eliminating any radicals (square roots or higher-order roots) present in the denominator of a fraction. This process makes the expression easier to work with, especially in further calculations. Let's explore two common techniques for rationalizing the denominator: using a single term and using the conjugate.
Rationalizing with a Single Radical
When the denominator contains a single radical, we can eliminate it by multiplying both the numerator and the denominator by the same radical. This effectively removes the radical from the denominator.
- Identify the radical in the denominator.
- Multiply both the numerator and the denominator by the radical in the denominator.
- Simplify the resulting expression.
For example, consider the expression \( \frac{5}{\sqrt{3}} \):
\[
\frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}
\]
Here, we multiplied by \( \frac{\sqrt{3}}{\sqrt{3}} \), which is equal to 1, to eliminate the radical in the denominator.
Rationalizing with Conjugates
When the denominator is a binomial containing a radical, such as \( a + \sqrt{b} \), we use the conjugate to rationalize it. The conjugate of a binomial \( a + \sqrt{b} \) is \( a - \sqrt{b} \). Multiplying by the conjugate utilizes the difference of squares formula to eliminate the radical.
- Identify the binomial in the denominator and its conjugate.
- Multiply both the numerator and the denominator by the conjugate of the denominator.
- Expand and simplify the expression using the difference of squares formula.
For example, consider the expression \( \frac{2}{3 + \sqrt{5}} \):
\[
\frac{2}{3 + \sqrt{5}} \times \frac{3 - \sqrt{5}}{3 - \sqrt{5}} = \frac{2(3 - \sqrt{5})}{(3 + \sqrt{5})(3 - \sqrt{5})}
\]
Using the difference of squares formula \( (a + b)(a - b) = a^2 - b^2 \), we get:
\[
= \frac{6 - 2\sqrt{5}}{9 - 5} = \frac{6 - 2\sqrt{5}}{4} = \frac{3 - \sqrt{5}}{2}
\]
Special Cases
In cases involving higher-order radicals or more complex binomials, similar principles apply. For higher-order roots, multiply by a factor that converts the radicand to a perfect power. For example, to rationalize \( \frac{1}{\sqrt[3]{4}} \), multiply by \( \frac{\sqrt[3]{16}}{\sqrt[3]{16}} \) because \( \sqrt[3]{4} \times \sqrt[3]{16} = \sqrt[3]{64} = 4 \).
For expressions involving binomials with different terms like \( \sqrt{a} + \sqrt{b} \), use the respective conjugate to eliminate the radicals effectively.
Practice Problems
- Rationalize the denominator of \( \frac{7}{\sqrt{2}} \).
- Rationalize the denominator of \( \frac{5}{2 + \sqrt{3}} \).
- Rationalize the denominator of \( \frac{4}{\sqrt[3]{5}} \).
By practicing these techniques, you'll become proficient in simplifying expressions with radicals in the denominator.

Examples and Practice Problems
To solidify your understanding of simplifying radicals and square roots, let's go through some examples and practice problems. These will range from basic to more advanced problems involving single radicals, higher-order roots, and binomials with radicals.
Example 1: Simplifying Basic Square Roots
Simplify \( \sqrt{50} \).
- Identify the factors of 50 that include a perfect square: \[ \sqrt{50} = \sqrt{25 \times 2} \]
- Rewrite the square root as the product of the square root of the perfect square and the square root of the other factor: \[ \sqrt{50} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \]
Example 2: Simplifying Cube Roots
Simplify \( \sqrt[3]{54} \).
- Factor 54 into its prime factors: \[ 54 = 2 \times 3^3 \]
- Identify and extract the cube root of the perfect cube: \[ \sqrt[3]{54} = \sqrt[3]{2 \times 27} = \sqrt[3]{27} \times \sqrt[3]{2} = 3 \sqrt[3]{2} \]
Example 3: Simplifying Expressions with Multiple Radicals
Simplify \( \sqrt{72} + \sqrt{18} \).
- Factor each radicand into prime factors: \[ \sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2} \] \[ \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \]
- Combine like terms: \[ \sqrt{72} + \sqrt{18} = 6\sqrt{2} + 3\sqrt{2} = 9\sqrt{2} \]
Example 4: Rationalizing the Denominator
Simplify \( \frac{5}{2 + \sqrt{3}} \).
- Multiply the numerator and the denominator by the conjugate of the denominator: \[ \frac{5}{2 + \sqrt{3}} \times \frac{2 - \sqrt{3}}{2 - \sqrt{3}} \]
- Use the difference of squares formula to simplify the denominator: \[ = \frac{5(2 - \sqrt{3})}{(2 + \sqrt{3})(2 - \sqrt{3})} = \frac{10 - 5\sqrt{3}}{4 - 3} = \frac{10 - 5\sqrt{3}}{1} = 10 - 5\sqrt{3} \]
Example 5: Higher-Order Roots
Simplify \( \sqrt[4]{81x^8} \).
- Factor the radicand into perfect fourth powers: \[ \sqrt[4]{81x^8} = \sqrt[4]{3^4 \times (x^2)^4} \]
- Extract the fourth roots: \[ = 3 \times x^2 = 3x^2 \]
Practice Problems
Try solving these problems on your own to practice your skills:
- Simplify \( \sqrt{200} \).
- Simplify \( \sqrt[3]{125x^6} \).
- Simplify \( 4\sqrt{12} + 3\sqrt{27} \).
- Rationalize the denominator \( \frac{7}{\sqrt{5} - 2} \).
- Simplify \( \sqrt[5]{32a^{10}} \).
By working through these examples and problems, you'll gain a deeper understanding and greater confidence in simplifying radicals and square roots.
Common Mistakes to Avoid
When simplifying radicals and square roots, it's essential to be aware of common pitfalls that can lead to incorrect results. Here are some frequent mistakes and how to avoid them:
1. Incorrectly Combining Radicals
One of the most common mistakes is attempting to add or subtract radicals directly without proper simplification. Remember that you can only combine radicals with the same radicand.
For example, the expression \( \sqrt{2} + \sqrt{3} \) cannot be simplified to \( \sqrt{5} \) because the radicands are different. Instead, it remains as \( \sqrt{2} + \sqrt{3} \).
2. Improperly Simplifying Radicands
Sometimes, students forget to factor the radicand into its simplest form. Always look for perfect squares (or higher powers for higher-order roots) in the radicand to simplify.
For example, simplify \( \sqrt{50} \) as follows:
- Identify the perfect square factor: \( 50 = 25 \times 2 \).
- Simplify the radical: \[ \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \]
3. Misapplying the Product and Quotient Rules
The product and quotient rules for radicals are useful but can lead to errors if not applied correctly. The product rule states that \( \sqrt{a} \times \sqrt{b} = \sqrt{ab} \) and the quotient rule states that \( \frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \).
Be careful not to apply these rules to sums or differences under the radical. For example, \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \).
4. Failing to Rationalize the Denominator Properly
Rationalizing the denominator is crucial for simplifying expressions but can be tricky. Make sure to multiply by the appropriate form of 1 to eliminate the radical from the denominator.
For example, to simplify \( \frac{5}{\sqrt{2}} \):
- Multiply by \( \frac{\sqrt{2}}{\sqrt{2}} \): \[ \frac{5}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{5\sqrt{2}}{2} \]
In cases involving binomials, use the conjugate:
- To simplify \( \frac{3}{2 - \sqrt{5}} \), multiply by the conjugate \( \frac{2 + \sqrt{5}}{2 + \sqrt{5}} \): \[ \frac{3}{2 - \sqrt{5}} \times \frac{2 + \sqrt{5}}{2 + \sqrt{5}} = \frac{3(2 + \sqrt{5})}{4 - 5} = -3(2 + \sqrt{5}) = -6 - 3\sqrt{5} \]
5. Neglecting to Simplify Completely
After applying the steps to simplify a radical expression, always check if further simplification is possible. This includes combining like terms and reducing fractions.
For instance, after rationalizing the denominator of \( \frac{8}{2\sqrt{3}} \), you get:
\[
\frac{8}{2\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{8\sqrt{3}}{2 \times 3} = \frac{8\sqrt{3}}{6} = \frac{4\sqrt{3}}{3}
\]
6. Overlooking the Sign of the Radical
Radicals, especially square roots, should be considered in their principal (positive) form unless specified otherwise. Don't forget that the square root function typically returns the positive root.
For example, while \( x^2 = 4 \) has solutions \( x = 2 \) and \( x = -2 \), \( \sqrt{4} = 2 \) by definition.
Practice Problems to Avoid Common Mistakes
Try solving these practice problems while keeping in mind the common mistakes to avoid:
- Simplify \( \sqrt{72} + \sqrt{18} \).
- Rationalize the denominator \( \frac{3}{\sqrt{7} - 1} \).
- Simplify \( \frac{\sqrt{50}}{2} \).
- Combine \( 2\sqrt{5} + 3\sqrt{20} \).
- Simplify \( \sqrt[3]{27} + \sqrt[3]{8} \).
By avoiding these common mistakes, you can improve your accuracy and efficiency in working with radicals and square roots.
Applications of Simplified Radicals in Algebra
Simplifying radicals is not just an abstract mathematical exercise; it has practical applications in various areas of algebra and beyond. Understanding how to simplify radicals helps in solving equations, manipulating expressions, and analyzing real-world problems. Let's explore some key applications.
1. Solving Quadratic Equations
Quadratic equations often result in solutions involving square roots. Simplifying these radicals is crucial for finding and interpreting the solutions.
For example, consider the quadratic equation \( x^2 - 6x + 5 = 0 \). Solving using the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \) gives:
\[
x = \frac{6 \pm \sqrt{36 - 20}}{2} = \frac{6 \pm \sqrt{16}}{2} = \frac{6 \pm 4}{2}
\]
This simplifies to two solutions:
\[
x = \frac{6 + 4}{2} = 5 \quad \text{and} \quad x = \frac{6 - 4}{2} = 1
\]
2. Simplifying Algebraic Expressions
Simplified radicals make algebraic expressions easier to manipulate and understand. This is particularly useful in polynomial and rational expressions.
For instance, simplifying the expression \( \frac{\sqrt{50} + \sqrt{18}}{\sqrt{2}} \):
- Simplify the numerators: \[ \sqrt{50} = 5\sqrt{2}, \quad \sqrt{18} = 3\sqrt{2} \]
- Combine like terms: \[ \frac{5\sqrt{2} + 3\sqrt{2}}{\sqrt{2}} = \frac{8\sqrt{2}}{\sqrt{2}} \]
- Simplify the fraction: \[ = 8 \]
3. Rationalizing Denominators
In many algebraic contexts, it’s necessary to eliminate radicals from denominators to simplify expressions or prepare them for further operations.
Consider the expression \( \frac{3}{\sqrt{5} + 2} \). To rationalize the denominator, we multiply by the conjugate:
\[
\frac{3}{\sqrt{5} + 2} \times \frac{\sqrt{5} - 2}{\sqrt{5} - 2} = \frac{3(\sqrt{5} - 2)}{5 - 4} = 3(\sqrt{5} - 2)
\]
4. Solving Radical Equations
Equations involving radicals require simplification to solve. Simplified radicals help in isolating the variable and solving the equation.
For example, solve \( \sqrt{2x + 3} = 5 \):
- Square both sides to eliminate the square root: \[ (\sqrt{2x + 3})^2 = 5^2 \implies 2x + 3 = 25 \]
- Isolate the variable \( x \): \[ 2x = 22 \implies x = 11 \]
5. Geometry and Trigonometry
Radicals frequently appear in geometric formulas and trigonometric identities. Simplifying these radicals helps in calculating lengths, areas, and angles accurately.
For example, the length of the diagonal of a square with side length \( s \) is \( \sqrt{2} s \). In trigonometry, the sine and cosine of 45° are \( \frac{\sqrt{2}}{2} \), which are simplified radicals.
6. Analyzing Real-World Problems
Radicals appear in various real-world contexts, such as physics and engineering. Simplifying these expressions aids in solving problems involving distances, velocities, and other measurements.
For example, the distance \( d \) between two points \((x_1, y_1)\) and \((x_2, y_2)\) in a plane is given by:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
Simplifying the expression under the radical can make calculations more manageable.
Practice Problems
To apply these concepts, try solving the following problems:
- Solve the quadratic equation \( x^2 - 4x + 1 = 0 \) using the quadratic formula and simplify the result.
- Simplify the expression \( \frac{\sqrt{72} + \sqrt{18}}{3} \).
- Rationalize the denominator of \( \frac{5}{\sqrt{3} - 1} \).
- Solve the radical equation \( \sqrt{3x + 7} = x - 1 \).
- Calculate the length of the diagonal of a rectangle with side lengths \( 6 \) and \( 8 \).
Understanding and applying simplified radicals can enhance your problem-solving skills and provide deeper insights into algebraic and geometric concepts.
Advanced Techniques and Tips
Once you have mastered the basics of simplifying radicals and square roots, you can explore advanced techniques that can streamline the process and help you tackle more complex problems. Here are some advanced methods and tips to enhance your skills:
1. Simplifying Nested Radicals
Nested radicals involve radicals within radicals. Simplifying these requires recognizing patterns or using specific algebraic identities.
Consider the expression \( \sqrt{2 + \sqrt{3}} \). To simplify it:
- Assume \( \sqrt{2 + \sqrt{3}} = \sqrt{a} + \sqrt{b} \) for some integers \( a \) and \( b \).
- Square both sides: \[ 2 + \sqrt{3} = (\sqrt{a} + \sqrt{b})^2 = a + b + 2\sqrt{ab} \]
- Match the rational and irrational parts: \[ a + b = 2 \quad \text{and} \quad 2\sqrt{ab} = \sqrt{3} \]
- From \( 2\sqrt{ab} = \sqrt{3} \), solve \( ab = \frac{3}{4} \).
- Find \( a \) and \( b \) that satisfy both equations. In this case, \( a = 1 \) and \( b = 1 \) work, leading to: \[ \sqrt{2 + \sqrt{3}} = \sqrt{1} + \sqrt{1} = 1 + 1 = 2 \]
2. Using Algebraic Identities
Algebraic identities can simplify expressions involving radicals. Familiarity with these can make the process more efficient.
For example, use the difference of squares to simplify:
\[
(\sqrt{a} - \sqrt{b})(\sqrt{a} + \sqrt{b}) = a - b
\]
To rationalize \( \frac{1}{\sqrt{5} - \sqrt{2}} \):
- Multiply by the conjugate: \[ \frac{1}{\sqrt{5} - \sqrt{2}} \times \frac{\sqrt{5} + \sqrt{2}}{\sqrt{5} + \sqrt{2}} = \frac{\sqrt{5} + \sqrt{2}}{5 - 2} = \frac{\sqrt{5} + \sqrt{2}}{3} \]
3. Simplifying Expressions with Multiple Radicals
When dealing with expressions involving multiple radicals, look for common factors and opportunities to combine or separate radicals.
For instance, simplify \( \frac{\sqrt{72} - \sqrt{18}}{\sqrt{2}} \):
- Simplify the radicals in the numerator: \[ \sqrt{72} = 6\sqrt{2}, \quad \sqrt{18} = 3\sqrt{2} \]
- Combine like terms: \[ \frac{6\sqrt{2} - 3\sqrt{2}}{\sqrt{2}} = \frac{3\sqrt{2}}{\sqrt{2}} \]
- Divide by \( \sqrt{2} \): \[ 3 \]
4. Approximating Radicals
Sometimes, it's necessary to approximate radicals, especially when exact simplification is difficult or unnecessary. Understanding common approximations can be helpful.
For example:
\[
\sqrt{2} \approx 1.414, \quad \sqrt{3} \approx 1.732, \quad \sqrt{5} \approx 2.236
\]
These approximations can simplify calculations and provide quick estimates for complex problems.
5. Using Rational Exponents
Radicals can be expressed using rational exponents, which sometimes makes simplification easier. The equivalence \( \sqrt[n]{a} = a^{1/n} \) can transform radicals into exponential form.
For example, simplify \( \sqrt[3]{x^5} \):
\ul>
6. Applying the Binomial Theorem
The binomial theorem can simplify expressions involving the sum or difference of radicals raised to a power. This is particularly useful for expanding and simplifying binomial expressions.
For instance, expand \( (\sqrt{a} + \sqrt{b})^2 \):
- Use the binomial expansion: \[ (\sqrt{a} + \sqrt{b})^2 = a + 2\sqrt{ab} + b \]
Practice Problems for Advanced Techniques
Challenge yourself with these advanced practice problems:
- Simplify the nested radical \( \sqrt{7 + 4\sqrt{3}} \).
- Use rational exponents to simplify \( \sqrt[4]{x^8 y^{12}} \).
- Expand and simplify \( (\sqrt{3} + \sqrt{2})^3 \).
- Simplify the expression \( \frac{\sqrt{a} + \sqrt{b}}{\sqrt{a} - \sqrt{b}} \).
- Approximate \( \sqrt{45} \) to two decimal places.
By mastering these advanced techniques and tips, you can handle more complex problems involving radicals with confidence and efficiency.
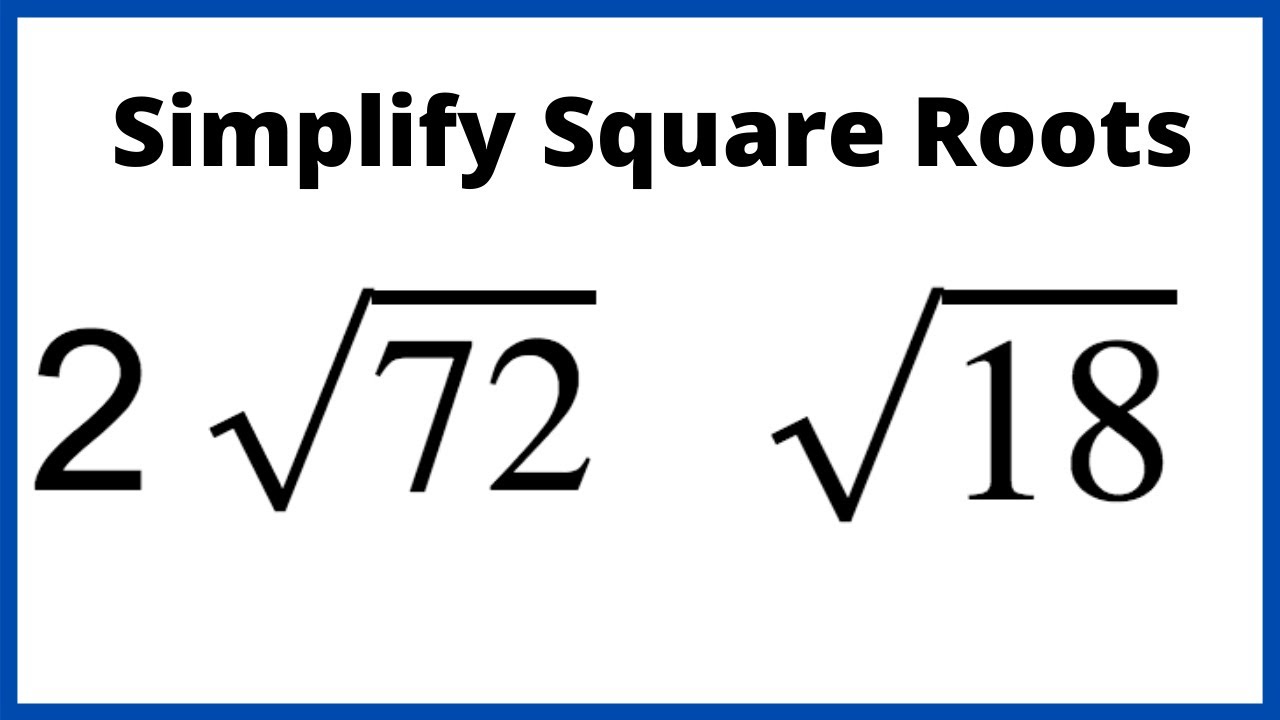
Conclusion and Summary
Simplifying radicals and square roots is a fundamental skill in algebra that provides a foundation for solving a wide range of mathematical problems. By mastering these techniques, you can handle expressions and equations more efficiently and accurately. Let's recap the key points discussed in this guide:
1. Understanding Radicals
- Radicals represent roots of numbers, with square roots being the most common.
- The notation \( \sqrt[n]{a} \) denotes the \( n \)-th root of \( a \), and \( \sqrt{a} \) specifically represents the square root of \( a \).
- Basic properties of radicals include:
- \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^n = a^{n/2}\)
2. Simplifying Radicals
- Simplify radicals by factoring out perfect squares or higher powers for higher-order roots.
- Combine like terms for expressions involving multiple radicals.
- Practice using methods like the prime factorization and pairing method to streamline the simplification process.
3. Rationalizing Denominators
- Rationalizing involves eliminating radicals from the denominator of a fraction.
- Multiply by the conjugate or an appropriate radical to achieve a rational denominator.
- This technique is crucial for simplifying expressions and solving equations efficiently.
4. Avoiding Common Mistakes
- Ensure correct application of properties of radicals, especially when combining or separating them.
- Be cautious with negative numbers under even roots and always simplify expressions fully.
- Avoid distributing a radical over addition or subtraction incorrectly.
5. Applying Simplified Radicals in Algebra
- Simplified radicals are essential for solving quadratic equations and other algebraic expressions.
- They play a significant role in geometry, trigonometry, and real-world problem-solving.
- Understanding these applications helps in grasping more complex mathematical concepts.
6. Advanced Techniques and Tips
- Simplify nested radicals and use algebraic identities to handle complex expressions.
- Express radicals using rational exponents for easier manipulation and simplification.
- Approximate radicals where exact simplification is not possible or practical.
In summary, mastering the simplification of radicals and square roots opens up numerous avenues in algebra and beyond. It enhances problem-solving skills and provides deeper insights into mathematical relationships. Practice regularly with various types of problems to strengthen your understanding and proficiency.
As you continue your mathematical journey, remember that the techniques and principles you have learned here will serve as valuable tools in many areas of study and real-life applications.
Additional Resources and Further Reading
For further exploration of simplifying radicals and square roots, here are some valuable resources and additional reading materials:
-
This resource provides a comprehensive guide on using the product and quotient properties to simplify radical expressions, complete with examples and practice problems.
-
An extensive tutorial covering various methods of simplifying radical expressions, including step-by-step examples for different types of radicals.
-
This page explains numerical simplification of radicals, focusing on identifying and using the largest perfect square factors for simplification.
-
A detailed explanation of simplifying algebraic radicals, including handling variables and rationalizing denominators.
-
Khan Academy offers video tutorials and exercises on simplifying square roots, perfect for visual learners and those seeking interactive practice.
-
Purplemath provides clear explanations and step-by-step instructions for simplifying radical expressions, including tips on common mistakes to avoid.
Phương Pháp Dễ Dàng Đơn Giản Hóa Căn Thức
READ MORE:
Đơn Giản Hóa Căn Bậc Hai | Số Mũ, Căn Thức, và Ký Hiệu Khoa Học | Tiền Đại Số | Khan Academy







