Topic simplifying a square root: Simplifying a square root is a fundamental skill in mathematics, essential for algebra and higher-level math. This guide will walk you through the basics, rules, and techniques for simplifying square roots, providing clear examples and practical tips to enhance your understanding and proficiency.
Table of Content
- Simplifying Square Roots
- Introduction to Square Roots
- Basic Concepts and Definitions
- Product Rule for Radicals
- Quotient Rule for Radicals
- Examples of Simplifying Square Roots
- Simplifying Non-Numerical Radicals
- Practice Problems and Solutions
- Common Mistakes and How to Avoid Them
- Advanced Techniques for Simplifying Square Roots
- Applications of Simplified Square Roots in Algebra
- YOUTUBE:
Simplifying Square Roots
Simplifying square roots is an essential skill in algebra. The goal is to express the square root in its simplest form, making calculations easier and results more understandable. Here are some key concepts and examples to help you master this process.
Basic Rule
The fundamental rule for simplifying square roots is:
\(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
Examples
- Example 1: Simplify \(\sqrt{12}\)
- Factor 12 into \(4 \times 3\)
- Apply the rule: \(\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3}\)
- Simplify: \(\sqrt{4} = 2\), so \(\sqrt{12} = 2\sqrt{3}\)
- Example 2: Simplify \(\sqrt{45}\)
- Factor 45 into \(9 \times 5\)
- Apply the rule: \(\sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5}\)
- Simplify: \(\sqrt{9} = 3\), so \(\sqrt{45} = 3\sqrt{5}\)
Combining Radicals
- Example: Simplify \(\sqrt{6} \cdot \sqrt{15}\)
- Combine under one radical: \(\sqrt{6 \cdot 15} = \sqrt{90}\)
- Factor 90: \(\sqrt{90} = \sqrt{9 \cdot 10} = \sqrt{9} \cdot \sqrt{10}\)
- Simplify: \(\sqrt{9} = 3\), so \(\sqrt{90} = 3\sqrt{10}\)
Fractions
The same rule applies to fractions:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Example: Simplify \(\sqrt{\frac{30}{10}}\)
- Combine under one radical: \(\sqrt{\frac{30}{10}} = \sqrt{3}\)
Additional Resources
Practice Problems
- Simplify \(\sqrt{50}\)
- Simplify \(\sqrt{72}\)
- Simplify \(\sqrt{\frac{75}{3}}\)
Try these problems and check your answers using the rules and examples provided.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, representing the inverse operation of squaring a number. Essentially, the square root of a number \( n \), denoted as \( \sqrt{n} \), is the value that, when multiplied by itself, gives \( n \). For example, the square root of 25 is 5 because \( 5 \times 5 = 25 \).
Understanding square roots involves recognizing perfect squares and simplifying non-perfect square roots. Perfect squares are numbers like 1, 4, 9, 16, 25, etc., where the square root is an integer. Simplifying square roots that are not perfect squares requires breaking down the number into its prime factors and applying the product rule for radicals.
For instance, to simplify \( \sqrt{50} \), we factor 50 into its prime components: \( 50 = 25 \times 2 \). Recognizing that 25 is a perfect square (\( 5^2 \)), we simplify \( \sqrt{50} \) to \( 5\sqrt{2} \).
Another example is simplifying \( \sqrt{45} \). First, factor 45 into \( 9 \times 5 \). Since 9 is a perfect square (\( 3^2 \)), \( \sqrt{45} \) simplifies to \( 3\sqrt{5} \). This method can be extended to more complex expressions, including those with multiple square roots or fractions.
Understanding and simplifying square roots is crucial in various mathematical applications, from algebra to calculus, and provides a foundation for solving equations involving quadratic terms and beyond.
Basic Concepts and Definitions
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol √. For a non-negative number a, the square root is written as √a or a^(1/2).
- Square Root Symbol: The symbol
√is used to denote the square root. For example,√25represents the square root of 25. - Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because they are squares of whole numbers (12, 22, 32, 42, and 52 respectively).
- Principal Square Root: The non-negative square root of a number is called the principal square root. For example, the principal square root of 9 is 3, even though -3 is also a square root of 9.
- Radical Expression: An expression that includes a square root is called a radical expression. For example,
√50is a radical expression.
To simplify a square root, you can use the following steps:
- Factor the Number: Write the number under the radical as a product of its prime factors. For example, 50 can be factored into 2 × 5 × 5.
- Group the Factors: Group the factors into pairs. For 50, this would be (5 × 5) × 2.
- Simplify the Radical: Take one factor from each pair out of the radical. So,
√(5 × 5) × 2simplifies to 5√2.
Let's look at some examples to understand this better:
| Expression | Factorization | Simplified Form |
|---|---|---|
√36 |
6 × 6 | 6 |
√72 |
2 × 2 × 2 × 3 × 3 | 6√2 |
√128 |
2 × 2 × 2 × 2 × 2 × 2 × 2 | 8√2 |
Product Rule for Radicals
The product rule for radicals is a fundamental property that helps in simplifying the square roots of products. It states that the square root of a product is equal to the product of the square roots of each factor. This can be expressed mathematically as:
Here are the steps to simplify a square root using the product rule:
- Factor any perfect squares from the radicand.
- Write the radical expression as a product of radical expressions.
- Simplify each radical expression.
Let's look at a few examples to illustrate this rule:
Example 1: Simplifying
- Factor the radicand:
- Apply the product rule:
- Simplify:
- Final result:
Example 2: Simplifying
- Factor the radicand:
- Apply the product rule:
- Simplify:
- Final result:
Combining Multiple Radicals
The product rule can also be used to combine multiple radicals into a single radical expression. For example:
Example: Simplifying
- Combine the radicals:
- Simplify:
- Final result:
By following these steps and applying the product rule, you can simplify a wide range of square root expressions with ease.
Quotient Rule for Radicals
The Quotient Rule for Radicals allows us to simplify the square root of a fraction by expressing it as the quotient of two separate square roots. This can make it easier to simplify the expression. The rule states:
$$\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$$
Here are the steps to apply the quotient rule for simplifying radicals:
- Write the radical expression as the quotient of two separate radicals.
- Simplify the numerator and the denominator separately.
Let's look at some examples:
| Example 1 | Simplify \( \sqrt{\frac{9}{16}} \) |
| Step 1: | Write as the quotient of two radicals: \( \frac{\sqrt{9}}{\sqrt{16}} \) |
| Step 2: | Simplify each radical: \( \frac{3}{4} \) |
| Answer: | \( \sqrt{\frac{9}{16}} = \frac{3}{4} \) |
| Example 2 | Simplify \( \sqrt{\frac{45x^5}{y^4}} \) |
| Step 1: | Write as the quotient of two radicals: \( \frac{\sqrt{45x^5}}{\sqrt{y^4}} \) |
| Step 2: | Simplify each radical: \( \frac{\sqrt{9x^4 \cdot 5x}}{y^2} \) |
| Step 3: | Further simplify: \( \frac{3x^2\sqrt{5x}}{y^2} \) |
| Answer: | \( \sqrt{\frac{45x^5}{y^4}} = \frac{3x^2\sqrt{5x}}{y^2} \) |
By following these steps, you can effectively simplify any radical expression that involves a quotient.
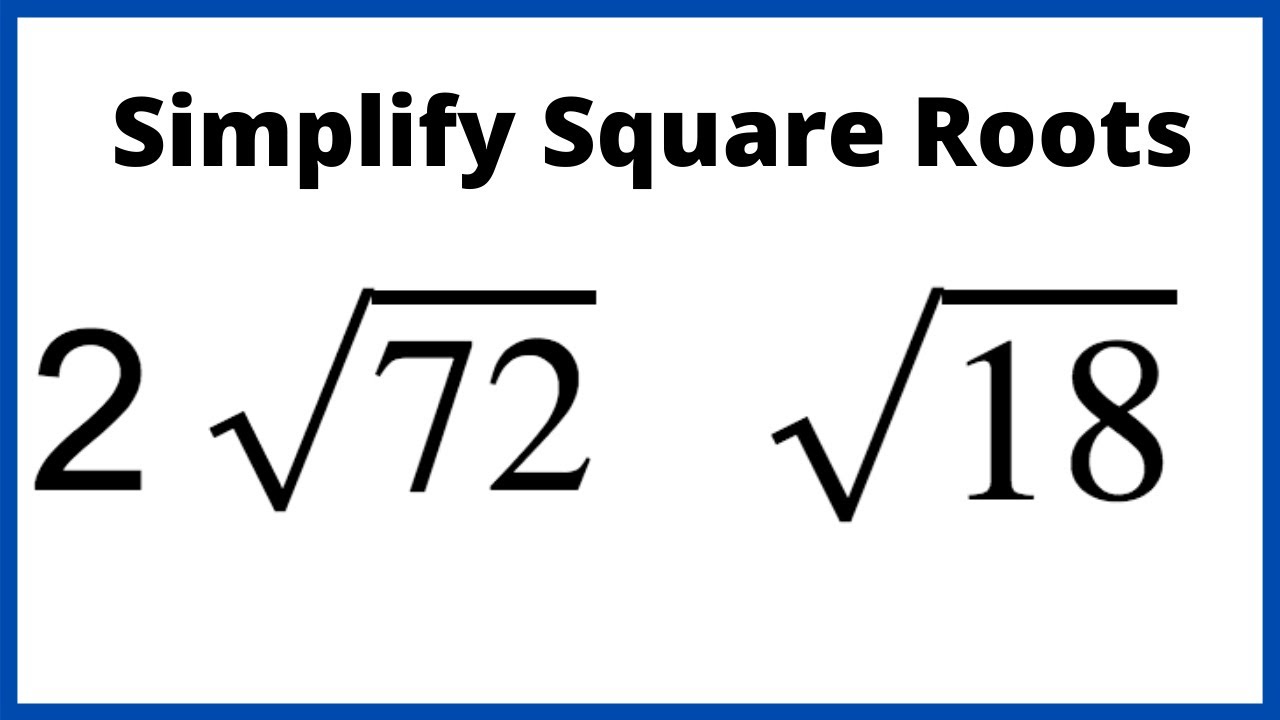
Examples of Simplifying Square Roots
Here are some examples illustrating the process of simplifying square roots:
- Simplify \( \sqrt{16} \):
- Simplify \( \sqrt{25} \):
- Simplify \( \sqrt{72} \):
- Simplify \( \sqrt{200} \):
We know that \( \sqrt{16} \) equals 4, since 4 multiplied by itself gives 16.
Similarly, \( \sqrt{25} \) equals 5, as 5 multiplied by itself results in 25.
To simplify \( \sqrt{72} \), we can factor 72 into its prime factors: \( 72 = 2^3 \times 3^2 \).
Now, since we're dealing with a square root, we can pair up the factors. We have \( 2^3 \) and \( 3^2 \).
For each pair, we take one factor out. So, \( \sqrt{72} = \sqrt{2^3} \times \sqrt{3^2} \).
That simplifies to \( 2\sqrt{2} \times 3\sqrt{3} \).
Finally, multiplying, we get \( 6\sqrt{2\cdot3} \).
Therefore, \( \sqrt{72} = 6\sqrt{6} \).
Similarly, we factor 200 into its prime factors: \( 200 = 2^3 \times 5^2 \).
Pairing up the factors, we have \( 2^3 \) and \( 5^2 \).
So, \( \sqrt{200} = \sqrt{2^3} \times \sqrt{5^2} \).
That simplifies to \( 2\sqrt{2} \times 5\sqrt{5} \).
Multiplying, we get \( 10\sqrt{2\cdot5} \).
Hence, \( \sqrt{200} = 10\sqrt{10} \).
Simplifying Non-Numerical Radicals
Non-numerical radicals often involve variables, and simplifying them follows a similar process as with numerical radicals. Here are the steps to simplify non-numerical radicals:
- Identify the radicand:
The radicand is the expression inside the radical symbol. For example, in the radical \( \sqrt{18x^4y^2} \), the radicand is \( 18x^4y^2 \).
- Factor the radicand into prime factors:
Break down the radicand into its prime factors. For example, \( 18x^4y^2 \) can be factored as \( 2 \cdot 3^2 \cdot x^4 \cdot y^2 \).
- Apply the product rule for radicals:
The product rule states that \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \). Using this rule, we can separate the factors under the radical:
\( \sqrt{2 \cdot 3^2 \cdot x^4 \cdot y^2} = \sqrt{2} \cdot \sqrt{3^2} \cdot \sqrt{x^4} \cdot \sqrt{y^2} \)
- Simplify each radical separately:
Simplify each individual radical:
- \( \sqrt{3^2} = 3 \) because \( 3^2 \) is a perfect square.
- \( \sqrt{x^4} = x^2 \) because \( x^4 \) is a perfect square.
- \( \sqrt{y^2} = y \) because \( y^2 \) is a perfect square.
So, \( \sqrt{2} \) remains as it is since it cannot be simplified further.
- Combine the simplified parts:
After simplifying each radical, multiply the simplified parts together:
\( \sqrt{2} \cdot 3 \cdot x^2 \cdot y = 3x^2y\sqrt{2} \)
Therefore, the simplified form of \( \sqrt{18x^4y^2} \) is \( 3x^2y\sqrt{2} \).
Here are a few more examples:
- \( \sqrt{50a^6b^3} \)
- Factor the radicand: \( 50a^6b^3 = 2 \cdot 5^2 \cdot a^6 \cdot b^3 \)
- Apply the product rule: \( \sqrt{2} \cdot \sqrt{5^2} \cdot \sqrt{a^6} \cdot \sqrt{b^3} \)
- Simplify each radical: \( \sqrt{2} \cdot 5 \cdot a^3 \cdot b\sqrt{b} \)
- Combine: \( 5a^3b\sqrt{2b} \)
- \( \sqrt{72m^5n^2} \)
- Factor the radicand: \( 72m^5n^2 = 2^3 \cdot 3^2 \cdot m^5 \cdot n^2 \)
- Apply the product rule: \( \sqrt{2^3} \cdot \sqrt{3^2} \cdot \sqrt{m^5} \cdot \sqrt{n^2} \)
- Simplify each radical: \( 2\sqrt{2} \cdot 3 \cdot m^2\sqrt{m} \cdot n \)
- Combine: \( 6m^2n\sqrt{2m} \)
By following these steps, you can simplify any non-numerical radical expression. Practice with different expressions to become more familiar with the process.
Practice Problems and Solutions
Here are some practice problems along with step-by-step solutions to help you master the skill of simplifying square roots.
Problem 1
Simplify \( \sqrt{50} \)
Solution:
- Factor the number inside the square root into its prime factors: \( 50 = 2 \times 5^2 \)
- Identify the perfect squares: \( 5^2 \)
- Rewrite the square root: \( \sqrt{50} = \sqrt{2 \times 5^2} = \sqrt{2} \times \sqrt{5^2} \)
- Simplify: \( \sqrt{50} = \sqrt{2} \times 5 = 5\sqrt{2} \)
Problem 2
Simplify \( \sqrt{72} \)
Solution:
- Factor the number inside the square root into its prime factors: \( 72 = 2^3 \times 3^2 \)
- Identify the perfect squares: \( 3^2 \)
- Rewrite the square root: \( \sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{2^3} \times \sqrt{3^2} \)
- Simplify: \( \sqrt{72} = \sqrt{8} \times 3 = 2\sqrt{2} \times 3 = 6\sqrt{2} \)
Problem 3
Simplify \( \sqrt{32} \)
Solution:
- Factor the number inside the square root into its prime factors: \( 32 = 2^5 \)
- Identify the perfect squares: \( 2^4 \)
- Rewrite the square root: \( \sqrt{32} = \sqrt{2^4 \times 2} = \sqrt{2^4} \times \sqrt{2} \)
- Simplify: \( \sqrt{32} = 4\sqrt{2} \)
Problem 4
Simplify \( \sqrt{18} \)
Solution:
- Factor the number inside the square root into its prime factors: \( 18 = 2 \times 3^2 \)
- Identify the perfect squares: \( 3^2 \)
- Rewrite the square root: \( \sqrt{18} = \sqrt{2 \times 3^2} = \sqrt{2} \times \sqrt{3^2} \)
- Simplify: \( \sqrt{18} = \sqrt{2} \times 3 = 3\sqrt{2} \)
Problem 5
Simplify \( \sqrt{200} \)
Solution:
- Factor the number inside the square root into its prime factors: \( 200 = 2^3 \times 5^2 \)
- Identify the perfect squares: \( 5^2 \)
- Rewrite the square root: \( \sqrt{200} = \sqrt{2^3 \times 5^2} = \sqrt{2^3} \times \sqrt{5^2} \)
- Simplify: \( \sqrt{200} = \sqrt{8} \times 5 = 2\sqrt{2} \times 5 = 10\sqrt{2} \)
These practice problems should help solidify your understanding of how to simplify square roots by identifying and extracting perfect square factors.
Common Mistakes and How to Avoid Them
When simplifying square roots, students often encounter several common mistakes. Understanding these errors and learning how to avoid them is crucial for mastering this mathematical concept. Below are some of the most frequent mistakes and tips on how to prevent them:
- Not Fully Simplifying the Radical: Always look for the largest perfect square factor of the radicand. For example,
- \(\sqrt{32} = \sqrt{16 \times 2} = 4\sqrt{2}\) not \(2\sqrt{8}\)
- Misapplying the Product and Quotient Rules: Only multiply or divide the radicands if you are performing the same operation on the entire radicals.
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Forgetting to Rationalize the Denominator: Ensure no radicals are left in the denominator by multiplying the numerator and denominator by the radical.
- \(\frac{1}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
- Ignoring the Sign of the Variable under the Square Root: Remember that the square root of a squared variable is the absolute value of the variable.
- \(\sqrt{x^2} = |x|\)
- Combining Unlike Terms: Only combine radicals with the same radicand.
- \(\sqrt{3} + \sqrt{3} = 2\sqrt{3}\)
- \(\sqrt{3} + \sqrt{5} \neq \sqrt{8}\)
- Incorrectly Handling Coefficients: Apply multiplication correctly when dealing with variables and their powers.
- \(2\sqrt{3} \times 3\sqrt{2} = 6\sqrt{6}\)
- Misinterpreting the Square Root Symbol: The square root symbol represents the principal (non-negative) root.
- \(\sqrt{9} = 3\), but \(x^2 = 9\) has solutions \(x = \pm 3\)
By being mindful of these common mistakes and practicing correct techniques, students can improve their accuracy and efficiency in simplifying square root expressions.

Advanced Techniques for Simplifying Square Roots
In addition to the basic methods of simplifying square roots, there are several advanced techniques that can help you handle more complex expressions effectively. These techniques often involve a deeper understanding of algebraic principles and properties of radicals.
1. Rationalizing the Denominator
When a square root appears in the denominator, it's often useful to rationalize the denominator. This process involves eliminating the square root from the denominator by multiplying both the numerator and the denominator by an appropriate value.
For example:
\[
\frac{1}{\sqrt{2}} \quad \text{can be rationalized by multiplying by} \quad \frac{\sqrt{2}}{\sqrt{2}}
\]
\[
\frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}
\]
2. Using the Difference of Squares
This technique is particularly useful when dealing with expressions that involve the difference of two squares, such as \(\sqrt{a} - \sqrt{b}\).
For example:
\[
\frac{1}{\sqrt{a} - \sqrt{b}} \quad \text{can be simplified by multiplying by} \quad \frac{\sqrt{a} + \sqrt{b}}{\sqrt{a} + \sqrt{b}}
\]
\[
\frac{1 \cdot (\sqrt{a} + \sqrt{b})}{(\sqrt{a} - \sqrt{b})(\sqrt{a} + \sqrt{b})} = \frac{\sqrt{a} + \sqrt{b}}{a - b}
\]
3. Simplifying Nested Radicals
Sometimes, you may encounter nested radicals, such as \(\sqrt{1 + \sqrt{2}}\). These can often be simplified by expressing the inner radical in a different form.
For example:
\[
\sqrt{3 + 2\sqrt{2}} \quad \text{can be simplified by recognizing it as} \quad \sqrt{(\sqrt{2} + 1)^2}
\]
\[
= \sqrt{2} + 1
\]
4. Using Algebraic Identities
Algebraic identities can simplify the process of dealing with square roots. For instance, using the identity \((a + b)^2 = a^2 + 2ab + b^2\) can help simplify expressions under the square root.
For example:
\[
\sqrt{4x^2 + 4x + 1} \quad \text{can be simplified by recognizing it as} \quad \sqrt{(2x + 1)^2}
\]
\[
= 2x + 1
\]
5. Prime Factorization Method
This method involves breaking down the number under the square root into its prime factors, which can then be simplified.
For example:
\[
\sqrt{72} \quad \text{can be broken down into} \quad \sqrt{2^3 \times 3^2}
\]
\[
= \sqrt{(2^2 \times 3^2) \times 2} = 6\sqrt{2}
\]
Practice Problems
- Simplify: \(\sqrt{50}\)
Solution: \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\) - Simplify: \(\sqrt{200}\)
Solution: \(\sqrt{200} = \sqrt{100 \times 2} = 10\sqrt{2}\) - Simplify: \(\sqrt{72}\)
Solution: \(\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}\) - Simplify: \(\frac{3}{\sqrt{5}}\)
Solution: \(\frac{3}{\sqrt{5}} = \frac{3 \cdot \sqrt{5}}{\sqrt{5} \cdot \sqrt{5}} = \frac{3\sqrt{5}}{5}\)
By mastering these advanced techniques, you can simplify a wide range of square root expressions, making complex calculations more manageable.
Applications of Simplified Square Roots in Algebra
Simplified square roots play a crucial role in various algebraic applications. Understanding how to simplify square roots allows for easier manipulation and solving of algebraic equations. Below are some key applications:
-
Simplifying Expressions:
When dealing with algebraic expressions, simplified square roots can make equations less complex and more manageable. For example:
\[
\text{Simplify } \sqrt{50x^2} = \sqrt{25 \cdot 2 \cdot x^2} = 5x\sqrt{2}
\] -
Solving Quadratic Equations:
Quadratic equations often require taking square roots to find solutions. Simplifying square roots is essential in the process:
\[
\text{Solve } x^2 = 45 \implies x = \pm\sqrt{45} = \pm\sqrt{9 \cdot 5} = \pm 3\sqrt{5}
\] -
Rationalizing Denominators:
Rationalizing denominators involves simplifying the expression so that no radicals remain in the denominator:
\[
\text{Rationalize } \frac{1}{\sqrt{3}} \implies \frac{1}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}
\] -
Distance Formula:
The distance formula, used to find the distance between two points in a coordinate plane, often involves simplifying square roots:
\[
\text{Distance } = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]Example:
\[
\text{Distance between } (1,2) \text{ and } (4,6) = \sqrt{(4-1)^2 + (6-2)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\] -
Geometric Applications:
Simplified square roots are used in calculating areas and volumes of geometric shapes, especially when dealing with diagonals and sides of squares and cubes:
\[
\text{Diagonal of a square with side } s = s\sqrt{2}
\]Example:
\[
\text{Diagonal of a square with side 4} = 4\sqrt{2}
\]
Làm Thế Nào Để Đơn Giản Hóa Căn Bậc Hai
READ MORE:
Đơn Giản Hóa Căn Bậc Hai | Toán Học với Thầy J








