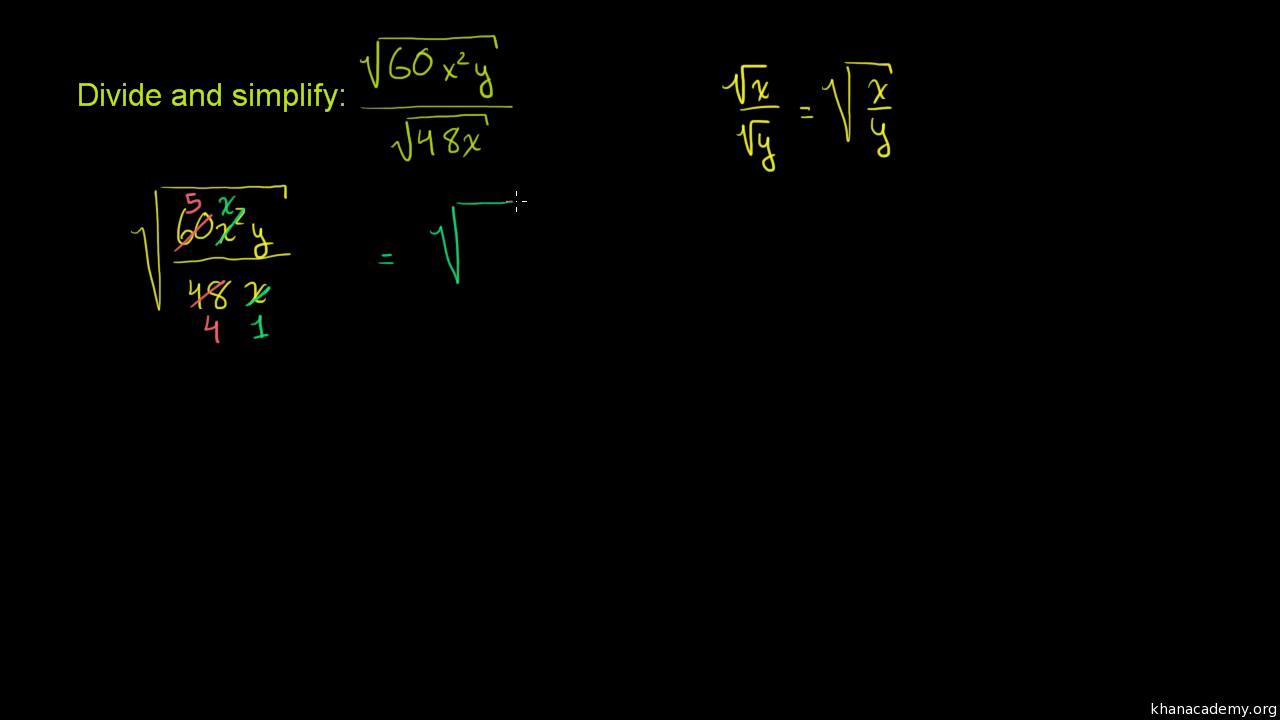Master Simplifying Radical Expressions: Step-by-Step Examples and Techniques

Radical expressions often require simplification for easier manipulation. Below are some common examples illustrating the process.

Example 1: Simplifying a Single Radical

Consider the expression: \( \sqrt{50} \).

Steps to simplify:

1. Find the prime factorization of 50: \( 50 = 2 \times 5^2 \).
2. Rewrite the radical expression using the prime factors: \( \sqrt{50} = \sqrt{2 \times 5^2} \).
3. Since \( 5^2 \) is a perfect square, it can be taken out of the radical: \( \sqrt{2 \times 5^2} = 5\sqrt{2} \).

Therefore, \( \sqrt{50} = 5\sqrt{2} \).

Example 2: Simplifying a Radical with Variables

Consider the expression: \( \sqrt{18x^3} \).

Steps to simplify:

1. Find the prime factorization of 18: \( 18 = 2 \times 3^2 \).
2. Rewrite the expression: \( \sqrt{18x^3} = \sqrt{2 \times 3^2 \times x^3} \).
3. Separate the perfect squares: \( \sqrt{2 \times 3^2 \times x^3} = 3x\sqrt{2x} \).

Therefore, \( \sqrt{18x^3} = 3x\sqrt{2x} \).

Example 3: Simplifying a Radical Fraction

Consider the expression: \( \frac{\sqrt{48}}{\sqrt{3}} \).

Steps to simplify:

1. Combine the radicals: \( \frac{\sqrt{48}}{\sqrt{3}} = \sqrt{\frac{48}{3}} \).
2. Simplify the fraction under the radical: \( \sqrt{\frac{48}{3}} = \sqrt{16} \).
3. Since 16 is a perfect square, simplify it: \( \sqrt{16} = 4 \).

Therefore, \( \frac{\sqrt{48}}{\sqrt{3}} = 4 \).

Example 4: Simplifying a Sum of Radicals

Consider the expression: \( \sqrt{27} + 2\sqrt{12} \).

Steps to simplify:

1. Simplify each radical separately:
   • \( \sqrt{27} = \sqrt{3^3} = 3\sqrt{3} \)
   • \( 2\sqrt{12} = 2\sqrt{4 \times 3} = 2 \times 2\sqrt{3} = 4\sqrt{3} \)
2. Combine the simplified radicals: \( 3\sqrt{3} + 4\sqrt{3} = 7\sqrt{3} \).

Therefore, \( \sqrt{27} + 2\sqrt{12} = 7\sqrt{3} \).

Example 5: Rationalizing the Denominator

Consider the expression: \( \frac{5}{\sqrt{2}} \).

Steps to rationalize the denominator:

1. Multiply the numerator and the denominator by \( \sqrt{2} \): \( \frac{5}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{5\sqrt{2}}{2} \).

Therefore, \( \frac{5}{\sqrt{2}} = \frac{5\sqrt{2}}{2} \).

Radical expressions, often involving roots such as square roots and cube roots, play a crucial role in algebra and higher mathematics. Simplifying these expressions is essential for solving equations and understanding mathematical relationships. This section provides a detailed introduction to radical expressions, their components, and basic principles.

A radical expression includes a radical symbol (√) and a radicand (the number or expression inside the radical). For example, in \( \sqrt{25} \), the radical symbol is √ and the radicand is 25.

Here are the key components and steps to understanding and simplifying radical expressions:

• Radical Symbol: The symbol √, indicating the root.
• Radicand: The number or expression inside the radical symbol.
• Index: The small number outside and to the left of the radical symbol, indicating the degree of the root. If no number is present, the index is assumed to be 2 (square root).

Steps to Simplify Radical Expressions:

1. Prime Factorization: Break down the radicand into its prime factors. For example, \( 50 = 2 \times 5^2 \).
2. Identify Perfect Squares: Identify and separate perfect squares within the radicand. For instance, in \( \sqrt{50} \), \( 5^2 \) is a perfect square.
3. Extract the Square Root: Take the square root of the perfect square factors and place them outside the radical. For example, \( \sqrt{50} = 5\sqrt{2} \).

Radical expressions can also involve variables. The steps to simplify these are similar:

1. Break down the radicand, including any variable expressions, into prime factors.
2. Identify and separate perfect squares involving both constants and variables.
3. Extract the square root of these perfect squares, simplifying the expression.

Example: Simplifying \( \sqrt{18x^3} \)

1. Prime factorization: \( 18 = 2 \times 3^2 \) and \( x^3 = x^2 \times x \).
2. Separate perfect squares: \( \sqrt{18x^3} = \sqrt{2 \times 3^2 \times x^2 \times x} \).
3. Extract square roots: \( \sqrt{18x^3} = 3x\sqrt{2x} \).

Understanding these fundamental concepts and steps will enable you to tackle more complex radical expressions with confidence.

Radicals are expressions that include a root symbol, such as a square root or cube root. Simplifying these expressions involves understanding and applying a few key concepts and rules. Here we will outline the foundational principles necessary for working with radicals effectively.

• Definition: A radical expression contains a root symbol (√) with a radicand, which is the value inside the root. For example, in √16, 16 is the radicand.
• Product Rule: The product rule states that the square root of a product is equal to the product of the square roots of the factors. Mathematically, this is expressed as:
  • \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
• Quotient Rule: The quotient rule states that the square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator:
  • \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}, \text{where } b \neq 0\)
• Simplifying Radicals: Simplification involves reducing the radicand to its simplest form. This can be done by factoring the radicand into prime factors and then applying the product rule. For example:
  • \(\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}\)
• Dealing with Variables: When simplifying radicals with variables, treat the variables similarly to numerical factors. For instance:
  • \(\sqrt{x^4} = x^2\)
  • \(\sqrt{a^2 \cdot b^3} = a \cdot b \cdot \sqrt{b}\)
• Absolute Value: When dealing with even roots, the result should be non-negative, often requiring the use of absolute values. For example:
  • \(\sqrt{x^2} = |x|\)
• Common Mistakes: Be cautious of the following errors:
  • \(\sqrt{a + b} \neq \sqrt{a} + \sqrt{b}\)
  • \(\sqrt{a - b} \neq \sqrt{a} - \sqrt{b}\)

Understanding these basic concepts and rules is crucial for simplifying radical expressions accurately and efficiently.

Prime factorization is a useful method for simplifying radical expressions. This involves expressing the number inside the radical (the radicand) as a product of its prime factors and then simplifying.

Steps to Simplify Radicals Using Prime Factorization

1. Factor the radicand into its prime factors.
2. Group the prime factors into pairs.
3. Move each pair of prime factors out of the radical as a single factor.
4. Multiply the factors outside the radical.
5. Simplify the remaining factors inside the radical if possible.

Examples

Example 1: Simplify \( \sqrt{72} \)

• Factor 72 into its prime factors: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
• Group the prime factors into pairs: \( 72 = (2 \times 2) \times (3 \times 3) \times 2 \).
• Move each pair out of the radical: \( \sqrt{72} = 2 \times 3 \times \sqrt{2} \).
• Multiply the factors outside the radical: \( 2 \times 3 = 6 \).
• Simplified result: \( \sqrt{72} = 6 \sqrt{2} \).

Example 2: Simplify \( \sqrt{50} \)

• Factor 50 into its prime factors: \( 50 = 2 \times 5 \times 5 \).
• Group the prime factors into pairs: \( 50 = 2 \times (5 \times 5) \).
• Move the pair out of the radical: \( \sqrt{50} = 5 \sqrt{2} \).
• Simplified result: \( \sqrt{50} = 5 \sqrt{2} \).

Prime Factorization with Variables

When simplifying radicals that contain variables, use the same process. Treat the exponents of the variables as factors and group them accordingly.

Example 3: Simplify \( \sqrt{x^8 y^3} \)

• Factor the variables: \( x^8 = x^4 \times x^4 \) and \( y^3 = y^2 \times y \).
• Group the factors: \( \sqrt{x^8 y^3} = \sqrt{(x^4 \times x^4) \times (y^2 \times y)} \).
• Move the pairs out of the radical: \( \sqrt{x^8 y^3} = x^4 y \sqrt{y} \).
• Simplified result: \( \sqrt{x^8 y^3} = x^4 y \sqrt{y} \).

Prime factorization is a powerful technique for simplifying radicals, especially when dealing with large numbers or variables. By breaking down the radicand into its prime factors, you can easily identify and extract perfect squares, leading to a simplified radical expression.

To simplify a single radical expression, follow these steps:

1. Find the Prime Factorization:

   Break down the number under the radical into its prime factors.

   Example: \(\sqrt{72} = \sqrt{2 \times 2 \times 2 \times 3 \times 3}\)

2. Group the Factors:

   Group the prime factors in pairs.

   Example: \(\sqrt{2 \times 2 \times 2 \times 3 \times 3} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2}\)

3. Simplify the Radical:

   Take out each pair of identical factors as a single factor outside the radical.

   Example: \(\sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)

Let's look at another example:

• Example: Simplify \(\sqrt{50}\)
  1. Prime factorization: \(50 = 2 \times 5 \times 5\)
  2. Group the factors: \(\sqrt{2 \times 5 \times 5} = \sqrt{(5 \times 5) \times 2}\)
  3. Simplify the radical: \(\sqrt{(5 \times 5) \times 2} = 5\sqrt{2}\)

Another method involves recognizing perfect squares:

1. Identify Perfect Squares:

   Find the largest perfect square factor of the radicand.

   Example: \(\sqrt{180} = \sqrt{36 \times 5}\)

2. Apply the Product Rule:

   Use the product rule of radicals to simplify.

   \(\sqrt{36 \times 5} = \sqrt{36} \times \sqrt{5} = 6\sqrt{5}\)

Practice Problems:

• Simplify: \(\sqrt{32}\)
  • Prime factorization: \(32 = 2 \times 2 \times 2 \times 2 \times 2\)
  • Group the factors: \(\sqrt{(2 \times 2) \times (2 \times 2) \times 2}\)
  • Simplify the radical: \(\sqrt{(2 \times 2) \times (2 \times 2) \times 2} = 2 \times 2 \times \sqrt{2} = 4\sqrt{2}\)
• Simplify: \(\sqrt{75}\)
  • Prime factorization: \(75 = 3 \times 5 \times 5\)
  • Group the factors: \(\sqrt{3 \times (5 \times 5)}\)
  • Simplify the radical: \(\sqrt{3 \times (5 \times 5)} = 5\sqrt{3}\)

Simplifying radicals with variables involves applying the same principles used for simplifying numerical radicals, with additional consideration for the variables. Here are the steps to follow:

1. Identify the prime factorization: Write the expression under the radical as a product of its prime factors, including the variables.

   Example: \( \sqrt{100x^4y^6z^3} = \sqrt{2 \times 2 \times 5 \times 5 \times x \times x \times x \times x \times y \times y \times y \times y \times y \times y \times z \times z \times z} \)

2. Group the factors in pairs: Combine the factors in pairs of identical factors.

   Example: \( \sqrt{2^2 \times 5^2 \times x^2 \times x^2 \times y^2 \times y^2 \times y^2 \times z^2 \times z} \)

3. Simplify the radical: Bring out the factors that have pairs, while keeping in mind that \( \sqrt{x^2} = x \) when \( x \) is non-negative.

   Example: \( \sqrt{100x^4y^6z^3} = 2 \times 5 \times x^2 \times y^3 \times z \times \sqrt{z} = 10x^2y^3z\sqrt{z} \)

Here are additional examples:

1. Example 1: Simplify \( \sqrt{27x^3} \)

   Solution:

   • Factorize: \( \sqrt{3^3 \times x^3} \)
   • Simplify: \( \sqrt{3^3} \times \sqrt{x^3} = 3 \times x \times \sqrt{3} \times \sqrt{x} = 3x\sqrt{3x} \)

2. Example 2: Simplify \( \sqrt{16y^4} \)

   Solution:

   • Factorize: \( \sqrt{2^4 \times y^4} \)
   • Simplify: \( \sqrt{2^4} \times \sqrt{y^4} = 2^2 \times y^2 = 4y^2 \)

Remember the following rules for simplifying radical expressions:

• \( \sqrt{ab} = \sqrt{a} \times \sqrt{b} \)
• \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) for \( b \neq 0 \)
• \( \sqrt{a + b} \neq \sqrt{a} + \sqrt{b} \)
• \( \sqrt{a - b} \neq \sqrt{a} - \sqrt{b} \)

When simplifying radical fractions, the goal is to remove the radical from the denominator. This process is known as rationalizing the denominator. Here are the steps to simplify radical fractions:

1. Identify the radical fraction: A typical radical fraction looks like $$
   
   1
   
   3
   
   
   .

2. Multiply the numerator and the denominator by the radical in the denominator: This helps eliminate the radical in the denominator. For example:

   $\frac{1}{\sqrt{3}}\times \frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{3}}{3}$

3. Simplify the expression: Ensure the fraction is in its simplest form. In our example, the result $$
   
   
   3
   
   3
   
   is already simplified.

4. Handle complex denominators: If the denominator is a binomial involving radicals, use the conjugate to rationalize. For example, for a fraction like $$
   
   1
   
   1
   +
   
   2
   
   
   
   , multiply by the conjugate $$
   
   1
   -
   
   2
   
   
   :

   $\frac{1}{1+\sqrt{2}}\times \frac{1-\sqrt{2}}{1-\sqrt{2}}=\frac{1-\sqrt{2}}{-1}$

5. Finalize the simplified form: Simplify any remaining radicals and fractions to their lowest terms.

By following these steps, you can effectively simplify any radical fraction. Let's practice with more examples:

Example 1

Simplify $$

5

7

Multiply by $$


7


7


:

The simplified form is $$


5

7


7

.

Example 2

Simplify $$


3

2



2
+

5

Multiply by the conjugate $$

2
-

5


:

Simplify:

The simplified form is $$

-3

2

(
2
-

5

)

.

Adding and subtracting radicals is similar to combining like terms in algebra. Radicals can only be added or subtracted if they have the same radicand (the number under the radical) and the same index (the degree of the root).

Here are the steps to simplify sums and differences of radicals:

1. Simplify each radical expression separately. This involves factoring out perfect squares, cubes, etc., from the radicand.
2. Identify like radicals. Radicals are like terms if they have the same index and radicand.
3. Combine the coefficients of like radicals. The radical part remains unchanged.

Here are some examples to illustrate the process:

Example 1: Adding Like Radicals

Simplify \(2\sqrt{6} + 5\sqrt{6}\).

Since both terms have the same radicand (\(\sqrt{6}\)), we can combine them:

\[
2\sqrt{6} + 5\sqrt{6} = (2 + 5)\sqrt{6} = 7\sqrt{6}
\]

Example 2: Subtracting Like Radicals

Simplify \(4\sqrt{10} - 5\sqrt{10}\).

Since both terms have the same radicand (\(\sqrt{10}\)), we can combine them:

\[
4\sqrt{10} - 5\sqrt{10} = (4 - 5)\sqrt{10} = -\sqrt{10}
\]

Example 3: Combining Unlike Radicals

Simplify \(10\sqrt{5} + 6\sqrt{2} - 9\sqrt{5} - 7\sqrt{2}\).

First, combine the like radicals:

\[
10\sqrt{5} - 9\sqrt{5} + 6\sqrt{2} - 7\sqrt{2} = (10 - 9)\sqrt{5} + (6 - 7)\sqrt{2} = \sqrt{5} - \sqrt{2}
\]

Note that \(\sqrt{5}\) and \(\sqrt{2}\) are not like radicals, so they cannot be combined further.

Example 4: Combining Radicals with Different Indices

Simplify \(5\sqrt[3]{10} + 3\sqrt{10} - \sqrt[3]{10} - 2\sqrt{10}\).

Combine the like radicals separately:

\[
5\sqrt[3]{10} - \sqrt[3]{10} + 3\sqrt{10} - 2\sqrt{10} = (5 - 1)\sqrt[3]{10} + (3 - 2)\sqrt{10} = 4\sqrt[3]{10} + \sqrt{10}
\]

Since \(\sqrt[3]{10}\) and \(\sqrt{10}\) have different indices, they cannot be combined further.

By following these steps, you can simplify sums and differences of radical expressions efficiently. Remember, the key is to look for like radicals and combine their coefficients.

Simplifying the product of radicals involves using the property that the product of two radicals is equal to the radical of the product. Here are the steps to simplify the products of radicals:

1. Multiply the numbers inside the radicals.
2. Simplify the resulting radical expression if possible.

Let's look at some examples to illustrate this process:

Example 1

Simplify: \( \sqrt{2} \cdot \sqrt{8} \)

1. Multiply the radicands: \( \sqrt{2 \cdot 8} = \sqrt{16} \)
2. Simplify the radical: \( \sqrt{16} = 4 \)

Answer: \( 4 \)

Example 2

Simplify: \( \sqrt{3} \cdot \sqrt{12} \)

1. Multiply the radicands: \( \sqrt{3 \cdot 12} = \sqrt{36} \)
2. Simplify the radical: \( \sqrt{36} = 6 \)

Answer: \( 6 \)

Example 3

Simplify: \( \sqrt{5} \cdot \sqrt{20} \)

1. Multiply the radicands: \( \sqrt{5 \cdot 20} = \sqrt{100} \)
2. Simplify the radical: \( \sqrt{100} = 10 \)

Answer: \( 10 \)

Example 4 (with variables)

Simplify: \( \sqrt{4x} \cdot \sqrt{5x^3} \)

1. Multiply the radicands: \( \sqrt{4x \cdot 5x^3} = \sqrt{20x^4} \)
2. Simplify the radical: \[ \sqrt{20x^4} = \sqrt{4 \cdot 5 \cdot x^4} = \sqrt{4} \cdot \sqrt{5} \cdot \sqrt{x^4} = 2 \cdot \sqrt{5} \cdot x^2 = 2x^2\sqrt{5} \]

Answer: \( 2x^2\sqrt{5} \)

Example 5

Simplify: \( \sqrt{6} \cdot \sqrt{24} \)

1. Multiply the radicands: \( \sqrt{6 \cdot 24} = \sqrt{144} \)
2. Simplify the radical: \( \sqrt{144} = 12 \)

Answer: \( 12 \)

Using these steps, you can simplify any product of radicals, whether they contain just numbers or include variables.

Rationalizing the denominator involves eliminating radicals from the denominator of a fraction. This is achieved by multiplying the numerator and denominator by a suitable radical that will make the denominator a rational number. Here are the steps to rationalize different types of denominators:

1. Rationalizing a Denominator with a Single Radical

For a fraction with a single radical in the denominator:

1. Identify the radical in the denominator.
2. Multiply the numerator and the denominator by the same radical.
3. Simplify the expression if possible.

Example:

\(\frac{1}{\sqrt{2}}\)

Multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\):

\(\frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}\)

2. Rationalizing a Denominator with a Binomial Radical

For a fraction with a binomial radical in the denominator:

1. Identify the conjugate of the denominator. The conjugate of \(a + \sqrt{b}\) is \(a - \sqrt{b}\), and vice versa.
2. Multiply the numerator and the denominator by the conjugate of the denominator.
3. Simplify the expression using the difference of squares formula.

Example:

\(\frac{3}{2 + \sqrt{3}}\)

Conjugate: \(2 - \sqrt{3}\)

Multiply by \(\frac{2 - \sqrt{3}}{2 - \sqrt{3}}\):

\(\frac{3(2 - \sqrt{3})}{(2 + \sqrt{3})(2 - \sqrt{3})} = \frac{3(2 - \sqrt{3})}{4 - 3} = 3(2 - \sqrt{3}) = 6 - 3\sqrt{3}\)

3. Rationalizing Complex Radical Denominators

For more complex denominators involving multiple radicals or higher roots, follow similar steps, but ensure that the radicals multiply to form a perfect square or higher power.

Example:

\(\frac{3\sqrt[4]{11}}{\sqrt[4]{2}}\)

Multiply by \(\frac{\sqrt[4]{8}}{\sqrt[4]{8}}\):

\(\frac{3\sqrt[4]{11} \cdot \sqrt[4]{8}}{\sqrt[4]{2} \cdot \sqrt[4]{8}} = \frac{3\sqrt[4]{88}}{\sqrt[4]{16}} = \frac{3\sqrt[4]{88}}{2}\)

4. Rationalizing with a Difference of Radicals

For denominators that involve a difference or sum of radicals:

Example:

\(\frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} + \sqrt{2}}\)

Conjugate: \(\sqrt{6} - \sqrt{2}\)

Multiply by \(\frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} - \sqrt{2}}\):

\(\frac{(\sqrt{6} - \sqrt{2})^2}{(\sqrt{6} + \sqrt{2})(\sqrt{6} - \sqrt{2})} = \frac{6 - 2\sqrt{12} + 2}{6 - 2} = \frac{6 - 4\sqrt{3} + 2}{4} = \frac{8 - 4\sqrt{3}}{4} = 2 - \sqrt{3}\)

By following these steps, you can effectively rationalize any denominator containing radicals, ensuring your final expression is simpler and more elegant.

Simplifying complex radicals involves several steps to ensure the expression is as simple as possible. Here are detailed steps and examples to help you understand the process:

1. Identify and Separate the Radicals:

   Consider the expression \(\sqrt{72a^5b^6}\). First, separate the expression into its prime factors and variables:

   \[\sqrt{72a^5b^6} = \sqrt{(2^3 \cdot 3^2) \cdot a^5 \cdot b^6}\]

2. Apply the Product Rule:

   Using the product rule for radicals, \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\), separate the factors under the radical:

   \[\sqrt{72a^5b^6} = \sqrt{2^3} \cdot \sqrt{3^2} \cdot \sqrt{a^5} \cdot \sqrt{b^6}\]

3. Simplify Each Radical:

   • \(\sqrt{2^3} = \sqrt{2^2 \cdot 2} = 2\sqrt{2}\)
   • \(\sqrt{3^2} = 3\)
   • \(\sqrt{a^5} = \sqrt{a^4 \cdot a} = a^2\sqrt{a}\)
   • \(\sqrt{b^6} = \sqrt{(b^3)^2} = b^3\)

4. Combine the Simplified Parts:

   Now, multiply all the simplified parts together:

   \[2\sqrt{2} \cdot 3 \cdot a^2\sqrt{a} \cdot b^3 = 6a^2b^3\sqrt{2a}\]

So, the simplified form of \(\sqrt{72a^5b^6}\) is \(6a^2b^3\sqrt{2a}\).

Let's look at another example for further clarity:

1. Example 2: Simplify \(\sqrt[3]{54x^4y^5}\).

   • First, factor inside the radical: \(54 = 2 \cdot 3^3\).
   • Rewrite the expression: \(\sqrt[3]{54x^4y^5} = \sqrt[3]{2 \cdot 3^3 \cdot x^4 \cdot y^5}\).
   • Separate the factors: \(\sqrt[3]{2} \cdot \sqrt[3]{3^3} \cdot \sqrt[3]{x^4} \cdot \sqrt[3]{y^5}\).
   • Simplify each term:
     • \(\sqrt[3]{2}\) remains as is because 2 is not a perfect cube.
     • \(\sqrt[3]{3^3} = 3\).
     • \(\sqrt[3]{x^4} = x^{4/3} = x^{1 + 1/3} = x \cdot \sqrt[3]{x}\).
     • \(\sqrt[3]{y^5} = y^{5/3} = y^{1 + 2/3} = y \cdot \sqrt[3]{y^2}\).
   • Combine the simplified parts: \(3x y \sqrt[3]{2x y^2}\).

Therefore, the simplified form of \(\sqrt[3]{54x^4y^5}\) is \(3x y \sqrt[3]{2x y^2}\).

Simplifying radical expressions can sometimes involve special cases that require particular attention. Below are some special cases and the methods to simplify them:

Simplifying Radicals Involving Perfect Squares and Cubes

When the radicand (the number inside the radical) is a perfect square or cube, the radical can be simplified directly.

• Example: \(\sqrt{36} = 6\), because \(36\) is a perfect square.
• Example: \(\sqrt[3]{27} = 3\), because \(27\) is a perfect cube.

Simplifying Radicals Involving Variables

Radicals involving variables follow similar rules. If the exponent of the variable is a multiple of the index of the radical, it can be simplified.

• Example: \(\sqrt{x^4} = x^2\), because \(4\) is a multiple of \(2\).
• Example: \(\sqrt[3]{y^6} = y^2\), because \(6\) is a multiple of \(3\).

Simplifying Radicals with Absolute Values

When simplifying radicals with even indices (such as square roots) involving variables, use absolute values to ensure the result is non-negative.

• Example: \(\sqrt{x^2} = |x|\), because the square root of \(x^2\) is the absolute value of \(x\).

Radicals in the Denominator

Rationalizing the denominator involves eliminating radicals from the denominator of a fraction by multiplying the numerator and the denominator by a suitable radical.

• Example: \(\frac{1}{\sqrt{2}} = \frac{1 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{\sqrt{2}}{2}\)

Simplifying Sum and Difference of Radicals

Only like radicals (radicals with the same radicand and index) can be combined by addition or subtraction.

• Example: \(\sqrt{3} + 2\sqrt{3} = 3\sqrt{3}\)
• Example: \(\sqrt{5} - \sqrt{2}\) cannot be simplified further as the radicands are different.

Combining Radicals with Different Indices

To simplify radicals with different indices, rewrite the radicals as expressions with rational exponents, find a common denominator, and then combine them.

• Example: \(\sqrt{a} \cdot \sqrt[3]{b} = a^{1/2} \cdot b^{1/3}\)
• Rewrite with a common exponent: \(a^{3/6} \cdot b^{2/6} = (a^3 b^2)^{1/6}\)

Complex Radical Expressions

Complex expressions may require multiple steps to simplify, including using the properties of exponents and the distributive property.

• Example: Simplify \(\sqrt{50x^2} = \sqrt{25 \cdot 2 \cdot x^2} = 5x\sqrt{2}\).

By recognizing these special cases, you can efficiently simplify a wide range of radical expressions.

When simplifying radical expressions, students often make common mistakes. Here are some of these mistakes and how to avoid them:

• Incorrect Factorization of the Radicand:

  One common mistake is incorrectly rewriting the number under the square root sign as a product of any two factors, instead of using a perfect square factor.

  For example, simplifying $$
  
  48
  
  as $$
  
  6
  
  ×
  
  8
  
  is incorrect. The correct factorization is $$
  
  16
  
  ×
  
  3
  
  , which simplifies to $$
  4
  
  3
  
  .

• Not Simplifying Fully:

  Another common mistake is stopping too early and not fully simplifying the radical expression.

  For example, simplifying $$
  
  32
  
  =
  2
  
  8
  
  instead of fully simplifying to $$
  4
  
  2
  
  .

• Incorrect Simplification of Variable Expressions:

  When simplifying radicals with variables, ensure the exponents are handled correctly.

  For example, thinking that $$
  
  
  x
  9
  
  
  =
  
  x
  3
  
  is incorrect. The correct simplification is $$
  
  x
  
  ×
  
  
  x
  8
  
  
  =
  
  x
  4
  
  
  x
  
  .

• Misinterpreting the Product Rule:

  The product rule of square roots states that $$
  
  (
  a
  ×
  b
  )
  
  =
  
  a
  
  ×
  
  b
  
  , where both $$
  a
  and $$
  b
  are greater than 0. Misinterpreting this rule can lead to errors.

  For example, incorrectly simplifying $$
  
  72
  
  =
  
  8
  
  ×
  
  9
  
  =
  3
  
  8
  
  instead of the correct simplification $$
  
  36
  
  ×
  
  2
  
  =
  6
  
  2
  .
  

• Ignoring Rationalizing the Denominator:

  When an expression has a radical in the denominator, it should be rationalized by multiplying both the numerator and the denominator by a suitable term to remove the radical from the denominator.

  For example, simplifying $$
  
  3
  (
  2
  +
  
  2
  
  )
  
  involves multiplying both the numerator and the denominator by $$
  (
  2
  −
  
  2
  
  )
  to obtain $$
  
  
  3
  (
  2
  −
  
  2
  
  )
  
  2
  .
  .

Here are some practice problems to help you master simplifying radical expressions. Each problem is followed by a detailed solution to guide you through the process.

1. Simplify \( \sqrt{72} \).

   Solution:

   1. Find the largest perfect square factor of 72. The factors of 72 include 4, 9, and 36. The largest is 36.
   2. Rewrite \( 72 \) as a product of \( 36 \) and another factor: \( 72 = 36 \times 2 \).
   3. Use the product rule of square roots: \( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} \).
   4. Simplify the square root of 36: \( \sqrt{36} = 6 \).
   5. Combine the results: \( \sqrt{72} = 6\sqrt{2} \).

2. Simplify \( \sqrt{50} \).

   Solution:

   1. Find the largest perfect square factor of 50. The largest perfect square factor is 25.
   2. Rewrite \( 50 \) as a product of \( 25 \) and another factor: \( 50 = 25 \times 2 \).
   3. Use the product rule of square roots: \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} \).
   4. Simplify the square root of 25: \( \sqrt{25} = 5 \).
   5. Combine the results: \( \sqrt{50} = 5\sqrt{2} \).

3. Simplify \( \sqrt{128} \).

   Solution:

   1. Find the largest perfect square factor of 128. The largest perfect square factor is 64.
   2. Rewrite \( 128 \) as a product of \( 64 \) and another factor: \( 128 = 64 \times 2 \).
   3. Use the product rule of square roots: \( \sqrt{128} = \sqrt{64 \times 2} = \sqrt{64} \times \sqrt{2} \).
   4. Simplify the square root of 64: \( \sqrt{64} = 8 \).
   5. Combine the results: \( \sqrt{128} = 8\sqrt{2} \).

4. Simplify \( \sqrt{18x^4y^6} \).

   Solution:

   1. Break down the numerical part: \( 18 = 9 \times 2 \).
   2. Simplify the variable part: \( x^4 \) and \( y^6 \) are already perfect squares.
   3. Use the product rule: \( \sqrt{18x^4y^6} = \sqrt{9 \times 2 \times x^4 \times y^6} = \sqrt{9} \times \sqrt{2} \times \sqrt{x^4} \times \sqrt{y^6} \).
   4. Simplify each part: \( \sqrt{9} = 3 \), \( \sqrt{x^4} = x^2 \), \( \sqrt{y^6} = y^3 \).
   5. Combine the results: \( \sqrt{18x^4y^6} = 3x^2y^3\sqrt{2} \).

5. Simplify \( \sqrt{75a^8b^3} \).

   Solution:

   1. Break down the numerical part: \( 75 = 25 \times 3 \).
   2. Simplify the variable part: \( a^8 \) and \( b^3 \) (note \( b^3 \) needs to be further simplified).
   3. Use the product rule: \( \sqrt{75a^8b^3} = \sqrt{25 \times 3 \times a^8 \times b^3} = \sqrt{25} \times \sqrt{3} \times \sqrt{a^8} \times \sqrt{b^3} \).
   4. Simplify each part: \( \sqrt{25} = 5 \), \( \sqrt{a^8} = a^4 \), and \( \sqrt{b^3} = b^{1.5} = b\sqrt{b} \).
   5. Combine the results: \( \sqrt{75a^8b^3} = 5a^4b\sqrt{3b} \).

In this section, we will explore advanced techniques for simplifying radical expressions. These techniques are useful when dealing with more complex expressions involving higher-order roots, variables with large exponents, and expressions requiring rationalization. Let’s delve into some advanced methods step-by-step.

1. Higher-Order Roots

When simplifying higher-order roots, such as cube roots or fourth roots, the same principles apply as with square roots. We look for the largest perfect power that divides the radicand.

1. Example: Simplify \( \sqrt[3]{24} \).
2. Step 1: Identify the largest perfect cube that divides 24. In this case, it is 8.
3. Step 2: Express 24 as a product of 8 and 3: \( 24 = 8 \times 3 \).
4. Step 3: Apply the product rule: \[ \sqrt[3]{24} = \sqrt[3]{8 \times 3} = \sqrt[3]{8} \times \sqrt[3]{3} = 2\sqrt[3]{3} \]

2. Simplifying Radicals with Variables

When simplifying radicals involving variables, factor the variable terms into pairs (for square roots) or groups corresponding to the root's order.

1. Example: Simplify \( \sqrt{a^6 b^4 c^5} \).
2. Step 1: Break down each variable's exponent into pairs: \[ a^6 = (a^3)^2, \quad b^4 = (b^2)^2, \quad c^5 = (c^2)^2 \cdot c \]
3. Step 2: Simplify each part: \[ \sqrt{a^6 b^4 c^5} = \sqrt{(a^3)^2 \cdot (b^2)^2 \cdot (c^2)^2 \cdot c} = a^3 b^2 c^2 \sqrt{c} \]

3. Rationalizing the Denominator

Rationalizing the denominator involves eliminating radicals from the denominator of a fraction. For higher-order roots, multiply the numerator and denominator by a term that will result in a perfect power in the denominator.

1. Example: Rationalize \( \frac{1}{\sqrt[3]{4}} \).
2. Step 1: Identify a term that, when multiplied by \( \sqrt[3]{4} \), results in a perfect cube. Here, multiply by \( \sqrt[3]{16} \): \[ \frac{1}{\sqrt[3]{4}} \times \frac{\sqrt[3]{16}}{\sqrt[3]{16}} = \frac{\sqrt[3]{16}}{\sqrt[3]{64}} = \frac{\sqrt[3]{16}}{4} \]

4. Combining Like Radicals

Combining like radicals involves simplifying expressions with the same radicand. Only radicals with the same index and radicand can be combined.

1. Example: Simplify \( 2\sqrt{3} + 5\sqrt{3} \).
2. Step 1: Combine coefficients of like radicals: \[ 2\sqrt{3} + 5\sqrt{3} = (2 + 5)\sqrt{3} = 7\sqrt{3} \]

5. Using Conjugates for Rationalization

When the denominator is a binomial involving radicals, multiply by the conjugate to rationalize.

1. Example: Rationalize \( \frac{1}{1 + \sqrt{2}} \).
2. Step 1: Multiply the numerator and denominator by the conjugate \( 1 - \sqrt{2} \): \[ \frac{1}{1 + \sqrt{2}} \times \frac{1 - \sqrt{2}}{1 - \sqrt{2}} = \frac{1 - \sqrt{2}}{1 - (\sqrt{2})^2} = \frac{1 - \sqrt{2}}{1 - 2} = \frac{1 - \sqrt{2}}{-1} = -1 + \sqrt{2} \]

By mastering these advanced techniques, you can simplify a wide range of radical expressions more efficiently and accurately.

Simplifying radical expressions is not just a theoretical exercise; it has numerous practical applications across various fields. Here, we will explore some of the key areas where radical simplification is essential.

1. Engineering and Physics

In engineering and physics, radical simplification is frequently used to simplify complex formulas and equations, making them easier to solve and interpret. For example, when dealing with quadratic equations that describe motion, electrical circuits, or wave functions, simplifying the radicals can help in finding precise solutions efficiently.

Consider the equation for the period of a pendulum:

$$ T = 2\pi\sqrt{\frac{L}{g}} $$

By simplifying the radical, engineers can more easily manipulate and apply this formula in different contexts.

2. Architecture and Construction

Architects and construction engineers use radical simplification to handle measurements and calculations related to structures. For example, when working with the Pythagorean theorem to determine distances and angles in building plans:

$$ c = \sqrt{a^2 + b^2} $$

Simplifying the radicals helps in providing clear and accurate measurements, which are crucial for ensuring the stability and safety of structures.

3. Computer Graphics and Animation

In computer graphics, simplifying radical expressions can enhance the performance of rendering algorithms. For instance, calculating distances and transformations in 3D space often involves square roots. Simplifying these expressions helps in optimizing the code for faster execution.

Consider the distance formula in 3D space:

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} $$

By simplifying the radicals, developers can improve the efficiency of graphics processing.

4. Finance and Economics

In finance, radical simplification is used in various models to predict economic trends and evaluate financial products. For example, in the Black-Scholes model for option pricing, radicals appear in the formula for the standard deviation of stock prices. Simplifying these expressions helps in making more accurate financial predictions and decisions.

Consider the volatility formula:

$$ \sigma = \sqrt{\frac{1}{T}\sum_{i=1}^T (R_i - \bar{R})^2} $$

Simplifying this radical expression is crucial for accurate financial analysis and risk assessment.

5. Data Science and Machine Learning

In data science and machine learning, simplifying radical expressions can improve the efficiency of algorithms. For example, in clustering algorithms like K-means, calculating Euclidean distances involves square roots. Simplifying these calculations can lead to faster convergence and more efficient data processing.

Consider the Euclidean distance formula:

$$ d = \sqrt{\sum_{i=1}^n (x_i - y_i)^2} $$

By simplifying the radical expressions, data scientists can optimize their algorithms for better performance.

These applications illustrate the importance of mastering radical simplification techniques. Whether you are an engineer, architect, computer scientist, financial analyst, or data scientist, being proficient in simplifying radicals can significantly enhance your problem-solving skills and efficiency.

In this comprehensive guide, we've covered various aspects of simplifying radical expressions. Let's summarize the key points:

• Introduction to Radical Expressions: We started with understanding what radical expressions are and their basic components.
• Basic Concepts of Radicals: We explored the properties and rules of radicals, such as the product and quotient rules.
• Prime Factorization and Radicals: We discussed the importance of prime factorization in simplifying radicals and practiced with examples.
• Simplifying Single Radical Expressions: We learned how to simplify radicals by finding the largest perfect square factors and using prime factorization.
• Simplifying Radicals with Variables: We extended our knowledge to include variables in radical expressions and applied the same rules for simplification.
• Simplifying Radical Fractions: We tackled radicals in the numerator and denominator, using techniques like rationalizing the denominator.
• Simplifying Sum and Difference of Radicals: We practiced combining like terms in radical expressions.
• Simplifying Products of Radicals: We applied the product rule to simplify expressions involving the product of two or more radicals.
• Rationalizing the Denominator: We learned methods to eliminate radicals from the denominator by multiplying by the conjugate.
• Complex Radicals Simplification: We explored more complex examples involving multiple steps of simplification.
• Special Cases in Radical Simplification: We looked at unique scenarios and how to handle them.
• Common Mistakes and How to Avoid Them: We identified typical errors in simplifying radicals and provided strategies to prevent them.
• Practice Problems with Solutions: We reinforced learning with a variety of practice problems, offering detailed solutions for better understanding.
• Advanced Techniques in Radical Simplification: We delved into more advanced methods and tips for simplifying radical expressions efficiently.
• Applications of Radical Simplification: We explored real-world applications where simplifying radicals is useful.

By mastering these concepts, you can confidently simplify radical expressions in various mathematical contexts. Remember to practice regularly and review these key points to reinforce your understanding. Simplifying radicals is a fundamental skill that will aid you in advanced mathematical studies and practical applications alike.