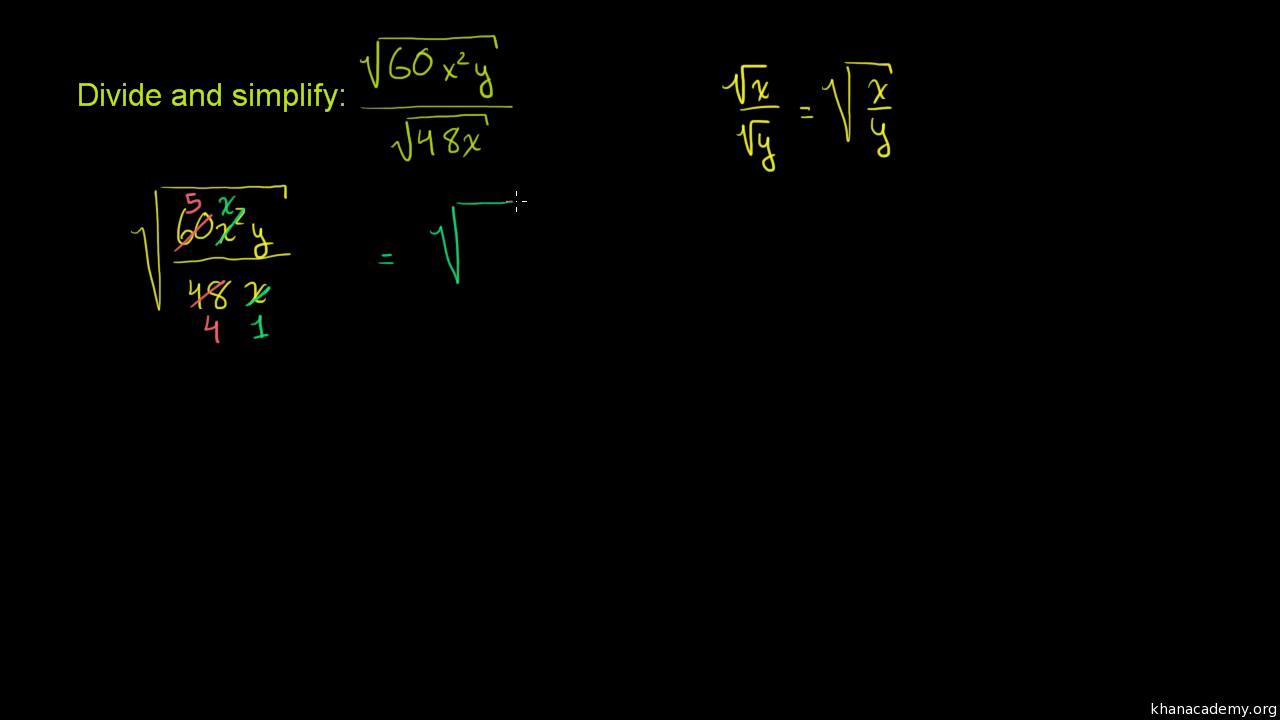Topic how to simplify radical expressions with variables: Unlock the secrets to simplifying radical expressions with variables! This guide will walk you through the essential steps, techniques, and tips to master this fundamental algebra skill. Learn how to handle different exponents, combine like terms, and apply rules for radicals effectively. Dive in and enhance your mathematical understanding with clear examples and practical advice.
Table of Content
- Simplifying Radical Expressions with Variables
- Introduction to Radical Expressions
- Understanding Radicals and Exponents
- Basic Rules for Simplifying Radical Expressions
- Prime Factorization Method
- Simplifying Radicals with Numerical Coefficients
- Combining Like Terms Under the Radical
- Product Rule of Square Roots
- Quotient Rule of Square Roots
- Simplifying Radicals with Variables
- Even and Odd Exponents
- Simplifying Expressions with Multiple Variables
- Using Absolute Values in Radical Simplification
- Examples of Simplifying Radical Expressions
- Advanced Techniques and Tips
- Common Mistakes to Avoid
- Practice Problems and Solutions
- Conclusion
- YOUTUBE: Hướng dẫn đơn giản hóa biểu thức căn với biến số, số mũ, phân số, căn bậc ba trong đại số. Phù hợp cho người học muốn nắm vững kiến thức cơ bản và nâng cao.
Simplifying Radical Expressions with Variables
To simplify radical expressions with variables, follow these steps:
Steps for Simplifying Radical Expressions
- Write the number under the radical as a product of its prime factors and expand the variables.
- Combine the factors in pairs of identical factors.
- Bring out the factors with powers of 2 out of the radical.
- Simplify the radical until no further simplification can be done.
Example 1: Simplify \(\sqrt{x^{10}}\)
\[
\sqrt{x^{10}} = x^5
\]
Since the exponent is even, we take half of the exponent to simplify.
Example 2: Simplify \(\sqrt{y^9}\)
\[
\sqrt{y^9} = y^4 \sqrt{y}
\]
Since the exponent is odd, we subtract 1 from the exponent and rewrite the expression as a product, then simplify.
Example 3: Simplify \(\sqrt{x^6 y^3}\)
\[
\sqrt{x^6 y^3} = x^3 y \sqrt{y}
\]
Here, \(x^6\) has an even exponent, so it is straightforward. For \(y^3\), we separate it into \(y^2\) and \(y\) and then simplify.
Rules for Simplifying Radical Expressions
- \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), \(b \neq 0\)
- \(\sqrt{a} + \sqrt{b} \neq \sqrt{a + b}\)
- \(\sqrt{a} - \sqrt{b} \neq \sqrt{a - b}\)
Example 4: Simplify \(\sqrt{12x^2y^4}\)
\[
\sqrt{12x^2y^4} = 2xy^2\sqrt{3}
\]
Prime factorize 12 and break down the variables into pairs to simplify.
Example 5: Simplify \(\sqrt{54a^{10}b^{16}c^7}\)
\[
\sqrt{54a^{10}b^{16}c^7} = 3a^5b^8c^3\sqrt{6c}
\]
Group the variables into pairs and simplify step-by-step.
Tips and Tricks
- To simplify radicals in the denominator, multiply by the conjugate.
- Remember, the square root of a number is always non-negative.
Example 6: Simplify \(\frac{\sqrt{12}}{\sqrt{5}}\)
\[
\frac{\sqrt{12}}{\sqrt{5}} = \frac{2\sqrt{15}}{5}
\]
Multiply the numerator and the denominator by \(\sqrt{5}\) to simplify.
Example 7: Simplify \(\frac{10b^2c^2}{c\sqrt{4b^3}}\)
\[
\frac{10b^2c^2}{c\sqrt{4b^3}} = 5c\sqrt{b}
\]
Rationalize the denominator and simplify.

READ MORE:
Introduction to Radical Expressions
Radical expressions involve roots, such as square roots or cube roots, of numbers or variables. Simplifying these expressions is a fundamental skill in algebra, as it helps in solving equations and understanding more complex mathematical concepts.
A radical expression is generally written as \( \sqrt[n]{a} \), where \( n \) is the degree of the root and \( a \) is the radicand. For example, \( \sqrt{16} \) is a square root because the degree is 2 (usually omitted in notation), while \( \sqrt[3]{8} \) is a cube root.
Simplifying a radical expression means rewriting it in its simplest form so that there are no perfect square factors (for square roots), or generally, no perfect \( n \)-th power factors left under the radical. Here are the basic steps:
- Identify Perfect Powers: Check the radicand for any perfect squares (or cubes, etc., depending on the degree of the root). For instance, in \( \sqrt{72} \), the perfect square factors are 4 and 36.
- Rewrite the Radicand: Express the radicand as a product of these perfect powers and other factors. For \( \sqrt{72} \), this can be done as \( \sqrt{36 \times 2} \).
- Apply the Product Rule: Use the property \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) to separate the radical into simpler parts. Thus, \( \sqrt{36 \times 2} = \sqrt{36} \cdot \sqrt{2} \).
- Simplify: Take the root of the perfect power and simplify the expression. \( \sqrt{36} \) is 6, so \( \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2} \).
Simplifying radicals with variables follows similar principles:
- Even Exponents: If the variable under the radical has an even exponent, it can be divided by the degree of the root. For example, \( \sqrt{x^4} = x^2 \).
- Odd Exponents: For odd exponents, reduce the exponent by 1 to make it even, and then factor out the remaining variable. For example, \( \sqrt{x^5} = \sqrt{x^4 \cdot x} = x^2 \sqrt{x} \).
Using these techniques ensures that radical expressions are simplified correctly, making further algebraic manipulation more straightforward.
Understanding Radicals and Exponents
Radicals, often referred to as roots, are expressions that involve the root of a number. The most common type is the square root, but higher-order roots such as cube roots also exist. Exponents, on the other hand, are shorthand notation for repeated multiplication of the same number. Understanding the relationship between radicals and exponents is crucial for simplifying radical expressions.
A radical expression can be written in terms of exponents. For instance, the square root of a number \(a\) can be written as \(a^{1/2}\), and the \(n\)-th root of \(a\) can be written as \(a^{1/n}\).
Here are some important properties and rules to remember:
- Product Rule: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Rule: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) (for \(b \neq 0\))
- Power Rule: \((a^m)^n = a^{m \cdot n}\)
When simplifying radical expressions with variables, the same rules apply. Consider the following steps:
- Rewrite the expression: Express the radicand (the number inside the radical) as a product of its prime factors.
- Use the product rule: Apply the product rule of radicals to separate the expression into simpler parts.
- Simplify the variables: If the exponent of a variable is even, take half of the exponent. If it's odd, reduce it by one to make it even and then take half of the exponent.
Here are some examples:
| Expression | Step-by-Step Simplification |
|---|---|
| \(\sqrt{x^{10}}\) |
1. The exponent 10 is even. 2. Take half of 10. 3. \(\sqrt{x^{10}} = x^{10/2} = x^5\) |
| \(\sqrt{y^9}\) |
1. The exponent 9 is odd. 2. Rewrite \(y^9\) as \(y^1 \cdot y^8\). 3. Simplify \(y^8\) since 8 is even. 4. \(\sqrt{y^9} = \sqrt{y^1 \cdot y^8} = \sqrt{y} \cdot \sqrt{y^8} = y^4 \sqrt{y}\) |
| \(\sqrt{x^6 y^3}\) |
1. Separate the variables. 2. \(\sqrt{x^6 y^3} = \sqrt{x^6} \cdot \sqrt{y^3}\) 3. Simplify each part: \(x^6\) is even, \(y^3\) is odd. 4. \(\sqrt{x^6} = x^3\) 5. Rewrite \(y^3\) as \(y^2 \cdot y\). 6. \(\sqrt{y^3} = \sqrt{y^2 \cdot y} = y \sqrt{y}\) 7. Combine: \(\sqrt{x^6 y^3} = x^3 \cdot y \sqrt{y} = x^3 y \sqrt{y}\) |
By following these steps and using the rules of exponents and radicals, you can simplify complex radical expressions involving variables.
Basic Rules for Simplifying Radical Expressions
Radical expressions can often be simplified using a few fundamental rules. Here are the basic steps and rules to simplify radical expressions:
- Product Rule: The square root of a product is the product of the square roots. For any non-negative numbers \(a\) and \(b\): \[ \sqrt{ab} = \sqrt{a} \cdot \sqrt{b} \]
- Quotient Rule: The square root of a quotient is the quotient of the square roots. For any non-negative numbers \(a\) and \(b\), with \(b \neq 0\): \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
- Simplifying Radicals with Perfect Squares: To simplify a radical, look for perfect square factors of the radicand (the number inside the radical). For example: \[ \sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2} \]
- Combining Like Terms: Radicals with the same radicand can be combined. For example: \[ 2\sqrt{3} + 5\sqrt{3} = 7\sqrt{3} \]
- Simplifying Radicals with Variables: When variables are involved, apply the same rules. For even exponents, take the square root by dividing the exponent by 2: \[ \sqrt{x^6} = x^3 \] For odd exponents, separate one variable and apply the rule to the remaining even exponent: \[ \sqrt{x^7} = \sqrt{x^6 \cdot x} = x^3\sqrt{x} \]
- Using Prime Factorization: Break down the radicand into its prime factors to simplify. For example: \[ \sqrt{200} = \sqrt{2^3 \cdot 5^2} = \sqrt{2^2 \cdot 5^2 \cdot 2} = 10\sqrt{2} \]
Let's look at a detailed example:
Example
Simplify \(\sqrt{48x^4y^3}\)
- Factor the radicand into prime factors: \[ 48 = 2^4 \cdot 3, \quad x^4, \quad y^3 = y^2 \cdot y \]
- Apply the product rule: \[ \sqrt{48x^4y^3} = \sqrt{2^4 \cdot 3 \cdot x^4 \cdot y^2 \cdot y} \]
- Simplify each factor: \[ = \sqrt{2^4} \cdot \sqrt{3} \cdot \sqrt{x^4} \cdot \sqrt{y^2} \cdot \sqrt{y} \]
- Take the square root of each perfect square: \[ = 2^2 \cdot \sqrt{3} \cdot x^2 \cdot y \cdot \sqrt{y} \]
- Combine like terms: \[ = 4x^2y\sqrt{3y} \]
The simplified form is \(4x^2y\sqrt{3y}\).
Prime Factorization Method
The prime factorization method is an effective way to simplify radical expressions. This method involves breaking down the number under the radical sign into its prime factors and then simplifying based on those factors.
Here's a step-by-step guide on how to use the prime factorization method:
- Identify the number under the radical sign and write it as a product of its prime factors.
- Group the prime factors into pairs if dealing with square roots, or triplets for cube roots, etc.
- Simplify the expression by taking the root of the grouped factors.
- Multiply any remaining prime factors that are not paired or grouped.
Let's see some examples to understand this process better:
Example 1: Simplifying \(\sqrt{72}\)
- Prime factorize 72:
\(72 = 2 \times 2 \times 2 \times 3 \times 3\) - Group the factors into pairs:
\((2 \times 2) \times (3 \times 3) \times 2\) - Simplify:
\(\sqrt{72} = \sqrt{(2^2) \times (3^2) \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Example 2: Simplifying \(\sqrt[3]{54}\)
- Prime factorize 54:
\(54 = 2 \times 3 \times 3 \times 3\) - Group the factors into triplets:
\(3^3 \times 2\) - Simplify:
\(\sqrt[3]{54} = \sqrt[3]{(3^3) \times 2} = 3 \sqrt[3]{2}\)
Using the prime factorization method makes it easier to handle larger numbers and ensure accuracy in simplifying radical expressions. This technique is especially useful when dealing with variables.
Example 3: Simplifying \(\sqrt{x^12}\)
- Prime factorize the exponent:
\(x^{12}\) is already in its prime form. - Group the factors into pairs:
\(x^{12} = (x^6)^2\) - Simplify:
\(\sqrt{x^{12}} = x^6\)
For radicals with variables, the process is similar:
Example 4: Simplifying \(\sqrt{x^8 y^5}\)
- Prime factorize the exponents:
\(x^8\) and \(y^5\). - Group the factors:
\(x^8 = (x^4)^2\) and \(y^5 = y^4 \times y\). - Simplify:
\(\sqrt{x^8 y^5} = \sqrt{(x^4)^2 \times y^4 \times y} = x^4 y^2 \sqrt{y}\).
By following these steps, you can systematically simplify any radical expression using the prime factorization method.

Simplifying Radicals with Numerical Coefficients
When simplifying radicals with numerical coefficients, follow these detailed steps to ensure accuracy and clarity:
-
Identify the largest perfect square factor:
Find the largest perfect square that can divide the number under the radical (the radicand). This step is crucial for simplifying the expression effectively.
Example: For \(\sqrt{50}\), the largest perfect square factor is 25.
-
Rewrite the radical:
Express the radicand as a product of the perfect square and its corresponding factor.
Example: \(\sqrt{50} = \sqrt{25 \cdot 2}\)
-
Simplify the radical:
Take the square root of the perfect square factor and multiply it by the remaining factor under the radical.
Example: \(\sqrt{25 \cdot 2} = 5\sqrt{2}\)
-
Apply the coefficient:
If the radical expression has a numerical coefficient, multiply it by the simplified radical.
Example: \(3\sqrt{8}\)
- Find the largest perfect square factor of 8, which is 4.
- Rewrite the radical: \(3\sqrt{8} = 3\sqrt{4 \cdot 2}\)
- Simplify: \(3\sqrt{4 \cdot 2} = 3 \cdot 2\sqrt{2} = 6\sqrt{2}\)
By following these steps, you can simplify any radical expression with numerical coefficients. Let's consider a few more examples for clarity:
-
Example 1: Simplify \(2\sqrt{72}\)
- The largest perfect square factor of 72 is 36.
- Rewrite: \(2\sqrt{72} = 2\sqrt{36 \cdot 2}\)
- Simplify: \(2\sqrt{36 \cdot 2} = 2 \cdot 6\sqrt{2} = 12\sqrt{2}\)
-
Example 2: Simplify \(4\sqrt{98}\)
- The largest perfect square factor of 98 is 49.
- Rewrite: \(4\sqrt{98} = 4\sqrt{49 \cdot 2}\)
- Simplify: \(4\sqrt{49 \cdot 2} = 4 \cdot 7\sqrt{2} = 28\sqrt{2}\)
Practicing these steps with different numerical coefficients will help you master the process of simplifying radicals efficiently.
Combining Like Terms Under the Radical
When simplifying radical expressions, it's important to recognize and combine like terms under the radical. Like radicals have the same index and radicand. Here are the steps to combine like terms under the radical:
- Identify Like Radicals: Radicals are considered like radicals if they have the same index and the same radicand. For example, \(2\sqrt{6}\) and \(5\sqrt{6}\) are like radicals, whereas \(2\sqrt{6}\) and \(3\sqrt{5}\) are not.
- Combine the Coefficients: Once like radicals are identified, combine them by adding or subtracting their coefficients. The radical part remains unchanged. For example:
- \(2\sqrt{6} + 5\sqrt{6} = (2 + 5)\sqrt{6} = 7\sqrt{6}\)
- \(4\sqrt{10} - 5\sqrt{10} = (4 - 5)\sqrt{10} = -1\sqrt{10} = -\sqrt{10}\)
- Rearrange Terms: If there are multiple terms with different radicands, group like terms together for easier calculation. For instance:
- \(10\sqrt{5} + 6\sqrt{2} - 9\sqrt{5} - 7\sqrt{2}\)
- Group like terms: \((10\sqrt{5} - 9\sqrt{5}) + (6\sqrt{2} - 7\sqrt{2})\)
- Simplify: \(\sqrt{5} - \sqrt{2}\)
- Simplify the Radicals: Sometimes, the radicals may need to be simplified before combining. Simplify each radical by factoring out perfect squares:
- \(3\sqrt{32} - \sqrt{24} + \sqrt{32}\)
- Simplify: \(3(4\sqrt{2}) - \sqrt{4 \cdot 6} + 4\sqrt{2}\)
- Combine like terms: \(12\sqrt{2} - 2\sqrt{6} + 4\sqrt{2}\)
- Simplify: \(16\sqrt{2} - 2\sqrt{6}\)
- Variables Under the Radical: When variables are involved, ensure they are simplified similarly. Combine the coefficients and keep the variable part unchanged:
- \(3\sqrt{x} + \sqrt{x} = (3 + 1)\sqrt{x} = 4\sqrt{x}\)
Combining like terms under the radical simplifies the expression, making it easier to work with and understand. Remember, only like radicals can be combined; if the radicands or indices differ, they cannot be simplified further together.
Product Rule of Square Roots
The product rule of square roots is a fundamental property that allows us to simplify radical expressions by separating the radicand (the number inside the radical symbol) into its factors. The rule states that:
$$\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}$$
Here are the steps to simplify a radical expression using the product rule:
- Identify the factors: Find two factors of the radicand that can be used to split the expression.
- Apply the product rule: Separate the radicand into the product of the square roots of these factors.
- Simplify each square root: Simplify the individual square roots if possible.
- Combine the results: Multiply the simplified square roots to get the final simplified form.
Let's look at some examples to illustrate this:
- Example 1: Simplify \(\sqrt{72}\).
- Step 1: Identify the factors. \(72 = 36 \times 2\).
- Step 2: Apply the product rule. \(\sqrt{72} = \sqrt{36 \times 2}\).
- Step 3: Simplify each square root. \(\sqrt{36} = 6\) and \(\sqrt{2}\) remains as is.
- Step 4: Combine the results. \(\sqrt{72} = 6\sqrt{2}\).
- Example 2: Simplify \(\sqrt{48}\).
- Step 1: Identify the factors. \(48 = 16 \times 3\).
- Step 2: Apply the product rule. \(\sqrt{48} = \sqrt{16 \times 3}\).
- Step 3: Simplify each square root. \(\sqrt{16} = 4\) and \(\sqrt{3}\) remains as is.
- Step 4: Combine the results. \(\sqrt{48} = 4\sqrt{3}\).
- Example 3: Simplify \(\sqrt{200}\).
- Step 1: Identify the factors. \(200 = 100 \times 2\).
- Step 2: Apply the product rule. \(\sqrt{200} = \sqrt{100 \times 2}\).
- Step 3: Simplify each square root. \(\sqrt{100} = 10\) and \(\sqrt{2}\) remains as is.
- Step 4: Combine the results. \(\sqrt{200} = 10\sqrt{2}\).
By following these steps, you can simplify any radical expression using the product rule of square roots.
Quotient Rule of Square Roots
The quotient rule of square roots allows us to simplify the square root of a fraction by separating the square root of the numerator and the square root of the denominator. This property is particularly useful when working with variables and complex fractions.
The quotient rule can be stated as follows:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}, \quad b \ne 0\]
Let's go through the steps to simplify an expression using the quotient rule:
- Simplify the fraction inside the radical, if possible.
- Apply the quotient rule to rewrite the radical as the quotient of two radicals.
- Simplify the radicals in both the numerator and the denominator.
Here are some examples to illustrate the process:
- Example 1: Simplify \(\sqrt{\frac{27m^3}{196}}\)
- The fraction inside the radical cannot be simplified: \(\frac{27m^3}{196}\).
- Apply the quotient rule: \(\sqrt{\frac{27m^3}{196}} = \frac{\sqrt{27m^3}}{\sqrt{196}}\).
- Simplify the radicals: \(\sqrt{27m^3} = \sqrt{9m^2 \cdot 3m} = 3m\sqrt{3m}\) and \(\sqrt{196} = 14\).
- Thus, \(\sqrt{\frac{27m^3}{196}} = \frac{3m\sqrt{3m}}{14}\).
- Example 2: Simplify \(\sqrt{\frac{45x^5}{y^4}}\)
- The fraction inside the radical cannot be simplified: \(\frac{45x^5}{y^4}\).
- Apply the quotient rule: \(\sqrt{\frac{45x^5}{y^4}} = \frac{\sqrt{45x^5}}{\sqrt{y^4}}\).
- Simplify the radicals: \(\sqrt{45x^5} = \sqrt{9x^4 \cdot 5x} = 3x^2\sqrt{5x}\) and \(\sqrt{y^4} = y^2\).
- Thus, \(\sqrt{\frac{45x^5}{y^4}} = \frac{3x^2\sqrt{5x}}{y^2}\).

Simplifying Radicals with Variables
When dealing with radical expressions that include variables, the goal is to simplify them to their most basic form. Here's a step-by-step guide:
- Identify the Index and Radicand: Determine the index (root) and the radicand (expression under the root).
- Factor the Radicand: Factor the expression under the radical completely.
- Apply the Product Rule: For radicals involving multiplication, simplify by separating each radical.
- Apply the Quotient Rule: For radicals involving division, simplify by separating the radicals.
- Combine Like Terms: If there are multiple radicals with the same index and radicand, combine them under a single radical.
- Simplify Each Radical: Simplify each individual radical expression using the rules of radicals and algebraic techniques.
- Consider Absolute Values: Ensure to use absolute values when necessary, especially with even roots to avoid negative results.
- Examples and Practice: Practice simplifying radicals with variables through examples to reinforce understanding.
Even and Odd Exponents
Understanding the behavior of radicals with even and odd exponents is crucial in simplifying expressions involving variables. Here’s a breakdown:
- Even Exponents: Radicals with even exponents, such as square roots (exponent 2), require absolute values to ensure non-negative results. For example, \( \sqrt{x^2} = |x| \).
- Odd Exponents: Radicals with odd exponents, like cube roots (exponent 3), do not require absolute values since the result can be positive or negative depending on the variable’s sign. For instance, \( \sqrt[3]{x^3} = x \).
- Applying Rules: Apply these rules systematically when simplifying radical expressions with variables to maintain accuracy and clarity.
Simplifying Expressions with Multiple Variables
When simplifying radical expressions involving multiple variables, follow these steps:
- Factorize Each Variable: Factor each variable expression under the radical completely.
- Combine Like Terms: Combine similar terms from different variables under a single radical.
- Apply Radical Rules: Use the rules of radicals to simplify each combined expression.
- Absolute Values: Consider absolute values, especially with even roots, to avoid negative results.
- Check for Simplification: Ensure the expression is simplified as much as possible without radicals.
- Examples and Practice: Practice simplifying expressions with multiple variables to strengthen understanding.
Using Absolute Values in Radical Simplification
Absolute values play a crucial role in simplifying radical expressions, especially when dealing with even roots. Here’s how to utilize them effectively:
- Even Roots: For even roots, such as square roots (\( \sqrt{x^2} \)), use absolute values to ensure non-negative results: \( \sqrt{x^2} = |x| \).
- Odd Roots: Odd roots, like cube roots (\( \sqrt[3]{x^3} \)), do not require absolute values since they can yield both positive and negative results: \( \sqrt[3]{x^3} = x \).
- Complex Expressions: In complex expressions involving variables, apply absolute values to each variable within the radical to avoid incorrect simplifications.
- Verification: Always verify the result by substituting back into the original expression to ensure consistency and correctness.

Examples of Simplifying Radical Expressions
Here are some examples demonstrating how to simplify radical expressions involving variables:
- Simplify \( \sqrt{18x^2} \):
- Factor 18 into \( 9 \times 2 \): \( \sqrt{9 \times 2 \times x^2} \).
- Take the square root of 9: \( 3x \sqrt{2} \).
- Simplify \( \sqrt{25x^4} \):
- Factor 25 into \( 5^2 \): \( \sqrt{5^2 \times x^4} \).
- Take the square root of \( 5^2 \) and \( x^4 \): \( 5x^2 \).
- Simplify \( \sqrt{\frac{9x^2}{4}} \):
- Factor \( \frac{9x^2}{4} \) into \( \frac{9}{4} \times x^2 \): \( \frac{3x}{2} \).
- Take the square root of \( \frac{9}{4} \) and \( x^2 \): \( \frac{3x}{2} \).
Advanced Techniques and Tips
When simplifying radical expressions with variables, advanced techniques can help streamline the process and ensure accuracy. Here are some advanced methods and tips to consider:
Using Prime Factorization
Prime factorization can be a powerful tool for simplifying radicals, especially when dealing with variables. Follow these steps:
- Factor the number and variables inside the radical into their prime factors.
- Group the factors in pairs of identical factors.
- Bring each pair out of the radical as a single factor.
For example:
\(\sqrt{100x^4y^6z^3} = \sqrt{(2 \times 2 \times 5 \times 5 \times x \times x \times x \times x \times y \times y \times y \times y \times y \times y \times z \times z \times z)} = 10x^2y^3|z|\sqrt{z}\)
Handling Even and Odd Exponents
When simplifying variables with exponents inside radicals, the approach differs based on whether the exponents are even or odd:
- If the exponent is even, divide it by 2 and move the variable outside the radical.
- If the exponent is odd, subtract 1 to make it even, then apply the above rule and leave one instance of the variable inside the radical.
Examples:
\(\sqrt{x^{10}} = x^5\)
\(\sqrt{y^9} = y^4\sqrt{y}\)
Simplifying Expressions with Multiple Variables
When dealing with multiple variables, apply the same rules to each variable separately:
\(\sqrt{x^6 y^3} = x^3 \sqrt{y^3} = x^3 y \sqrt{y}\)
Using Absolute Values
Since the square root of a variable squared should always be non-negative, use absolute value symbols where necessary:
\(\sqrt{y^6} = |y^3|\)
Rationalizing the Denominator
To simplify a radical expression with a radical in the denominator, multiply the numerator and denominator by the conjugate of the denominator:
\(\frac{\sqrt{2} + \sqrt{3}}{\sqrt{5} - \sqrt{2}} \times \frac{\sqrt{5} + \sqrt{2}}{\sqrt{5} + \sqrt{2}} = \frac{\sqrt{10} + \sqrt{15} + 2 + \sqrt{6}}{3}\)
General Tips
- Always simplify the radicals as much as possible before performing operations like addition or multiplication.
- Check for common factors and perfect squares to simplify the process.
- Practice with various expressions to become proficient in identifying simplification opportunities.
By mastering these advanced techniques, you can efficiently simplify even the most complex radical expressions involving variables.
Common Mistakes to Avoid
When simplifying radical expressions with variables, there are several common mistakes that students often make. Being aware of these mistakes can help you avoid them and simplify radicals correctly. Here are some of the most frequent errors:
- Incorrectly Combining Radicals: One of the most common mistakes is assuming that the sum or difference of two radicals can be simplified as a single radical. For example, \( \sqrt{a} + \sqrt{b} \neq \sqrt{a + b} \). Always remember that radicals can only be combined if they have the same radicand.
- Ignoring Absolute Values: When simplifying expressions with even exponents, it is essential to use absolute values. For example, \( \sqrt{x^2} = |x| \). This ensures that the result is non-negative, as the square root of a squared term should be positive.
- Incorrect Factorization: Failing to properly factor the radicand can lead to incorrect simplification. Always factor the expression under the radical into its prime factors. For instance, \( \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \).
- Misapplying the Product and Quotient Rules: The product rule (\( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)) and the quotient rule (\( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)) are only valid when \( a \) and \( b \) are non-negative. Applying these rules incorrectly can lead to errors in simplification.
- Overlooking Simplification of Coefficients: Ensure that both the numerical and variable parts of the expression are fully simplified. For example, in \( \sqrt{18x^4} \), simplify both the number and the variable: \( \sqrt{18} = 3\sqrt{2} \) and \( \sqrt{x^4} = x^2 \), so \( \sqrt{18x^4} = 3x^2\sqrt{2} \).
- Incorrect Handling of Variables with Odd Exponents: When dealing with variables that have odd exponents, it is crucial to separate the exponent into an even part and a remainder. For example, \( \sqrt{x^5} = \sqrt{x^4 \times x} = x^2\sqrt{x} \).
- Forgetting to Simplify Radicals Completely: Sometimes, students stop simplifying too early. Ensure that the expression is fully simplified, which may involve factoring out all perfect squares. For instance, \( \sqrt{72} \) should be simplified to \( 6\sqrt{2} \), not just \( \sqrt{72} \).
By keeping these common mistakes in mind and applying the correct rules and methods, you can accurately simplify radical expressions with variables.
Practice Problems and Solutions
Below are some practice problems with detailed solutions to help you understand how to simplify radical expressions with variables.
-
Simplify: \( \sqrt{50x^4y^6} \)
Solution:
- Step 1: Factor the expression inside the radical. \[ \sqrt{50x^4y^6} = \sqrt{2 \cdot 5^2 \cdot x^4 \cdot y^6} \]
- Step 2: Apply the square root to each factor. \[ \sqrt{2 \cdot 5^2 \cdot x^4 \cdot y^6} = \sqrt{2} \cdot \sqrt{5^2} \cdot \sqrt{x^4} \cdot \sqrt{y^6} \]
- Step 3: Simplify each square root. \[ = \sqrt{2} \cdot 5 \cdot x^2 \cdot y^3 \]
- Final Answer: \[ = 5x^2y^3 \sqrt{2} \]
-
Simplify: \( \sqrt[3]{54a^6b^3} \)
Solution:
- Step 1: Factor the expression inside the radical. \[ \sqrt[3]{54a^6b^3} = \sqrt[3]{2 \cdot 3^3 \cdot a^6 \cdot b^3} \]
- Step 2: Apply the cube root to each factor. \[ \sqrt[3]{2 \cdot 3^3 \cdot a^6 \cdot b^3} = \sqrt[3]{2} \cdot \sqrt[3]{3^3} \cdot \sqrt[3]{a^6} \cdot \sqrt[3]{b^3} \]
- Step 3: Simplify each cube root. \[ = \sqrt[3]{2} \cdot 3 \cdot a^2 \cdot b \]
- Final Answer: \[ = 3a^2b \sqrt[3]{2} \]
-
Simplify: \( \frac{6x^3}{\sqrt{8x}} \)
Solution:
- Step 1: Simplify the denominator. \[ \sqrt{8x} = \sqrt{4 \cdot 2x} = 2\sqrt{2x} \]
- Step 2: Rewrite the expression. \[ \frac{6x^3}{2\sqrt{2x}} = \frac{6x^3}{2\sqrt{2x}} = \frac{3x^3}{\sqrt{2x}} \]
- Step 3: Multiply the numerator and the denominator by \( \sqrt{2x} \) to rationalize the denominator. \[ \frac{3x^3 \cdot \sqrt{2x}}{\sqrt{2x} \cdot \sqrt{2x}} = \frac{3x^3 \sqrt{2x}}{2x} = \frac{3x^2 \sqrt{2x}}{2} \]
- Final Answer: \[ = \frac{3x^2 \sqrt{2x}}{2} \]
Practice these problems to master simplifying radical expressions with variables. Understanding each step thoroughly will help you tackle more complex expressions with confidence.

Conclusion
Simplifying radical expressions with variables is an essential skill in algebra, helping to make complex expressions more manageable and easier to work with. By understanding the basic rules and methods, such as prime factorization, the product and quotient rules, and how to handle even and odd exponents, you can effectively simplify these expressions.
Remember to always check for perfect squares and use absolute values where necessary to ensure your simplified expression is accurate and follows mathematical conventions. Working with radicals often requires careful attention to detail, especially when variables are involved, but with practice, these steps become more intuitive.
We encourage you to continue practicing with various problems, including those with multiple variables and higher-order roots, to solidify your understanding and improve your skills. Simplifying radical expressions is not just a theoretical exercise but a practical tool that you will find useful in solving real-world problems in science, engineering, and beyond.
Keep exploring advanced techniques and stay curious about the ways these mathematical concepts apply to different fields. With a strong foundation in simplifying radicals, you will be well-prepared to tackle more advanced topics and challenges in your mathematical journey.
Thank you for following along in this comprehensive guide. We hope it has been informative and helpful in enhancing your understanding of simplifying radical expressions with variables.
Hướng dẫn đơn giản hóa biểu thức căn với biến số, số mũ, phân số, căn bậc ba trong đại số. Phù hợp cho người học muốn nắm vững kiến thức cơ bản và nâng cao.
Đơn Giản Hóa Biểu Thức Căn Với Biến Số, Số Mũ, Phân Số, Căn Bậc Ba - Đại Số
READ MORE:
Hướng dẫn đơn giản hóa biểu thức căn với biến, giúp bạn hiểu rõ và áp dụng các bước một cách dễ dàng.
Đơn Giản Hóa Biểu Thức Căn Với Biến