Topic right triangle perimeter formula: Discover the simplicity of calculating the perimeter of a right triangle with our comprehensive guide. Whether you're a student, teacher, or math enthusiast, our step-by-step instructions and practical examples will make mastering the right triangle perimeter formula easy and enjoyable. Join us to enhance your geometry skills today!
Table of Content
- Right Triangle Perimeter Formula
- Introduction to Right Triangle Perimeter
- Basic Concepts of Right Triangles
- Understanding Perimeter in Geometry
- Formula for the Perimeter of a Right Triangle
- Derivation of the Perimeter Formula
- Examples and Applications
- Solving Perimeter Problems
- Common Mistakes to Avoid
- Advanced Topics Related to Right Triangle Perimeters
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Học cách tính diện tích và chu vi của tam giác vuông với Thầy J trong video này. Thích hợp cho học sinh muốn nắm vững kiến thức cơ bản về hình học.
Right Triangle Perimeter Formula
A right triangle is a type of triangle that has one angle equal to 90 degrees. The perimeter of a right triangle is the sum of the lengths of its three sides: the base, the height, and the hypotenuse. The formula for calculating the perimeter is:
\[ \text{Perimeter} = a + b + c \]
where:
- \( a \) is the length of the base
- \( b \) is the length of the height
- \( c \) is the length of the hypotenuse
Examples
-
Example 1: Find the perimeter of a right-angled triangle if its base is 4 units, height is 3 units, and the hypotenuse is 5 units.
\[ \text{Perimeter} = 4 + 3 + 5 = 12 \text{ units} \] -
Example 2: In a right-angled triangle, if the base is 6 units and the height is 8 units, find its perimeter.
First, find the hypotenuse using the Pythagorean theorem:
\[ c = \sqrt{a^2 + b^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ units} \]Now, calculate the perimeter:
\[ \text{Perimeter} = 6 + 8 + 10 = 24 \text{ units} \] -
Example 3: Find the perimeter of a right triangle if the base is 5 units and the hypotenuse is 13 units.
First, find the height using the Pythagorean theorem:
\[ b = \sqrt{c^2 - a^2} = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12 \text{ units} \]
\[ \text{Perimeter} = 5 + 12 + 13 = 30 \text{ units} \]
Additional Information
The perimeter of a right-angled triangle can be used in various real-life applications, including construction and navigation. Understanding the properties and formulas related to right triangles is fundamental in the study of geometry and trigonometry.
Useful Formulas
- Pythagorean Theorem: \( c^2 = a^2 + b^2 \)
- Area of a Right Triangle: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
| Base (a) | Height (b) | Hypotenuse (c) | Perimeter |
| 4 | 3 | 5 | 12 |
| 6 | 8 | 10 | 24 |
| 5 | 12 | 13 | 30 |

READ MORE:
Introduction to Right Triangle Perimeter
A right triangle is a type of triangle that has one angle measuring 90 degrees. The sides of a right triangle are typically referred to as the two legs and the hypotenuse, where the hypotenuse is the longest side opposite the right angle.
The perimeter of a right triangle is the sum of the lengths of its three sides. To calculate the perimeter, you need to know the lengths of all three sides. The formula for the perimeter \(P\) is:
\[
P = a + b + c
\]
where \(a\) and \(b\) are the lengths of the legs, and \(c\) is the length of the hypotenuse.
Here's a step-by-step guide to understanding the right triangle perimeter:
- Identify the sides: Determine which sides are the legs (\(a\) and \(b\)) and which side is the hypotenuse (\(c\)).
- Measure the sides: Measure the lengths of the legs and the hypotenuse. If the hypotenuse is not known, it can be calculated using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} \]
- Apply the perimeter formula: Add the lengths of the three sides using the perimeter formula: \[ P = a + b + c \]
Let's look at an example. Suppose a right triangle has legs of lengths 3 units and 4 units. First, calculate the hypotenuse:
\[
c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5
\]
Now, add the lengths of all three sides to find the perimeter:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
This process demonstrates the simplicity and effectiveness of calculating the perimeter of a right triangle using the basic geometric principles and the Pythagorean theorem.
Basic Concepts of Right Triangles
Understanding the basic concepts of right triangles is essential for solving various geometric problems. A right triangle is a triangle in which one of the angles is exactly 90 degrees. The side opposite this right angle is the hypotenuse, the longest side, while the other two sides are called the legs.
Here are the key concepts of right triangles:
- Right Angle: A right triangle has one angle that is exactly 90 degrees. This right angle is denoted by a small square in the triangle's corner.
- Legs of the Triangle: The two sides that form the right angle are called the legs. These sides are perpendicular to each other.
- Hypotenuse: The hypotenuse is the side opposite the right angle and is the longest side of the right triangle. It can be calculated using the Pythagorean theorem if the lengths of the legs are known: \[ c = \sqrt{a^2 + b^2} \] where \(c\) is the hypotenuse, and \(a\) and \(b\) are the lengths of the legs.
- Pythagorean Theorem: This fundamental theorem states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs: \[ a^2 + b^2 = c^2 \]
- Special Right Triangles: Some right triangles have side lengths that follow specific ratios, such as the 45-45-90 triangle and the 30-60-90 triangle. These triangles have unique properties that simplify calculations.
Let's consider an example to illustrate these concepts. Suppose we have a right triangle with legs of lengths 6 units and 8 units. To find the hypotenuse, we use the Pythagorean theorem:
\[
c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10
\]
Thus, the hypotenuse is 10 units long. By understanding these basic concepts, you can easily work with right triangles and solve a variety of geometric problems.
Understanding Perimeter in Geometry
The perimeter is a fundamental concept in geometry that refers to the total distance around the boundary of a two-dimensional shape. It is an important measure in various geometric applications, such as construction, land surveying, and everyday calculations.
In geometry, the perimeter can be calculated for different shapes using specific formulas. Here is a step-by-step guide to understanding and calculating the perimeter for some common shapes:
-
Perimeter of a Square:
- All four sides of a square are equal in length.
- The formula for the perimeter \(P\) of a square with side length \(s\) is: \[ P = 4s \]
-
Perimeter of a Rectangle:
- A rectangle has opposite sides that are equal in length.
- The formula for the perimeter \(P\) of a rectangle with length \(l\) and width \(w\) is: \[ P = 2l + 2w \]
-
Perimeter of a Triangle:
- A triangle has three sides, and the perimeter is the sum of the lengths of all three sides.
- The formula for the perimeter \(P\) of a triangle with side lengths \(a\), \(b\), and \(c\) is: \[ P = a + b + c \]
-
Perimeter of a Right Triangle:
- In a right triangle, one angle is 90 degrees.
- The two shorter sides are the legs, and the longest side is the hypotenuse.
- If the lengths of the legs are \(a\) and \(b\), and the hypotenuse is \(c\), the perimeter \(P\) is: \[ P = a + b + c \]
Let's look at an example of calculating the perimeter of a right triangle. Suppose a right triangle has legs of lengths 5 units and 12 units. First, calculate the hypotenuse using the Pythagorean theorem:
\[
c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13
\]
Now, sum the lengths of all three sides to find the perimeter:
\[
P = 5 + 12 + 13 = 30 \text{ units}
\]
Understanding the perimeter in geometry allows for accurate measurement and calculation in various practical and theoretical contexts. Mastering these fundamental concepts enables more complex problem-solving and application in diverse fields.
Formula for the Perimeter of a Right Triangle
The perimeter of a right triangle is the total distance around the triangle. It is the sum of the lengths of its three sides: the two legs and the hypotenuse. The formula for calculating the perimeter of a right triangle is straightforward and relies on knowing the lengths of these sides.
Here is the step-by-step process for finding the perimeter of a right triangle:
-
Identify the Sides:
- The right triangle has three sides: the two legs (\(a\) and \(b\)) and the hypotenuse (\(c\)).
-
Measure the Legs:
- Determine the lengths of the two legs. These are the sides that form the right angle.
-
Calculate the Hypotenuse (if not given):
- If the hypotenuse is not known, use the Pythagorean theorem to find it: \[ c = \sqrt{a^2 + b^2} \]
-
Apply the Perimeter Formula:
- Once you have the lengths of all three sides, sum them to find the perimeter: \[ P = a + b + c \]
Let's look at a practical example:
Suppose you have a right triangle with legs of lengths 7 units and 24 units. First, calculate the hypotenuse:
\[
c = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25
\]
Now, use the perimeter formula:
\[
P = 7 + 24 + 25 = 56 \text{ units}
\]
Therefore, the perimeter of the right triangle is 56 units. This simple process allows you to quickly and accurately determine the perimeter of any right triangle as long as you know the lengths of its sides.
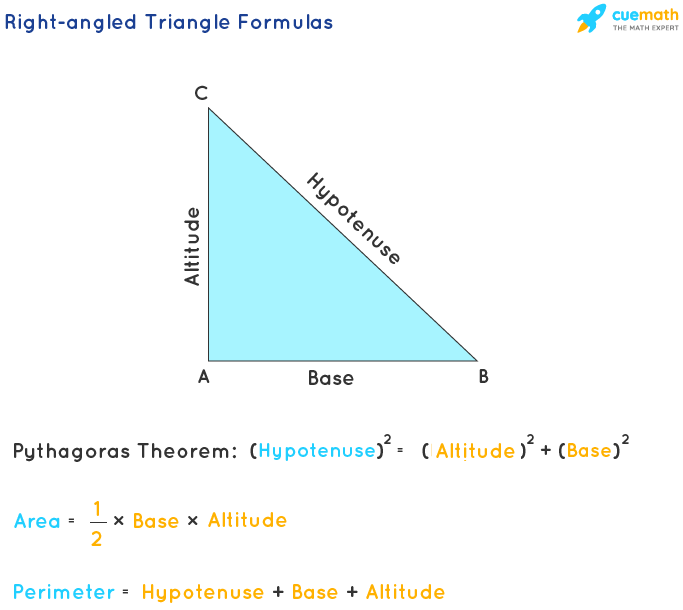
Derivation of the Perimeter Formula
Deriving the perimeter formula for a right triangle involves understanding the relationship between its sides. A right triangle consists of two legs and a hypotenuse. The legs form the right angle, and the hypotenuse is the side opposite the right angle.
The perimeter \(P\) of a right triangle is the sum of the lengths of its three sides: the two legs (\(a\) and \(b\)) and the hypotenuse (\(c\)). The formula is given by:
\[
P = a + b + c
\]
Here is a step-by-step derivation of this formula:
-
Identify the Sides of the Triangle:
- The two legs of the right triangle are \(a\) and \(b\).
- The hypotenuse is \(c\).
-
Use the Pythagorean Theorem:
- The Pythagorean theorem states that the square of the hypotenuse is equal to the sum of the squares of the legs: \[ c^2 = a^2 + b^2 \]
-
Solve for the Hypotenuse:
- To find the hypotenuse \(c\), take the square root of both sides of the equation: \[ c = \sqrt{a^2 + b^2} \]
-
Substitute the Hypotenuse into the Perimeter Formula:
- Now that we have the expression for \(c\), we can substitute it into the perimeter formula: \[ P = a + b + \sqrt{a^2 + b^2} \]
Let's look at an example to illustrate this derivation. Suppose we have a right triangle with legs of lengths 9 units and 12 units. First, we calculate the hypotenuse:
\[
c = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15
\]
Next, we use the perimeter formula:
\[
P = 9 + 12 + 15 = 36 \text{ units}
\]
This derivation shows how the perimeter of a right triangle can be calculated by understanding the geometric relationships between its sides and applying the Pythagorean theorem. By following these steps, you can accurately determine the perimeter of any right triangle.
Examples and Applications
Understanding the perimeter of a right triangle is crucial in various real-world scenarios and mathematical problems. Here, we will explore some examples and applications to illustrate how to use the perimeter formula in different contexts.
Example 1: Basic Calculation
Suppose you have a right triangle with legs of lengths 6 units and 8 units. To find the perimeter:
- Calculate the hypotenuse using the Pythagorean theorem: \[ c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \]
- Sum the lengths of the three sides: \[ P = 6 + 8 + 10 = 24 \text{ units} \]
Example 2: Application in Construction
Imagine you are designing a triangular ramp for accessibility. The ramp must have a base of 12 feet and a height of 5 feet. To find the amount of edging needed (perimeter):
- Calculate the hypotenuse: \[ c = \sqrt{12^2 + 5^2} = \sqrt{144 + 25} = \sqrt{169} = 13 \]
- Determine the perimeter: \[ P = 12 + 5 + 13 = 30 \text{ feet} \]
Example 3: Triangular Garden Bed
You want to create a triangular garden bed with sides of lengths 7 feet, 24 feet, and the hypotenuse. To calculate the amount of fencing needed (perimeter):
- Calculate the hypotenuse: \[ c = \sqrt{7^2 + 24^2} = \sqrt{49 + 576} = \sqrt{625} = 25 \]
- Find the perimeter: \[ P = 7 + 24 + 25 = 56 \text{ feet} \]
Application in Navigation
In navigation, right triangles are often used to calculate shortest paths. For example, if a ship sails 3 miles east and then 4 miles north, the direct path (hypotenuse) can be calculated, and the perimeter gives the total distance traveled:
- Calculate the hypotenuse: \[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Calculate the total distance traveled: \[ P = 3 + 4 + 5 = 12 \text{ miles} \]
These examples demonstrate the versatility and practicality of the perimeter formula for right triangles in various fields such as construction, gardening, and navigation. By mastering this formula, you can tackle numerous real-world problems efficiently.
Solving Perimeter Problems
Solving perimeter problems involving right triangles requires a systematic approach. Here, we will outline a step-by-step method to solve these problems effectively, along with practical examples.
Step-by-Step Approach
-
Identify the Given Information:
- Determine which sides of the right triangle are given (legs or hypotenuse).
-
Use the Pythagorean Theorem (if necessary):
- If the hypotenuse is not provided, calculate it using the Pythagorean theorem: \[ c = \sqrt{a^2 + b^2} \]
-
Apply the Perimeter Formula:
- Sum the lengths of all three sides: \[ P = a + b + c \]
-
Verify Your Solution:
- Check your calculations to ensure accuracy.
Example 1: Finding the Perimeter
Suppose you have a right triangle with legs of lengths 9 units and 12 units. To find the perimeter:
- Calculate the hypotenuse: \[ c = \sqrt{9^2 + 12^2} = \sqrt{81 + 144} = \sqrt{225} = 15 \]
- Apply the perimeter formula: \[ P = 9 + 12 + 15 = 36 \text{ units} \]
Example 2: Perimeter with a Given Hypotenuse
If a right triangle has one leg of 5 units and a hypotenuse of 13 units, find the perimeter:
- Use the Pythagorean theorem to find the other leg: \[ b = \sqrt{c^2 - a^2} = \sqrt{13^2 - 5^2} = \sqrt{169 - 25} = \sqrt{144} = 12 \]
- Apply the perimeter formula: \[ P = 5 + 12 + 13 = 30 \text{ units} \]
Example 3: Real-World Application
Consider a triangular plot of land where one leg is 20 meters, and the other leg is 21 meters. To find the total length of fencing needed (perimeter):
- Calculate the hypotenuse: \[ c = \sqrt{20^2 + 21^2} = \sqrt{400 + 441} = \sqrt{841} = 29 \]
- Find the perimeter: \[ P = 20 + 21 + 29 = 70 \text{ meters} \]
By following these steps, you can accurately solve perimeter problems for right triangles. Understanding and applying the perimeter formula enables you to address various practical and theoretical challenges efficiently.
Common Mistakes to Avoid
When calculating the perimeter of a right triangle, several common mistakes can occur. Being aware of these pitfalls can help ensure accuracy in your calculations:
- Incorrect Identification of the Hypotenuse: Always remember that the hypotenuse is the longest side of the right triangle, opposite the right angle. Misidentifying the sides can lead to incorrect calculations.
- Misapplication of the Pythagorean Theorem: Ensure that you correctly apply the Pythagorean theorem, \( a^2 + b^2 = c^2 \), where \(c\) is the hypotenuse. Misplacing the sides in the equation can result in errors.
- Forgetting to Sum All Three Sides: The perimeter of a right triangle is the sum of all three sides, \(a + b + c\). Sometimes, only two sides are considered, leading to an incomplete perimeter calculation.
- Incorrect Units: Ensure all sides are measured in the same units before calculating the perimeter. Mixing units can result in incorrect calculations.
- Calculation Errors: Simple arithmetic errors can occur when summing the sides. Double-check your calculations to ensure accuracy.
- Rounding Errors: Be careful with rounding intermediate values. It's best to round only the final answer to maintain precision.
By being mindful of these common mistakes, you can improve your accuracy when calculating the perimeter of a right triangle.
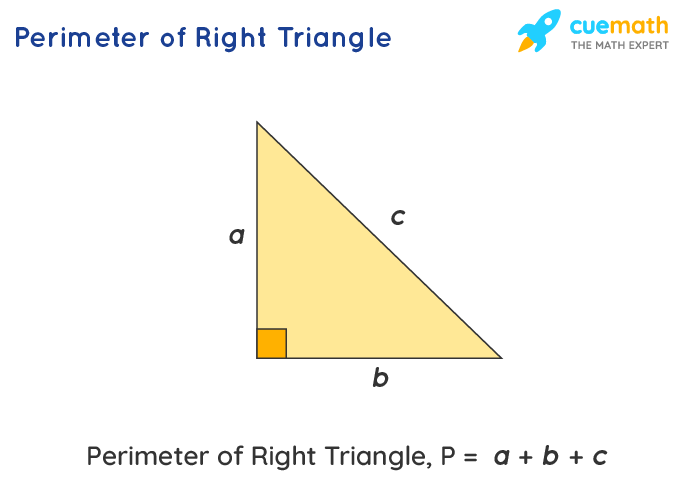
Advanced Topics Related to Right Triangle Perimeters
Right triangles are a fundamental part of geometry, and their perimeters offer interesting insights and advanced applications. Here, we will explore several advanced topics related to the perimeters of right triangles, including special right triangles, the relationship with trigonometry, and applications in real-world problems.
Special Right Triangles
Two commonly studied special right triangles are the 45-45-90 triangle and the 30-60-90 triangle. These triangles have unique properties that simplify calculations.
- 45-45-90 Triangle: This is an isosceles right triangle where the two legs are of equal length. The hypotenuse is \( \sqrt{2} \) times the length of each leg. The perimeter formula for a 45-45-90 triangle, with leg length \( a \), is: \[ P = a + a + a\sqrt{2} = 2a + a\sqrt{2} \]
- 30-60-90 Triangle: In this triangle, the sides are in the ratio 1 : \( \sqrt{3} \) : 2. The perimeter of a 30-60-90 triangle, with the shortest side \( a \), is: \[ P = a + a\sqrt{3} + 2a = a(1 + \sqrt{3} + 2) \]
Trigonometric Relationships
Trigonometric functions are essential for solving problems involving right triangles. The sine, cosine, and tangent functions relate the angles of a right triangle to its side lengths. These relationships can help determine unknown side lengths and, consequently, the perimeter.
- Sine Function: \( \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \)
- Cosine Function: \( \cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}} \)
- Tangent Function: \( \tan(\theta) = \frac{\text{opposite}}{\text{adjacent}} \)
Applications in Real-World Problems
Right triangle perimeter calculations are crucial in various real-world scenarios, such as construction, navigation, and physics. For example, engineers often use right triangles to determine distances and angles when designing structures. In navigation, right triangles help calculate shortest paths and angles of elevation.
- Construction: Ensuring the stability and proper alignment of structures by calculating accurate measurements.
- Navigation: Determining the shortest route between two points and the necessary course corrections.
- Physics: Analyzing components of forces and velocities that form right-angled triangles.
Decomposition of Shapes
Complex shapes can often be decomposed into right triangles, making it easier to calculate perimeters and areas. For instance, a parallelogram can be divided into two right triangles and a rectangle, allowing for simpler calculations using known formulas.
Understanding these advanced topics provides a deeper insight into the practical applications and significance of right triangle perimeters in both theoretical and applied contexts.
Frequently Asked Questions
Here are some common questions and detailed answers related to the perimeter of a right triangle:
-
What is the formula for the perimeter of a right triangle?
The perimeter of a right triangle is calculated by adding the lengths of its three sides. If the lengths of the legs are \(a\) and \(b\), and the hypotenuse is \(c\), the formula is:
\[
P = a + b + c
\] -
How do I find the hypotenuse if only the legs are known?
Use the Pythagorean theorem to find the hypotenuse. If \(a\) and \(b\) are the legs of the right triangle, the hypotenuse \(c\) can be found using:
\[
c = \sqrt{a^2 + b^2}
\] -
Can the perimeter of a right triangle be calculated if only two sides are known?
Yes, you can calculate the perimeter if you know two sides. If you know one leg and the hypotenuse, you can find the other leg using the Pythagorean theorem, and then sum all three sides to find the perimeter.
-
What units should be used for the perimeter calculation?
The units for the perimeter should be consistent with the units of the sides of the triangle. If the sides are in meters, the perimeter will be in meters; if in centimeters, the perimeter will be in centimeters, and so on.
-
How does the Pythagorean theorem relate to the perimeter of a right triangle?
The Pythagorean theorem helps in calculating the hypotenuse if the lengths of the other two sides are known. This is crucial for determining the perimeter when only the legs are initially known.
-
Are there any common mistakes to avoid when calculating the perimeter?
Yes, some common mistakes include:
- Forgetting to use the Pythagorean theorem to find the hypotenuse.
- Mixing units of measurement without proper conversion.
- Incorrectly adding the sides due to calculation errors.
- Rounding numbers too early in the calculation process, leading to inaccuracies.
Conclusion
Understanding the perimeter of a right triangle is fundamental in both basic and advanced geometry. The perimeter, which is the sum of all the sides of the triangle, can be calculated using the formula:
\[ \text{Perimeter} = a + b + c \]
where \(a\) and \(b\) are the legs and \(c\) is the hypotenuse of the right triangle. This formula is straightforward yet crucial for solving various geometric problems.
Throughout this guide, we have explored the derivation of the perimeter formula, solved practical examples, and discussed common mistakes to avoid. We also delved into advanced topics such as the relationship between the perimeter and other geometric properties, including the area and the Pythagorean theorem.
Applying these concepts correctly ensures accurate calculations and a deeper understanding of geometric principles. Whether you're a student, educator, or geometry enthusiast, mastering the perimeter formula of a right triangle enhances your mathematical toolkit and problem-solving skills.
In summary, the perimeter of a right triangle encapsulates the essence of geometric measurement and offers a gateway to more complex mathematical explorations. By practicing and applying these principles, you can navigate a wide range of mathematical challenges with confidence and precision.
We hope this comprehensive guide has provided valuable insights and practical knowledge on the right triangle perimeter formula. Continue to explore and practice, and you'll find that geometry becomes a more intuitive and enjoyable subject.
Học cách tính diện tích và chu vi của tam giác vuông với Thầy J trong video này. Thích hợp cho học sinh muốn nắm vững kiến thức cơ bản về hình học.
Diện Tích và Chu Vi của Tam Giác Vuông | Toán với Thầy J
READ MORE:
Hướng dẫn cách tìm diện tích và chu vi của tam giác vuông một cách dễ hiểu và chi tiết.
Cách Tìm Diện Tích và Chu Vi của Tam Giác Vuông