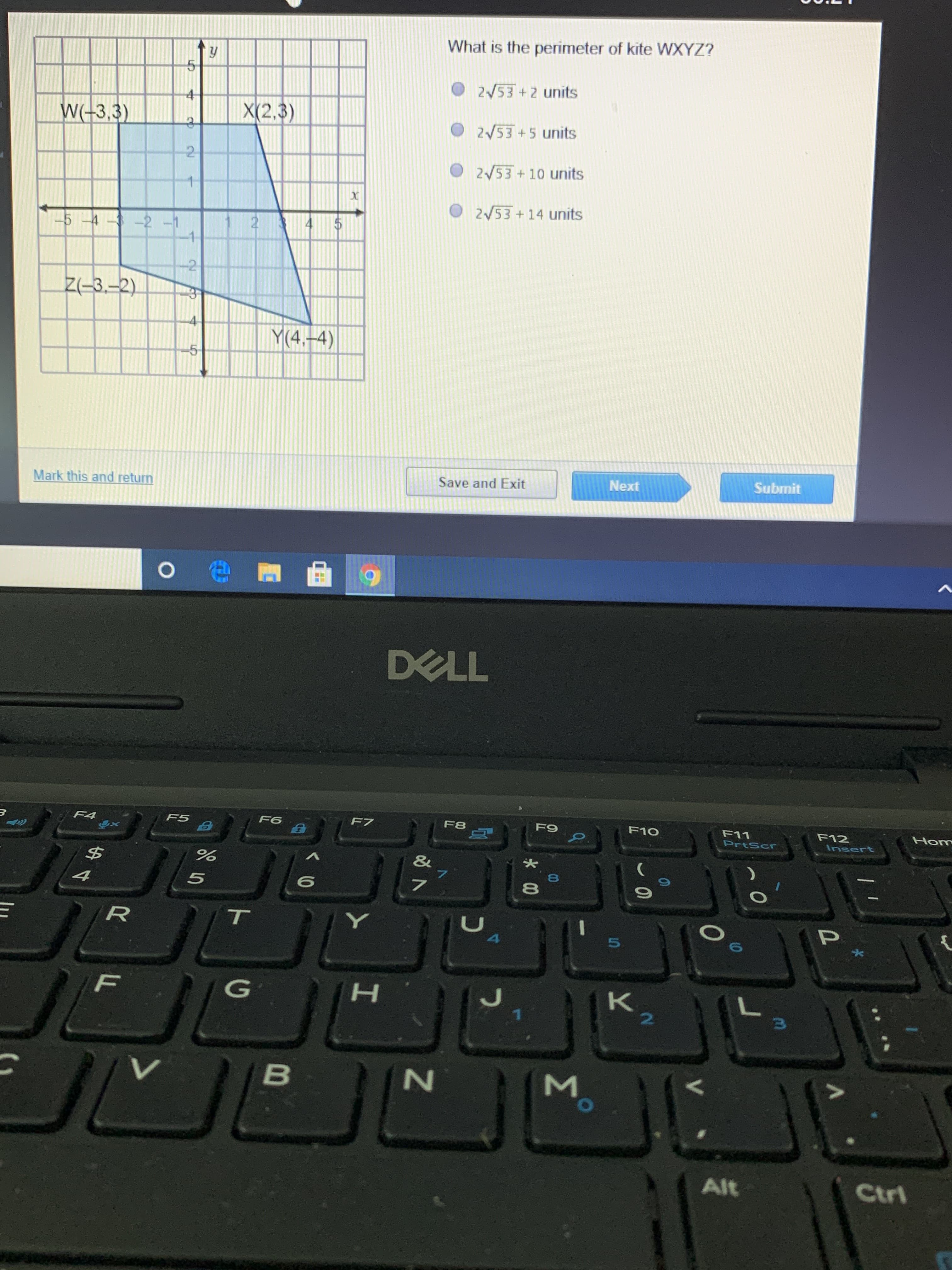
Topic perimeter and area formula of all shapes: Discover the ultimate guide to the perimeter and area formulas of all shapes. This comprehensive article covers everything from basic squares and circles to complex polygons and ellipses, providing clear and concise formulas for each shape. Perfect for students, educators, and anyone looking to master geometry effortlessly.
Table of Content
- Perimeter and Area Formulas of All Shapes
- Introduction to Perimeter and Area
- Basic Shapes and Their Formulas
- Square: Perimeter and Area
- Rectangle: Perimeter and Area
- Triangle: Perimeter and Area
- Circle: Circumference and Area
- Advanced Geometric Shapes
- Parallelogram: Perimeter and Area
- Rhombus: Perimeter and Area
- Trapezoid: Perimeter and Area
- Ellipse: Circumference and Area
- Regular Polygon: Perimeter and Area
- Special Cases and Complex Shapes
- Formulas for Composite Shapes
- Formulas for Irregular Shapes
- Applications of Perimeter and Area Formulas
- Real-world Examples
- Frequently Asked Questions (FAQ)
- YOUTUBE:
Perimeter and Area Formulas of All Shapes
Here are the perimeter and area formulas for various geometric shapes:
1. Square
- Perimeter: \( P = 4a \)
- Area: \( A = a^2 \)
2. Rectangle
- Perimeter: \( P = 2(l + w) \)
- Area: \( A = lw \)
3. Triangle
- Perimeter: \( P = a + b + c \)
- Area: \( A = \frac{1}{2}bh \)
4. Circle
- Circumference: \( C = 2\pi r \)
- Area: \( A = \pi r^2 \)
5. Parallelogram
- Perimeter: \( P = 2(a + b) \)
- Area: \( A = bh \)
6. Rhombus
- Area: \( A = \frac{1}{2}d_1 d_2 \)
7. Trapezoid
- Perimeter: \( P = a + b + c + d \)
- Area: \( A = \frac{1}{2}(a + b)h \)
8. Ellipse
- Circumference: \( C \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}} \)
- Area: \( A = \pi ab \)
9. Regular Polygon (n sides)
- Perimeter: \( P = ns \)
- Area: \( A = \frac{1}{4}ns^2 \cot \left(\frac{\pi}{n}\right) \)
| Shape | Perimeter/Circumference Formula | Area Formula |
|---|---|---|
| Square | \( P = 4a \) | \( A = a^2 \) |
| Rectangle | \( P = 2(l + w) \) | \( A = lw \) |
| Triangle | \( P = a + b + c \) | \( A = \frac{1}{2}bh \) |
| Circle | \( C = 2\pi r \) | \( A = \pi r^2 \) |
| Parallelogram | \( P = 2(a + b) \) | \( A = bh \) |
| Rhombus | \( P = 4a \) | \( A = \frac{1}{2}d_1 d_2 \) |
| Trapezoid | \( P = a + b + c + d \) | \( A = \frac{1}{2}(a + b)h \) |
| Ellipse | \( C \approx 2\pi \sqrt{\frac{a^2 + b^2}{2}} \) | \( A = \pi ab \) |
| Regular Polygon | \( P = ns \) | \( A = \frac{1}{4}ns^2 \cot \left(\frac{\pi}{n}\right) \) |

READ MORE:
Introduction to Perimeter and Area
Understanding the concepts of perimeter and area is fundamental in geometry. These measurements are essential for various applications, from simple construction projects to complex engineering designs. This guide aims to provide a comprehensive overview of perimeter and area formulas for a variety of geometric shapes, both basic and advanced.
Perimeter refers to the total length of the boundary of a two-dimensional shape. It is the distance around the shape and can be calculated by summing the lengths of all sides. The formula varies depending on the shape:
- Square: \( P = 4a \) where \( a \) is the side length.
- Rectangle: \( P = 2(l + w) \) where \( l \) is the length and \( w \) is the width.
- Triangle: \( P = a + b + c \) where \( a \), \( b \), and \( c \) are the lengths of the sides.
- Circle (Circumference): \( C = 2\pi r \) where \( r \) is the radius.
Area measures the amount of space inside a two-dimensional shape. The calculation of area also depends on the type of shape:
- Square: \( A = a^2 \) where \( a \) is the side length.
- Rectangle: \( A = lw \) where \( l \) is the length and \( w \) is the width.
- Triangle: \( A = \frac{1}{2}bh \) where \( b \) is the base and \( h \) is the height.
- Circle: \( A = \pi r^2 \) where \( r \) is the radius.
These basic formulas provide the foundation for understanding more complex shapes and their respective perimeter and area calculations. By mastering these, you will be well-equipped to tackle a variety of geometric problems.
Basic Shapes and Their Formulas
In this section, we will explore the perimeter and area formulas for basic geometric shapes. These formulas are essential tools in geometry and are used in various practical applications. Understanding these fundamental shapes and their properties is crucial for solving more complex geometric problems.
Square
The square is a four-sided shape with all sides of equal length and all angles right angles.
- Perimeter: \( P = 4a \) where \( a \) is the side length.
- Area: \( A = a^2 \)
Rectangle
The rectangle has opposite sides of equal length and all angles are right angles.
- Perimeter: \( P = 2(l + w) \) where \( l \) is the length and \( w \) is the width.
- Area: \( A = lw \)
Triangle
Triangles have three sides and the sum of the internal angles is always 180 degrees. There are different types of triangles, but the basic formulas apply to all.
- Perimeter: \( P = a + b + c \) where \( a \), \( b \), and \( c \) are the lengths of the sides.
- Area: \( A = \frac{1}{2}bh \) where \( b \) is the base and \( h \) is the height.
Circle
The circle is a shape with all points the same distance from the center. This distance is called the radius.
- Circumference (Perimeter): \( C = 2\pi r \) where \( r \) is the radius.
- Area: \( A = \pi r^2 \)
Parallelogram
A parallelogram has opposite sides that are equal and parallel.
- Perimeter: \( P = 2(a + b) \) where \( a \) and \( b \) are the lengths of the sides.
- Area: \( A = bh \) where \( b \) is the base and \( h \) is the height.
Rhombus
A rhombus is a type of parallelogram where all sides are of equal length.
- Perimeter: \( P = 4a \) where \( a \) is the side length.
- Area: \( A = \frac{1}{2}d_1d_2 \) where \( d_1 \) and \( d_2 \) are the lengths of the diagonals.
Trapezoid
A trapezoid has one pair of parallel sides.
- Perimeter: \( P = a + b + c + d \) where \( a \) and \( b \) are the lengths of the parallel sides and \( c \) and \( d \) are the lengths of the non-parallel sides.
- Area: \( A = \frac{1}{2}(a + b)h \) where \( h \) is the height (the perpendicular distance between the parallel sides).
Ellipse
An ellipse is an elongated circle with two axes: a major axis and a minor axis.
- Circumference (Approximation): \( C \approx \pi \left[3(a + b) - \sqrt{(3a + b)(a + 3b)}\right] \) where \( a \) is the semi-major axis and \( b \) is the semi-minor axis.
- Area: \( A = \pi ab \)
Regular Polygon
A regular polygon has all sides and angles equal. The formulas depend on the number of sides \( n \) and the length of each side \( s \).
- Perimeter: \( P = ns \)
- Area: \( A = \frac{1}{4}ns^2 \cot(\pi/n) \)
Square: Perimeter and Area
A square is a simple geometric shape with four equal sides and four right angles. The calculations for its perimeter and area are straightforward, but understanding these fundamentals is essential for more advanced geometry. Below are the detailed steps to find the perimeter and area of a square.
Perimeter of a Square
The perimeter of a square is the total length of all its sides. Since all sides of a square are equal, the perimeter is four times the length of one side.
- Let \( a \) represent the length of one side of the square.
- The formula for the perimeter (\( P \)) of a square is:
\( P = 4a \)
For example, if the side length \( a \) is 5 units, then the perimeter is calculated as:
\( P = 4 \times 5 = 20 \) units
Area of a Square
The area of a square is the amount of space enclosed within its sides. It is calculated by squaring the length of one of its sides.
- Let \( a \) represent the length of one side of the square.
- The formula for the area (\( A \)) of a square is:
\( A = a^2 \)
For example, if the side length \( a \) is 5 units, then the area is calculated as:
\( A = 5^2 = 25 \) square units
Step-by-Step Calculation
To ensure clarity, let's outline the steps to calculate the perimeter and area of a square:
- Determine the length of one side: Measure or identify the length of one side of the square. Let this length be \( a \).
- Calculate the perimeter: Use the formula \( P = 4a \) to find the perimeter.
- Calculate the area: Use the formula \( A = a^2 \) to find the area.
Example Calculation
Let's consider a square with a side length of 7 units:
- Perimeter:
- Area:
\( P = 4 \times 7 = 28 \) units
\( A = 7^2 = 49 \) square units
By mastering these simple formulas, you can easily determine the perimeter and area of any square, which is a foundational skill in geometry.
Rectangle: Perimeter and Area
A rectangle is a quadrilateral with opposite sides that are equal and parallel, and all four angles are right angles. Calculating the perimeter and area of a rectangle is fundamental in geometry and practical applications. Below are the detailed steps to determine the perimeter and area of a rectangle.
Perimeter of a Rectangle
The perimeter of a rectangle is the total distance around the edge of the shape. It can be found by adding together the lengths of all four sides.
- Let \( l \) represent the length of the rectangle.
- Let \( w \) represent the width of the rectangle.
- The formula for the perimeter (\( P \)) of a rectangle is:
\( P = 2l + 2w \)
For example, if the length \( l \) is 8 units and the width \( w \) is 5 units, the perimeter is calculated as:
\( P = 2 \times 8 + 2 \times 5 = 16 + 10 = 26 \) units
Area of a Rectangle
The area of a rectangle is the amount of space enclosed within its sides. It is calculated by multiplying the length by the width.
- Let \( l \) represent the length of the rectangle.
- Let \( w \) represent the width of the rectangle.
- The formula for the area (\( A \)) of a rectangle is:
\( A = lw \)
For example, if the length \( l \) is 8 units and the width \( w \) is 5 units, the area is calculated as:
\( A = 8 \times 5 = 40 \) square units
Step-by-Step Calculation
To ensure clarity, let's outline the steps to calculate the perimeter and area of a rectangle:
- Determine the length and width: Measure or identify the length (\( l \)) and width (\( w \)) of the rectangle.
- Calculate the perimeter: Use the formula \( P = 2l + 2w \) to find the perimeter.
- Calculate the area: Use the formula \( A = lw \) to find the area.
Example Calculation
Let's consider a rectangle with a length of 12 units and a width of 7 units:
- Perimeter:
- Area:
\( P = 2 \times 12 + 2 \times 7 = 24 + 14 = 38 \) units
\( A = 12 \times 7 = 84 \) square units
By mastering these basic formulas, you can easily determine the perimeter and area of any rectangle, which is a vital skill in geometry.

Triangle: Perimeter and Area
A triangle is a polygon with three edges and three vertices. Understanding how to calculate the perimeter and area of a triangle is essential in geometry. There are several types of triangles, such as equilateral, isosceles, and scalene, but the basic principles for calculating perimeter and area apply to all. Below are the detailed steps to determine the perimeter and area of a triangle.
Perimeter of a Triangle
The perimeter of a triangle is the total length of its sides. It is calculated by adding the lengths of all three sides.
- Let \( a \), \( b \), and \( c \) represent the lengths of the sides of the triangle.
- The formula for the perimeter (\( P \)) of a triangle is:
\( P = a + b + c \)
For example, if the sides of a triangle are 3 units, 4 units, and 5 units, the perimeter is calculated as:
\( P = 3 + 4 + 5 = 12 \) units
Area of a Triangle
The area of a triangle is the amount of space enclosed within its sides. The most common formula for calculating the area uses the base and height of the triangle:
- Let \( b \) represent the base of the triangle.
- Let \( h \) represent the height of the triangle (the perpendicular distance from the base to the opposite vertex).
- The formula for the area (\( A \)) of a triangle is:
\( A = \frac{1}{2}bh \)
For example, if the base \( b \) is 6 units and the height \( h \) is 4 units, the area is calculated as:
\( A = \frac{1}{2} \times 6 \times 4 = 12 \) square units
Heron's Formula
For a triangle where the height is not known, Heron's formula can be used to calculate the area. This formula only requires the lengths of the sides.
- Let \( a \), \( b \), and \( c \) represent the lengths of the sides of the triangle.
- First, calculate the semi-perimeter (\( s \)):
\( s = \frac{a + b + c}{2} \)
- Then, the formula for the area (\( A \)) of a triangle is:
\( A = \sqrt{s(s - a)(s - b)(s - c)} \)
For example, if the sides of a triangle are 5 units, 6 units, and 7 units:
\( s = \frac{5 + 6 + 7}{2} = 9 \)
\( A = \sqrt{9(9 - 5)(9 - 6)(9 - 7)} = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} \approx 14.7 \) square units
Step-by-Step Calculation
To ensure clarity, let's outline the steps to calculate the perimeter and area of a triangle:
- Determine the lengths of the sides: Measure or identify the lengths of the sides \( a \), \( b \), and \( c \).
- Calculate the perimeter: Use the formula \( P = a + b + c \) to find the perimeter.
- Calculate the area (using base and height): Use the formula \( A = \frac{1}{2}bh \) if the height is known.
- Calculate the area (using Heron's formula): If the height is not known, use Heron's formula \( A = \sqrt{s(s - a)(s - b)(s - c)} \) after calculating the semi-perimeter \( s = \frac{a + b + c}{2} \).
Example Calculation
Let's consider a triangle with sides of lengths 7 units, 8 units, and 9 units:
- Perimeter:
- Area (using Heron's formula):
\( P = 7 + 8 + 9 = 24 \) units
\( s = \frac{7 + 8 + 9}{2} = 12 \)
\( A = \sqrt{12(12 - 7)(12 - 8)(12 - 9)} = \sqrt{12 \times 5 \times 4 \times 3} = \sqrt{720} \approx 26.8 \) square units
By mastering these basic formulas and methods, you can easily determine the perimeter and area of any triangle, which is a fundamental skill in geometry.
Circle: Circumference and Area
A circle is a perfectly round shape where all points on the edge are equidistant from the center. Understanding how to calculate the circumference and area of a circle is fundamental in geometry. Below are the detailed steps to determine the circumference and area of a circle.
Circumference of a Circle
The circumference of a circle is the distance around the edge of the circle. It is equivalent to the perimeter of other shapes and can be calculated using the radius or the diameter of the circle.
- Let \( r \) represent the radius of the circle (the distance from the center to any point on the edge).
- Let \( d \) represent the diameter of the circle (twice the radius).
- The formulas for the circumference (\( C \)) of a circle are:
\( C = 2\pi r \)
or
\( C = \pi d \)
For example, if the radius \( r \) is 7 units, the circumference is calculated as:
\( C = 2\pi \times 7 = 14\pi \approx 43.98 \) units
Alternatively, if the diameter \( d \) is 14 units, the circumference is:
\( C = \pi \times 14 = 14\pi \approx 43.98 \) units
Area of a Circle
The area of a circle is the amount of space enclosed within its boundary. It is calculated using the radius of the circle.
- Let \( r \) represent the radius of the circle.
- The formula for the area (\( A \)) of a circle is:
\( A = \pi r^2 \)
For example, if the radius \( r \) is 7 units, the area is calculated as:
\( A = \pi \times 7^2 = \pi \times 49 \approx 153.94 \) square units
Step-by-Step Calculation
To ensure clarity, let's outline the steps to calculate the circumference and area of a circle:
- Determine the radius or diameter: Measure or identify the radius (\( r \)) or diameter (\( d \)) of the circle.
- Calculate the circumference: Use the formula \( C = 2\pi r \) or \( C = \pi d \) to find the circumference.
- Calculate the area: Use the formula \( A = \pi r^2 \) to find the area.
Example Calculation
Let's consider a circle with a radius of 5 units:
- Circumference:
- Area:
\( C = 2\pi \times 5 = 10\pi \approx 31.42 \) units
\( A = \pi \times 5^2 = \pi \times 25 \approx 78.54 \) square units
By mastering these basic formulas, you can easily determine the circumference and area of any circle, which is a vital skill in geometry.
Advanced Geometric Shapes
In this section, we will explore the formulas for the perimeter and area of more advanced geometric shapes such as the parallelogram, rhombus, trapezoid, ellipse, and regular polygon. Understanding these formulas can help in solving complex geometry problems and applying these shapes in real-world scenarios.
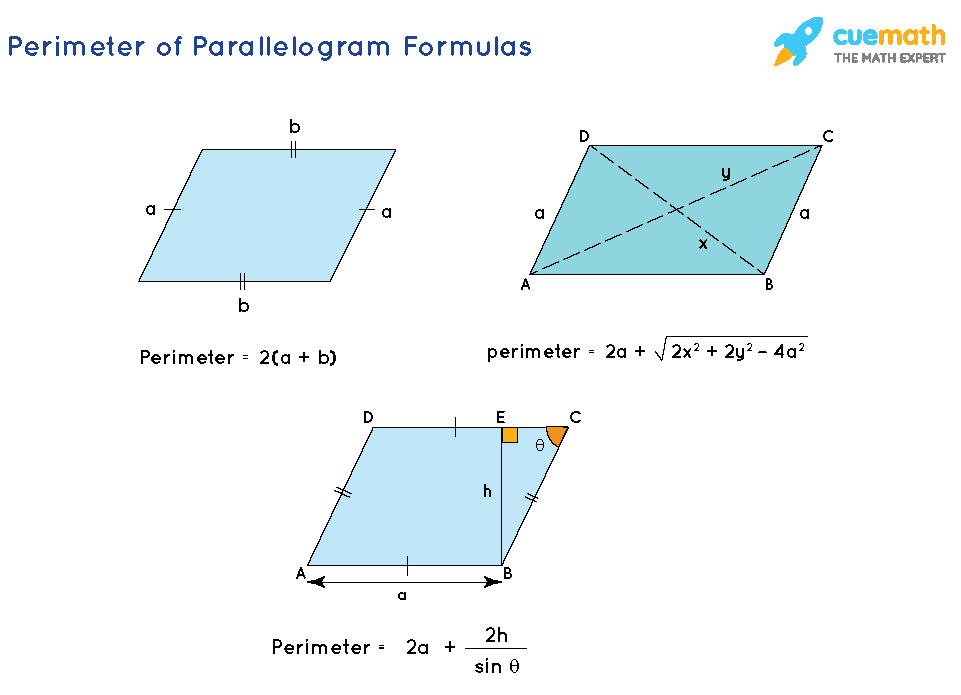
Parallelogram: Perimeter and Area
- Perimeter: The perimeter \( P \) of a parallelogram is given by the formula:
\( P = 2(a + b) \)
where \( a \) and \( b \) are the lengths of the adjacent sides. - Area: The area \( A \) of a parallelogram is given by:
\( A = b \cdot h \)
where \( b \) is the base and \( h \) is the height perpendicular to the base.
Rhombus: Perimeter and Area
- Perimeter: The perimeter \( P \) of a rhombus is given by:
\( P = 4a \)
where \( a \) is the length of a side. - Area: The area \( A \) of a rhombus is given by:
\( A = \frac{1}{2} d_1 d_2 \)
where \( d_1 \) and \( d_2 \) are the lengths of the diagonals.
Trapezoid: Perimeter and Area
- Perimeter: The perimeter \( P \) of a trapezoid is given by:
\( P = a + b + c + d \)
where \( a \), \( b \), \( c \), and \( d \) are the lengths of the sides. - Area: The area \( A \) of a trapezoid is given by:
\( A = \frac{1}{2} (a + b) h \)
where \( a \) and \( b \) are the lengths of the parallel sides and \( h \) is the height.
Ellipse: Circumference and Area
- Circumference: The circumference \( C \) of an ellipse can be approximated by:
\( C \approx \pi [3(a + b) - \sqrt{(3a + b)(a + 3b)}] \)
where \( a \) and \( b \) are the semi-major and semi-minor axes, respectively. - Area: The area \( A \) of an ellipse is given by:
\( A = \pi a b \)
where \( a \) and \( b \) are the lengths of the semi-major and semi-minor axes, respectively.
Regular Polygon: Perimeter and Area
- Perimeter: The perimeter \( P \) of a regular polygon is given by:
\( P = n s \)
where \( n \) is the number of sides and \( s \) is the length of a side. - Area: The area \( A \) of a regular polygon is given by:
\( A = \frac{1}{4} n s^2 \cot(\pi / n) \)
where \( n \) is the number of sides and \( s \) is the length of a side.
Parallelogram: Perimeter and Area
A parallelogram is a four-sided figure with opposite sides that are parallel and equal in length. Here, we will explore the formulas used to calculate the perimeter and area of a parallelogram.
Perimeter of a Parallelogram
The perimeter of a parallelogram is the sum of the lengths of all its sides. Since the opposite sides of a parallelogram are equal, the formula for the perimeter is:
\[ \text{Perimeter} = 2(a + b) \]
where \( a \) and \( b \) are the lengths of the two adjacent sides.
Area of a Parallelogram
The area of a parallelogram is calculated by multiplying the base by the height. The formula is:
\[ \text{Area} = b \times h \]
where \( b \) is the length of the base and \( h \) is the perpendicular height from the base to the opposite side.
Step-by-Step Calculation
- Identify the lengths of the base \( b \) and the height \( h \).
- Multiply the base \( b \) by the height \( h \) to find the area.
- Identify the lengths of the adjacent sides \( a \) and \( b \).
- Sum the lengths of the two adjacent sides and multiply by 2 to find the perimeter.
Example
Let's consider a parallelogram with a base \( b \) of 8 cm, height \( h \) of 5 cm, and side \( a \) of 6 cm.
- Base \( b \) = 8 cm
- Height \( h \) = 5 cm
- Adjacent side \( a \) = 6 cm
Step 1: Calculate the area:
\[ \text{Area} = b \times h = 8 \, \text{cm} \times 5 \, \text{cm} = 40 \, \text{cm}^2 \]
Step 2: Calculate the perimeter:
\[ \text{Perimeter} = 2(a + b) = 2(6 \, \text{cm} + 8 \, \text{cm}) = 2 \times 14 \, \text{cm} = 28 \, \text{cm} \]
Summary
| Formula | Calculation |
|---|---|
| Perimeter | \[ 2(a + b) \] |
| Area | \[ b \times h \] |
By understanding these formulas and following the steps outlined above, you can easily calculate the perimeter and area of any parallelogram.

Rhombus: Perimeter and Area
A rhombus is a type of quadrilateral with all four sides of equal length. It is also referred to as an equilateral quadrilateral, as all sides are congruent. A rhombus has opposite angles that are equal and diagonals that bisect each other at right angles.
Perimeter of a Rhombus
The perimeter of a rhombus can be calculated easily since all sides are of equal length. If each side of the rhombus is denoted by \( s \), then the perimeter \( P \) is given by:
\[ P = 4s \]
Where:
- \( s \) = length of one side of the rhombus
Area of a Rhombus
The area of a rhombus can be calculated using either the length of its diagonals or the base and height. Below are the two methods:
1. Using Diagonals
If \( d_1 \) and \( d_2 \) are the lengths of the diagonals of the rhombus, the area \( A \) can be found using the formula:
\[ A = \frac{1}{2} \times d_1 \times d_2 \]
Where:
- \( d_1 \) = length of the first diagonal
- \( d_2 \) = length of the second diagonal
2. Using Base and Height
If \( b \) is the length of the base and \( h \) is the height (the perpendicular distance between two opposite sides), the area \( A \) can be calculated as:
\[ A = b \times h \]
Where:
- \( b \) = length of the base
- \( h \) = height (perpendicular distance between two opposite sides)
Example Calculation
Let's consider a rhombus with each side of length 6 cm, and diagonals of lengths 8 cm and 6 cm.
- Perimeter: \( P = 4s = 4 \times 6 \, \text{cm} = 24 \, \text{cm} \)
- Area using diagonals: \( A = \frac{1}{2} \times d_1 \times d_2 = \frac{1}{2} \times 8 \, \text{cm} \times 6 \, \text{cm} = 24 \, \text{cm}^2 \)
In conclusion, understanding the perimeter and area formulas of a rhombus is essential for solving various geometric problems. By using the simple formulas provided, one can easily calculate these values for any given rhombus.
Trapezoid: Perimeter and Area
A trapezoid, also known as a trapezium in some regions, is a four-sided figure with at least one pair of parallel sides. The parallel sides are referred to as the bases of the trapezoid, while the non-parallel sides are the legs.
Perimeter of a Trapezoid
The perimeter of a trapezoid is the sum of the lengths of all its sides. If a trapezoid has sides of lengths \(a\), \(b\), \(c\), and \(d\) with \(a\) and \(b\) being the parallel sides, then the perimeter \(P\) is given by:
\[
P = a + b + c + d
\]
Area of a Trapezoid
The area of a trapezoid is calculated using the lengths of the parallel sides (bases) and the height (the perpendicular distance between the bases). If \(a\) and \(b\) are the lengths of the parallel sides and \(h\) is the height, the area \(A\) is given by:
\[
A = \frac{1}{2} (a + b) \times h
\]
Example Calculation
Consider a trapezoid with the following dimensions:
- Base 1 (\(a\)): 8 cm
- Base 2 (\(b\)): 5 cm
- Height (\(h\)): 4 cm
- Non-parallel sides (\(c\) and \(d\)): 6 cm and 7 cm
To find the perimeter:
\[
P = a + b + c + d = 8 + 5 + 6 + 7 = 26 \text{ cm}
\]
To find the area:
\[
A = \frac{1}{2} (a + b) \times h = \frac{1}{2} (8 + 5) \times 4 = \frac{1}{2} \times 13 \times 4 = 26 \text{ cm}^2
\]
Summary
- Perimeter: Sum of all four sides.
- Area: Half the sum of the lengths of the parallel sides multiplied by the height.
Understanding these formulas allows you to compute the perimeter and area of any trapezoid efficiently.
Ellipse: Circumference and Area
An ellipse is a shape that looks like a stretched circle. It has two main measurements: the semi-major axis (a) and the semi-minor axis (b).
Area of an Ellipse
The area (A) of an ellipse can be calculated using the following formula:
\[ A = \pi \times a \times b \]
- a is the length of the semi-major axis (the longest radius of the ellipse).
- b is the length of the semi-minor axis (the shortest radius of the ellipse).
Circumference of an Ellipse
Calculating the circumference (C) of an ellipse is more complex than calculating the area. There is no simple exact formula, but an approximate formula is given by:
\[ C \approx \pi \times \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \]
For a more accurate approximation, Ramanujan's formula can be used:
\[ C \approx \pi \times \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] \]
- a is the length of the semi-major axis.
- b is the length of the semi-minor axis.
Steps to Calculate the Area and Circumference
- Measure the lengths of the semi-major axis (a) and the semi-minor axis (b).
- Plug these values into the respective formulas for area and circumference.
- For the area, multiply π by the product of the semi-major and semi-minor axes.
- For the circumference, use the approximation formula or Ramanujan's formula for a more accurate result.
Understanding these formulas helps in calculating the properties of ellipses, which are useful in various fields such as astronomy, physics, and engineering.
Regular Polygon: Perimeter and Area
A regular polygon is a polygon with all sides and all angles equal. The formulas for the perimeter and area of a regular polygon depend on the number of sides (n) and the length of each side (s).
Perimeter of a Regular Polygon
The perimeter (P) of a regular polygon can be calculated using the formula:
\[ P = n \times s \]
where:
- \( n \) = number of sides
- \( s \) = length of each side
Area of a Regular Polygon
The area (A) of a regular polygon can be calculated using the formula:
\[ A = \frac{1}{4} n s^2 \cot \left( \frac{\pi}{n} \right) \]
Alternatively, if the apothem (a) is known, the area can also be calculated as:
\[ A = \frac{1}{2} P a \]
where:
- \( a \) = apothem, which is the distance from the center to the midpoint of one of its sides
Step-by-Step Calculation
- Determine the number of sides (n) of the polygon.
- Measure the length of one side (s).
- Use the formula for perimeter to find \( P = n \times s \).
- Calculate the area using either the direct formula with the side length:
\[ A = \frac{1}{4} n s^2 \cot \left( \frac{\pi}{n} \right) \]
or, if the apothem is known:\[ A = \frac{1}{2} P a \]
Example
Consider a regular hexagon (6-sided polygon) with each side of length 10 units.
Step-by-step:
- Number of sides, \( n = 6 \)
- Length of each side, \( s = 10 \) units
- Perimeter, \( P = 6 \times 10 = 60 \) units
- Using the area formula:
\[ A = \frac{1}{4} \times 6 \times 10^2 \cot \left( \frac{\pi}{6} \right) \]
\[ A = \frac{1}{4} \times 6 \times 100 \times \sqrt{3} \]
\[ A = 150 \sqrt{3} \approx 259.81 \] square units
By following these steps, you can calculate the perimeter and area of any regular polygon given the number of sides and the length of one side.

Special Cases and Complex Shapes
When dealing with special cases and complex shapes, the formulas for perimeter and area can vary significantly. These shapes often require breaking them down into simpler components or using advanced mathematical techniques. Below are some examples of how to handle these cases:
Composite Shapes
Composite shapes are made up of two or more basic geometric shapes. To find the area and perimeter of composite shapes, follow these steps:
- Divide the composite shape into simpler shapes (rectangles, triangles, circles, etc.).
- Calculate the area and perimeter of each simple shape using their respective formulas.
- Sum the areas of all the simple shapes to get the total area of the composite shape.
- Add the lengths of the outer sides of all simple shapes to get the total perimeter.
Example: To find the area and perimeter of an L-shaped figure, divide it into two rectangles, calculate their individual areas and perimeters, and then combine them appropriately.
Irregular Shapes
Irregular shapes do not have standard formulas for perimeter and area. The common methods to find these include:
- Grid Method: Overlay a grid on the shape and count the number of full and partial squares to estimate the area.
- Decomposition: Divide the shape into a set of known shapes, calculate their areas, and sum them up.
- Integration: Use integral calculus for more precise calculations of area, especially for shapes with curved boundaries.
Example: For an irregular plot of land, you might divide it into triangles and rectangles, find the area of each, and then sum these areas.
Parametric and Polar Equations
For shapes defined by parametric or polar equations, calculus is often used to determine perimeter and area. The general steps are:
- Set up the parametric or polar equations representing the shape.
- Use calculus to derive formulas for the perimeter and area.
- Integrate the derived functions over the specified range to obtain the values.
Example: To find the area of a shape described by polar coordinates, use the formula:
\[ \text{Area} = \frac{1}{2} \int_{\alpha}^{\beta} r(\theta)^2 \, d\theta \]
Fractal Shapes
Fractals are complex shapes that display self-similarity at different scales and often have non-integer dimensions. Calculating their perimeter and area involves:
- Understanding the iterative process that generates the fractal.
- Applying formulas specific to the type of fractal (e.g., Koch snowflake).
- Using concepts from fractal geometry to approximate or exactly determine their measures.
Example: The perimeter of the Koch snowflake increases with each iteration, but its area converges to a finite value.
Examples
| Shape | Area Formula | Perimeter Formula |
|---|---|---|
| Composite Rectangle and Triangle | \(A = A_{\text{rectangle}} + A_{\text{triangle}}\) | \(P = P_{\text{outer edges}}\) |
| Irregular Shape | Grid Method or Decomposition | Sum of outer edge lengths |
| Shape with Polar Coordinates | \( \frac{1}{2} \int_{\alpha}^{\beta} r(\theta)^2 \, d\theta \) | Integral of arc length formula |
| Koch Snowflake (Fractal) | Converges to finite value | Increases with iterations |
Formulas for Composite Shapes
Composite shapes, also known as compound shapes, are shapes that consist of two or more simple geometric figures. To find the perimeter and area of composite shapes, you need to break them down into simpler shapes, calculate the perimeter and area of each part, and then combine these results appropriately. Below are the steps and formulas for finding the perimeter and area of some common composite shapes.
Steps to Calculate the Perimeter of Composite Shapes
- Identify the simpler shapes that make up the composite shape.
- Calculate the perimeter of each individual shape.
- Add the lengths of the outer sides to get the total perimeter.
- Exclude any internal sides that are not part of the outer boundary.
Steps to Calculate the Area of Composite Shapes
- Identify and separate the simpler shapes within the composite shape.
- Calculate the area of each individual shape using the appropriate formulas.
- Sum the areas of all the individual shapes to get the total area.
- For complex shapes with overlapping parts, subtract the areas of the overlapping regions.
Examples and Formulas
- Example 1: Composite Shape with Rectangles and Triangles
Consider a shape that consists of a rectangle with a triangle on top.
| Rectangle Area: | \( A_{\text{rectangle}} = l \times w \) |
| Triangle Area: | \( A_{\text{triangle}} = \frac{1}{2} \times b \times h \) |
| Total Area: | \( A_{\text{total}} = A_{\text{rectangle}} + A_{\text{triangle}} \) |
| Perimeter: | Sum of all outer sides, excluding internal shared sides. |
- Example 2: Composite Shape with Circles and Rectangles
Consider a shape that consists of a rectangle with a semicircle on one end.
| Rectangle Area: | \( A_{\text{rectangle}} = l \times w \) |
| Semicircle Area: | \( A_{\text{semicircle}} = \frac{1}{2} \pi r^2 \) |
| Total Area: | \( A_{\text{total}} = A_{\text{rectangle}} + A_{\text{semicircle}} \) |
| Perimeter: | \( P_{\text{rectangle}} + P_{\text{semicircle}} - 2r \) (subtracting the shared straight edge). |
Important Notes
- Always ensure that the units are consistent when calculating the area and perimeter.
- For irregular composite shapes, consider using grid methods or approximations.
- When dealing with curves (e.g., semicircles), use the appropriate circumference formulas adjusted for the fraction of the circle.
Formulas for Irregular Shapes
Calculating the perimeter and area for irregular shapes can be more challenging compared to regular shapes. Irregular shapes do not have standard formulas like squares or circles, but there are systematic methods to find these measurements. Here are some approaches:
Perimeter of Irregular Shapes
To find the perimeter of an irregular shape, follow these steps:
- Identify and measure each side of the shape.
- Sum the lengths of all sides.
For example, if an irregular polygon has sides of lengths \(a\), \(b\), \(c\), and \(d\), the perimeter \(P\) is calculated as:
\[
P = a + b + c + d
\]
Area of Irregular Shapes
Calculating the area of irregular shapes often involves breaking the shape into smaller, regular shapes, whose areas can be calculated more easily. Here are the steps:
- Decompose the irregular shape into a combination of known shapes like triangles, rectangles, and other polygons.
- Calculate the area of each of these simpler shapes using their respective formulas.
- Sum the areas of the simpler shapes to get the total area of the irregular shape.
Example: Decomposing an Irregular Shape
Consider an irregular quadrilateral that can be split into a triangle and a rectangle:
- Step 1: Divide the shape into a triangle and a rectangle.
- Step 2: Calculate the area of the triangle (\( \frac{1}{2} \times \text{base} \times \text{height} \)).
- Step 3: Calculate the area of the rectangle (\( \text{length} \times \text{width} \)).
- Step 4: Sum the areas of the triangle and the rectangle to get the total area.
Let's say the triangle has a base of \(4\) units and a height of \(3\) units, and the rectangle has a length of \(5\) units and a width of \(2\) units:
\[
\text{Area}_{\text{triangle}} = \frac{1}{2} \times 4 \times 3 = 6 \, \text{square units}
\]
\[
\text{Area}_{\text{rectangle}} = 5 \times 2 = 10 \, \text{square units}
\]
\[
\text{Total Area} = 6 + 10 = 16 \, \text{square units}
\]
Using Coordinate Geometry
For more complex irregular shapes, especially those plotted on a coordinate plane, the area can be found using coordinate geometry techniques, such as the shoelace formula:
\[
\text{Area} = \frac{1}{2} \left| \sum_{i=1}^{n-1} (x_i y_{i+1} - y_i x_{i+1}) + (x_n y_1 - y_n x_1) \right|
\]
Here, \((x_i, y_i)\) are the coordinates of the vertices of the polygon, taken in order.
These methods provide a structured approach to finding the perimeter and area of irregular shapes, which is essential in various real-world applications such as land surveying, architecture, and more.
Applications of Perimeter and Area Formulas
The concepts of perimeter and area are fundamental in geometry and have numerous practical applications in everyday life. Here are some detailed examples of how these formulas are used:
-
Construction and Architecture
In construction, perimeter and area calculations are essential for designing and planning buildings and other structures. For example:
-
Flooring: To determine the amount of flooring material needed, the area of the floor must be calculated. If the floor is rectangular, the area can be found using \( A = l \times w \), where \( l \) is the length and \( w \) is the width.
-
Fencing: To calculate the length of fencing required to enclose a plot of land, the perimeter is used. For a rectangular plot, the perimeter is given by \( P = 2(l + w) \).
-
-
Landscaping
Landscapers use area and perimeter calculations to plan garden layouts, design paths, and install features such as pools and patios:
-
Garden Beds: To determine the amount of soil needed for a garden bed, the area of the bed is calculated. For a circular bed, the area is \( A = \pi r^2 \), where \( r \) is the radius.
-
Walkways: The length of materials required to create a walkway can be determined by calculating the perimeter of the path, especially if it follows a complex shape.
-
-
Interior Design
Interior designers use these formulas to optimize the use of space and select the right amount of materials:
-
Paint and Wallpaper: To estimate the amount of paint or wallpaper needed, the surface area of the walls must be calculated. For example, the area of a rectangular wall is found using \( A = h \times w \), where \( h \) is the height and \( w \) is the width.
-
Carpeting: To cover a floor with carpet, the floor area is calculated. For complex rooms, the total area is the sum of the areas of all individual sections.
-
-
Sports and Recreation
In sports, knowing the area and perimeter of playing fields is crucial for proper design and maintenance:
-
Fields and Courts: The area of a soccer field, basketball court, or tennis court needs to be calculated to ensure the correct dimensions are maintained. For example, the area of a rectangular basketball court is \( A = l \times w \).
-
Running Tracks: The perimeter of an athletic track is important for determining race distances and for laying out the track accurately.
-
-
Environmental Science
Environmental scientists use these measurements to study and manage natural resources:
-
Forestry: Calculating the area of forest land is essential for managing timber resources, wildlife habitats, and conservation efforts.
-
Water Bodies: The area of lakes, ponds, and rivers is calculated to monitor water quality, manage fish populations, and plan for irrigation.
-

Real-world Examples
Understanding the perimeter and area formulas for various shapes is essential for solving real-world problems. Below are some examples of how these formulas can be applied in practical situations:
1. Landscaping a Garden
Imagine you are planning to landscape a rectangular garden. The garden's length is 20 meters and the width is 10 meters.
- Perimeter: To calculate the amount of fencing needed, use the perimeter formula for a rectangle:
\[
\text{Perimeter} = 2 \times ( \text{length} + \text{width} ) = 2 \times (20 + 10) = 60 \text{ meters}
\] - Area: To determine the amount of grass seed required, use the area formula for a rectangle:
\[
\text{Area} = \text{length} \times \text{width} = 20 \times 10 = 200 \text{ square meters}
\]
2. Painting a Wall
If you need to paint a triangular wall, knowing its dimensions helps you calculate the paint needed. Suppose the wall's base is 5 meters and its height is 3 meters.
- Area: Use the area formula for a triangle:
\[
\text{Area} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 5 \times 3 = 7.5 \text{ square meters}
\]
3. Tiling a Circular Floor
For a circular floor with a radius of 4 meters, calculate the area to know how many tiles are needed.
- Area: Use the area formula for a circle:
\[
\text{Area} = \pi \times r^2 = \pi \times 4^2 = 16\pi \approx 50.27 \text{ square meters}
\]
4. Building a Composite Shape
Consider a shape composed of a rectangle and a semicircle. The rectangle is 10 meters long and 4 meters wide, and the semicircle's diameter is 4 meters.
- Area: First, calculate the areas of the rectangle and the semicircle separately, then add them together:
Rectangle:
\[
\text{Area} = \text{length} \times \text{width} = 10 \times 4 = 40 \text{ square meters}
\]Semicircle:
\[
\text{Area} = \frac{1}{2} \times \pi \times r^2 = \frac{1}{2} \times \pi \times 2^2 = 2\pi \approx 6.28 \text{ square meters}
\]Total Area:
\[
\text{Total Area} = 40 + 6.28 = 46.28 \text{ square meters}
\]
5. Installing a Fence Around a Farm
If a farmer wants to fence a trapezoidal piece of land with bases of 15 meters and 10 meters, and the height is 8 meters, they will need to calculate the perimeter and area.
- Perimeter: Use the perimeter formula for a trapezoid:
\[
\text{Perimeter} = a + b + c + d
\]
where \(a\) and \(b\) are the lengths of the two parallel sides, and \(c\) and \(d\) are the lengths of the non-parallel sides. - Area: Use the area formula for a trapezoid:
\[
\text{Area} = \frac{1}{2} \times (a + b) \times \text{height} = \frac{1}{2} \times (15 + 10) \times 8 = 100 \text{ square meters}
\]
Frequently Asked Questions (FAQ)
Here are some frequently asked questions about perimeter and area formulas:
- Why are perimeter and area important?
Perimeter and area are fundamental concepts in geometry that help us understand the properties of shapes. They are used in various real-life applications such as measuring plots of land, constructing buildings, and designing various objects.
- How do you find the area and perimeter of a square?
The area of a square is found by squaring the length of one of its sides. If the side length is \( s \), then the area \( A \) is given by:
\[ A = s^2 \]
The perimeter of a square is the sum of all its sides, which is four times the side length:
\[ P = 4s \]
- What is the formula for the area and perimeter of a rectangle?
The area of a rectangle is found by multiplying its length \( l \) by its width \( w \):
\[ A = l \times w \]
The perimeter of a rectangle is the sum of all its sides:
\[ P = 2l + 2w \]
- How do you calculate the area of a triangle?
The area of a triangle is given by the formula:
\[ A = \frac{1}{2} \times \text{base} \times \text{height} \]
Where the base is one side of the triangle and the height is the perpendicular distance from the base to the opposite vertex.
- Can you explain how to find the circumference and area of a circle?
The circumference \( C \) of a circle is found using the formula:
\[ C = 2\pi r \]
Where \( r \) is the radius of the circle. The area \( A \) of a circle is given by:
\[ A = \pi r^2 \]
- What are some real-world applications of perimeter and area formulas?
These formulas are used in many fields such as architecture, engineering, and agriculture. For example, they are crucial when designing floor plans, creating land plots, and even in everyday tasks like wrapping gifts or laying out a garden.
- Where can I find more resources on perimeter and area formulas?
Many educational websites offer comprehensive guides and practice problems for perimeter and area formulas. These resources can help deepen your understanding and improve your skills.
Tìm Chu Vi và Diện Tích của Hình Hợp | Ví Dụ Hình Chữ L | Hình Học | Toán với Mr. J
READ MORE:
Chu Vi, Diện Tích, và Thể Tích Giải Thích | Toán với Mr. J