Perimeter of Kite: The Complete Guide to Understanding and Calculating Kite Perimeter

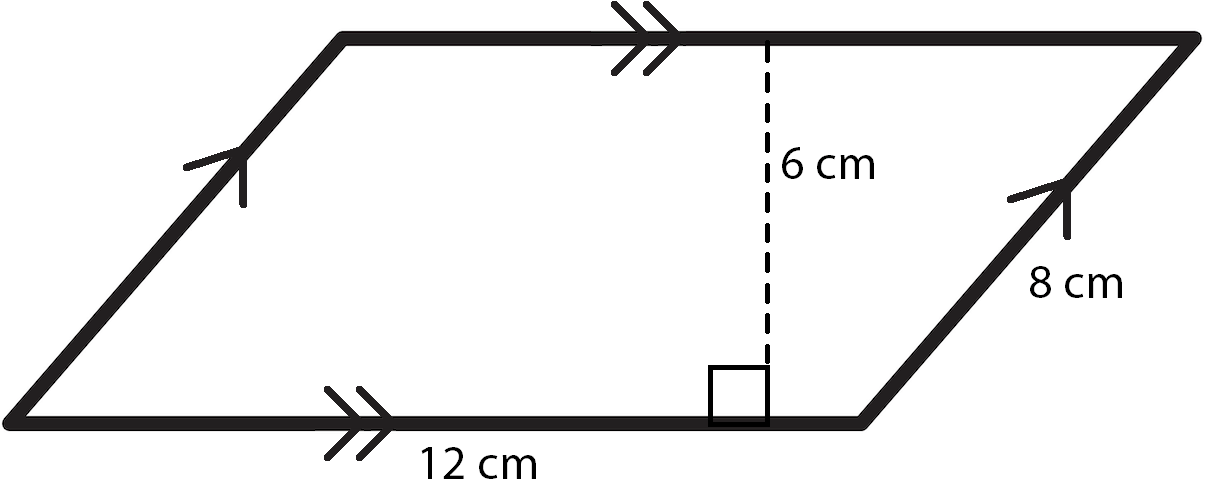
The perimeter of a kite is the total length around the kite. A kite is a quadrilateral with two distinct pairs of adjacent sides that are equal. To calculate the perimeter, you can use the lengths of these sides.

Formula

The formula for the perimeter of a kite is:

\[ P = 2(a + b) \]

Where \(a\) and \(b\) are the lengths of the two distinct pairs of adjacent sides.

Step-by-Step Calculation

1. Identify the lengths of the two pairs of adjacent sides.
2. Add the lengths of the two pairs of sides.
3. Multiply the sum by 2 to get the perimeter.

Example

Consider a kite with side lengths \(a = 5 \, \text{cm}\) and \(b = 7 \, \text{cm}\). The perimeter is calculated as follows:

\[ P = 2(a + b) = 2(5 + 7) = 2 \times 12 = 24 \, \text{cm} \]

Therefore, the perimeter of the kite is 24 cm.

Visual Representation

The diagram below illustrates a kite with sides labeled \(a\) and \(b\).

Additional Tips

• Ensure to measure all sides accurately.
• If the kite's sides are given in different units, convert them to the same unit before calculation.
• Check the properties of the kite to confirm it fits the definition before using the formula.

Understanding and using the formula for the perimeter of a kite can help solve various geometric problems related to kites.

A kite is a fascinating quadrilateral in geometry, known for its unique properties and symmetrical shape. It is defined as a quadrilateral with two distinct pairs of adjacent sides that are equal in length. This distinct shape resembles a traditional flying kite, hence the name.

In geometry, kites are important for several reasons:

• Symmetry: A kite has an axis of symmetry along one of its diagonals, which divides it into two congruent triangles.
• Angles: The angles between the unequal sides are equal. Additionally, the diagonals intersect at right angles (90 degrees).
• Diagonals: One diagonal bisects the other, creating perpendicular intersections. The longer diagonal bisects the kite into two congruent triangles.

These properties make kites a subject of interest in various geometrical studies and applications. Understanding the fundamental aspects of kites is crucial for exploring their perimeter, area, and other related geometric concepts.

A kite is a special type of quadrilateral with distinct geometric properties. By definition, a kite has two pairs of adjacent sides that are equal in length. This unique arrangement of sides gives the kite its characteristic shape and properties.

Here are the key properties of a kite:

• Sides: A kite has two pairs of adjacent sides that are equal. If we denote the lengths of these sides as \( a \) and \( b \), then each pair of adjacent sides is \( a, a \) and \( b, b \).
• Diagonals: The diagonals of a kite intersect at right angles (90 degrees). One of the diagonals bisects the other.
• Angles: The angles between the pairs of equal sides are equal. Specifically, the angles opposite the equal sides are congruent.
• Symmetry: A kite has an axis of symmetry along one of its diagonals. This diagonal divides the kite into two congruent triangles.
• Perimeter: The perimeter of a kite can be calculated using the formula: \[ P = 2(a + b) \] where \( a \) and \( b \) are the lengths of the pairs of equal sides.

These properties make kites unique and interesting shapes in the study of geometry, with various applications and theorems associated with them.

The perimeter of a kite is the total distance around the kite, which can be calculated by summing the lengths of all its sides. Given that a kite has two pairs of adjacent sides that are equal in length, calculating its perimeter becomes straightforward.

To understand how to find the perimeter of a kite, follow these steps:

1. Identify the lengths of the pairs of equal sides: Let the lengths of one pair of equal sides be \( a \) and the lengths of the other pair be \( b \).
2. Sum the lengths of all sides: Since there are two pairs of equal sides, the total perimeter \( P \) is the sum of these lengths: \[ P = a + a + b + b \]
3. Simplify the expression: Combine the lengths of the sides to get the formula for the perimeter: \[ P = 2a + 2b \]
4. Factor out the common factor: To further simplify, factor out the common factor of 2: \[ P = 2(a + b) \]

Therefore, the formula for the perimeter of a kite is:
\[
P = 2(a + b)
\]
where \( a \) and \( b \) are the lengths of the pairs of equal sides. This formula makes it easy to calculate the perimeter if you know the lengths of the sides.

Understanding this formula allows for quick and accurate calculation of the perimeter, which is essential for solving various geometric problems involving kites.

The perimeter of a kite is a measure of the total length around the shape. Since a kite is characterized by having two pairs of adjacent sides that are equal in length, calculating its perimeter is straightforward with the appropriate formula.

Here is the step-by-step process to derive and use the perimeter formula for a kite:

1. Identify the side lengths: Let the lengths of the two pairs of equal sides be \( a \) and \( b \). This means there are two sides of length \( a \) and two sides of length \( b \).
2. Sum the lengths of all sides: The perimeter \( P \) is the sum of these four sides. Therefore, the perimeter can be expressed as: \[ P = a + a + b + b \]
3. Simplify the expression: Combine the lengths of the sides to simplify the expression: \[ P = 2a + 2b \]
4. Factor out the common factor: To further simplify, factor out the common factor of 2 from the expression: \[ P = 2(a + b) \]

Thus, the perimeter formula for a kite is:
\[
P = 2(a + b)
\]
where \( a \) and \( b \) are the lengths of the pairs of adjacent equal sides.

This formula is useful for quickly calculating the perimeter of a kite when you know the lengths of its sides. It highlights the simplicity of the relationship between the side lengths and the perimeter, making it easy to apply in various geometric problems.

Calculating the perimeter of a kite involves a straightforward process. Follow these step-by-step instructions to find the perimeter using the lengths of the sides.

1. Identify the side lengths: Determine the lengths of the pairs of adjacent sides of the kite. Let these lengths be \( a \) and \( b \), where \( a \) and \( b \) represent the lengths of the equal sides.
2. Write down the perimeter formula: Recall that the formula for the perimeter \( P \) of a kite is: \[ P = 2(a + b) \]
3. Plug in the side lengths: Substitute the given side lengths \( a \) and \( b \) into the formula. For example, if \( a = 5 \) units and \( b = 7 \) units, the formula becomes: \[ P = 2(5 + 7) \]
4. Perform the addition inside the parentheses: Add the lengths of the sides inside the parentheses: \[ 5 + 7 = 12 \]
5. Multiply by 2: Finally, multiply the sum by 2 to find the perimeter: \[ P = 2 \times 12 = 24 \]

Therefore, the perimeter of the kite is 24 units. This step-by-step method ensures that you accurately calculate the perimeter by following a logical sequence of operations.

By using this approach, you can easily find the perimeter of any kite as long as you know the lengths of its sides.

To solidify your understanding of the perimeter of a kite, let's go through some examples and practice problems.

Example 1

Given a kite with sides of lengths 5 cm, 5 cm, 7 cm, and 7 cm, find the perimeter of the kite.

1. Identify the lengths of the sides: 5 cm, 5 cm, 7 cm, and 7 cm.
2. Add the lengths of all the sides:
   • Perimeter = 5 cm + 5 cm + 7 cm + 7 cm
3. Calculate the sum:
   • Perimeter = 24 cm

The perimeter of the kite is 24 cm.

Example 2

A kite has two pairs of equal sides. One pair of sides is 8 inches each, and the other pair is 6 inches each. Calculate the perimeter of the kite.

1. Identify the lengths of the sides: 8 inches, 8 inches, 6 inches, and 6 inches.
2. Add the lengths of all the sides:
   • Perimeter = 8 inches + 8 inches + 6 inches + 6 inches
3. Calculate the sum:
   • Perimeter = 28 inches

The perimeter of the kite is 28 inches.

Practice Problems

Try solving these problems on your own:

1. A kite has side lengths of 9 cm, 9 cm, 12 cm, and 12 cm. What is the perimeter of the kite?
2. Find the perimeter of a kite with sides of 10 m, 10 m, 15 m, and 15 m.
3. Calculate the perimeter of a kite where each pair of equal sides measures 7.5 inches and 5.5 inches respectively.
4. A kite's sides are 6.2 cm, 6.2 cm, 4.8 cm, and 4.8 cm. Determine the perimeter.
5. Given a kite with side lengths 11 cm, 11 cm, 8 cm, and 8 cm, find the perimeter.

Check your answers:

• Problem 1: 42 cm
• Problem 2: 50 m
• Problem 3: 26 inches
• Problem 4: 22 cm
• Problem 5: 38 cm

Detailed Solution to a Practice Problem

Let's solve problem 2 step-by-step:

1. Identify the side lengths: 10 m, 10 m, 15 m, and 15 m.
2. Add the lengths of all sides:
   • Perimeter = 10 m + 10 m + 15 m + 15 m
3. Calculate the sum:
   • Perimeter = 50 m

The perimeter of the kite is 50 m.

The concept of the perimeter of a kite has several practical applications in various fields. Understanding these applications helps in appreciating the importance of geometric principles in everyday activities.

• Construction and Architecture

  In construction, the perimeter of kite-shaped plots or sections is crucial for determining the amount of materials required. For example, if a park or a section of a building has a kite shape, knowing its perimeter helps in planning the boundaries and calculating the fencing materials needed. This ensures that the resources are utilized efficiently without wastage.

• Gardening and Landscaping

  When planning gardens or landscaped areas, the perimeter is used to outline the boundaries. For instance, if a garden bed is designed in the shape of a kite, calculating the perimeter helps in determining the length of the edging material required to enclose it. This is vital for both aesthetic purposes and functionality, such as keeping soil and plants contained.

• Surveying and Land Measurement

  Surveyors often encounter kite-shaped land plots. Calculating the perimeter of these plots is essential for defining property boundaries and for legal documentation. Accurate measurements ensure clear demarcation, preventing disputes between neighboring properties.

• Art and Design

  In art and design, especially in creating patterns and decorative elements, understanding the perimeter of kite shapes can influence the design process. Artists and designers use these measurements to ensure symmetry and balance in their creations, whether in paintings, sculptures, or graphic designs.

• Manufacturing and Fabrication

  Manufacturers often need to cut materials into specific shapes, including kites. Knowing the perimeter helps in determining the amount of material needed and in planning the cutting process to minimize waste. This is particularly important in industries like textile manufacturing, where precision is key.

• Sports and Recreation

  In designing sports fields and recreational areas, kite shapes might be used for various sections. Calculating the perimeter helps in planning the layout and ensuring that the dimensions meet regulatory standards. This ensures fair play and optimal use of space.

Calculating the perimeter of a kite can be straightforward if you apply the correct steps and avoid common pitfalls. Here are some typical mistakes and how you can steer clear of them:

• Confusing Side Lengths:

  A kite has two pairs of adjacent sides that are of different lengths. Make sure to correctly identify and pair the sides before calculating the perimeter. The formula for the perimeter is:

  \( \text{Perimeter} = 2(a + b) \)

  where \(a\) and \(b\) are the lengths of the two pairs of sides.

• Incorrect Formula Application:

  Sometimes, students forget to double the sum of the pairs of sides. Always remember to use the formula correctly:

  \( \text{Perimeter} = 2(a + b) \)

• Measurement Errors:

  Inaccurate measurement of the sides can lead to incorrect perimeter calculations. Ensure that your measurements are precise and double-check if necessary.

• Arithmetic Mistakes:

  Simple arithmetic errors can easily occur. Carefully perform addition and multiplication steps to avoid these mistakes.

• Overlooking Units:

  Using inconsistent units throughout the calculation can result in incorrect values. Always ensure all measurements are in the same unit.

By being mindful of these common mistakes, you can greatly improve the accuracy of your kite perimeter calculations.

Kites are fascinating geometric shapes with a variety of unique properties and applications. In this section, we will explore advanced topics related to kites, including their relationships with other quadrilaterals, special properties, and theorems.

1. Relationships with Other Quadrilaterals

• Rhombus: A kite can be considered a special type of rhombus if all four sides are of equal length. This also makes the kite a special case of a parallelogram.
• Darts: A concave kite is often referred to as a dart, where one internal angle is greater than 180 degrees.
• Parallelograms: While a kite has two pairs of adjacent sides that are equal, a parallelogram has two pairs of opposite sides that are equal and parallel. Some kites can also be parallelograms if they have equal-length sides.

2. Special Properties of Kites

• Perpendicular Diagonals: The diagonals of a kite intersect at right angles (90 degrees).
• Diagonal Bisectors: One diagonal bisects the other, dividing it into two equal parts.
• Congruent Triangles: One of the diagonals divides the kite into two congruent triangles.
• Angle Bisectors: One of the diagonals bisects a pair of opposite angles.

3. Theorems Related to Kites

• Kite Diagonal Theorem: If a quadrilateral is a kite, its diagonals are perpendicular to each other.
• Kite Angle Theorem: If a quadrilateral is a kite, it has one pair of opposite angles that are congruent.
• Kite Congruent Triangles Theorem: If a quadrilateral is a kite, one of its diagonals divides it into two congruent triangles.
• Kite Diagonal Bisector Theorem: If a quadrilateral is a kite, one of its diagonals bisects the other diagonal.

4. Practical Applications of Kite Properties

Kites have practical applications in various fields, including engineering, architecture, and even kite flying. Understanding the geometric properties of kites can help in designing structures and understanding the stress and forces acting on materials.

For example, the property of perpendicular diagonals is utilized in certain architectural designs to ensure stability and equal distribution of forces. In aerodynamics, the study of kites can help in understanding lift and drag forces, which are crucial in designing efficient flying objects.

Exploring these advanced topics not only deepens our understanding of kites but also showcases their relevance in real-world applications.

Visual representations and diagrams are essential tools for understanding the geometry of a kite and its perimeter. Here are some useful visual aids and step-by-step guides to help grasp these concepts:

1. Basic Kite Diagram

A basic diagram of a kite typically shows two pairs of adjacent sides of equal length. This symmetry helps in identifying the properties of the kite.

• Draw a kite with vertices labeled \( A, B, C, \) and \( D \).
• Ensure \( AB = AD \) and \( BC = CD \).

2. Perimeter Calculation

To calculate the perimeter, add the lengths of all sides. Use the formula:

\[
P = 2(a + b)
\]
where \( a \) and \( b \) are the lengths of the pairs of equal sides.

3. Diagonal Intersection

The diagonals of a kite intersect at right angles, dividing it into four right triangles. This can be visually represented as:

4. Step-by-Step Guide to Drawing a Kite

1. Start by drawing one diagonal.
2. Draw the second diagonal perpendicular to the first, intersecting at the midpoint.
3. Connect the endpoints of the diagonals to form the kite shape.

5. Example Problem with Diagram

Given a kite with sides \( a = 5 \) cm and \( b = 7 \) cm, find its perimeter.

• Use the formula: \( P = 2(a + b) \)
• Substitute the values: \( P = 2(5 + 7) = 2 \times 12 = 24 \) cm

6. Interactive Tools

Use interactive geometry tools and software to visualize and manipulate kites dynamically. These tools allow you to change side lengths and angles to see how the perimeter is affected.

7. Additional Diagrams

Explore more complex kite configurations and their properties through additional diagrams and interactive models.

These visual aids and diagrams provide a comprehensive understanding of the geometry and perimeter of kites, making it easier to grasp the concepts and apply them in various problems.

• What is the perimeter of a kite?

  The perimeter of a kite is the total distance around its edges. It is calculated by adding the lengths of all four sides. The formula for the perimeter of a kite is \( P = 2(a + b) \), where \( a \) and \( b \) are the lengths of the pairs of adjacent sides.

• How do you find the perimeter of a kite?

  To find the perimeter of a kite, use the formula \( P = 2(a + b) \). Measure the lengths of one pair of adjacent sides (a and b), add them together, and then multiply by 2. For example, if a kite has sides of lengths 5 cm and 7 cm, the perimeter is \( 2(5 + 7) = 24 \) cm.

• Can the perimeter of a kite be found using its diagonals?

  Yes, if the lengths of the diagonals are known, you can use the Pythagorean theorem to find the side lengths first, and then use the perimeter formula. For a kite with diagonals of lengths \( d_1 \) and \( d_2 \), the side lengths can be found as follows:
  
  
  

  
  
  1. Divide each diagonal in half to get two segments for each diagonal.
  
  
  2. Use the Pythagorean theorem to find the lengths of the sides. For example, if the diagonals are 8 cm and 6 cm, the half-diagonals are 4 cm and 3 cm. Each side length can be calculated as \( \sqrt{(4^2 + 3^2)} = \sqrt{25} = 5 \) cm.
  
  
  3. Finally, apply the perimeter formula: \( P = 2(a + b) \). For our example, \( P = 2(5 + 5) = 20 \) cm.
  
  
  
  


• What is a common mistake when calculating the perimeter of a kite?

  A common mistake is forgetting that a kite has two pairs of equal adjacent sides. Ensure you measure the correct pairs of sides and use the formula \( P = 2(a + b) \) accurately. Another mistake is incorrectly identifying the lengths of the sides when using diagonals, leading to incorrect calculations.

• Why is the kite considered a quadrilateral?

  A kite is considered a quadrilateral because it has four sides. Specifically, it has two pairs of adjacent sides that are equal in length. This unique property distinguishes it from other types of quadrilaterals like squares or rectangles.

• Are the diagonals of a kite equal?

  No, the diagonals of a kite are not equal. One diagonal is usually longer than the other. Additionally, the diagonals intersect at right angles (90 degrees) and the longer diagonal bisects the shorter one.

In conclusion, understanding the perimeter of a kite is essential in both academic and practical applications of geometry. The unique properties of a kite, such as its distinct pairs of adjacent sides and symmetrical diagonals, make it an interesting shape to study.

By mastering the perimeter formula, $P=2(a+b)$, where a and b are the lengths of the kite's pairs of adjacent sides, one can easily calculate the perimeter of any kite. This formula is derived from the basic definition of perimeter as the total distance around a shape, and it simplifies the process for kites due to their specific properties.

Step-by-step calculations help in reinforcing the concept and ensuring accuracy in determining the perimeter. It is also beneficial to engage with various examples and practice problems to build a solid understanding. Such practice not only enhances problem-solving skills but also prepares one for more advanced geometric topics.

Real-life applications of calculating the perimeter of a kite include tasks in engineering, design, and architecture, where precise measurements are crucial. Recognizing common mistakes, such as incorrectly identifying the sides or misapplying the formula, is important to avoid errors.

Visual representations and diagrams are invaluable tools for comprehending the geometric properties of kites and the calculation of their perimeters. These visuals aid in conceptualizing the shape and the relationships between its sides and angles.

In summary, the study of the perimeter of a kite is a fundamental aspect of geometry that extends to various practical fields. By thoroughly understanding the properties, formula, and calculation steps, along with engaging in practice and visual learning, one can confidently solve perimeter-related problems involving kites.