Topic what is the perimeter of kite wxyz: Discover the simple formula to calculate the perimeter of kite WXYZ and understand its geometric properties. This comprehensive guide will provide you with step-by-step instructions, practical examples, and useful tips to master the concept of kite perimeter. Perfect for students, educators, and geometry enthusiasts looking to enhance their knowledge.
Table of Content
- Perimeter of Kite WXYZ
- Introduction to Kites in Geometry
- Definition and Properties of a Kite
- Basic Geometric Characteristics
- Understanding Side Lengths
- Formulas for Calculating Perimeter
- Step-by-Step Calculation Process
- Example Problems and Solutions
- Common Mistakes to Avoid
- Applications of Kites in Real Life
- Advanced Topics in Kite Geometry
- Practice Problems
- Summary and Key Takeaways
- Frequently Asked Questions
- YOUTUBE: Hướng dẫn tính chu vi và diện tích của hình thoi, hình thang và hình diều bằng tiếng Việt. Video giải thích chi tiết và dễ hiểu để thu hút người xem.
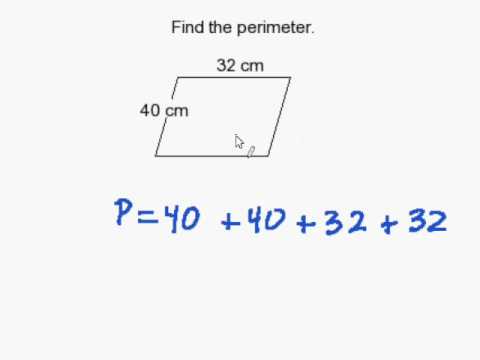
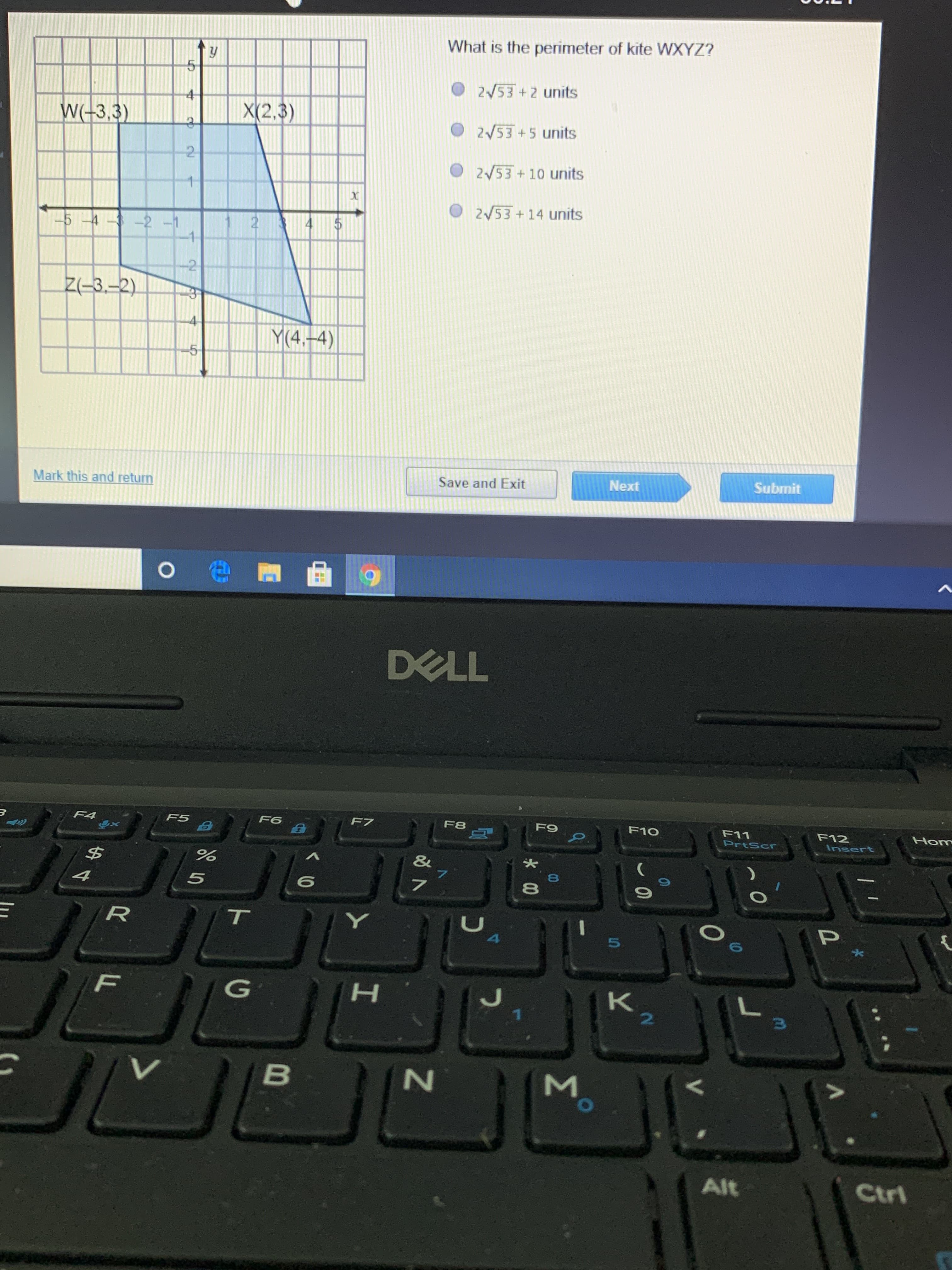
Perimeter of Kite WXYZ
The perimeter of a kite can be calculated using the lengths of its sides. A kite is a quadrilateral with two distinct pairs of adjacent sides that are equal. In kite WXYZ, let's denote the lengths of the pairs of equal sides as follows:
- Side lengths \( WX \) and \( XY \) are equal and denoted as \( a \).
- Side lengths \( YZ \) and \( ZW \) are equal and denoted as \( b \).
The formula to find the perimeter of the kite is:
\[
\text{Perimeter} = 2a + 2b
\]
Example Calculation
Suppose the lengths of the sides are given as:
- \( a = 5 \) units
- \( b = 7 \) units
Then, the perimeter of kite WXYZ can be calculated as follows:
\[
\text{Perimeter} = 2 \times 5 + 2 \times 7 = 10 + 14 = 24 \text{ units}
\]
Thus, the perimeter of kite WXYZ is 24 units.
General Formula
In general, if the side lengths \( a \) and \( b \) are known, the perimeter can always be found using the formula:
\[
\text{Perimeter} = 2a + 2b
\]
This formula is valid for any kite, regardless of the specific lengths of its sides.
READ MORE:
Introduction to Kites in Geometry
A kite is a special type of quadrilateral with unique geometric properties. In geometry, understanding the characteristics of kites is essential for solving various problems related to their shape, area, and perimeter. Kites are defined by the following properties:
- Two pairs of adjacent sides are of equal length.
- One pair of opposite angles are equal.
- The diagonals of a kite intersect at right angles (90 degrees).
- One of the diagonals bisects the other.
The sides and angles of a kite contribute to its distinct shape, which resembles the traditional flying kite. To better understand kites, let’s explore their properties and how to calculate the perimeter of kite WXYZ.
Consider a kite WXYZ with the following sides:
- \( WX = XY = a \)
- \( YZ = ZW = b \)
The perimeter of kite WXYZ is calculated by summing the lengths of all its sides. The formula for the perimeter \( P \) is given by:
\[
P = 2a + 2b
\]
To illustrate this, let's assume:
- Side lengths \( a = 5 \) units
- Side lengths \( b = 7 \) units
Using the formula, the perimeter \( P \) of kite WXYZ is:
\[
P = 2 \times 5 + 2 \times 7 = 10 + 14 = 24 \text{ units}
\]
This introduction provides a foundation for understanding kites in geometry. With these basics, we can delve deeper into more complex aspects and applications of kites in mathematical problems.
Definition and Properties of a Kite
A kite is a type of quadrilateral that has two distinct pairs of adjacent sides that are equal in length. This unique property gives the kite its characteristic shape. Here are the detailed properties of a kite:
- Two pairs of adjacent sides are equal: In kite WXYZ, sides \( WX \) and \( XY \) are equal, and sides \( YZ \) and \( ZW \) are equal. If \( WX = XY = a \) and \( YZ = ZW = b \), the kite has sides of lengths \( a \) and \( b \).
- Diagonals intersect at right angles: The diagonals of a kite intersect each other at a 90-degree angle, forming right angles at the intersection point.
- One pair of opposite angles are equal: The angles between the unequal sides are equal. For kite WXYZ, if \( \angle WXZ \) and \( \angle WYZ \) are the angles between the unequal sides, then \( \angle WXZ = \angle WYZ \).
- Diagonals bisect each other: One of the diagonals bisects the other. In kite WXYZ, if \( \overline{WY} \) and \( \overline{XZ} \) are the diagonals, then \( \overline{WY} \) bisects \( \overline{XZ} \) at a right angle.
These properties make kites a fascinating study in geometry. The symmetry and unique angle properties help in solving various geometric problems, especially those involving area and perimeter calculations.
To calculate the perimeter of kite WXYZ, the formula used is:
\[
\text{Perimeter} = 2a + 2b
\]
Where \( a \) and \( b \) are the lengths of the pairs of equal sides. For example, if \( a = 5 \) units and \( b = 7 \) units, the perimeter \( P \) would be:
\[
P = 2 \times 5 + 2 \times 7 = 10 + 14 = 24 \text{ units}
\]
Understanding these properties and definitions is crucial for mastering geometric concepts related to kites and applying them effectively in various mathematical contexts.
Basic Geometric Characteristics
A kite is a unique quadrilateral with specific geometric characteristics that distinguish it from other types of quadrilaterals. These characteristics include the lengths of its sides, its angles, and the properties of its diagonals. Here are the basic geometric characteristics of a kite:
- Equal Adjacent Sides: A kite has two pairs of adjacent sides that are equal in length. For kite WXYZ, sides \( WX \) and \( XY \) are equal, and sides \( YZ \) and \( ZW \) are equal. This can be expressed as: \[ WX = XY = a \quad \text{and} \quad YZ = ZW = b \]
- Diagonals: The diagonals of a kite intersect at right angles (90 degrees). One diagonal bisects the other. For kite WXYZ, let the diagonals be \( \overline{WY} \) and \( \overline{XZ} \). They intersect at a right angle and one diagonal bisects the other.
- Angles: A kite has one pair of opposite angles that are equal. These are the angles between the unequal sides. In kite WXYZ, if \( \angle WXZ \) and \( \angle WYZ \) are the angles between the unequal sides, then: \[ \angle WXZ = \angle WYZ \]
- Symmetry: A kite is symmetrical along one of its diagonals. This diagonal is the line of symmetry, dividing the kite into two congruent triangles.
- Area: The area of a kite can be calculated using its diagonals. If \( d_1 \) and \( d_2 \) are the lengths of the diagonals, the area \( A \) is given by: \[ A = \frac{1}{2} d_1 d_2 \]
Understanding these basic geometric characteristics is crucial for solving problems related to kites, including finding the perimeter. The perimeter of kite WXYZ can be calculated by summing the lengths of all its sides:
\[
\text{Perimeter} = 2a + 2b
\]
For example, if the lengths of the sides are \( a = 5 \) units and \( b = 7 \) units, the perimeter \( P \) is:
\[
P = 2 \times 5 + 2 \times 7 = 10 + 14 = 24 \text{ units}
\]
These characteristics not only help in identifying and distinguishing kites but also provide a foundation for further exploration of their properties and applications in geometry.
Understanding Side Lengths
In kite geometry, it is essential to understand the properties and characteristics of the side lengths. A kite is a quadrilateral with two distinct pairs of adjacent sides that are equal in length. This unique configuration defines the shape and properties of the kite.
Let's denote the side lengths of a kite as follows:
- a - The length of one pair of adjacent equal sides
- b - The length of the other pair of adjacent equal sides
Thus, if we consider kite WXYZ, the side lengths can be represented as:
- WX = XY = a
- YZ = WZ = b
Properties of the Side Lengths
- Equality in Pairs: In a kite, each pair of adjacent sides are of equal length. Therefore, WX equals XY and YZ equals WZ.
- Diagonals: The diagonals of a kite intersect at right angles and one of the diagonals bisects the other. This property is useful in solving various geometric problems related to kites.
Visual Representation
To visualize these properties, consider the following diagram of kite WXYZ:
 |
Formulas Involving Side Lengths
The perimeter of a kite can be easily calculated using the lengths of its sides. The formula for the perimeter (P) is given by:
\[ P = 2(a + b) \]
Where:
- a is the length of one pair of equal sides.
- b is the length of the other pair of equal sides.
Example Calculation
Consider a kite with side lengths 5 cm and 7 cm. Using the perimeter formula, we can calculate the perimeter as follows:
- Identify the side lengths: \( a = 5 \, \text{cm} \) and \( b = 7 \, \text{cm} \)
- Substitute the values into the formula: \( P = 2(5 + 7) \)
- Calculate the sum inside the parentheses: \( 5 + 7 = 12 \)
- Multiply by 2: \( 2 \times 12 = 24 \)
Therefore, the perimeter of the kite is 24 cm.
Common Mistakes to Avoid
- Incorrect Pair Identification: Ensure you correctly identify the pairs of equal sides to avoid miscalculations.
- Formula Application: Always use the correct formula for the perimeter, and verify your calculations.
Understanding the side lengths and their properties is crucial for solving problems related to kites in geometry. By following the outlined steps and utilizing the given formulas, you can accurately determine various characteristics of a kite.
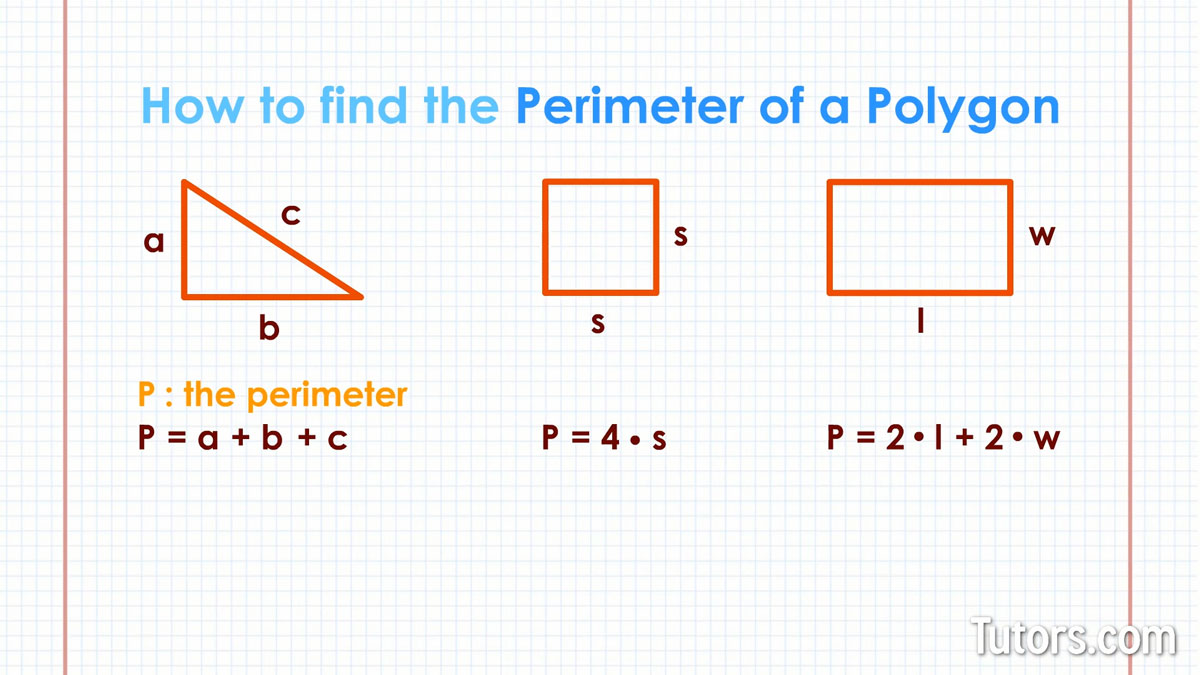
Formulas for Calculating Perimeter
The perimeter of a kite can be calculated using the formula that involves the lengths of its sides. A kite has two pairs of equal adjacent sides. If we denote the lengths of these pairs as \( a \) and \( b \), the formula for the perimeter \( P \) of the kite is:
\( P = 2(a + b) \)
Here's how to apply this formula step by step:
- Identify the lengths of the two pairs of equal sides. Let's denote them as \( a \) and \( b \).
- Add the lengths of these two pairs: \( a + b \).
- Multiply the sum by 2 to get the perimeter: \( P = 2(a + b) \).
Let's consider a few examples to illustrate this:
Example 1
A kite has side lengths of 12 inches and 15 inches for each pair of equal sides. To find the perimeter:
- Given: \( a = 12 \) inches, \( b = 15 \) inches
- Sum of side lengths: \( 12 + 15 = 27 \)
- Perimeter: \( P = 2 \times 27 = 54 \) inches
Thus, the perimeter of the kite is 54 inches.
Example 2
Consider a kite where the sides are in the ratio 3:5, and the shorter side is 24 inches. To find the perimeter:
- Given: \( a = 24 \) inches, and the ratio \( a:b = 3:5 \)
- Find \( b \): \( b = 24 \times \frac{5}{3} = 40 \) inches
- Sum of side lengths: \( 24 + 40 = 64 \)
- Perimeter: \( P = 2 \times 64 = 128 \) inches
Thus, the perimeter of the kite is 128 inches.
By following these steps and using the formula \( P = 2(a + b) \), you can easily calculate the perimeter of any kite as long as you know the lengths of its sides.
Step-by-Step Calculation Process
To calculate the perimeter of a kite, you need to follow a series of steps. This process will guide you through understanding the kite's properties, identifying the lengths of its sides, and applying the appropriate formula.
-
Identify the Lengths of the Sides:
A kite has two pairs of adjacent sides that are equal in length. Let the lengths of these sides be denoted as \(a\) and \(b\). For example, if one pair of sides each has a length of 10 cm and the other pair each has a length of 15 cm, then:
- \(a = 10 \, \text{cm}\)
- \(b = 15 \, \text{cm}\)
-
Apply the Perimeter Formula:
The formula to calculate the perimeter (\(P\)) of a kite is:
\[ P = 2(a + b) \]
Where \(a\) and \(b\) are the lengths of the pairs of equal sides.
-
Substitute the Values and Solve:
Using the values identified, substitute \(a\) and \(b\) into the formula. For example, with \(a = 10 \, \text{cm}\) and \(b = 15 \, \text{cm}\):
\[ P = 2(10 \, \text{cm} + 15 \, \text{cm}) \]
Simplify inside the parentheses first:
\[ P = 2(25 \, \text{cm}) \]
Then multiply:
\[ P = 50 \, \text{cm} \]
-
Verify Your Calculation:
Ensure all steps are followed correctly and verify by re-checking your calculations. This helps avoid errors and confirms the accuracy of your result.
By following these steps, you can accurately calculate the perimeter of any kite given the lengths of its sides. This process emphasizes understanding the kite's properties and correctly applying mathematical formulas.
Example Problems and Solutions
Understanding how to calculate the perimeter of a kite can be reinforced through example problems. Here are a few to help solidify the concept:
Example 1
Problem: A kite has its equal sides as 12 inches and 15 inches, respectively. Find its perimeter.
Solution:
- Identify the lengths of the sides. Let \(a = 12\) inches and \(b = 15\) inches.
- Use the perimeter formula for a kite: \(P = 2(a + b)\).
- Substitute the values into the formula: \(P = 2(12 + 15)\).
- Simplify the expression: \(P = 2 \times 27 = 54\) inches.
Answer: The perimeter of the kite is 54 inches.
Example 2
Problem: The sides of a kite are in the ratio of 3:5. If the smaller side is 24 inches, find its perimeter.
Solution:
- Given: \(a = 24\) inches and the ratio \(a:b = 3:5\).
- Find \(b\): \(b = 24 \times \frac{5}{3} = 40\) inches.
- Use the perimeter formula: \(P = 2(a + b)\).
- Substitute the values: \(P = 2(24 + 40)\).
- Simplify the expression: \(P = 2 \times 64 = 128\) inches.
Answer: The perimeter of the kite is 128 inches.
Example 3
Problem: A kite has side lengths of 15 inches and 18 inches. Determine its perimeter.
Solution:
- Let \(a = 15\) inches and \(b = 18\) inches.
- Use the perimeter formula: \(P = 2(a + b)\).
- Substitute the values: \(P = 2(15 + 18)\).
- Simplify the expression: \(P = 2 \times 33 = 66\) inches.
Answer: The perimeter of the kite is 66 inches.
Example 4
Problem: Jacob's kite has a perimeter of 70 inches. One pair of equal sides measures 12 inches each. Find the length of the other pair of equal sides.
Solution:
- Given: Perimeter \(P = 70\) inches and one side \(a = 12\) inches.
- Use the perimeter formula: \(P = 2(a + b)\).
- Rearrange to find \(b\): \(35 = 12 + b \Rightarrow b = 35 - 12 = 23\) inches.
Answer: The other pair of equal sides is 23 inches each.
These examples illustrate the application of the perimeter formula \(P = 2(a + b)\) for different scenarios involving kites. Practice with different values to strengthen your understanding.
Common Mistakes to Avoid
When calculating the perimeter of a kite, there are several common mistakes that can lead to incorrect results. Awareness of these pitfalls is crucial for accurate calculations. Here are some of the most frequent errors and how to avoid them:
-
Confusing Side Lengths:
One common mistake is mixing up the lengths of the different pairs of sides. Remember, a kite has two pairs of adjacent sides that are of different lengths. Ensure you correctly identify and use these pairs in your calculations.
-
Incorrect Formula Application:
Another frequent error is misapplying the formula by not doubling the lengths of both pairs of sides. The correct formula for the perimeter of a kite is \( P = 2(a + b) \), where \( a \) and \( b \) are the lengths of the two distinct pairs of sides. Always double-check that you have applied this formula correctly.
-
Measurement Errors:
Inaccurate measurement of side lengths can significantly affect the perimeter calculation. Always double-check your measurements to ensure accuracy. Using precise tools and methods can help reduce measurement errors.
-
Arithmetic Mistakes:
Simple arithmetic errors can lead to incorrect perimeter values. Carefully perform each step of addition and multiplication, and consider verifying your results with a calculator to avoid these mistakes.
-
Overlooking Units:
Failing to use consistent units throughout the calculation can result in incorrect perimeter values. Ensure that all measurements are in the same unit before performing your calculations.
By being mindful of these common mistakes, you can greatly improve the accuracy of your kite perimeter calculations, whether for academic purposes or practical applications.
Applications of Kites in Real Life
Kites are not only fascinating geometric shapes but also have various practical applications in everyday life. Below are some key areas where kites are utilized:
-
Recreational Activities:
One of the most common uses of kites is in recreational activities. People of all ages enjoy flying kites, which come in various shapes and sizes. Kite flying can be a fun outdoor activity that promotes physical exercise and enjoyment of nature.
-
Aerodynamics and Meteorology:
Kites are used in scientific research, particularly in the study of aerodynamics and meteorology. Researchers use kites to gather atmospheric data, such as wind speed and direction, temperature, and humidity at different altitudes.
-
Architecture and Engineering:
The geometric principles of kites are applied in architecture and engineering. The structural integrity and unique properties of kites make them useful in designing buildings, bridges, and other structures. The kite shape can provide stability and aesthetic appeal in architectural designs.
-
Renewable Energy:
Kite power systems are an innovative application in the field of renewable energy. These systems harness wind energy by using kites to drive generators, providing a sustainable and eco-friendly source of power. Kite energy systems can operate at higher altitudes where winds are stronger and more consistent.
-
Education:
Kites are used as educational tools to teach students about geometry, physics, and engineering concepts. Building and flying kites can help students understand principles such as symmetry, angles, force, and lift, making learning more interactive and engaging.
Overall, the versatility and unique characteristics of kites make them valuable in various fields, demonstrating their importance beyond just recreational use.
Advanced Topics in Kite Geometry
In advanced studies of kite geometry, we explore deeper properties and applications that extend beyond the basic definitions and calculations. Below are some of the advanced topics related to kites:
- Diagonal Properties: The diagonals of a kite are perpendicular and bisect each other at right angles. This property can be used to derive various geometric proofs and solve complex problems involving kites.
- Symmetry and Congruence: Kites exhibit reflective symmetry along the axis that contains the longer diagonal. Understanding this symmetry can aid in solving problems related to transformations and congruence of geometric shapes.
- Kites in Tiling: Kites are used in creating complex tiling patterns, such as Penrose tilings. These tilings have applications in art, architecture, and understanding quasicrystals in materials science.
- Area Calculation Using Trigonometry: For advanced calculations, the area of a kite can also be derived using trigonometric functions if the lengths of the sides and the angles between them are known.
- Special Types of Kites: Rhombuses and squares are special cases of kites where all sides are equal. Understanding these relationships helps in recognizing kites within other geometric shapes and solving related problems.
- Kites in Coordinate Geometry: By placing a kite in the coordinate plane, one can use algebraic methods to determine properties such as the slopes of the diagonals, the coordinates of intersection points, and the lengths of sides.
These advanced topics provide a richer understanding of kites and their applications in various fields. By exploring these areas, students and researchers can develop more comprehensive skills in geometry and related disciplines.
Practice Problems
Here are some practice problems to help you understand how to calculate the perimeter of a kite. Use the formula \( P = 2(a + b) \) where \( a \) and \( b \) are the lengths of the two pairs of adjacent sides.
Problem 1
Given a kite with side lengths \( a = 5 \, \text{cm} \) and \( b = 7 \, \text{cm} \), calculate the perimeter.
- Identify the lengths of the sides: \( a = 5 \, \text{cm} \), \( b = 7 \, \text{cm} \).
- Apply the formula: \( P = 2(a + b) \).
- Calculate the perimeter: \( P = 2(5 + 7) = 2 \times 12 = 24 \, \text{cm} \).
Answer: 24 cm
Problem 2
A kite has side lengths of \( a = 8 \, \text{m} \) and \( b = 10 \, \text{m} \). Find the perimeter.
- Identify the side lengths: \( a = 8 \, \text{m} \), \( b = 10 \, \text{m} \).
- Apply the formula: \( P = 2(a + b) \).
- Calculate the perimeter: \( P = 2(8 + 10) = 2 \times 18 = 36 \, \text{m} \).
Answer: 36 m
Problem 3
Find the perimeter of a kite with sides \( a = 4.5 \, \text{cm} \) and \( b = 6.5 \, \text{cm} \).
- Identify the side lengths: \( a = 4.5 \, \text{cm} \), \( b = 6.5 \, \text{cm} \).
- Apply the formula: \( P = 2(a + b) \).
- Calculate the perimeter: \( P = 2(4.5 + 6.5) = 2 \times 11 = 22 \, \text{cm} \).
Answer: 22 cm
Problem 4
If a kite has side lengths \( a = 12 \, \text{in} \) and \( b = 15 \, \text{in} \), what is the perimeter?
- Identify the side lengths: \( a = 12 \, \text{in} \), \( b = 15 \, \text{in} \).
- Apply the formula: \( P = 2(a + b) \).
- Calculate the perimeter: \( P = 2(12 + 15) = 2 \times 27 = 54 \, \text{in} \).
Answer: 54 in
Problem 5
Determine the perimeter of a kite with sides \( a = 3 \, \text{m} \) and \( b = 4 \, \text{m} \).
- Identify the side lengths: \( a = 3 \, \text{m} \), \( b = 4 \, \text{m} \).
- Apply the formula: \( P = 2(a + b) \).
- Calculate the perimeter: \( P = 2(3 + 4) = 2 \times 7 = 14 \, \text{m} \).
Answer: 14 m
Summary and Key Takeaways
The perimeter of a kite is an essential geometric property that can be easily calculated using a simple formula. Here are the key points to remember:
- The perimeter of a kite is the total distance around its edges.
- A kite has two pairs of adjacent sides that are equal in length.
- The formula for calculating the perimeter of a kite is given by:
- Here, \( a \) and \( b \) are the lengths of the two pairs of equal sides of the kite.
- To find the perimeter, simply add the lengths of one pair of sides to the lengths of the other pair, then multiply the sum by 2.
- This formula ensures a quick and accurate calculation of the kite's perimeter.
\[
\text{Perimeter} = 2(a + b)
\]
Let's consider a few examples to illustrate this:
- Example 1: A kite with side lengths of 12 inches and 15 inches has a perimeter calculated as follows:
\[
\text{Perimeter} = 2(12 + 15) = 2(27) = 54 \text{ inches}
\] - Example 2: A kite with sides in the ratio of 3:5, and the smaller side being 24 inches, has a perimeter:
\[
\text{Given: } a = 24 \text{ inches, } \text{ ratio } a:b = 3:5 \Rightarrow b = 24 \times \frac{5}{3} = 40 \text{ inches}
\]
\[
\text{Perimeter} = 2(24 + 40) = 2(64) = 128 \text{ inches}
\] - Example 3: A kite with side lengths of 20 cm and 35 cm has a perimeter:
\[
\text{Perimeter} = 2(20 + 35) = 2(55) = 110 \text{ cm}
\]
By understanding and applying these principles, calculating the perimeter of a kite becomes straightforward. These fundamental concepts can also be extended to solve various geometric problems involving kites in both academic and real-life applications.
Frequently Asked Questions
-
What is the perimeter of a kite?
The perimeter of a kite is the total distance around its edges. It can be calculated by adding the lengths of all its sides. The formula for the perimeter of a kite is:
\[ P = 2(a + b) \]where \(a\) and \(b\) are the lengths of the two pairs of adjacent sides.
-
How do you calculate the perimeter of kite WXYZ?
To calculate the perimeter of kite WXYZ, measure the lengths of its two pairs of adjacent sides. Suppose the lengths are \(a\) and \(b\), then use the formula:
\[ P = 2(a + b) \]For example, if one pair of sides is 10 cm and the other pair is 15 cm, the perimeter would be:
\[ P = 2(10 + 15) = 2 \times 25 = 50 \, \text{cm} \] -
What is the angle between the diagonals of a kite?
The diagonals of a kite are perpendicular to each other. Thus, they intersect at a right angle (90°).
-
Is a kite a quadrilateral?
Yes, a kite is a type of quadrilateral. It has two pairs of adjacent sides that are of equal length.
-
Can the perimeter of a kite be calculated if only the diagonals are known?
No, the perimeter of a kite cannot be directly calculated from the diagonals alone. The lengths of the sides are required to determine the perimeter.
Hướng dẫn tính chu vi và diện tích của hình thoi, hình thang và hình diều bằng tiếng Việt. Video giải thích chi tiết và dễ hiểu để thu hút người xem.
Chu vi và Diện tích của Hình thoi, Hình thang và Hình diều
READ MORE:
Video giải thích các thuộc tính của hình diều bằng tiếng Việt. Nội dung chi tiết và dễ hiểu giúp người xem nắm bắt các khái niệm cơ bản về hình diều trong hình học.
Các thuộc tính của Hình diều